J. Cent. South Univ. (2017) 24: 2154-2163
DOI: https://doi.org/10.1007/s11771-017-3624-4
Limit equilibrium analysis for rock slope stability using basic Hoek–Brown strength criterion
DENG Dong-ping(邓东平), ZHAO Lian-heng(赵炼恒), LI Liang(李亮)
School of Civil Engineering, Central South University, Changsha 410075, China
 Central South University Press and Springer-Verlag GmbH Germany 2017
Central South University Press and Springer-Verlag GmbH Germany 2017
Abstract:
Hoek–Brown (HB) strength criterion can reflect rock’s inherent failure nature, so it is more suitable for analyzing the stability of rock slopes. However, the traditional limit equilibrium methods are at present only suitable for analyzing the rock slope stability using the linear equivalent Mohr–Coulomb (EMC) strength parameters instead of the nonlinear HB strength criterion. Therefore, a new method derived to analyze directly the rock slope stability using the nonlinear HB strength criterion for arbitrary curve slip surface was described in the limit equilibrium framework. The current method was established based on certain assumptions concerning the stresses on the slip surface through amending the initial normal stress σ0 obtained without considering the effect of inter-slice forces, and it can satisfy all static equilibrium conditions of the sliding body, so the current method can obtain the reasonable and strict factor of safety (FOS) solutions. Compared with the results of other methods in some examples, the feasibility of the current method was verified. Meanwhile, the parametric analysis shows that the slope angle β has an important influence on the difference of the results obtained using the nonlinear HB strength criterion and its linear EMC strength parameters. For β≤45°, both of the results are similar, showing the traditional limit equilibrium methods using the linear EMC strength parameters and the current method are all suitable to analyze rock slope stability, but for β>60°, the differences of both the results are obvious, showing the actual slope stability state can not be reflected in the traditional limit equilibrium methods, and then the current method should be used.
Key words:
1 Introduction
Slope stability analysis is an important aspect of geotechnical engineering research, and it has attracted a lot of attentions from scholars in recent years with the growth in infrastructure construction and the frequency of natural disasters [1-4]. Previous research on slope stability analysis has focused mainly on the following two aspects: 1) calculation methods, and 2) strength criterions that describe the shear failure behavior of geotechnical materials. The calculation methods that have been developed to analyze slope stability include limit equilibrium method (LEM) [5-7], limit analysis method (LAM) [8-10], and numerical simulation method (NSM) [11-13]. Among these calculation methods, LEM have been the most widely applied in engineering practice, as they employ some simple formulas to calculate the slope factor of safety (FOS), based on the appropriate assumptions concerning inter-slice forces and the static equilibrium conditions of the sliding body. In the failure criterions that have been defined, the linear Mohr–Coulomb (MC) strength criterion [14, 15] includes only two strength parameters, i.e., cohesion c and internal friction angle φ, so it is often and easily used to describe the shear failure behavior of geotechnical materials. All types of calculation methods have been also applied to the MC strength criterion to analyze slope stability. However, according to experimental and engineering data, the shear failure behavior of some geotechnical materials exhibits nonlinear features, so it is inappropriate to employ the MC strength criterion in analyzing the stability of slopes composed of such materials. Particularly, the MC strength criterion also cannot explain the effect of a low stress zone in rock. To better show the shear failure behavior of rock, HOEK et al [16, 17] developed nonlinear Hoek–Brown (HB) strength criterion after studying a large amount of experimental data from field tests conducted on rocks. At present, the HB strength criterion can reflect rock’s inherent nature and the effects of some particular factors on the strength of a rock mass,including the strength of rock, number of structural planes, and stress state, and it has been an essential criterion to study the deformation and failure characteristics of rock slopes. Due to more and more landslide of rock slopes occur, the stability analysis of rock slopes using the HB strength criterion [18-20] has also yielded considerable interest in the international engineering geology community.
Actually, for most of traditional LEM, it is difficult to apply directly the HB strength criterion to derive the calculation formulas of slope FOS, as a result of the complexity of the criterion expression formula. Therefore, the linear equivalent MC (EMC) strength paramters, proposed by HOEK et al [21], is used instead of the nonlinear HB strength criterion to study rock slope stability [22, 23]. In the equivalence calculation process, the shear strength parameters of the MC strength criterion are obtained based on the principle that the area covered by the curves of the two criterions is the same in the σ (normal stress) - τf (shear strength) axes coordinate system. Therefore, in the linear EMC strength criterion, the effect of actual shear strength of the slip surface on slope stability is neglected, because that for one zone of the normal stresses, the shear strength calculated using the linear EMC strength parameters may be larger or smaller than that calculated using the nonlinear HB strength criterion, so it is important that a new LEM is established to analyze directly the rock slopes stability using the nonlinear HB strength criterion.
In this work, a new method is proposed for rock slope stability analysis that combines the LEM with a simplified form of the HB strength criterion, derived using a Taylor series expansion. The current method is established based on certain assumptions concerning the stresses on the slip surface, and once the stresses on the slip surface are solved according to the equilibrium conditions of the sliding body, the slope FOS can also be determined. Through comparing the current method with traditional LEM using the linear EMC strength parameters, including the Swedish method, simplified Bishop method, Spencer method and Morgenstern-Price (M–P) method, the feasibility of the current method was verified. Meanwhile, the differences between the results obtained with the current method and those obtained with traditional LEM using the linear EMC strength parameters were analyzed.
2 HB strength criterion and its linear EMC strength parameters
2.1 HB strength criterion
The HB strength criterion is used to obtain strength of the joint geotechnical body, and assess the interaction degree and conditions of the contact surface between the rock mass, so this criterion is very suitable to apply to evaluating the rock slope stability. In the HB strength criterion, it can be expressed using the instantaneous cohesion (ci) and internal friction angle (φi), which have the same meaning with strength parameters of the MC strength criterion, and HOEK [24] obtained their formulas according to the combination of experimental studies and theoretical analysis. Based on the formulas of instantaneous cohesion and internal friction angle, HOEK [24] gave the calculation of the shear strength τf in a given normal stress σ as
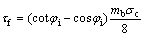 (1)
(1)
where φi is the instantaneous friction angle and can be calculated from Eq. (2); mb is a material constant, related to the intact material constant mi, which reflects the hardness of the rock and ranges between 0.001 and 25.0; and σc is the uniaxial compressive strength.
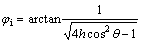 (2)
(2)
where
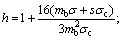 s is a parameter that reflects the degree of fragmentation of the rock and ranges between 0.0 and 1.0; and σ is the normal stress.
s is a parameter that reflects the degree of fragmentation of the rock and ranges between 0.0 and 1.0; and σ is the normal stress.
Using the parameter of geological strength index (GSI, Igs), mb and s can be expressed as
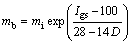 (3a)
(3a)
 (3b)
(3b)
where D is a rock weakening factor related to the excavation mode and degree of disturbance of the rock mass, and it ranges between 0 and 1 with 0 representing an unperturbed state.
2.2 Linear EMC strength parameters of HB strength criterion
Equation (1) shows the calculation of shear strength in the HB strength criterion, due to the complexity of Eq. (1), it is difficult to derive the general expression for calculating directly the FOS for rock slope stability analysis with the HB strength criterion. Therefore, in order to apply the HB strength criterion to the rock slope stability analysis, the previous researchers established the linear EMC strength parameters instead of the nonlinear HB strength criterion to achieve this purpose using the existing methods. For example, to obtain the linear EMC strength parameters of the HB strength criterion, HOEK et al [21] firstly established σ and τf axes coordinate system, and then defined the tensile strength σt and limit of the corresponding maximum confining pressure σ3max. When the tensile stress ranges between σt and σ3max, curve of the HB strength criterion is fitted adopting the MC strength parameters. The principle of optimal fitting is that the areas covered by the curves corresponding to two criterions within this specific range of σt and σ3max are the same. According to this principle, the calculation for the linear EMC strength parameters, i.e., cohesion c and the internal friction angle φ, are given by HOEK et al [21] as:
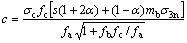 (4a)
(4a)
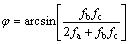 (4b)
(4b)
where α is a coefficient that reflects the characteristics of the rock mass, and it can also be expressed as a function of GSI, i.e., σc, mb and s have the same meaning with Eq. (1); and σ3n is a parameter calculated by Eq. (5).
σc, mb and s have the same meaning with Eq. (1); and σ3n is a parameter calculated by Eq. (5).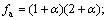 fb=6αmb; and
fb=6αmb; and 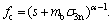
In Eq. (4), α should have the value of 0.5 to make the MC strength parameters from Eqs. (4a) and (4b) be equivalent with the HB strength criterion, as given in Eq. (1). When α=0.5, the relationship between α and GSI is utilized to obtain that Igs=100. In addition, σ3n for Eq. (4) can be calculated as
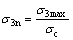 (5)
(5)
where σ3max is the limit of maximum confining pressure, and the relationship between σ3max and rock mass strength σcm can be described as
 (6)
(6)
where k and m are empirical parameters, k=0.72 and m= -0.91 in slope engineering; γ is the unit weight of rock mass; H is the slope height; and σcm is the rock mass strength with its formulas given as
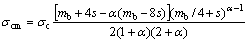 (7)
(7)
3 LEM for rock slope stability analysis using HB strength criterion
3.1 Assumption of stresses on slip surface
As shown in Fig. 1, the xy axes coordinate system is established with its origin at the slope toe. A and B are the lower and upper sliding points of slip surface, respectively; g(x) and s(x) are the equations for the slope outline and slip surface, respectively. The micro-unit slice a1b1c1d1 with width dx is selected to analyze the forces. Under typical conditions, the forces acting on the micro-unit slice a1b1c1d1 are as follows: wdx is the weight force; kHwdx and kVwdx are the seismic force in the horizontal and vertical direction, respectively, where kH and kV are the horizontal and vertical seismic coefficient, respectively; qxdx and qydx are the external load on the slope in the horizontal and vertical direction, respectively; σdx/cosδ and τdx/cosδ are the normal and shear force on the slip surface, respectively, where δ is the horizontal inclination angle of the tangent to the slip surface.
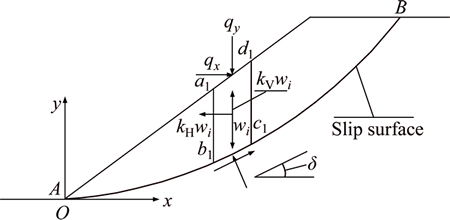
Fig. 1 Stress analysis of micro-unit slice
Ignoring the inter-slice forces illustrated in Fig. 1, the force equilibrium conditions on the micro-unit slice a1b1c1d1 in x- and y-axis direction are given as
 (8a)
(8a)
 (8b)
(8b)
where σ0 and τ0 are the normal and shear stresses on the slip surface without considering the effect of inter-slice forces, respectively; s′ is the first derivative of slip surface equation s(x) with respect to the x-axis, and s′=tanδ.
By solving Eq. (8), the normal stress σ0 can be obtained as
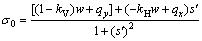 (9)
(9)
However, as a result of the existence of inter-slice forces, there is a difference between σ0 obtained from Eq. (10) and actual normal stress. Therefore, in order to obtain the result of σ that is closer to the actual normal stress, σ0 is amended as
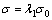 (10)
(10)
where λ1 is a variable and σ is the normal stress on slip surface.
In the slope stability analysis, FOS (Fs) is generally defined as the ratio of failure shear force to the actual shear force on slip surface, i.e., Fs=(τfdx)/(τdx) in the micro-unit slice. Rearranging the above expression, it can be obtained that τ=τf/Fs. Then, based on Eq. (1), the shear stress τ on slip surface is expressed as
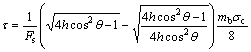 (11)
(11)
Equation (11) indicates that the shear stress τ is a function of the normal stress σ. According to Eq. (12), the first derivative of shear stress τ with respect to the normal stress σ can be obtained as
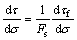 (12)
(12)
where 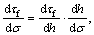 and
and 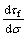 is equivalent to tanφi, i.e., the tangent of aforementioned instantaneous internal friction angle in the HB strength criterion;
is equivalent to tanφi, i.e., the tangent of aforementioned instantaneous internal friction angle in the HB strength criterion; 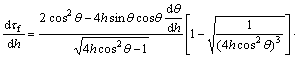
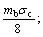
 and
and 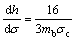 .
.
Using Taylor series expansion with the normal stress σ0 as initial value in Eq. (11) and substituting Eqs. (11) and (13), Eq. (11) can be re-expressed as
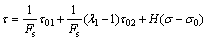 (13a)
(13a)
 (13b)
(13b)

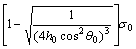 (13c)
(13c)
where 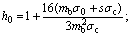
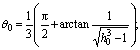 and H(σ–σ0) is the higher-order error term.
and H(σ–σ0) is the higher-order error term.
When the initial stress σ0 is similar to σ, i.e., λ1 tends to unity in Eq. (10), H(σ–σ0) in Eq. (13a) contributes little to the shear stress τ. In fact, σ0 is the approximate solution of σ, so H(σ–σ0) can be neglected. Then, applying two variables, i.e., λ2 and λ3, to amend τ01 and τ02 in Eq. (13), respectively, the shear stress τ is calculated as
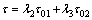 (14)
(14)
In Eq. (14), the variables λ2 and λ3 also include the effect of H(σ–σ0) on the shear stress τ.
As shown in Fig. 1, the force equilibrium conditions in x- and y-axis direction and the moment equilibrium condition of all forces about one point (xc, yc) in the sliding body can be determined as
 (15a)
(15a)
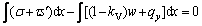 (15b)
(15b)
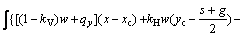
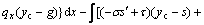
 (15c)
(15c)
Substituting Eqs. (15a-b) into Eq. (15c) and simplifying, the following formula can be obtained as

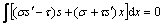 (16)
(16)
Then, substituting Eqs. (10) and (14) into Eqs. (15a-b), and (16), the following linear equations for variables λ1, λ2, and λ3 can be obtained as
 i =1, 2, 3 (17)
i =1, 2, 3 (17)
where aij and bi are the calculation parameters, and their formulas are given in Table 1.
Table 1 Calculation parameters for slope stability

After these variables λ1, λ2, and λ3 are solved by using Eq. (17), the normal stress σ and shear stress τ can then be obtained by substituting them into Eqs. (10) and (14).
3.2 Calculation for slope FOS
According to the aforementioned definition of slope FOS, i.e., the ratio of the failure shear force to the actual shear force on slip surface, the slope FOS (Fs) with the HB strength criterion can be calculated as
 (18)
(18)
where φi, mb and σc have the same meaning with Eq. (1); σ can be calculated using Eq. (10); and τ can be calculated using Eq.(14).
4 Slope examples
4.1 Comparison analysis on rock slope stability
Slope example 1: as illustrated in Fig. 2, the rock slope height H=20 m, slope angle β=45°, and the rock destruction is subject to the HB strength criterion with the following parameters as: γ=23.0 kN/m3, D=0, Igs= 100, α=0.5, mi=10, and σc=0.4γH. The xy axes coordinate system is established with the origin at slope toe. A (A1 or A2) and B (B1 or B2) are the lower and upper sliding points of the slip surface, respectively.

Fig. 2 Sketch of slope examples:
According to the above analysis, the rock slope stability is analyzed using the traditional LEM with the linear EMC strength parameters instead of the HB strength criterion. Actually, if this problem can be directly solved with the nonlinear HB strength criterion, the obtained results would be more satisfying with the actual needs. In this work, to assess the differences of the calculation methods under two criterions, the traditional LEM, i.e., the Swedish method (named by the Swedish method 1), simplified Bishop method, Spencer method, and M–P method, are adopted using the linear EMC strength parameters. Meanwhile, among these traditional LEM, the Swedish method neglects the effect of inter-slice forces, so it can easily be used to analyze slope stability using the nonlinear HB strength criterion, named by Swedish method 2.
In addition, the equivalence of MC strength parameters for the HB strength criterion relates to the normal stresses on slip surface, so two types of slip surfaces at the specific positions, i.e., circular and arbitrary curve, were also considered. The arbitrary curve slip surface, proposed by DENG et al [25], consists of a fold line with n segments.
For case 1, the deep slip surfaces are shown in Fig. 2(a), the coordinates of points A1 and B1 are (0 m, 0 m) and (30 m, 20 m), respectively, the arc radius of circular slip surface R = 30m, and the parameters of arbitrary curve slip surface at a specific position are given as: n=100, δ1=0°, and 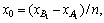 where δ1 is the horizontal inclination angle of first segment of the fold line, and it is positive in the clockwise direction, x0 is the width of first segment of the fold line.
where δ1 is the horizontal inclination angle of first segment of the fold line, and it is positive in the clockwise direction, x0 is the width of first segment of the fold line.
For case 2, the shallow slip surfaces are shown in Fig. 2(b), the coordinates of points A2 and B2 are (0 m,0 m) and (22 m, 20 m), respectively, the arc radius of circular slip surface R = 35 m, and the parameters of arbitrary curve slip surface are given as: n=100, δ1=-20°, and 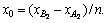
In the two cases described above, the results of the Swedish method 1, Swedish method 2, simplified Bishop method, Spencer method, M–P method, and the current method are listed in Table 2, the normal stresses on the circular slip surface are shown in Fig. 3, and that on the arbitrary curve slip surface are shown in Fig. 4. In Figs. 3-4, it should be noted that if the normal stress σ is located in zone 1, i.e., 0<σ<σ1, the shear strength of the EMC criterion is bigger than that of the HB strength criterion, but if the normal stress σ is located in zone 2, i.e., σ1<σ<σ2, the difference on both of the shear strengths is very small. Therefore, compared with the calculation methods with the linear EMC strength parameters, the current method analyzes the effect of actual shear strength on slope stability to solve more accurate FOS.
Table 2 and Figs. 3-4 show that: 1) For the deep slip surface of case 1, most of the normal stresses on slip surface are located in zone 2, so both of the results calculated using the EMC strength parameters and nonlinear HB strength criterion are similar. However, for the shallow slip surface of case 2, most of the normal stresses are located in zone 1, so the results of the linear EMC strength criterion are bigger than those of the nonlinear HB strength criterion. Therefore, the position of slip surface has an important influence on both of the results obtained using the two criterions; 2) Compared with the Swedish method 2, the current method can satisfy all static equilibrium conditions and amend the initial stress σ0 obtained without considering the effect of inter-slice forces, so the results of the current method are greater and more reasonable, and it is also suitable for the arbitrary curve slip surface; 3) In the traditional LEM, such as the simplified Bishop method, Spencer method, and M–P method, the effect of inter-slice forces is considered so as to not obtain easily the explicit expressions for stresses on the slip surface. Thus, it is difficult to analyze directly rock slope stability using the traditional LEM with the nonlinear HB strength criterion. However, the current method solved this problem.
Table 2 Contrast on calculated results for slope stability with specific slip surfaces
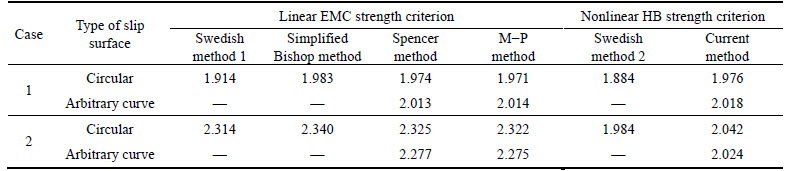

Fig. 3 Contrast on normal stress of circular slip surface at specific position:(1—Curve of nonlinear HB strength criterion; 2—Curve of linear EMC strength criterion; 3—Deep slip surface in case 1; 4—Normal stress on slip surface in case 1; 5—Shallow slip surface in case 2; 6—Normal stress on slip surface in case 2)

Fig. 4 Contrast on normal stress of arbitrary curve slip surface at specific position:(1—Curve of nonlinear HB strength criterion; 2—Curve of linear EMC strength criterion; 3—Deep slip surface in case 1; 4—Normal stress on slip surface in case 1; 5—Shallow slip surface in case 2; 6—Normal stress on slip surface in case 2)
Slope example 2: the rock slope is described by LI et al [26] with slope height H=25 m, and the rock destruction is subject to the HB strength criterion with the following parameters as: γ=23 kN/m3, D=0, Igs=100 and α=0.5. With the slope FOS of being unity, LI et al [26] calculated various combinations of the slope height β, mi, and dimensionless parameter σc/(γH) using the limit analysis lower bound method with the nonlinear HB strength criterion, and these parameters are listed in Table 3. To verify the feasibility of the current method proposed in this work, the results of the Swedish method 1, Swedish method 2, Simplified Bishop method, Spencer method, M–P method and the current method are calculated using the parameters given by LI et al [26] and assuming a circular slip surface. The results are also summarized in Table 3.
Table 3 shows that 1) both of the results obtained using limit analysis lower bound method and the current method differ by less than 1%, indicting the feasibility of the current method. However, compared with limit analysis lower bound method, the results of other methods using the linear EMC strength parameters are all more than 10% greater; 2) compared with Swedish method 2, the current method also has larger and more reasonable results.
4.2 Parametric analysis
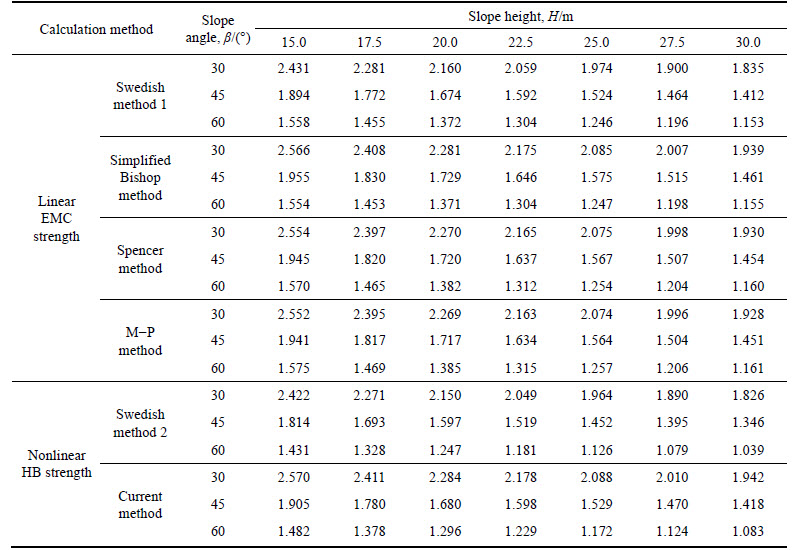
According to the above analysis, the feasibility of the current method is verified, and the research indicates that the position of slip surface has an important effect on the difference of the results calculated using the nonlinear HB strength criterion and its linear EMC strength parameters. Therefore, we select two main factors on the position of slip surface, i.e., slope height and slope angle, to conduct parametric analysis, and the applicability of the linear EMC strength parameters is also studied. The rock is subject to the HB strength criterion with the parameters as: γ=23.0 kN/m3, D=0,Igs=100, α=0.5, mi=10, and σc=0.14 MPa. When the rock slope height H is 15.0, 17.5, 20.0, 22.5, 25.0, 27.5 and 30.0 m, respectively, and slope angle β is 30°, 45°, and 60°, respectively, the minimum slopes FOS of different methods are listed in Table 4, and the differences between the current method and other methods are shown in Fig. 5. In Fig. 5, the Simplified Bishop method, Spencer method, and M–P method yield similar results, also the maximum and minimum differences between the current method and the three methods are given.
Table 4 and Fig. 5 show that: 1) the slope height H has little influence on the differences of the results obtained using the nonlinear HB strength criterion and its linear EMC strength parameters, but the slope angle β, relating with the position of slip surface, has an important effect; 2) When β≤45°, the differences of the results obtained using the nonlinear HB strength criterion and its linear EMC strength parameters are less than 4%, whereas when β≥60°, both of the results obtained using the two criterions differ by more than 5%.
Table 3 Contrast on results of calculation methods with nonlinear HB strength criterion and its linear EMC strength parameters
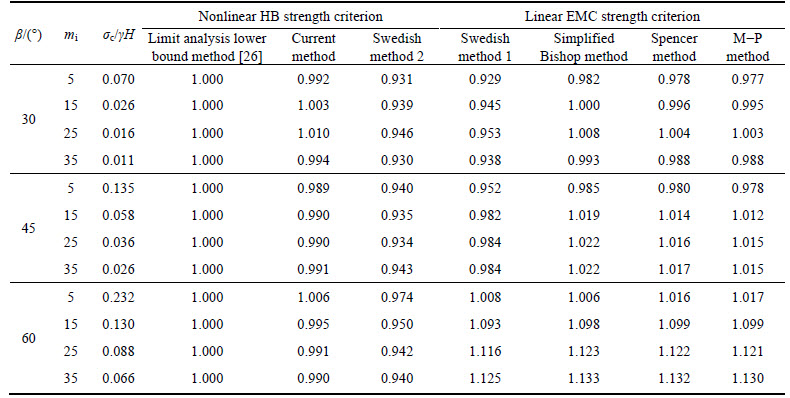
Table 4 Contrast on minimum FOS with different slope height and slope angle
Based on the analysis discussed above, we can obtain that if β≤45°, the traditional LEM using the linear EMC strength parameters are suitable for use in analyzing rock slope stability. However, if β>60°, the current method should be used to get more accurate results instead of the traditional LEM using the linear EMC strength parameters.
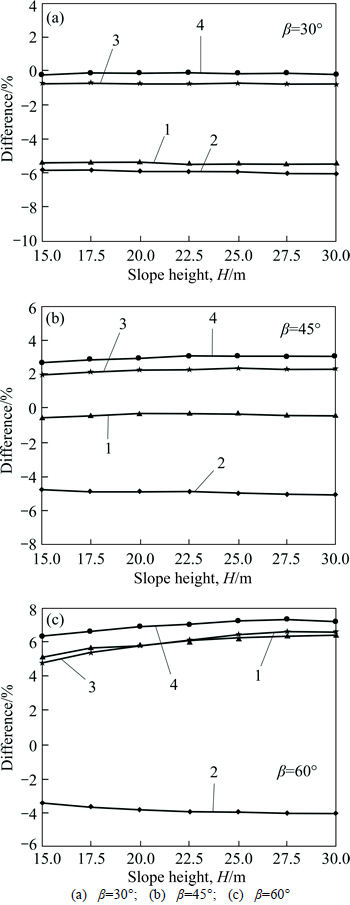
Fig. 5 Difference between current method and traditional LEM:(1—
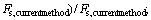 2—
2—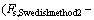
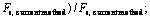 3—
3—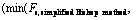
 4—
4—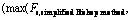


5 Conclusions
A new method for limit equilibrium analysis of rock slope stability using the nonlinear HB strength criterion is proposed on the basis of certain assumptions concerning the stress on slip surface. By analyzing some slope examples, the feasibility of the current method is verified, and the following conclusions can be drawn.
1) Compared with the Swedish method with the nonlinear HB strength criterion, the current method satisfies all limit equilibrium conditions of the sliding body and amends the initial normal stress without considering the effect of inter-slice forces, so it can yield stricter and more reasonable results.
2) The position of slip surface has important effect on differences of the results obtained using the nonlinear HB strength criterion and its linear EMC strength parameters, and the slope angle is one main factor relating with the position of the critical slip surface.
3) For the slope angle β≤45°, the current method and the traditional LEM using the linear EMC strength parameters are both suitable for use in analyzing rock slope stability. However, if β>60°, the current method should be used to get more accurate FOS solutions.
References
[1] KULATILAKE P H S W, WANG L Q, TANG H M, LIANG Y. Evaluation of rock slope stability for Yujian River dam site by kinematic and block theory analyses [J]. Computers and Geotechnics, 2011, 38(6): 846-860.
[2] ZHOU X P, CHENG H. Analysis of stability of three-dimensional slopes using the rigorous limit equilibrium method [J]. Engineering Geology, 2013, 160(12): 21-33.
[3] MORADI A A, OSANLOO M. Determination and stability analysis of ultimate open-pit slope under geomechanical uncertainty [J]. International Journal of Mining Science and Technology, 2014, 24(1): 105-110.
[4] MOHTARAMI E, JAFARI A, AMINI M. Stability analysis of slopes against combined circular-toppling failure [J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 67(4): 43-56.
[5] BISHOP A W. The use of the slip circle in the stability analysis of earth slopes [J]. Géotechnique, 1955, 5(1): 7-17.
[6] SPENCER E. A method of analysis of the stability of embankments assuming parallel inter-slice forces [J]. Geotechnique, 1967, 17(1): 11-26.
[7] MORGENSTERN, PRICE V E. The analysis of the stability of general slip surfaces [J]. Geotechnique, 1965, 15(1): 79-93.
[8] LI A J, LYAMIN A V, MERIFIELD R S. Seismic rock slope stability charts based on limit analysis methods [J]. Computers and Geotechnics, 2009, 36(1): 135-148.
[9] ZHAO L H, LI L, YANG F, LUO Q, LIU X. Upper bound analysis of slope stability with nonlinear failure criterion based on strength reduction technique [J]. Journal of Central South University of Technology, 2010, 17(4): 836-844.
[10] YANG X G, CHI S C. Upper bound finite element analysis of slope stability using a nonlinear failure criterion [J]. Computers and Geotechnics, 2013, 54(10): 185-191.
[11] LI L C, TANG C A, ZHU W C, LIANG Z Z. Numerical analysis of slope stability based on the gravity increase method [J]. Computers and Geotechnics, 2009, 36(7): 1246-1258.
[12] MEHDIPOURA I, GHAZAVIB M, MOAYED R Z. Numerical study on stability analysis of geocell reinforced slopes by considering the bending effect [J]. Geotextiles and Geomembranes, 2013, 37(4): 23-24.
[13] ZHANG Z, HAN J, YE G B. Numerical investigation on factors for deep-seated slope stability of stone column-supported embankments over soft clay [J]. Engineering Geology, 2014, 168(2): 104-113.
[14] CHENG Y M, LANSIVAARA T, BAKER R, LI N. Use of internal and external variables and extremum principle in limit equilibrium formulations with application to bearing capacity and slope stability problems [J]. Soils and Foundations, 2013, 53(1): 130-143.
[15] HUANG C C. Developing a new slice method for slope displacement analyses [J]. Engineering Geology, 2013, 157(8): 39-47.
[16] HOEK E, BROWN E T. Empirical strength criterion for rock masses [J]. Journal of Geotechnical and Geoenvironmental Engineering, 1980, 106(9): 1013-1035.
[17] HOEK E, BROWN E T. Practical estimates of rock mass strength [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165-1186.
[18] SHEN J Y, KARAKUS M, XU C S. Chart-based slope stability assessment using the generalized Hoek-Brown criterion [J]. International Journal of Rock mechanics and Mining Sciences, 2013, 64(6): 210-219.
[19] FU W X, LIAO Y. Non-linear shear strength reduction technique in slope stability calculation [J]. Computers and Geotechnics, 2010, 37(3): 288-298.
[20] NEKOUEI A M, AHANGARI K. Validation of Hoek-Brown failure criterion charts for rock slopes [J]. International Journal of Mining Science and Technology, 2013, 23(6): 805-808.
[21] HOEK E, CARRANZA T C, CORKUM B. Hoek-Brown failure criterion—2002 edition [C]// Proceedings of the North American Rock Mechanics Society NARMS-TAC 2002. Toronto: University of Toronto Press, 2002: 267-273.
[22] LI A J, CASSIDY M J, WANG J, MERIFIELD R S, LYAMIN A V. Parametric Monte Carlo studies of rock slopes based on the Hoek-Brown failure criterion [J]. Computers and Geotechnics, 2012, 45(12): 11-18.
[23] LI W Y, WU Q H. Factor of safety of slope based on nonlinear Hoek-Brown limit equilibrium method [J]. Journal of Central South University: Science and Technology, 2013, 44(6): 2537-2542. (in Chinese)
[24] HOEK E. Estimating Mohr-Coulomb friction and cohesion values from the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1990, 27(3): 227-229.
[25] DENG D P, LI L, ZHAO L H. A new method of sliding surface searching for general stability of slope based on Janbu method [J]. Rock and Soil Mechanics, 2011, 32(3): 891-898. (in Chinese)
[26] LI A J, MERIFIELD R S, LYAMIN A V. Stability charts for rock slopes based on the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(5): 689-700.
(Edited by FANG Jing-hua)
Cite this article as:
DENG Dong-ping, ZHAO Lian-heng, LI Liang. Limit equilibrium analysis for rock slope stability using the Basic H–B strength criterion [J]. Journal of Central South University, 2017, 24(9): 2154–2163.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-017-3624-4Foundation item: Project(2015M580702) supported by China Postdoctoral Science Foundation; Project(51608541) supported by the National Natural Science Foundation of China; Project(2014122066) supported by the Guizhou Provincial Department of Transportation Foundation, China
Received date: 2015-09-20; Accepted date: 2016-03-22
Corresponding author: DENG Dong-ping, PhD; Tel: +86-13975150476; E-mail: dengdp851112@126.com
Abstract: Hoek–Brown (HB) strength criterion can reflect rock’s inherent failure nature, so it is more suitable for analyzing the stability of rock slopes. However, the traditional limit equilibrium methods are at present only suitable for analyzing the rock slope stability using the linear equivalent Mohr–Coulomb (EMC) strength parameters instead of the nonlinear HB strength criterion. Therefore, a new method derived to analyze directly the rock slope stability using the nonlinear HB strength criterion for arbitrary curve slip surface was described in the limit equilibrium framework. The current method was established based on certain assumptions concerning the stresses on the slip surface through amending the initial normal stress σ0 obtained without considering the effect of inter-slice forces, and it can satisfy all static equilibrium conditions of the sliding body, so the current method can obtain the reasonable and strict factor of safety (FOS) solutions. Compared with the results of other methods in some examples, the feasibility of the current method was verified. Meanwhile, the parametric analysis shows that the slope angle β has an important influence on the difference of the results obtained using the nonlinear HB strength criterion and its linear EMC strength parameters. For β≤45°, both of the results are similar, showing the traditional limit equilibrium methods using the linear EMC strength parameters and the current method are all suitable to analyze rock slope stability, but for β>60°, the differences of both the results are obvious, showing the actual slope stability state can not be reflected in the traditional limit equilibrium methods, and then the current method should be used.


