J. Cent. South Univ. (2013) 20: 363–371

DOI: 10.1007/s11771-013-1496-9

Comparison of two types of twin-rotor piston engine mechanisms

DENG Hao(邓豪)¹, PAN Cun-yun(潘存云)¹, WANG Xiao-cong(王晓聪)², ZHANG Lei(张雷)¹ , DENG Li(邓力)¹

1. College of Mechatronic Engineering and Automation, National University of Defense Technology, Changsha 410073, China;

2. 63892 Unit, Luoyang 471000, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2013

Abstract:

A novel twin-rotor piston engine (TRPE) mechanism with high volumetric output and power density was introduced. This new engine comprises an energy conversion system and a differential velocity drive mechanism (DVDM). Two special geared four-bar mechanisms, DVDM-1 and DVDM-2, were utilized and compared. Based on the closed loop vector method, a mathematical model for position, velocity, and acceleration of the two mechanisms was established. Numerical examples illustrate that the kinematic characteristics were presented. Expression of the displacement and compression ratio of the two engine mechanisms were derived and compared. It is concluded that both DVDM-1 and DVDM-2 adopted in the proposed TRPE with six vane pistons create thirty-six power strokes per revolution of the output shaft, and the summation of two angles covered by each rocker is always 2p/N as the output shaft rotates an angle of p/N. In DVDM-1, the span angle of a vane piston should be designed to be 10.2°, and the compression ratio should be equal to 10; in DVDM-2, the span angle of a vane piston should be designed to be 10.6°, and the compression ratio should be equal to 4.3.

Key words:

rotor; piston engine; crank; rocker; power density；

1 Introduction

Many forms of engine mechanism have been contemplated and manufactured [1–4]. Most of them are used to reduce inherent disadvantages of conventional reciprocating piston engines [5–6]. For example, the SYTech engine based on the scotch yoke mechanism was developed by CMC Power Systems in Sydney, Australia [7]. The cardan gear mechanism was compared with the conventional slider-crank mechanism in air pumps and four-stroke engines [8]. Rotary piston engines [9–11] are claimed to possess many advantages over reciprocating engines such as having higher torque, fewer parts, lower mass and less reciprocating imbalance. However, for various reasons, Wankel rotary engine is the only one which achieves limited success despite of big efforts and funds, besides its sealing problems, long and narrow chambers causing poor combustion, and complex manufacture and repair haven’t been properly solved until now. So recently, more and more researchers reconsider designing other types of rotary engines. HUDSON [12] revealed his record of a lifetime of the parametric, mechanical design of a rotary engine. ERTESVAG [13] and ROY [14] reconsidered the sliding vane type engine.

On the other hand, under the demands of the future engine with efficiency and high power to mass ratio, variable compression ratio, and burning various kinds of fuels, the oscillatory rotating type engine [15], also named cat-and-mouse engine [16–17], has gained the most rapid development. The primary difference between the Wankel engine and the oscillatory rotating type engine is that while Wankel creates compression and expansion via the special shaping of the rotor, the oscillatory rotating engine as opposed to the relative motion of the circular rotors. LIBROVICH et al [18–19] proposed a novel rotary vane engine using non-circular gears for torque transmission. CHENG et al [20–21] studied the eccentric circular-noncircular gear driving system of differential velocity pump. LIANG [22] proposed a rotary engine with two rotors and its design method. CHUN [23] used the half rounded gear to alternately lock and unlock the rotors of his rotary engine. MORGADO [24] introduced an internal combustion engine and its design method. OMORI [25] provided a cat-and-mouse type internal combustion engine having a variable correlation type crank for a constant-pressure burning and a premixed compression ignition. WIESLAW [26] revealed a new conception of oscillating engine.

From researched studies, many proposals related to ratchet stops, cams, elliptical or half rounded gears are either unreliable or difficult to withstand excessive shocks. As we know, those shocks are inherent t in explosive engines. Besides, these proposals were resulted with cursory investigation and seldom-exposed mathematical model and analysis.

A novel oscillatory rotating engine, also named twin-rotor piston engine (TRPE) was introduced [27–28]. With advantages of high volumetric output and multiple power strokes per revolution of the output shaft, the TRPE has a compact and balanced design. Configuration and work principles of the TPRE were presented. The mathematical model of the TRPE for the position, velocity, and acceleration was established. Two types of TRPE mechanisms were introduced. The detailed analysis of two types of TRPE mechanisms was presented. Similarities and differences of the two mechanisms were identified and discussed. Expressions of the displacement and compression ratio of the two engine mechanisms were also derived and compared.

2 Configuration and working principle of trpe mechanism

The simple type of the TRPE is shown in Fig. 1 (a). Its basic mechanical structure, without considering the combustion system, cooling system, and lubricating system temporarily in this work, includes two major assemblies, an energy conversion system (ECS) and a differential velocity drive mechanism (DVDM).

ECS has two identical opposed rotors, the former rotor and the latter rotor. Both rotors are intersected mounted on the output shaft and enclosed in a stationary housing. In operation, the two rotors are driven by expanding ignited gas and rotate about a common axis of the output shaft in the same direction to convert heat energy into mechanical energy. The engine has 2N (N is a natural number) quadrant vane pistons in total, with each N vane pistons radiate attached to the rotor hub of each rotor.

In a preferred embodiment, as shown in Fig. 1 (b), each rotor has six vane pistons. The vane pistons on the former rotor are designated “Y₁” to “Y₆”, and the same on latter are designated “L₁” to “L₆”. Vane pistons extend the full width of the housing. The sealing of the high-pressured gas can be ensured by means of surface contact between the rotors and the housing. These twelve vane pistons divide the housing into twelve separated working chambers. Each of the working chamber, denoted by I–XII, is located between a vane piston on the former rotor and its adjacent vane piston on the latter rotor. Such that at any one time, one set of six working chambers is close together while the other set is wide apart. In addition, as one of the working chambers reaches its maximum volume, the adjacent two working chambers reach their minimum volume, and vice versa.

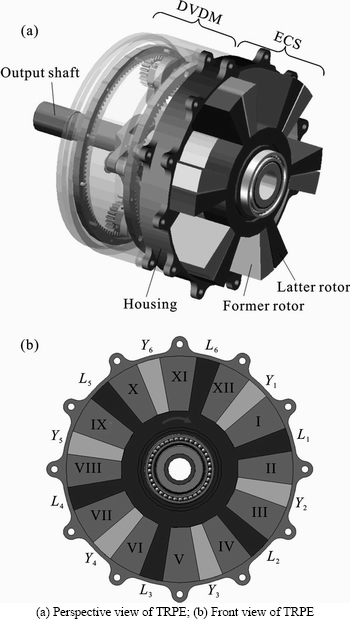
Fig. 1 Configuration of a TRPE (half part of housing omitted to show two rotors):

DVDM interconnects the two rotors and has them speed up and slow down by turns at certain time. As shown in Fig. 2, to generate the cyclically oscillatory rotation, DVDM-1 and DVDM-2, two specific geared four-bar mechanisms, are utilized in TRPE. Based on the crank-rocker and gear train technology, which has been well proven and perfected over hundreds years, the two types of DVDMs are inherently robust.

Each DVDM includes a stationary gear, two planetary gears, and two crank-rocker mechanisms (denoted by OABC and OA′B′C′ in Fig. 2). The two planetary gears mesh with the stationary gear for orbital motion. The two crank-rocker mechanisms are composed of a planet carrier (denoted by AA'), two cranks (denoted by AB and A'B'), two connecting rods (denoted by BC and B'C'), and two rockers (denoted by OC and OC'). The parameters of their respective components are the same.

The cranks are fixed on each respective planet gear, and positioned out of phase usually. As shown in Fig. 2, the phase (j) is 180°. The two rockers are respectively fixed to the two rotors by two separate hollow rotor shafts. The output shaft, which passes coaxially through the two hollow rotor shafts, is rigidly connected to the planet carrier. As the output shaft rotates, the two cranks, along with the planet gears are rotating in the same velocity. With a non-zero phase, the two cranks also restrain the two rockers (and the two rotors) to move in the same variable oscillatory rotation at a different pace. Thus, relative motion between rotors generates the volumetric change within each working chambers and creates the four-stroke cycle.

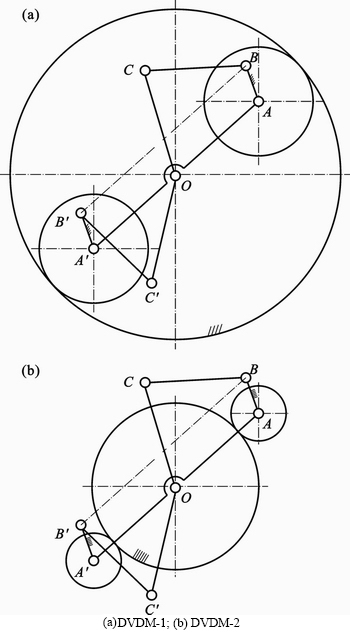
Fig. 2 Kinematical diagrams of two types of DVDM:

3 Mathematical model of two trpe mechanisms

3.1 Basic dimensions of TRPE mechanism

Based on the configuration mentioned in Fig. 2, the key technique is to duplicate the oscillatory motion of the rockers several times in one revolution of the output shaft. Thus, a cyclical symmetrical curve is first needed. As shown in Fig. 3, when the planet gears rotate outside the stationary gear, joints on the planet gears generate epicycloidal curves. Similarly, when the planet gears rotate inside the stationary gear, joints on the planet gears generate hypocycloidal curves.

For simplicity of comparison, the gear ratios of the two DVDM are presumed to be the same, and are defined as

                                   (1)

where r₁ and r₃ are the radii of the stationary gears, r₂ and r₄ are the radii of the planet gears.

Assuming that the gear carrier (OA) rotates an angle of q₁ in the counter-clockwise (CCW) direction, then the planet gear, (AB) in DVDM-1 rotates an angle of iq₁ in the same direction. Coordinates of the joint B on the planet gear, B_xe and B_ye, which trace an epicycloidal curve, are written as

              (2)

where l_OA is the distance from the center of the planet gear to the center of the stationary gear, l_AB is the distance from the center of the joint B to the center of the planet gear.

Similarly, coordinates of the joint B on the planet gear in DVDM-2, B_xh and B_yh, which trace a hypocycloidal curve, can also be written as

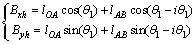              (3)

The shape of the curve is mostly determined by the parameter (i). i is the gear ratio, which can be expressed as

                                      (4)

where N>M, and both N and M are natural numbers and N can not be divided exactly by M.

Many curves can be applied as trajectories of joint B in the TRPE. N is the number of petals in cycloid curves. M, which is the revolution of the output shaft, is the number for forming an integrated cycloid curve. Figure 3 shows the two curves generated by the same gear ratio (=6). Shapes of the two curves are very different but both of the petals’ numbers are six.

In general, assuming that the gear ratio is N (M=1 for simplicity), the output shaft rotates one revolution, and then the two planet gears complete N revolutions. During this working process, the cranks on the planet gears restrain the two rockers to complete N oscillations and one revolution. In order to utilize the N oscillations and make sure all intake ports and exhaust ports be fixed at a certain position of the housing, the number of vane pistons on each rotors should be equal to gear ratio, i.e., .

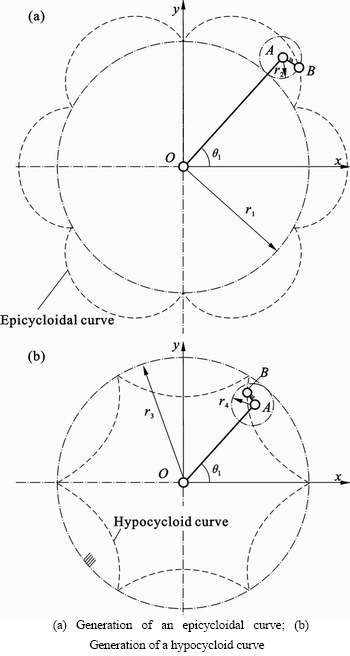
Fig. 3 Generation of epicycloidal and hypocycloid curves with six petals:

As one oscillation means one contraction and one expansion stroke for each working chamber, in one revolution of the output shaft, each of 2N working chambers completes N/2 power strokes. Thus, the number of power strokes per revolution of the output shaft, C, can be expressed as

C=N²                                       (5)

The same stroke is performed simultaneously in N/2 separated working chambers, i.e., with multiple utilization of the working space of the housing, the same stroke provides a balanced force to the rotors and increases the power density of the engine.

Taking the spark ignition engine with six vane pistons per rotor for example, In Fig. 4, if the engine completes one cycle, which also means all components finish their tasks and back to the initial position, it requires one revolution of the output shaft and three power strokes for each of the work chambers, and completes 36 operative combustion processes. To sum up, this TRPE is equivalent to a 72-cylinder four-stroke conventional engine. Comparison of power density among different types of engines is given in Table 1.

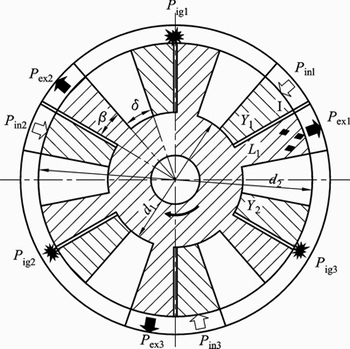
Fig. 4 An ECS with six vane pistons

Table 1 Comparison of power density among different types of engines

Additionally, with each stroke working in its respective zones of the ECS housing, the working chambers can be alternately utilized according to the power output requirements of the engine.

Three ignition devices (P_ig1, P_ig2, P_ig3), three intake ports (P_in1, P_in2, P_in3), and three exhaust ports (P_ex1, P_ex2, P_ex3) are radiately fixed at the circumference of the housing. Each stroke is commenced or completed while any working chamber travels close to the ports.

The compression ratio of the engine, e , can be expressed as

                                   (6)

where d_max and d_min are the maximum and minimum of d, which is the relative angle of the adjacent vane pistons. d is proportional to the volume of working chambers V, which is expressed as

                          (7)

where d₁ and d₂ are diameters of the inner and outer wall, of the working chamber, h is the depth of the working chamber in the axial direction.

The span angle of a vane piston is defined as b. A valid assumption can be that all the vane pistons have the same b. So,

                       (8)

Similar to the displacement definition of the conventional piston engine [5], the displacement of the TRPE engine, Q_ex, is defined as the gas volume exhausted from the 2N working chambers per revolution of the output shaft, which can be expressed as

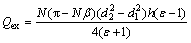           (9)

3.2 Kinematic model of two TRPE mechanisms

As rockers are fixed on their respective rotors, kinematic characteristics of the rotors can be obtained by analyzing the motion of the rockers. Taking DVDM-1 for example, as shown in Fig. 5, assuming OA, AB, OA', and A'B' are in coincidence with each other at the initial position. The positive direction of x-coordinate is defined from O to A. All angles are measured from the x-axis in the CCW direction. Thus, equations can be obtained from the loop closure method [29], which can be expressed as

    (10)

where 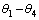are angles between components of the crank-rocker mechanism (OABC), 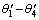are angles between components of the crank-rocker mechanism (OA′B′C′).

Both q₂ and q'₂ are equal to –iq₁. The angular velocity of all components can be obtained by differentiating Eq. (10) with respect to time (t), and the angular acceleration of all components by twice differentiating Eq. (10).

q_r is defined as the relative angle of the former rocker and the latter rocker, which can be expressed as

                                (11)

q_r is proportional to the angle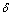, and their relation is

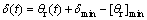                    (12)

where [q_r]_min is the minimum of the angle q_r. [q_r]_min is a constant with respect to time.

When some combustion chambers reach their maximum or minimum volumes, the angles d and q_r also simultaneously reach their maximum or minimum, and the following is obtained

                 (13)

The kinematic model of the DVDM-2 can also be established with the same method above.

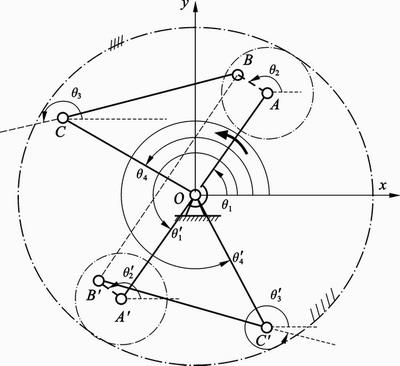
Fig. 5 Definitions of angles for kinematic analysis of DVDM-1

4 Comparison of two trPe mechanisms

The kinematic model developed in Section 3 is used to analyze characteristic of TRPE mechanisms. In this section, angular position, velocity, and acceleration of the two rockers are presented. The compression ratio and displacement of the two TRPE mechanisms are discussed.

The two TRPE mechanisms with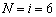, as shown in Fig. 2 and Fig. 3, are used as examples. Set l_AB =12 mm, l_BC=205 mm, l_OC=144 mm, r₁=125 mm, r₂=25 mm. A valid assumption can be that the planet gears of DVDM-1 and DVDM-2 are the same, and the stationary gears are also the same, i.e. r₃=r₁ and r₄=r₂. Substituting all above parameters into Eq. (10) with a numerical algorithm, the kinematic results of two TRPE mechanisms can be derived.

4.1 Position analysis

Figure 6 shows variations of angular positions of two rockers of DVDM-1 and DVDM-2 versus the output shaft angle. The motions of the two rockers have many similarities. On one hand, two rockers rotate with same pattern but at different paces, i.e., when one rocker accelerates, the other decelerates. On the other hand, the two continuously rotate in same direction, and one revolution of the rockers (taking DVDM-1 for example, one rotates from 94° to 454°, the other from 285° to 645°) is equivalent to one revolution of output crankshaft (from 0° to 360°).

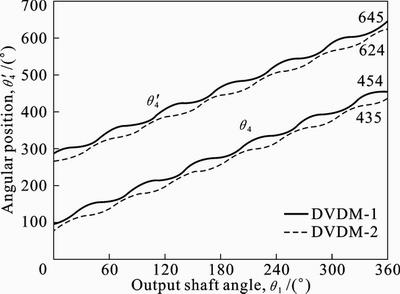
Fig. 6 Angular positions of two rockers of DVDM-1 and DVDM-2 versus output shaft angle

Table 2 gives the angular positions of the output shaft, the former rocker, and the latter rocker when V reaches its maximum/minimum For DVDM-1 and DVDM-2, when relative angle q_r reaches its maximum and the adjacent minimum, variation between two output shaft angles is p/N (here, as an example N=6, i.e, 30°, similar hereinafter), and the summation of two angles respectively covered by the two rockers is always equal to 2p/N. When V reaches its two adjacent maximums or minimums, variation between output shaft angles is equal to 2p/N.

Taking the two rockers in DVDM-1 for example, in the above process, the two rockers rotate 14.2° or 45.8° alternately. The summation is 60° and the difference is 31.6°. Thus, the variation amplitude of q_r in DVDM-1 is 31.6°, and it is larger than the variation amplitude of q_r in DVDM-2, which is 22.6°, i.e., the rockers of DVDM-1 are closer to (or farther from) each other than DVDM-2.

As shown in Fig. 7, q_r in DVDM-1 and DVDM-2 have same period which is equal to 2p/N, and q_r is proportional to 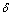. So, at the peak or valley of curves, working chambers reach their maximum volume. Also taking q_r in DVDM-1 for example, at the peak of continuous curve in Fig. 7 (q₁=7°+60°k, k is an arbitrary integer), working chambers denoted by odd number (I, III, V, VII, IX, XI) are at the start of exhaust or compression cycle while other working chambers are at the end of exhaust or compression cycle. At the valley of the curve (q₁=37°+60°k), working chambers with odd number are at the start of intake or power cycle while other working chambers are at the end of intake or power cycle.

4.2 Velocity analysis

The angular velocity of the rockers (or the respective rotors) can be obtained by assuming the angular velocity of the output shaft r/min. As shown in Fig. 8, the rotational speed of the rockers begins with a minimum angular velocity, then up to a maximum velocity, and again back to the minimum velocity. One rocker reaches its maximum angular velocity while the other rocker reaches its minimum angular velocity. The maximum/minimum volume of working chamber occurs when rockers’ speeds are momentarily identical. Taking working chambersⅠfor example, when q₁ is 7°, the volume of it reaches its maximum, and when q₁ is 37°, it reaches minimum.

As the output crankshaft rotates from a to b , shown in Fig. 9, working chambers I, V and IX, are performing the power stroke, II, VI and X are performing the compression stroke, III, VII and XI are performing the intake stroke, IV, VIII and XII are performing the exhaust stroke. Other phase of four-stroke cycle occurs in each working chamber in sequence.

Table 2 Angular positions of output shaft, former rocker, and latter rocker when V reaching its maximum/minimum

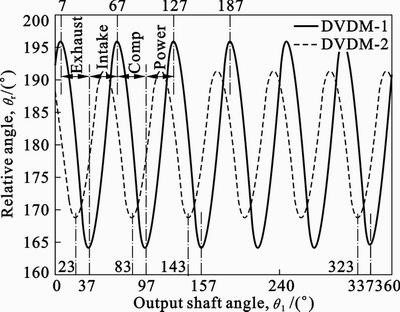
Fig. 7 Relative angle of two rockers versus output shaft angle

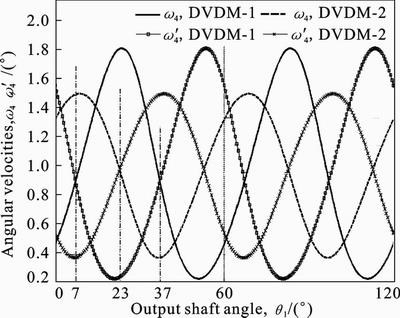
Fig. 8 Angular velocities of two rockers versus output shaft angle

The relative angular velocity (w₄–w'₄) in DVDM-1 and DVDM-2 has same near sinusoidal pattern. The average of both relative angular velocities is equal to zero and the period of both is equal to 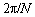. The minimum of (w₄–w'₄) in DVDM-1 is smaller than that in DVDM-2; the maximum of (w₄–w'₄) in DVDM-1 is bigger than that in DVDM-2. In addition, as the volumetric rate of change of the working chamber is proportional to the relative angular velocity, the volume of working chamber of DVDM-1 has sharper change than that of DVDM-2.

4.3 Acceleration analysis

Assuming w₁=1 rad/min and a₁=0, angular accelerations of the two rockers (or the two respective rotors) are illustrated in Fig. 10. Unlike angular velocity, which exhibits same patterns, angular acceleration of the former rocker and the latter rocker exhibits different patterns, i.e., angular acceleration functions of the former rocker and the latter rocker are totally different. The maximum angular acceleration of the former rocker and the minimum angular acceleration of the latter rocker occurs at different output shaft angles, and summation of the angular acceleration of the former rocker and the latter rocker is not equal to zero. As the value of the summation is proportional to inertia moment, which causes the knock tendency of the engine, some measures should be taken to eliminate the unbalance created by the inertia moment.

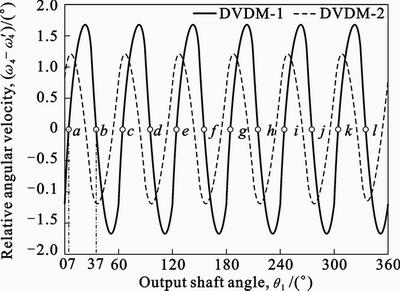
Fig. 9 Relative angular velocity of two rockers versus output shaft angle

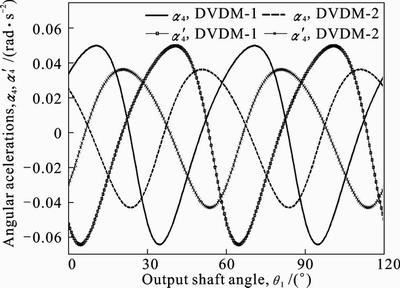
Fig. 10 Angular accelerations of two rockers versus output shaft angle

However, as shown in Fig. 11, the relative angular accelerations in DVDM-1 and DVDM-2 show the same sinusoidal-like pattern as the relative angular velocities, and both curves have the same 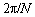period. Thus, the problem of above mentioned unbalance could be easily settled.

4.4 Compression ratio and displacement of engine

From the above analysis, the difference of the maximum and the minimum of q_r determined by the given parameters of DVDM. According to Eq. (13), the difference of the maximum and the minimum of 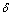can be derived, 31.6° in DVDM-1, and 22.6° in DVDM-2. If b is a known parameter, with Eqs. (6), (8) and (9), and Q_ex of the engine can also be derived. As shown in Fig. 12, as b increases, increases accordingly, while Q_ex decreases. In fact, on one hand, the higher value of, the higher the efficiency of the engine; On the other hand, the higher the value of Q_ex, the more the output power of the engine.

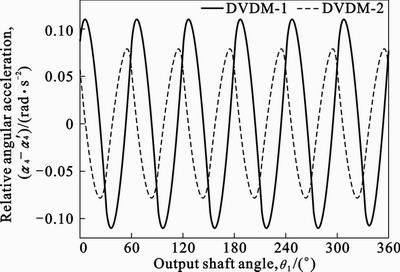
Fig. 11 Relative angular acceleration of two rockers versus output shaft angle

Set d₁=150 mm, d₂=300 mm, h=80 mm. In order to assure high efficiency and high output power of the engine simultaneously, with above parameters, in DVDM-1, b should be 10.2°, and the value of e is 10°; in DVDM-2,should be 10.6°, and the value of is 4.3.

Fig. 12 Compression ratio and displacement of engine versus span angle of vane piston:

4.5 Simulation

In order to validate above kinematic results, a 3D model of DVDM-1 built in software ADAMS is presented. In Fig. 13, as the output shaft (or the planet carrier) rotates from 7° to 37°, the vane piston Y₁ will gradually occupy the position of the vane piston L₁, and the vane piston L₁ will gradually occupy the position of the vane piston Y₂, and the vane piston Y₂ will gradually occupy the position of the vane piston L₂. The simulation results also show that vane pistons Y₁–Y₆ cover 45.8° and vane pistons L₁– L₆ cover 14.2° in above period.

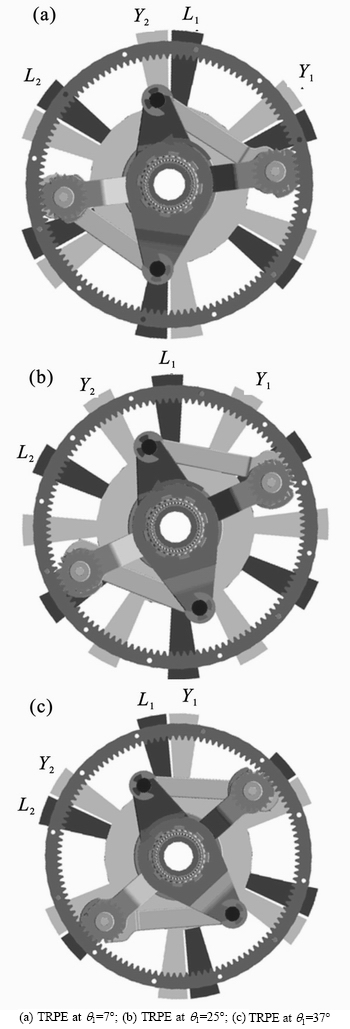
Fig. 13 Simulation results of TRPE with DVDM-1 with housing removed:

5 Conclusions

1) Both DVDM-1 and DVDM-2 create N² power strokes per revolution of the output shaft.

2) Relative angular velocities of the two rotors in DVDM-1 and DVDM-2 have same near sinusoidal relative motion with an average relative speed of zero and a period of 2p/N, which could maintain steady engine operation.

3) As the output shaft rotates an angle of p/N, the summation of two angles covered by each rocker is always 2p/N.

4) The variation amplitude of relative angle of two rockers in DVDM-1 is larger than that of DVDM-2, so positions of intake ports and exhaust ports are different.

References

[1] KORAKIANITIS T, BORUTA M, JEROVSEK J, MEITNER P L. Performance of a single nutating disk engine in the 2 to 500 kW power range [J]. Applied Energy, 2009(86): 2213–2221.

[2] NITULESCU O. Numerical simulation of the thermodynamics of a nutating engine [D]. Toledo: The University of Toledo, 2006.

[3] MIKALSEN R, ROSKILLY A P. A review of free-piston engine history and applications [J]. Applied Thermal Engineering, 2007, 27(14/15): 2339-2352.

[4] HE Wei, WU Yu-ting, MA Chong-fang, MA Guo-yuan. Research of air powered engine system using two-stage single screw expander [J]. Chinese Journal of Mechanical Engineering, 2010, 46(10): 139–143. (in Chinese)

[5] STONE R. Introduction to Internal Combustion Engines [M]. New York: MacMillian, 1999: 2–8.

[6] LING Da-yuan, LIANG Zhao-ji, WANG Jing-hu, ZHU xian-ding. A preliminary inquiry into the problems of the power transmission mechanism for internal combustion engine [J]. Transactions of CSICE, 1985, 8(4): 301–313. (in Chinese)

[7] ROSENKRANZ H G. CMC scotch Yoke engine technology [D]. Victoria: Melbourne University, 1998.

[8] KARHULA J. Cardan gear mechanism versus slider-crank mechanism in pumps and engines [D]. Finland: Lappeenranta University of Technology, 2008.

[9] ZHOU Nai-ju, PEI Hai-ling, ZHANG Jia-qi, CHEN Hong-de. Mathematic models for thermodynamic process of rotary combustion engine [J]. Journal of Central South University: Science and Technology, 2008, 39(3): 284-288. (in Chinese)

[10] YAMAMOTO K. Rotary engine [M]. Sankaido Co., Ltd, Tokyo, Japan, 1981: 4–10.

[11] ASHLEY, S. A new spin on the rotary engine [J]. Mechanical Engineering, 1995, 117(4): 80–82.

[12] HUDSON B. The production of power by pure rotary means [D]. Melbourne: RMIT University, Australia, 2008: 1–10.

[13] ERTESVAG I S. Analysis of the vading concept-a new rotary-piston compressor, expander and engine principle [C] // Proc of Institution of Mechanical Engineers, Part A: J. of Power and Energy, 2002(216): 283–289.

[14] ROY J. Development of a rotary vane gas cycle heat engine [C] // 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, 2008: AIAA 2008–4703.

[15] KAUERTZ E. Rotary radial-piston machine: United States Patent, US 3, 44, 07 [P]. 1967.

[16] SAKITA M. Rotary pison engine: United States Patent, US 6,446,595 B1 [P]. 2002.

[17] SAKITA M. A cat-and-mouse type rotary engine: engine design and performance evaluation [J]. Proc of the Institution of Mechanical Engineering, Part D: Journal of Automobile Engineering, 2006, 220: 1139–1151.

[18] LIBROVICH B, TUCKER R W, WANG C. On gear modeling in multistage rotary vane engines [J]. Meccanica, 2004, 39, 47–61.

[19] LIBROVICH B. Analysis, design, and modeling of a rotary vane engines [J]. Journal of Mechanical Engineering, 2004, 126(4), 711–718.

[20] CHENG Ming, Zi Jin-feng, Zhang Yong, Li Gui-xian. Study of a differential velocity vane pump driven by Hooke’s joints [J]. Chinese Mechanical Science and technology, 2006, 25(11): 1298–1302. (in Chinese)

[21] CHENG Ming, WANG Guang-lin, LIU Fu-li, LI Xiao, LI Gui-xian. study of eccentric circular-noncircular gears driving system of differential velocity vanes pump [J]. Chinese Journal of Mechanical Engineering, 2005, 41(3): 98–101. (in Chinese)

[22] LIANG L. A rotary engine with two rotors and its design method: World Patent, WO 2005/124122 A1 [P]. 2005.

[23] CHUN H F. Alternative-step appliance rotary piston engine: United States Patent, US 2004/0261758 A1 [P]. 2004.

[24] Morgado R G. Internal combustion engine and method. United States Patent, US 20070199537A1 [P]. 2007.

[25] OMORI T. Cat and mouse type internal combustion engine, and its correlation type crank: United States Patent, US 2010/0180858A1 [P]. 2010.

[26] WIESLAW J O. About a new concept of internal combustion engine construction I. rotary engines [C] // Proc of IMECE, ASME, Boston, Massachusetts, USA, 2008–66297.

[27] PAN Cun-yun, ZHAO Yun-wen, DENG Hao. A four-rotors piston engine: China, 201110071263.8 [P]. 2011–03–24. (in Chinese)

[28] PAN Cun-yun, ZHAO Yun-wen, DENG Hao. power transmission equipment in positive displacement machine: china, 201110071446. X [P]. 2011-03-24. (in Chinese)

[29] LI T, CAO W. Kinematic analysis of geared linkage mechanisms [J]. Mechanism and Machine Theory, 2005 (40): 1394–1413.

(Edited by HE Yun-bin)

Foundation item: Project(7131109) supported the by National Defense Pre-research Foundation of China; Project(50975278) supported by National the Natural Science Foundation of China

Received date: 2011–12–05; Accepted date: 2012–03–22

Corresponding author: DENG Hao, PhD;Tel: +86-731-84574932;E-mail: aaron_dh@163.com

Abstract: A novel twin-rotor piston engine (TRPE) mechanism with high volumetric output and power density was introduced. This new engine comprises an energy conversion system and a differential velocity drive mechanism (DVDM). Two special geared four-bar mechanisms, DVDM-1 and DVDM-2, were utilized and compared. Based on the closed loop vector method, a mathematical model for position, velocity, and acceleration of the two mechanisms was established. Numerical examples illustrate that the kinematic characteristics were presented. Expression of the displacement and compression ratio of the two engine mechanisms were derived and compared. It is concluded that both DVDM-1 and DVDM-2 adopted in the proposed TRPE with six vane pistons create thirty-six power strokes per revolution of the output shaft, and the summation of two angles covered by each rocker is always 2p/N as the output shaft rotates an angle of p/N. In DVDM-1, the span angle of a vane piston should be designed to be 10.2°, and the compression ratio should be equal to 10; in DVDM-2, the span angle of a vane piston should be designed to be 10.6°, and the compression ratio should be equal to 4.3.