利用剪切效应原理计算双模量材料的性能参数解
吴晓,杨立军,黄志刚
(湖南文理学院 土木建筑工程学院,湖南 常德,415000)
摘 要:
理证明作用在双模量梁上的横向载荷对中性轴位置没有影响。在考虑剪切效应的基础上,建立双模量梁弯曲的微分方程,推导出双模量梁的挠曲线表达式。研究结果表明:利用三点弯曲法及四点弯曲法可方便地求出双模量材料的性能参数;该测定双模量材料的性能参数的试验方法简便可行而且精度较高,可同时测出双模量梁的弯曲刚度及剪切刚度,且能够保证弯曲刚度与剪切刚度具有相同的实验精度;该试验方法不但可以测定双模量材料的性能参数,而且可以测定复合材料的性能参数和各向同性材料的性能参数,具有较强的通用性。
关键词:
中图分类号:O341 文献标志码:A 文章编号:1672-7207(2014)02-0609-06
Calculating performance parameters of bimodulous material with shear effect principle
WU Xiao, YANG Lijun, HUANG Zhigang
(College of Architecture & Civil Engineering, Hunan University of Arts and Science, Changde 415000, China)
Abstract: It was proved that lateral loads acting on bimodulous beam have no effect on the position of the neutral axis. Considering the shear effect, the differential equation of bimodulous beam bending was established, and the deflection expression of bimodulous beam was deduced. The results show that performance parameters of bimodulous material can be easily obtained with three-point bending method and four-point bending method. The experimental method for the determination of bimodular materials performance parameters is simple and feasible and has high precision, which can simultaneously measure the bending mode of the beam stiffness and shear stiffness, and can ensure the bending stiffness and shear stiffness of the same precision. The performance parameters of the experimental method can not only determine bimodular materials performance parameters, but also measure composite material performance parameters and isotropic material, which shows this method has strong universality.
Key words: shear effect; bimodulous; material; bending
在工程实际中,许多材料都具有拉压弹性模量不同的双模量特性。文献[1-4]分析了双模量材料板的变形;文献[5-7]分析了双模量材料板、圆柱壳的动力特性;文献[8]对一种在多工况载荷下的双模材料进行了优化设计;文献[9]采用细观力学研究了双模量泡沫材料等效弹性模量;文献[10-11]研究了双模量材料的本构关系;文献[12-15]对双模量材料结构弯曲及扭转变形进行了计算分析,而对双模量材料进行计算分析的前提条件是要先确定双模量材料的弹性模量等性能参数。可见,对双模量材料结构进行计算设计,测定双模量材料的弹性模量等性能参数是非常必要的。文献[16]采用单轴拉伸及压缩试验测定了有机玻璃的拉伸及压缩弹性模量,然后,利用应变公式推算出了有机玻璃的剪切弹性模量。文献[17]利用三点弯曲法、四点弯曲法测定了复合材料的弯曲模量,利用平面剪切试验测定了剪切弹性模量。GB/T 5166—1998(《烧结金属材料和硬质合金弹性模量测定》)[18]规定对试样超声波纵向振动进行激发,然后测定其固有的共振频率,以此来推算试样的弹性模量。文献[19]研究了WC-Co 超细硬质合金的超声波无损检测;文献[20]综述了WC-Co 硬质合金的弹性性能。超声波纵向振动法虽然是无损测试,但成本比较高,在生产实际中不便于推广使用。为此,本文作者在考虑剪切效应的基础上,利用三点弯曲法及四点弯曲法测定有机玻璃外伸简支梁的中点及端点的挠度,并根据测定的中点及端点的挠度计算剪切刚度。同时,为了说明本文方法在测定各向同性材料中性能参数的应用,还测定了硬质合金弹性模量和剪切弹性模量。
1 中性轴位置的确定
双模量梁在横向载荷作用下弯曲时,会形成弹性模量不同的拉伸区和压缩区,由弹性理论可知双模量梁弯曲时的应力和应变关系为
 ,
, (1)
(1)
式中:E1和E2分别为双模量梁受拉、受压弹性模量;ρ为双模量梁弯曲曲率;σ1和σ2分别为双模量梁拉应力和压应力;y为双模量梁横截面内与中性轴垂直的轴的坐标。
假设图1所示双模量简支梁在任意载荷作用下发生弯曲变形,以A点为力矩支点可知:
 (2)
(2)
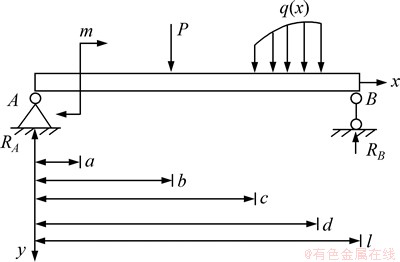
图1 载荷作用下双模量梁
Fig. 1 Bimodulous beam under loads
式中:RB为简支梁在支座B的支反力;P,m和q(x)分别为作用在简支梁上的任意集中荷载、力矩和分布荷载;l为简支梁跨度;b为集中荷载作用点的坐标;c和d分别分布荷载始、末点坐标。
由式(2)可以求得简支梁的支反力RA和RB为
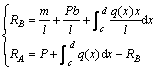 (3)
(3)
简支梁的支座约束反力确定后,即可方便写出简支梁任意截面的弯矩表达式M(x)。
由弹性理论可知双模量梁弯曲时横截面内力应满足以下关系:
 (4)
(4)
虽然双模量梁在任意载荷作用下其横截面弯矩在不同梁段是不相同的,但其曲率是轴向坐标的函数且与梁高无关,将式(1)代入式(4)得:
 ,
, (5)
(5)
式中:h1为拉伸区高度;h2为压缩区高度;h=h1+h2; 。
。
由以上推导可知:双模量梁中性轴的位置与作用在其梁上的横向载荷无关。
2 双模量梁挠曲线表达式
考虑剪切效应的影响时,可知双模量梁的挠度为弯曲挠度wb与剪切挠度wc之和,即
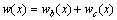 (6)
(6)
由于剪应变用剪切挠度可表示为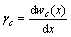 ,考虑剪切虎克定律时,
,考虑剪切虎克定律时,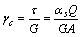 ,所以,
,所以,
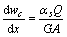 (7)
(7)
式中:αs为剪切系数;G为剪切弹性模量;A为横截面积;Q为剪力。
由式(7)可知剪切效应产生的曲率为
 (8)
(8)
式中: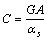 。所以,双模量梁总挠度曲线的曲率微分方程为
。所以,双模量梁总挠度曲线的曲率微分方程为
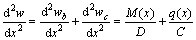 (9)
(9)
对式(9)连续进行积分可得:
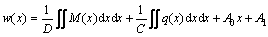 (10)
(10)
式中:A0和A1为积分常数,可利用梁边界条件确定。以三点弯曲法、四点弯曲法为例,可知双模量简支梁的边界条件为
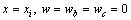 (11)
(11)
以图1所示的双模量简支梁为例,当梁中点仅有集中载荷P作用时,由式(10)和(11)可求得梁中点挠度为
 (12)
(12)
3 双模量性能参数的计算原理
对于图2所示双模量外伸简支梁,由Betti-Rayleigh互等定理可知有下式成立:
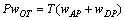 (13)
(13)
式中:wOT为T力分别作用在梁端A和D点时梁中点的挠度;wAP和wDP分别为P力作用在梁中点时A和D点的挠度。

图2 双模量外伸简支梁
Fig. 2 Bimodulous overhang
从图2(a)可知:wAP=wDP=H。 所以,当 时,式(13)可化为
时,式(13)可化为
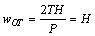 (14)
(14)
当T力作用在图2(b)所示的A和D点时,梁BC段为纯弯曲,因此,梁BC段内弯曲曲率处处相等,由材料力学理论可求得:
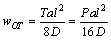 (15)
(15)
由式(14)和(15)可知双模量外伸简支梁的弯曲刚度为
 (16)
(16)
将式(16)代入式(12)可得:
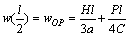 (17)
(17)
当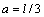 时,式(17)可化为
时,式(17)可化为
 (18)
(18)
式(18)表明:当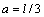 ,即图2(b)所示双模量外伸简支梁四点弯曲时,其中点挠度恰好与图2(a)所示的双模量外伸简支梁三点弯曲时的中点挠度的弯曲挠度相等,所以,当wOP经试验确定为已知时,即可确定双模量梁的剪切刚度为
,即图2(b)所示双模量外伸简支梁四点弯曲时,其中点挠度恰好与图2(a)所示的双模量外伸简支梁三点弯曲时的中点挠度的弯曲挠度相等,所以,当wOP经试验确定为已知时,即可确定双模量梁的剪切刚度为
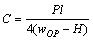 (19)
(19)
4 双模量性能参数的实验结果
由于有机玻璃是典型的双模量材料,因此,以有机玻璃为例作为本文实验方法的应用示例。文献[16]测定出的有机玻璃弹性模量E1=1.72×105 MPa,E2=2.95×105 MPa,然后,根据实验测定出的弹性模量计算出的剪切弹性模量G=0.798 8×105 MPa。本文实验有机玻璃试件的宽度b=10 mm,加载载荷P=2 kN。根据以上计算原理,设计本文实验方案见图3,实验测定出的有机玻璃梁A和D点的挠度H及中点挠度wOP的实验结果见表1和表2。
将表1有机玻璃梁A和D点的挠度H的实验结果及表2中有机玻璃梁的中点挠度wOP代入式(16)和(19),可计算出有机玻璃梁的弯曲刚度D及剪切刚度C,具体结果可表3和表4。
将文献[16]中测定出的有机玻璃弹性模量代入式

图3 实验方案
Fig. 3 Experimental program
表1 h=5 mm时有机玻璃梁A和D点的挠度H实验结果
Table 1 Experimental results of point A and D deflection H of perspex beam mm

表2 h=5 mm时有机玻璃梁的中点挠度wOP的实验结果
Table 2 Experimental results of midpoint deflection wOP of perspex beam when h is 5 mm mm

(5)可知D=23.042 4 N·m2,而表3所示有机玻璃的弯曲刚度实验结果平均值D=23.024 0 N·m2,两者相对误差为0.08%。将表4中的有机玻璃梁的剪切刚度实验结果代入式(19),可知有机玻璃剪切弹性模量平均值G=0.812 5×105 MPa,文献[16]根据实验测定出的弹性模量计算出的剪切弹性模量G=0.798 8×105 MPa,两者相对误差为1.72%。由以上实验结果及计算结果可以看出:本文实验结果与文献[16]中的实验结果较吻合,这说明本文测定双模量材料性能参数的实验方法简便可行,精度较高,而且可以同时测出有机玻璃梁的弯曲刚度及剪切刚度,能够保证弯曲刚度与剪切刚度具有相同的实验精度。
为了进一步证明本文方法的可靠性且在测定各向同性材料中性能参数的应用效果,下面以厦门金鹭特种合金股份有限公司生产的硬质合金精磨圆棒作为试样,硬质合金试样直径d=3 mm。图3所示的外伸简支梁跨距l=30 mm,外伸长a=10 mm。本试验在CMT5305电子万能试验机上进行,试验压力示值误差在±0.5%以内,挠度分辨率为0.015 μm,仪器精密度等级为0.5级。对试样与支承之间进行润滑,在梁中点用压头施加压力使梁发生弯曲产生挠度。当压力为0~100 N时,压头加载速度为0.5 mm/min;当压力大于100 N时,加载速度为0.25 mm/min,加载载荷P=500 N。硬质合金试样的具体牌号见表5,合金中Co质量分数以RTP配料中Co质量分数代替。由于第1次测试的挠度结果通常误差较大,所以,试验只采用第2~5 次测试的挠度试验结果,并计算测试的挠度平均值。试验测试的挠度平均值见表6和表7。将表6中测试梁上A和D点挠度wAP和wDP平均值代入式(16)即可算得硬质合金的弹性模量E,见表8。同理,将表7中测试梁上O点挠度wOP平均值代入式(19)即可算得硬质合金的剪切弹性模量G,见表9。
分析表5~9可以看出:随着硬质合金中Co质量分数的增大,硬质合金外伸简支梁的中点挠度逐渐增大,而硬质合金弹性模量和剪切弹性模量逐渐减小,即硬质合金弹性模量剪切弹性模量随着Co质量分数的增大而减小。表9中的试验结果与文献[21]中硬质合金等效弹性性能预测方法计算结果变化趋势基本一致,但文献[22]中的预测方法是利用数学模型进行理论计算得出,显然其得到的结果是近似的。表9中的试验结果与文献[22]中的结果较吻合,这说明本文利用三点弯曲法测定硬质合金材料性能参数得到的试验结果是可靠的。
表3 h=5 mm时有机玻璃梁的弯曲刚度D实验结果
Table 3 Experimental results of shear stiffness D of perspex beam when h is 5 mm N·m2

表4 h=5 mm时有机玻璃梁的剪切弹性模量实验结果
Table 4 Experimental results of shear modulus of perspex beam when h is 5 mm

表5 试样的硬质合金牌号、WC 平均晶粒度和硬质合金中Co的名义质量分数
Table 5 Trade-name, average WC granularity and nominal cobalt mass fraction of cemented carbides
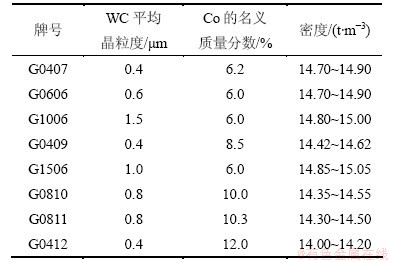
表6 试样的硬质合金的A和D点挠度H的测量结果
Table 6 Experimental results of point A and D deflection H of cemented carbides mm

表7 试样的硬质合金的中点挠度wOP的测量结果
Table 7 Experimental results of midpoint deflection wOP of cemented carbides mm

表8 试样的硬质合金弹性模量E 计算结果
Table 8 Calculation results of elastic modulus E of cemented carbides GPa

表9 试样的硬质合金的剪切弹性模量G的计算结果
Table 9 Calculation results of shear modulus G of cemented carbides GPa

以上试验结果表明:本文测定双模量、各向同性材料的性能参数的实验方法简便可行而且精度较高,可同时测出双模量、各向同性材料梁的弯曲刚度及剪切刚度,且能够保证弯曲刚度与剪切刚度具有相同的实验精度。该实验方法不但可以测定双模量、各向同性材料的性能参数,而且可以测定复合材料的性能参数,所以,该实验方法具有较强的通用性,完全可以在实际工程中推广使用。
5 结论
(1) 采用材料力学原理证明了作用在双模量梁上的横向载荷对中性轴位置无影响。
(2) 在考虑剪切效应的基础上,建立了双模量梁弯曲的微分方程,推导出双模量梁的挠曲线表达式。利用三点弯曲法及四点弯曲法,即可方便地求出双模量材料、各向同性材料的性能参数。
(3) 本文测定双模量、各向同性材料的性能参数试验方法不但简便可行,精度较高,而且可以同时测出双模量、各向同性材料弹性模量、剪切弹性模量,能够保证双模量、各向同性材料弹性模量、剪切弹性模量具有相同试验精度。本文的试验方法具有较强的通用性,可以在实际工程中推广使用。
(4) 本文利用三点弯曲法及四点弯曲法的实验方法不但可以测定双模量材料、各向同性材料的性能参数,而且可以测定复合材料的性能参数。
参考文献:
[1] Medri G. A nonlinear elastic model for isotropic materials with different behaviors in tension and compression [J]. Transactions of the ASME, 1982, 26: 26-28.
[2] Srinivasan R S, Ramachandra L S. Axisymmetric nonlinear dynamic response of bimodulous annular plates[J]. Journal of Vibration and Acoustics, 1990, 112(2): 202-205.
[3] He X T, Sun J Y, Wang Z X, et al. General perturbation solution of large-deflection circular plate with different moduli in tension and compression under various edge conditions[J]. International Journal of Nonlinear Mechanics, 2013, 55(10): 110-119.
[4] He X T, Chen Q, Sun J Y, et al. Large-deflection axisymmetric deformation of circular clamped plates with different moduli in tension and compression[J]. International Journal of Mechanical Sciences, 2012, 62(1): 103-110.
[5] Patel B P, Gupta S S, Joshi M, et al. Transient response analysis of bimodulus anisotropic laminated composite plates[J]. Journal of Reinforced Plastics and Composites, 2005, 24(8): 795-821.
[6] Patel B P, Gupta S S, Sarda R. Free flexural vibration behavior of bimodular material angle-ply laminated composite plates[J]. Journal of Sound and Vibration, 2005, 286(1): 167-186.
[7] Khan K, Patel B P, Nath Y. Vibration analysis of bimodulus laminated cylindrical panels[J]. Journal of Sound and Vibration, 2009, 321(2): 166-183.
[8] Cai K, Gao Z L, Shi J. Compliance optimization of a continuum with bimodulus material under multiple load cases[J]. Computer-Aided Design, 2013, 45(2): 195-203.
[9] 李战莉, 黄再兴. 双模量泡沫材料等效弹性模量的细观力学估算方法[J]. 南京航空航天大学学报, 2006, 38(4): 464-468.
Li Zhanli, Huang Zaixing. Meso-mechanical method for estimating equivalent elastic modulus of foam-solid with double-modulus[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2006, 38(4): 464-468.
[10] 蔡来生, 俞焕然. 拉压模量不同弹性物质的本构[J]. 西安科技大学学报, 2009, 29(1): 17-21.
Cai Laisheng, Yu Huanran. Constitutive relation of elastic materials with different elastic moduli in tension and compression[J]. Journal of Xi’an University of Science and Technology, 2009, 29(1): 17-21.
[11] Patel B P, Khan K, Nath Y. A new constitutive model for bimodular laminated structures: Application to free vibrations of conical/cylindrical panels[J]. Composite Structures, 2014, 110(1): 183-191.
[12] 吴晓, 杨立军, 孙晋. 双模量圆板弯曲变形的计算分析[J]. 西安建筑科技大学学报(自然科学版), 2009, 41(1): 88-92.
WU Xiao, Yang Lijun, SUN Jin. Bending deformation calculation of bimodulous circular plate[J]. Journal of Xi’an University of Architecture & Technology (Natural Science Edition), 2009, 41(1): 88-92.
[13] 吴晓, 黄翀, 孙晋. 双模量悬臂梁在分布载荷作用下的Kantorovich解[J]. 湖南科技大学学报(自然科学版), 2012, 27(2): 55-59.
WU Xiao, HUANG Chong, SUN Jin. The Kantorovich solution for bimodulous cantilever under distributed loads[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2012, 27(2): 55-59.
[14] 吴晓, 杨立军, 孙晋. 用双模量理论分析灰铸铁拉伸与扭转的破坏试验[J]. 湖南科技大学学报(自然科学版), 2011, 26(3): 51-54.
WU Xiao, Yang Lijun, SUN Jin. Bimodulous theory analysis for gray cast iron failure experiment in tension and torsion[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2011, 26(3): 51-54.
[15] 吴晓. 用Kantorovich及Galerkin联合法研究双模量板的弯曲[J]. 西安建筑科技大学学报(自然科学版), 2012, 44(4): 457-461.
WU Xiao. Kantorovich and Galerkin solution to the bending of bimodulous plate[J]. Journal of Xi’an University of Architecture & Technology (Natural Science Edition), 2012, 44(4): 457-461.
[16] 施明泽, 卢锡如. 有机玻璃受拉与受压弹性常数的测定及其与剪切弹性模量的关系[J]. 理化检验: 物理分册, 1991, 27(3): 42-43.
SHI Mingzhe, LU Xiru. Determination of elastic constants in tension and compression of perspex and the relationship between them and shear elasticity modulus[J]. Physical Testing and Chemical Analysis Part A: Physical Testing, 1991, 27(3): 42-43.
[17] 张双寅, 刘济庆, 于晓霞, 等. 复合材料结构的力学性能[M]. 北京: 北京理工大学出版社, 1990: 120-126.
Zhang Shuangyin, Liu Jiqing, YU Xiaoxia, et al. Mechanical properties of structure of composite material[M]. Beijing: Beijing Institute of Technology Press, 1990: 120-126.
[18] GB/T 5166—1998, 烧结金属材料和硬质合金弹性模量测定[S].
GB/T 5166—1998, Sinteredmetal materials and hard metals determination of Young modulus[S].
[19] 闫丽, 邵刚勤, 熊震, 等. WC-Co 超细硬质合金的超声波无损检测[J]. 武汉理工大学学报, 2007, 29(10): 153-157.
YAN Li, SHAO Gangqin, XIONG Zhen, et al. Ultrasonicevaluation of WC-Co hard metals[J]. Journal of Wuhan University of Technology, 2007, 29(10): 153-157.
[20] 李安海, 赵军, 王泽明, 等. WC-Co 硬质合金的弹性性能[J]. 硬质合金, 2011, 28(3): 194-198.
LI Anhai, ZHAO Jun, WANG Zeming, et al. Elastic properties of WC-Co cemented carbideds[J]. Cemented Carbide, 2011, 28(3): 194-198.
[21] 王泽民. WC-Co硬质合金微观结构建模及性能预测[D]. 济南: 山东大学机械工程学院, 2012: 30-38.
Wang Zemin. Microstructure modelling and properties prediction of WC-Co cemented carbides[D]. Jinan: Shandong University. College of Mechanical Engineering, 2012: 30-38.
[22] Upadhyaya G S. Materials science of cemented carbides: An overview[J]. Materials & Design, 2001, 22(6): 483-489.
(编辑 陈灿华)
收稿日期:2013-04-10;修回日期:2013-06-27
基金项目:湖南省科技计划项目(湘财企指[2011]65号);湖南省“十二五”重点建设学科资助项目(湘教发2011[76])
通信作者:杨立军(1976-),男,湖南邵阳人,副教授,从事结构振动理论研究;电话:15873665127;E-mail:yanglj9601@163.com
摘要:采用材料力学原理证明作用在双模量梁上的横向载荷对中性轴位置没有影响。在考虑剪切效应的基础上,建立双模量梁弯曲的微分方程,推导出双模量梁的挠曲线表达式。研究结果表明:利用三点弯曲法及四点弯曲法可方便地求出双模量材料的性能参数;该测定双模量材料的性能参数的试验方法简便可行而且精度较高,可同时测出双模量梁的弯曲刚度及剪切刚度,且能够保证弯曲刚度与剪切刚度具有相同的实验精度;该试验方法不但可以测定双模量材料的性能参数,而且可以测定复合材料的性能参数和各向同性材料的性能参数,具有较强的通用性。
[9] 李战莉, 黄再兴. 双模量泡沫材料等效弹性模量的细观力学估算方法[J]. 南京航空航天大学学报, 2006, 38(4): 464-468.
[10] 蔡来生, 俞焕然. 拉压模量不同弹性物质的本构[J]. 西安科技大学学报, 2009, 29(1): 17-21.
[12] 吴晓, 杨立军, 孙晋. 双模量圆板弯曲变形的计算分析[J]. 西安建筑科技大学学报(自然科学版), 2009, 41(1): 88-92.
[13] 吴晓, 黄翀, 孙晋. 双模量悬臂梁在分布载荷作用下的Kantorovich解[J]. 湖南科技大学学报(自然科学版), 2012, 27(2): 55-59.
[14] 吴晓, 杨立军, 孙晋. 用双模量理论分析灰铸铁拉伸与扭转的破坏试验[J]. 湖南科技大学学报(自然科学版), 2011, 26(3): 51-54.
[15] 吴晓. 用Kantorovich及Galerkin联合法研究双模量板的弯曲[J]. 西安建筑科技大学学报(自然科学版), 2012, 44(4): 457-461.
[16] 施明泽, 卢锡如. 有机玻璃受拉与受压弹性常数的测定及其与剪切弹性模量的关系[J]. 理化检验: 物理分册, 1991, 27(3): 42-43.
[17] 张双寅, 刘济庆, 于晓霞, 等. 复合材料结构的力学性能[M]. 北京: 北京理工大学出版社, 1990: 120-126.
[18] GB/T 5166—1998, 烧结金属材料和硬质合金弹性模量测定[S].
[19] 闫丽, 邵刚勤, 熊震, 等. WC-Co 超细硬质合金的超声波无损检测[J]. 武汉理工大学学报, 2007, 29(10): 153-157.
[20] 李安海, 赵军, 王泽明, 等. WC-Co 硬质合金的弹性性能[J]. 硬质合金, 2011, 28(3): 194-198.
[21] 王泽民. WC-Co硬质合金微观结构建模及性能预测[D]. 济南: 山东大学机械工程学院, 2012: 30-38.


