
J. Cent. South Univ. (2020) 27: 356-371
DOI: https://doi.org/10.1007/s11771-020-4301-6

Influence of abrasive hardness on erosion wear of abrasive air jets
LIU Yong(刘勇)1, 2, CHEN Chang-jiang(陈长江)1, 2, WEI Jian-ping(魏建平)1, 2,LIU Xiao-tian(刘笑天)3, WANG Xiang-dong(王向东)4
1. State Key Laboratory Cultivation Base for Gas Geology and Gas Control, Henan Polytechnic University, Jiaozuo 454000, China;
2. State Collaborative Innovation Center of Coal Work Safety and Clean-efficiency Utilization,Jiaozuo 454000, China;
3. Safety Technology Training Institute, Henan Polytechnic University, Jiaozuo 454000, China;
4. Huajin Coking Coal Co., Ltd., Lüliang 033000, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract:
To make clear the influence of abrasive hardness on the erosion effect, the erosion experiments of abrasive air jet with the same impact energy were carried out. The influence of abrasive hardness on the erosion effect is clarified by comparing the different erosion depths. The main conclusions are as follows. Under the same mass flow rate and mesh number, the abrasive with a higher density needs greater pressure irrespective of hardness. After erosion damage, the abrasive size exhibits a Weibull distribution. The shape parameter β and Weibull distribution function of four types of abrasives are derived by the least squares method; moreover, β is found to have a quadratic relation with abrasive hardness. The results of the erosion experiments show that abrasive hardness and erosion depth are quadratically related. By calculating the increase in surface energy after abrasive erosion crushing, it is found that abrasive hardness has a quadratic relation with surface energy and that the increases in erosion depth and surface energy consumption are basically identical. In conclusion, the effect is a soft abrasive impact when the ratio of abrasive hardness (Ha) to the material hardness (Hm) is <2.6, and it is a hard abrasive impact when Ha/Hm >3.
Key words:
abrasive air jet; abrasive hardness; rock erosion; abrasive size distribution; coal bed methane;
Cite this article as:
LIU Yong, CHEN Chang-jiang, WEI Jian-ping, LIU Xiao-tian, WANG Xiang-dong. Influence of abrasive hardness on erosion wear of abrasive air jets [J]. Journal of Central South University, 2020, 27(2): 356-371.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-020-4301-61 Introduction
During the extraction processes of coal bed methane (CBM), the infiltrating and softening effect of water in coal is significant during water jet-assisted drilling and completion. This is due to the well-developed natural fractures and stratifications of coal reservoirs, which result in the frequent collapse of borehole walls during drilling and completion [1-5]. The use of auxiliary drilling using waterless technology, such as high-pressure abrasive gas jet-assisted drilling, prevents these problems. Abrasive gas jets are broadly used in applications such as surface finishing, surface treatment, drilling, and grooving [6-9]. Owing to their high impact performance, abrasive gas jets are widely used for coal breaking, pressure relieving, and permeability enhancement to improve the extraction efficiency of CBM reservoirs [10-12]. In soft coal seams, in particular, these jets can prevent the negative effects of hydraulic measures on gas desorption and transport [13] [Chen, 2017, Mechanism of the Two-Phase Flow Model for Water and Gas Based on Adsorption and Desorption in Fractured Coal and Rock]. The key determinant of auxiliary drilling efficiency is the erosion performance of the abrasive jet, which depends on the jet’s pressure and abrasive parameters [9, 14-16]. Jet pressure is limited by the high-pressure gas-compression pump used and the engineering application being considered. Assuming a limited jet pressure, it thus seems particularly important to analyze the influence of the abrasive parameters on coal breaking when using high-pressure abrasive gas jets. The main parameters affecting the erosion performance of abrasives include particle size, density, and hardness [17-20]. Among them, particle size and density are the mass-related terms in the impact kinetic energy calculations of abrasives. Under fixed gas jet parameters, the inertia of the particles affects their acceleration. Within a certain range of particle sizes, erosion rate increases with particle size; however, this rate remains almost unchanged after the particle size reaches a certain threshold [21, 22]. For example, the erosion rate reaches the peak for an equivalent circular area diameter of approximately 50 μm for SiC particles. Similar erosion-leveling trends have also been observed for Al2O3 particles of more than 35 μm in area diameter [23]. The main reason for this is that an increase in particle size leads to a decreased impact velocity of the abrasive, and thus, there is no increase in the impact kinetic energy. At present, the commonly used erosion-rate models properly integrate the target erosion effects of abrasive mass and velocity [9, 24]. Nonetheless, all these models ignore the effects of abrasive hardness on erosion.
Experiments have demonstrated that abrasive hardness has an important role in the target erosion effect. For example, TILLY [25] claimed that the erosion rate of a material is directly proportional to the 2.3 power of abrasive hardness. The effect of abrasive hardness on the erosion rate can also be determined using the ratio of abrasive hardness (Ha) to material hardness (Hm). When Ha/Hm>1, the erosion wear rate decreases markedly with the increase of abrasive hardness. On the other hand, when Ha/Hm<1, the erosion rate remains almost constant as abrasive hardness changes. Accordingly, abrasive impact is classified into hard and soft abrasive wear. That is, when Ha/Hm≥1.3-1.7, the wear of the target is irrelevant to the abrasive, thus corresponding to hard abrasive wear; and when Ha/Hm≤0.7-1.1, the material is almost not subject to wear [26]. However, all the above studies are based on static loading experiments. During the impingement of an abrasive air jet, the quasi-static and impact loads act jointly on the target. While eroding the target, the abrasive breaks into smaller pieces, which rebound at approximately 0.3 times their initial velocity [27]. This suggests that the impact kinetic energy of the abrasive not only causes target erosion, but also partially reflects and crushes the abrasive. Studies show that the changes in the particle size range of a hard abrasive before and after impact are smaller than those of a soft abrasive, the latter of which yields a more efficient erosion performance [18]. However, existing studies are all based on single-particle abrasives. An abrasive air jet, on the other hand, impinges the target in the form of an abrasive cluster. Its reflective abrasion has a secondary effect on the erosion of the target, which can affect the impact velocity of incident abrasive particles, thereby affecting the fragmentation degree and erosion effect of the abrasive. Moreover, unlike single-particle abrasive erosion experiments, the abrasive velocity of an abrasive cluster is difficult to determine. Abrasive velocity is affected by parameters such as air jet velocity, abrasive mass flow, particle size, and density [9]. Thus, appropriate experimental parameters are difficult to select. In addition, there has been no research on the mechanisms by which abrasive particle hardness influences the erosion effect. It has been proposed that the fragmentation degree of the abrasive particles reflects the conversion efficiency of the abrasive impact kinetic energy. Hard abrasives have a higher impact performance because they are not easily broken during target erosion, which results in a lower increase in free energy on the particle surface and more efficient energy conversion.
Hence, to clarify the influencing regularities of abrasive hardness on the erosion effect of abrasive air jets, this research involves the following objectives. The acceleration processes of abrasives with different hardness are analyzed numerically using the ANSYS Fluent software to obtain the air jet pressures of different abrasives at the same impact energy. On this basis, an abrasive air jet erosion test is conducted to comparatively analyze the variation regularities of particle size and surface area before and after erosion between various abrasives. The fracture energy required for abrasive crushing is analyzed, and the law by which abrasive hardness affects the erosion effect is clarified.
2 Determination of parameters for abrasive air jet erosion tests
2.1 Numerical simulation
The erosion velocity of an abrasive depends on its acceleration process. This process can be divided into three sections, namely the pipe, nozzle, and jet core sections. Among them, the nozzle and jet core are the main acceleration sections [28]. The gas jet velocity in the nozzle and jet core sections determines whether the abrasive can be accelerated sufficiently. A better nozzle structure enables the gas jet velocity field to fully develop so that there is a high conversion efficiency of jet energy. Studies have shown that the de Laval nozzle can better control the structure of a jet flow field, allowing for the full development of the velocity field within the nozzle and jet core sections and thereby adequately accelerating the abrasive [29, 30]. Abrasive acceleration is closely related to other parameters, such as particle size, density, and mass flow of the abrasive, aside from the jet flow-field structure. Within the same jet flow field, the acceleration processes of different abrasives also vary. To analyze the influence of abrasive hardness on the erosion effect, it is first necessary to ensure that the different abrasives used have the same impact kinetic energy, i.e., the same mass flow and velocity.
At present, abrasive velocity is analyzed mostly via experimental measurements and numerical calculations. Experimental measurements are mostly performed using noncontact or indirect methods, such as particle image velocimetry (PIV). Although the motion trajectory of the abrasive can be observed indirectly, the test results can only reflect the movement of abrasive particles under specific conditions and are thus unable to reveal the general regularity. Thus, in this study, the velocity field-distribution regularities of different types of abrasives in an air jet were simulated numerically. The velocity distributions of silicon carbide, brown aluminum oxide, garnet, and quartz sand in an air jet were calculated using Fluent to obtain the initial jet pressures of air jets with the same impact velocity at a target distance of 12 cm for these four types of abrasives under equal mass flow rate conditions. The parameters set for the four types of abrasives are listed in Table 1.
Table 1 Abrasive parameters

The de Laval nozzle was selected as the air jet nozzle because it has higher energy conversion efficiency than cone-convergent and cylindrical nozzles. The de Laval nozzle structure is shown in Figure 1. Based on this nozzle structure and the development characteristics of the free jet section, a physical model for numerical analysis was built. The parameters were set as follows: nozzle inlet straight section length of 6 mm, nozzle convergent section length of 2 mm, throat section length of 6 mm, divergent section length of 11.4 mm, nozzle inlet diameter of 4 mm, outlet diameter of 4.1 mm, free flow field dimensions of 200 mm×40 mm. A structured grid was generated with quadrilateral meshes. A total of 448944 meshes were generated. The inlet boundary was the pressure inlet, the outlet boundary was the pressure outlet, and the wall surface was a no-slip wall. As initial conditions, jet pressures varied for the different types of abrasives were set, and the inlet temperatures were all set to 300 K and the outlet pressures were all set to 0.1 MPa.

Figure 1 Nozzle structure parameters (Unit: mm):
Two numerical models (gas phase model and particle phase model) were included in the simulation. For the gas-phase flow field, the RNG k-ε turbulence model used in this study can simulate the high Reynolds number flow of the jets. The gas was assumed to be an ideal gas. The governing equations for the RNG k-ε turbulence model are [31]

 (1)
(1)

 (2)
(2)
where



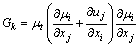 ;
;
 ;
;
ρ is density; k is the turbulent kinetic energy; ε is the dissipation rate of k; t is time; xi are Cartesian coordinates; ui and uj are the velocity components along the i and j directions, respectively; μ is gas viscosity; μt is eddy viscosity; Gk is the generation term of the turbulent kinetic energy k resulting from the mean velocity gradient; Gb is the generation term of the turbulent kinetic energy owing to buoyancy; YM is the effect of compressible turbulent pulsatile expansion on the total dissipation rate; αk and αε are the reciprocals of the effective Prandtl numbers for turbulent kinetic energy and dissipation rate, respectively; Prt is the turbulence Prandtl number; C1ε, C2ε and C3ε are empirical constants; gi is the component of gravitational acceleration in the i direction; φ is the thermal expansion coefficient; and a is the acoustic velocity.
The gas phase continuity equation is
 (3)
(3)
The gas phase Navier–Stokes equation is

 (4)
(4)
where εf is the gas volume fraction; ρf is gas density (kg/m3); t is time (s); is the gas velocity vector (m/s); P is pressure (kPa);
is the gas velocity vector (m/s); P is pressure (kPa);  is the fluid–particle interaction force (N); τf is the gas phase stress tensor; and
is the fluid–particle interaction force (N); τf is the gas phase stress tensor; and is the gravity acceleration vector (m/s2).
is the gravity acceleration vector (m/s2).
The discrete phase model (DPM) was applied to calculating the particle phase. The DPM of particle phase is given as
 (5)
(5)
where  is the drag force per unit particle mass and
is the drag force per unit particle mass and
 ;
;
 ;
;
Fx is an additional acceleration due to the Saffman lift force and the pressure gradient; μp is the particle velocity; μf is the velocity of the fluid; g is the acceleration of gravity; ρp is the density of the particle; dp is the diameter of the particle; CD is the drag coefficient; and Rep is the relative Reynolds number.
The different types of abrasives need to have the same impact kinetic energy for the same target distance according to the kinetic equation:
 (6)
(6)
where Jp is the impact energy; Qp is the mass flow of particles; t is erosion time.
Thus, the abrasives need to have an identical impact velocity under an equal mass flow rate. Owing to the different acceleration processes of the different types of abrasives considered, the jet pressures for accelerating the jets to the same velocity also vary. The DPM can be used to calculate the velocity of individual particles and the average velocity of particles. The impact energy is calculated using the average velocity per unit time to simplify the calculations. A reference impact energy value is required to calculate the air jet pressure when the impact energies of different abrasives are the same. Brown aluminum oxide is the most widely used abrasive in CBM research. The critical air jet pressure and mass flow are 5 MPa and 10 g/s, respectively [10, 11]. The average velocity calculated under these conditions was taken as the reference value, which was 105 m/s. Then, to obtain the air jet pressure of silicon carbide with an average velocity of 105 m/s and a mass flow of 10 g/s, the initial air jet pressure was continuously changed to calculate the average velocity of this abrasive and compare it with the reference value. When the two values were approximately equal, the corresponding pressure was regarded as optimal. The air jet pressures for garnet and quartz sand were calculated using the same method. The mesh number of the abrasives was 36, and the results are shown in Table 2. The impact energies shown in Table 2 were calculated with the unit time for the four types of abrasives being approximately equal and considering that the error is small enough to neglect.
Table 2 Jet pressures of different types of abrasives at same impact kinetic energy

Our calculations indicate that dense brown aluminum oxide requires a jet pressure of 5 MPa, whereas the less dense quartz sand only requires a jet pressure of 3.3 MPa. As shown in Figure 2, the abrasives are affected by the propagation regularities of the gas jet expansion and compression waves during the acceleration of the gas jet. The abrasives with higher velocity are all distributed around the jet axis. Under the influence of the jet boundary layer, a part of the abrasives is offset to the jet’s edge. There is a circular blank belt in the middle between the jet axis and the edge, which increases as density decreases.

Figure 2 Velocity distribution regularities of different types of abrasives
2.2 Experimental tests
To verify the reliability of the numerical simulation results, an I-Scan pressure testing system was used. The I-Scan system can be used to test the impact velocity and pressure distribution of air jets. The average velocity, pressure, and the changes over time of the impact area can be calculated via post-processing. The range of the I-Scan system used was 0-34.5 MPa, the sensor distribution density was 248 m-2, and the sample frequency was 0-100 Hz. This test system also concluded the high-pressure abrasive gas jet erosion experimental system used, which consisted of a high-pressure air compressor, a high-pressure gas cylinder, a digital pressure gauge, a pressure-control valve, an abrasive tank, a gate valve, and an operation box. The high-pressure air compressor had a maximum pressure of 40 MPa and a maximum air intake of 2 m3/min, whereas the high-pressure gas cylinder had a maximum allowable pressure of 40 MPa. These system devices were connected as shown in Figures 3 and 4. The nozzle used was a de Laval nozzle, whose structural parameters are shown in Figure 1. Before the experiments, high-pressure gas was stored in the high-pressure gas cylinder and the outlet pressure was adjusted with the pressure- regulating valve. The inlet pressure ranged in 0-40 MPa, whereas the outlet pressure ranged in 0- 25 MPa. With an adjustable outlet pressure accuracy of 0.05 MPa, the pressure-regulating valve could be used to accurately control jet pressure, thereby ensuring a constant jet pressure during the experiment in order to meet the experimental requirements. To control the mass flow rate of the abrasives, a high-pressure gate valve was installed below the abrasive tank. This gate was suitable for controlling the flow of solid particles under high-pressure conditions. Before the experiment, the gate valve scales corresponding to the mass flow of different abrasives were determined during calibration. The gas tank was filled with 30-MPa high-pressure air. A wear-resistant resin film was closely attached to the I-Scan sensor, which improves the erosion resistance of the sensor without affecting its measurement accuracy.
The test results are shown in Figure 5. The velocity distributions of the abrasive air jets calculated by the I-Scan system were similar to those of our numerical simulations. The jet axial velocities were higher than the boundary velocities. There were also blank areas between the axial and boundary regions, which decreased as density increased. The highest velocities for the silicon carbide, brown aluminum oxide, garnet, and quartz sand abrasives were 132, 127, 129 and 130 m/s, respectively. The results are in accordance with the numerical simulations, which indicates that the numerical model proposed in this study can effectively simulate the velocity distribution of abrasive air jets.

Figure 3 High-pressure abrasive air jet erosion system

Figure 4 Connection schematic of high-pressure abrasive air jet erosion system

Figure 5 Velocity contours of abrasive air jets tested using I-Scan system:
3 Experimental analysis on influence of abrasive hardness on erosion effect
3.1 Experimental scheme
Based on the calculations shown in Section 2, the jet and abrasive parameters to be used in the following experiment could be determined. The mesh number of the four kinds of abrasives used in experiment was 36, which was the same with numerical simulation. Limestone was used as the erosion target. To ensure that the mechanical and physical properties of the eroded limestone were identical, f 50×100 rock samples were prepared by coring the same rock mass (as shown in Figure 6). Two rock samples were selected and their mechanical properties were tested using an MTS device, and the results are presented in Table 3. Before performing each of the erosion experiments, the gas pressure in the gas tank was increased to over 15 MPa, the abrasive tank was filled with the corresponding abrasive, and the gate valve position was adjusted to ensure that the mass flow met the required experimental conditions.

Figure 6 Limestone samples
Table 3 Mechanical properties of limestone samples

3.2 Results analysis
3.2.1 Abrasive morphology microanalysis before and after erosion
The four types of abrasives were observed before and after erosion under an electron microscope. Before erosion, the four abrasives had a similar particle size with sharp edges and regular shapes. For example, silicon carbide was regular columnar polyhedral, whereas quartz sand was almost spherical (Figures 7(a)-(d)). After erosion, the abrasives were damaged, and all four abrasives had broken into abrasive particles of different sizes with differing failure modes, as shown in Figures 7(a′)-(d′). After being damaged, the larger particles of silicon carbide exhibited obtuse edges, whereas the smaller particles had sharp edges. Brown aluminum oxide also exhibited the same characteristics, but with larger particle sizes than silicon carbide after being damaged. As for garnet and quartz sand, the edges were sharp after being damaged regardless of particle size. The post-failure particle size of brown aluminum oxide was smaller than that of silicon carbide but larger than that of garnet.
The main cause of the morphological inconsistencies between abrasives with different hardness after erosion damage was the action mechanism of abrasives and limestone. The limestone erosion process by abrasives occurs as follows. When high-speed abrasives contact the limestone surface, they exert a concentrated load on it, pressing into the surface to form cracks. Cracks develop inward in the limestone from the four corners of indentation. When the cracks cross each other or propagate to the surface, the microscopic rupture of limestone is induced, causing surface wear. Aside from causing the surface wear of limestone, these concentrated loads also lead to the expansion of cracks and pores in the rock’s interior. Because the abrasives are brittle, the cracks and pores inside the abrasive particles expand under reactive-force action. When these cracks penetrate the abrasive particles, brittle fracture occurs, which in turn causes them to break into several differently sized particles owing to variations in the distribution regularity of primary fractures and the modes of their molecular arrangement.
The abrasive particles get reflected after impacting on the limestone. They wear the limestone-erosion pit surface during this reflection process, thereby resulting in an enlarged erosion pit diameter. The erosion angle of the reflected abrasive differs from the vertical impact angle of the incident abrasive. The incidence angle between the reflected abrasive and the limestone surface is small, and the wear forms pear grooves. The reflected abrasive wears the limestone surface in the form of shear stress. During the wear process, large-diameter abrasive particles first contact the limestone surface owing to its large contact area. While wearing the limestone surface, the sharpness of the edges of the abrasive particles undergoes changes. The Mohs hardness of limestone is 3. The hardness ratios of quartz sand and garnet to limestone are between 2.3 and 2.6, whereas those of brown aluminum oxide and silicon carbide to limestone are over 3. According to the abrasive hardness classification under static load conditions, they all belong to the hard abrasive wear category. However, as can be seen from the micrographs, the larger particles of quartz sand and garnet had obtuse edges. This suggests that the abrasives themselves are worn when wearing the limestone because they are subjected to the action of shear stress. In contrast, the larger particles of brown aluminum oxide and silicon carbide exhibited obtuse edges, indicating that the shear stress in these experiments did not cause wear on these abrasives. This suggests that the classification of abrasive hardness under static load conditions is unable to adequately explain the abrasive wear observed under equal impact conditions. Using the same definition under equal impact conditions, the observed effect is due to soft abrasive impact when Ha/Hm<2.6 and hard abrasive impact when Ha/Hm>3.

Figure 7 Comparison of abrasives before (a-d) and after erosion (a′-d′):
3.2.2 Analysis of abrasive particle size distribution regularities after erosion
The particle sizes of the eroded abrasive particles were analyzed using a laser particle sizer. The cumulative volume percentages of the four abrasives are shown in Figure 8. It is clear that the abrasives undergo volumetric fracture after the erosion of limestone and are crushed into multiple particles with smaller sizes. Abrasives with different hardness values exhibited varying particle sizes and total particle numbers after being crushed. Harder abrasives, such as silicon carbide, exhibited a particle size distribution between 24 and 500 μm and a particle diameter of 211 μm when the volume is accumulated to 63.2% of the total volume. Softer abrasives, such as quartz sand, exhibited a particle size distribution of 4.5-240 μm and a particle diameter of 76 μm under the same conditions as mentioned above. Abrasives with lower hardness are thus more prone to suffering damage during erosion than those with higher hardness, and their after-failure particle size is also smaller. To clarify the relationship between abrasive hardness and fragmentation degree, the distribution characteristics of the abrasive particle sizes were analyzed. From the regularities of the cumulative volume percentage distribution, it can be seen that particle size distribution basically follows Weibull distribution. Thus, the Weibull distribution function was used to describe the distribution regularities of particle size, as follows [32, 33]:
 (7)
(7)
where V is the proportion of abrasives with a particle size not greater than d after erosion crushing to the total abrasive amount and d0 is the particle diameter when the volume is accumulated to 63.2% of the total volume, which is a parameter for characterizing the degree of fragmentation. β is the shape parameter of the Weibull function, which represents the crushing characteristic index of abrasives.

Figure 8 Cumulative volume percentages of abrasives after erosion
For an easier analysis of the distribution regularities of the abrasive particle sizes after crushing, Eq. (7) was logarithmically transformed. Thus, the particle-size distribution function of the abrasives after crushing becomes
 (8)
(8)
where F(d) is the mass cumulative distribution function of the abrasives with a crushed particle size not greater than d.
According to the particle-size distribution function of the crushed abrasives, the distributions of particle size for the abrasives with different hardness after impact were fitted using the least squares error method. Figure 9 shows the fitted curves. The correlation coefficients (R2) of the four types of abrasives were all above 0.98, suggesting that the particle-size distributions of the abrasives followed a Weibull distribution after impact crushing. The fitted Weibull functions are presented in Table 4. The crushing characteristic index β of the abrasives was calculated using the fitted functions. The value of β varied among the abrasives with different hardness. Quartz sand, which has a low hardness, exhibited a β value of 1.98, whereas the harder silicon carbide abrasive exhibited a β value of 2.11. Through data fitting, β was found to be in a quadratic relation with abrasive hardness, as shown in Figure 10. The relational expression is
 ,
,
 (9)
(9)
where Ha is the abrasive hardness.
Using the relationship established between the crushing characteristic index and the hardness of abrasives, the Weibull distribution model of particle size for abrasives of different hardness after impact could be determined, thereby clarifying the particle-size distribution regularities of the various abrasives after impact.

Figure 9 Particle size distributions after abrasive impact crushing:
Table 4 Fitted functions for cumulative volume distribution

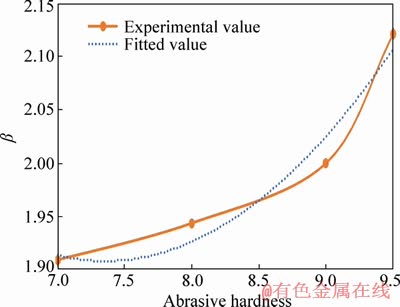
Figure 10 Relationship between abrasive hardness and crushing characteristic index β
3.2.3 Analysis of influence of abrasive hardness on limestone erosion effects
A critical engineering parameter for abrasive gas jets used for drilling CBM wells and improving CBM recovery efficiency is erosion depth. Erosion depth is significantly affected by abrasive hardness and is associated with the impact kinetic energy of the abrasive jet. However, currently available research fails to consider the jet impact kinetic energy and abrasive hardness separately, primarily because the impact velocity of abrasives is difficult to calculate. Based on equal impact kinetic energy conditions, erosion tests were carried out using abrasives with different hardness in order to clarify the effect of abrasive hardness on erosion depth when using abrasive air jets.
When an abrasive air jet acts on a rock mass, macroscopic failure manifests by the formation of erosion pits and macroscopic cracks [34-37]. The energy responsible for the failure of the rock mass arises from the jet energy Ew, which propagates in the rock mass as a stress wave. In addition, the jet energy is also the source of the rebound kinetic energy Er (including the increase in abrasive surface energy) of the abrasive jet. Ew can be decomposed into the splash kinetic energy Ee of rock debris, the crushing energy Ec, which consists of the new surface area energy of fragments and the surface energy of new cracks, and miscellaneous energies Em, such as radiant energy, thermal energy, and sound waves [38-41]. The proportion at which the impact energy of the abrasive jet is converted into stress wave energy determines its rock-breaking effects. Our experimental results show that the erosion depth and erosion volume were both the highest for silicon carbide (33.5 mm and 15.15 mm3, respectively), and both the lowest for quartz sand (14.0 mm and 3.70 mm3, respectively), as shown in Table 5 and Figure 11. Erosion depth and volume increased with the hardness of the abrasives, indicating that harder abrasives have a higher conversion rate of impact energy into stress wave energy and a smaller proportion of impact energy is converted into rebound kinetic energy.
Table 5 Abrasive hardness and erosion parameters


Figure 11 Limestone samples after erosion
Abrasives are subjected to reactive forces after impacting on their target. This reactive force also propagates inside the abrasives in the form of stress waves. During propagation in the abrasive particles, a part of these stress waves is reflected and superimposed on the subsequent wave, accumulating energy when passing through the primary cracks and pores; the other part diffracts, continues to propagate deeply inward the particles, and is reflected and superimposed at other cracks, accumulating energy. When the accumulated energy is greater than the sum of the shear strain energy and volumetric strain energy of the particles, the abrasive particles undergo yield failure [42-47]. Therefore, the damage degree of abrasive particles depends on their own mechanical properties under equal impact velocity conditions. For example, the hardness of quartz sand is lower than that of silicon carbide. Despite the similar density of quartz sand and silicon carbide, the shear strength of quartz sand is lower owing to its varying molecular arrangements. At an equal impact velocity, the damage degree of quartz sand is relatively higher. According to the analysis presented in the previous section, it can be seen that the post-failure particle size of quartz sand is smaller than that of silicon carbide; that is, the post-failure increase in surface energy is higher for quartz sand than for silicon carbide. Therefore, quartz sand uses more energy for increasing the post-failure surface energy during the erosion of limestone and uses less energy for impacting the target rocks. To intuitively represent the relationship between abrasive hardness and erosion effect, data fitting was performed to find a quadratic relation between abrasive hardness and erosion depth, as shown in Figure 12. The relational expression found was

 (10)
(10)

Figure 12 Relationship between crushing abrasive hardness of abrasives and erosion depth
4 Influence of abrasive hardness on energy consumption of abrasive broken
Through the analysis presented in Section 3, it can be concluded that the key to the influence of hardness on the erosion effect of an abrasive gas jet lies in the failure characteristics of the abrasives themselves during the erosion process. After crushing, the surface area of the abrasives increases. The smaller the particle size after failure, the larger the required surface energy and the lower the proportion of energy used for the erosion of the target, in turn resulting in shallower erosion depths. Clarifying the surface-energy conversion rate of abrasives with different hardness during target erosion is key for analyzing the influence of abrasive hardness on erosion effect.
In order to accurately calculate the energy dissipated due to the increase of surface area caused by abrasive crushing, the contact angles of four abrasives were tested. The surface tension was calculated based on the contact angle. Then, the energy consumed in crushing of the four abrasive materials was calculated according to the specific surface area obtained from particle size test.
4.1 Contact angle of abrasive
Theta Optical Tensiometer produced by Biolin Scientific was used to measure the contact angle of the four abrasives. In order to measure the contact angle more accurately, natural materials used to make abrasive were selected for the measured samples, as shown in Figure 13. One side of the sample was polished to measure the contact angle. The selected liquid for measurement was distilled water. The measurement results are shown in Figure 14.
4.2 Energy consumption of abrasive broken
The surface tension of abrasive could be calculated by the Berthebt method [48]:
 (11)
(11)
where γsg is surface tension at the gas/solid interface; γlg is surface tension at the gas/liquid interface; θ is contact angle.
The energy required to increase the surface of abrasive crushing is [49]
 (12)
(12)
where Es is the energy required to produce a new fracture surface; σ is compressive strength of abrasive; E is elasticity modulus of abrasive; V is volume; A is the fracture area generated during abrasive crushing.
The specific surface area after the crushing of four kinds of abrasives is tested by the laser particle size meter, and the energy consumed by the new surface after the crushing of abrasive per unit mass is calculated according to Eq. (12), as shown in Table 6.

Figure 13 Raw material of four kind abrasives:

Figure 14 Contact angle of four kind abrasives:
Table 6 Surface tension and surface energy

The four types of abrasives used all exhibited a surface area of approximately 3.97 m2/kg before erosion. After erosion, their surface area increased owing to the decreased particle size. Among them, silicon carbide exhibited the least increase in surface area and surface energy, which were 17.75 m2/kg and 1.87 J, respectively, whereas quartz sand exhibited the greatest increase, with specific values of 35.00 m2/kg and 4.51 J, respectively. The ratio of the increase in abrasive surface energy to the initial impact kinetic energy is defined as the surface energy consumption. It can be derived that the energy consumption of the surface energy also decreases gradually as abrasive hardness increases. The surface energy consumption was 8.2% for quartz sand, whereas it was only 3.4% for silicon carbide. Small surface energy consumption indicates that the initial kinetic energy of the abrasive air jet particles is largely transformed into rock impact energy, meaning that the resulting erosion depth and volume are both large. By analytically fitting the relationship between abrasive hardness and surface energy (as shown in Figure 15), the two factors were found to be quadratically related as follows:

 (13)
(13)
The erosion pit depth of silicon carbide was 2.39 times, 1.46 times, and 1.19 times that of quartz sand, garnet, and brown aluminum oxide, respectively. Additionally, the surface energy of the eroded quartz sand was 2.40 times, 1.91 times, and 1.35 times that of silicon carbide, brown aluminum oxide, and garnet, respectively. This comparison reveals that increases in erosion depth and surface energy consumption were basically identical. That is, abrasive hardness is the primary factor influencing the erosion effect.

Figure 15 Relationship between abrasive hardness and surface energy consumption
5 Conclusions
Limestone erosion experiments were conducted using a high-pressure abrasive gas jet erosion test system. After rock erosion, the abrasive particles undergo brittle fracture, and harder abrasives exhibit larger particle sizes after suffering damage. During the reflection process, the abrasives wear the limestone surface through shear stress, and the softer abrasives undergo wear themselves. For example, the edges of quartz sand and garnet particles become obtuse, whereas harder abrasives, such as silicon carbide and brown aluminum oxide, show no signs wear. That is, under equal impact conditions, the erosion effect can be considered a soft abrasive impact when Ha/Hm<2.6 and a hard abrasive impact when Ha/Hm>3.
The particle size distributions of the abrasives after erosion follow the Weibull distribution model. The shape parameter β in Weibull distributions is defined as the abrasive crushing characteristic index, which was found to be quadratically related to abrasive hardness. Abrasive hardness and erosion depth are in a quadratic relationship as well. The increase in the surface energy of the abrasives after erosion and breakage is an important influencing factor on the erosion effect. Abrasive hardness and surface energy were found to share a quadratic relationship; that is, harder abrasives exhibit a smaller surface energy consumption. Moreover, increases in erosion depth and surface energy consumption were found to be basically identical. Thus, abrasive hardness was identified as the primary factor affecting the erosion effect under equal impact kinetic energy conditions.
References
[1] LU Yi-yu, LIU Yong, LI Xiao-hong, KANG Yong. A new method of drilling long boreholes in low permeability coal by improving its permeability [J]. International Journal of Coal Geology, 2010, 84(2): 94-102.
[2] LIU Yong, XIA Bin-wei, LIU Xiao-tian. A novel method of orienting hydraulic fractures in coal mines and its mechanism of intensified conduction [J]. Journal of Natural Gas Science and Engineering, 2015, 27: 190-199.
[3] FANG Jun, WANG Yan-bin, GAO De-li. On the collapse resistance of multilayer cemented casing in directional well under anisotropic formation [J]. Journal of Natural Gas Science and Engineering, 2015, 26: 409-418.
[4] LIU Chun, ZHOU Fu-bao, YANG Kang-kang. Failure analysis of borehole liners in soft coal seam for gas drainage [J]. Engineering Failure Analysis, 2014, 42: 274-283.
[5] LU Yi-yu, HUANG Fei, LIU Xiao-chuan, AO Xiang. On the failure pattern of sandstone impacted by high-velocity water jet [J]. International Journal of Impact Engineering, 2015, 76: 67-74.
[6] FAN J M, WANG C Y, WANG J. Modelling the erosion rate in micro abrasive air jet machining of glasses [J]. Wear, 2009, 266(9): 968-974.
[7] HEJJAJI A, ZITOUNE R, CROUZEIX L, LE ROUX S, COLLOMBET F. Surface and machining induced damage characterization of abrasive water jet milled carbon/epoxy composite specimens and their impact on tensile behavior [J]. Wear, 2017, 376-377: 1356-1364.
[8] JAFAR R H M, NOURAEI H, EMAMIFAR M, PAPINI M, SPELT J K. Erosion modeling in abrasive slurry jet micro-machining of brittle materials [J]. Journal of Manufacturing Processes, 2015, 17(1): 127-140.
[9] KALIAZINE A, ESLAMIAN M, TRAN H N. On the failure of a brittle material by high velocity gas jet impact [J]. International Journal of Impact Engineering, 2010, 37(2): 131-140.
[10] LIU Yong, ZHANG Juan, WEI Jian-ping, LIU Xiao-tian. Optimum structure of a laval nozzle for an abrasive air jet based on nozzle pressure ratio [J]. Powder Technology, 2020, 364(3): 343-362.
[11] WEN Zhi-hui, LIU Yong. Experimental research into the effects of abrasive characteristics on abrasive gas jet coal-breaking performance [J]. International Journal of Heat and Technology, 2017, 35: 32-36.
[12] HUANG Fei, LI Shu-qing, ZHAO Yan-lin, LIU Yong. Study on lateral jetting range during an arc-curved jet impacting nonplanar solid surfaces [J]. Journal of Fluids Engineering-Transactions of the Asme, 2018, 140(10): 101201.
[13] CHEN Shi-kuo, YANG Tian-hong, RANJITH P G, WEI Chen-hui. Mechanism of the two-phase flow model for water and gas based on adsorption and desorption in fractured coal and rock [J]. Rock Mechanics and Rock Engineering, 2017, 50(3): 571-586.
[14] SUN Jun-long, LIU Chang-xia, TIAN Jin, FENG Bao-fu. Erosion behavior of B4C based ceramic nozzles by abrasive air-jet [J]. Ceramics International, 2012, 38(8): 6599-6605.
[15] ESLAMIAN M, POPHALI A, BUSSMANN M, TRAN H N. Breakup of brittle deposits by supersonic air jet: The effects of varying jet and deposit characteristics [J]. International Journal of Impact Engineering, 2009, 36(2): 199-209.
[16] PETASYUK G A. System and criterial method of the identification and quantitative estimation of the geometrical shape of the abrasive powder grain projection [J]. Powder Technology, 2014, 264: 78-85.
[17] FOWLER G, PASHBY I R, SHIPWAY P H. The effect of particle hardness and shape when abrasive water jet milling titanium alloy Ti6Al4V [J]. Wear, 2009, 266(7): 613-620.
[18] TREVISIOL C, JOURANI A, BOUVIER S. Effect of hardness, microstructure, normal load and abrasive size on friction and on wear behaviour of 35NCD16 steel [J]. Wear, 2017, 388-389: 101-111.
[19] BABU P S, BASU B, SUNDARARAJAN G. The influence of erodent hardness on the erosion behavior of detonation sprayed WC-12Co coatings [J]. Wear, 2011, 270(11): 903-91.
[20] ORECNY M, BURSAK M, SEBEK M, FALAT L. Influence of hardness, matrix and carbides in combination with nitridation on abrasive wear resistance of X210Cr12 tool steel [J]. Metals, 2016, 6(10): 236.
[21] APONTE R D, TERAN L A, LADINO J A, LARRAHONDO F, CORONADO J J, RODRIGUEZ S A. Computational study of the particle size effect on a jet erosion wear device [J]. Wear, 2017, 374-375: 97-103.
[22] LI H Z, LEE A, FAN J, YEOH G H, WANG J. On DEM-CFD study of the dynamic characteristics of high speed micro-abrasive air jet [J]. Powder Technology, 2014, 267: 161-179.
[23] BAHADUR S, BADRUDDIN R. Erodent particle characterization and the effect of particle size and shape on erosion [J]. Wear, 1990, 138(1, 2): 189-208.
[24] ARABNEJAD H, MANSOURI A, SHIRAZI S A, MCLAURY B S. Abrasion erosion modeling in particulate flow [J]. Wear, 2017, 376-377: 1194-1199.
[25] TILLY G P. A two stage mechanism of ductile erosion [J]. Wear, 1973, 23(1): 87-96.
[26] KHRUSCHOV M M. Principles of abrasive wear [J]. Wear, 1974, 28(1): 69-88.
[27] GAITANAROS S, KYRIAKIDES S. On the effect of relative density on the crushing and energy absorption of open-cell foams under impact [J]. International Journal of Impact Engineering, 2015, 82: 3-13.
[28] JUNKAR M, JURISEVIC B, FAJDIGA M, GRAH M. Finite element analysis of single-particle impact in abrasive water jet machining [J]. International Journal of Impact Engineering, 2006, 32(7): 1095-1112.
[29] FAN J M , WANG C Y , WANG J. Modelling the erosion rate in micro abrasive air jet machining of glasses [J]. Wear, 2009, 266(9): 968-974.
[30] LONG Xin-ping, RUAN Xiao-feng, LIU Qi, CHEN Zheng-wen, XUE Sheng-xiong, WU Zi-quan. Numerical investigation on the internal flow and the particle movement in the abrasive waterjet nozzle [J]. Powder Technology, 2017, 314: 635-640.
[31] KOUTSOURAKIS N, BARTZIS J G, MARKATOS N C. Evaluation of reynolds stress, k-epsilon and RNG k-epsilon turbulence models in street canyon flows using various experimental datasets [J]. Environmental Fluid Mechanics, 2012, 12(4): 379-403.
[32] XU Yong-feng, SONG Dang-qing, CHU Fei-fei. Approach to the Weibull modulus based on fractal fragmentation of particles [J]. Powder Technology, 2016, 292: 99-107.
[33] BROUWERS H J H. Packing fraction of particles with a Weibull size distribution [J]. Physical Review E, 2016, 94(1): 012905.
[34] LIU Yong, ZHANG Tao, LIU Xiao-tian. Analysis of the stress wave effect during coal breakage by a high-pressure abrasive air jet [J]. Advances in Mechanical Engineering, 2018, 10(6): 1-11. DOI: 10. 1177/1687814018782302.
[35] LIU Yong, ZHANG Hui-dong, RANJITH P G, WEI Jian-ping, LIU Xiao-tian. Wear mechanism of abrasive gas jet erosion on a rock and the effect of abrasive hardness on it [J]. Geofluids, 2019, 2019: 1-14. DOI: 10.1155/2019/ 4125363.
[36] RANJITH P G, LIU Yong, WEI Jian-ping, LIU Xiao-tian. Effect of abrasive mass flow on the abrasive acceleration and erosion rates of abrasive gas jets [J]. Rock Mechanics and Rock Engineering, 2019, 52: 3085-3102. DOI: 10.1007/ s00603-019-01746-3.
[37] LIU Yong, ZHANG Juan, ZHANG Tao, ZHANG Hui-dong . Optimal nozzle structure for an abrasive gas jet for rock breakage [J]. Geofluids, 2018, 2018: 1-14. DOI: 10.1155/ 2018/9457178.
[38] LI Xi-bing, WANG Shi-ming, WENG Lei, HUANG Lin-qi, ZHOU Tao, ZHOU Jian. Damage constitutive model of different age concretes under impact load [J]. Journal of Central South University, 2015, 22(2): 693-700. DOI: 10.1007/ s11771-015- 2527-0.
[39] LIU Xi-ling, LI Xi-bing, HONG Liang, YIN Tu-bing, RAO Ming. Acoustic emission characteristics of rock under impact loading [J]. Journal of Central South University, 2015, 22(9): 3571-3577. DOI: 10.1007/s11771-015-2897-8.
[40] LIU Ke-wei, LI Xiao-han, LI Xi-bing, YAO Zhi-hua, SHU Zong-xian, YUAN Ming-hua. Characteristics and mechanisms of strain waves generated in rock by cylindrical explosive charges [J]. Journal of Central South University, 2016, 23(11): 2951-2957. DOI: 10.1007/s11771-016- 3359-7.
[41] YIN Tu-bing, WANG Pin, LI Xi-bing, SHU Rong-hua, YE Zhou-yuan. Effects of thermal treatment on physical and mechanical characteristics of coal rock [J]. Journal of Central South University, 2016, 23(9): 2336-2345. DOI: 10.1007/ s11771-016-3292-9.
[42] JU Yang, YANG Yong-ming, MAO Yan-zhe, LIU Hong-bin, WANG Hui-jie. Laboratory investigation on mechanisms of stress wave propagations in porous media [J]. Science in China Series E-Technological Sciences, 2009, 52: 1374-1389.
[43] JU Yang, WANG Hui-jie, YANG Yong-ming, HU Qin-ang, PENG Rui-dong. Numerical simulation of mechanisms of deformation, failure and energy dissipation in porous rock media subjected to wave stresses [J]. Science China- Technological Sciences, 2010, 53: 1098-1113.
[44] JU Yang, SUDAK L, XIE He-ping. Study on stress wave propagation in fractured rocks with fractal joint surfaces [J]. International Journal of Solids and Structures, 2007, 44(13): 4256-4271.
[45] GAO Zhi-yong, SUN Wei, HU Yue-hua. Mineral cleavage nature and surface energy: Anisotropic surface broken bonds consideration [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(9): 2930-2937.
[46] JIANG Xiao-bao, XIAO Bei-bei, GU Xiao-yan, ZHANG Xing-hua. Modeling the effects of size and surface broken bond on surface energy of nanocrystals [J]. Thin Solid Films, 2017, 640: 67-72.
[47] STAGONAS D, WARBRICK D, MULLER G, MAGAGNA D. Surface tension effects on energy dissipation by small scale, experimental breaking waves [J]. Coastal Engineering, 2011, 58(9): 826-836.
[48] POCIUS A V, DILLARD D A. Adhesion science and engineering: surfaces, chemistry and applications [M]. Elsevier, 2002.
[49] MYSHKIN N, KOVALEV A. Adhesion and surface forces in polymer tribology—A review [J]. Friction, 2018, 6(2): 143- 155.
(Edited by YANG Hua)
中文导读
磨料硬度对磨料气体射流冲蚀磨损的影响
摘要:为了研究磨料硬度对冲蚀效果的影响,开展了相同冲击能量条件下磨料射流冲蚀实验。并通过对比分析冲坑深度,明确了磨料硬度与冲蚀效果之间的关系。研究得出,在相同质量流量、相同粒径条件下,为获得相同冲击能量,密度大的磨料需要较大压力,与硬度无关。磨料粒子冲蚀破坏后,粒径成Weibull分布,且通过最小平方差法得出了四种磨料的形状参数β和Weibull分布函数,其中,β与磨料硬度成二次方关系。通过冲蚀实验,得出磨料硬度与冲蚀深度呈二次方关系。通过计算磨料冲蚀破碎后增加的表面能,得出磨料硬度和表面能成二次方关系,且冲蚀深度和表面能耗能的增幅基本相同。综上所述,当磨料硬度(Ha)和材料硬度(Hm)的比值<2.6时,属于软磨料冲击;当Ha/Hm>3时,属于硬磨料冲击。
关键词:磨料气体射流;磨料硬度;岩石磨损;磨料粒径分布;煤层气
Foundation item: Projects(51704096, 51574112) supported by the National Natural Science Foundation of China; Project(192102310236) supported by the Key Scientific and Technological Project of Henan Province, China; Project(2019M662496) supported by Postdoctoral Science Foundation of China; Project(2017YFC0804209) supported by the National Key Research and Development Program of China; Project(J2018-4) supported by the Science Research Funds for the Universities of Henan Province, China
Received date: 2019-06-11; Accepted date: 2019-12-10
Corresponding author: WEI Jian-ping, PhD, Professor; Tel: +86-391-3986860; E-mail: weijianping@hpu.edu.cn; ORCID: 0000-0002- 5140-8204
Abstract: To make clear the influence of abrasive hardness on the erosion effect, the erosion experiments of abrasive air jet with the same impact energy were carried out. The influence of abrasive hardness on the erosion effect is clarified by comparing the different erosion depths. The main conclusions are as follows. Under the same mass flow rate and mesh number, the abrasive with a higher density needs greater pressure irrespective of hardness. After erosion damage, the abrasive size exhibits a Weibull distribution. The shape parameter β and Weibull distribution function of four types of abrasives are derived by the least squares method; moreover, β is found to have a quadratic relation with abrasive hardness. The results of the erosion experiments show that abrasive hardness and erosion depth are quadratically related. By calculating the increase in surface energy after abrasive erosion crushing, it is found that abrasive hardness has a quadratic relation with surface energy and that the increases in erosion depth and surface energy consumption are basically identical. In conclusion, the effect is a soft abrasive impact when the ratio of abrasive hardness (Ha) to the material hardness (Hm) is <2.6, and it is a hard abrasive impact when Ha/Hm >3.


