基于动力学分析的深海履带式采矿车行走打滑控制

韩庆珏^{1, 2}，刘少军^{1, 2}

(1. 中南大学 机电工程学院，湖南 长沙， 410083；

2. 深海矿产资源开发利用技术国家重点实验室，湖南 长沙，410012)

摘 要：

底海泥特性的基础上，利用膨润土模拟海泥，得到深海履带式采矿车牵引力和打滑率之间的关系。牵引力随打滑率增加而急剧减小，最终稳定在30 kN。通过对推土阻力、压实阻力、转弯阻力、水阻力的理论分析，建立履带式采矿车的动力学模型，提出了采矿车直线行走时打滑率i应≤20%的控制要求，并设计带模糊PID控制器的打滑率控制系统。利用Simulink软件，对控制系统进行仿真。仿真结果表明，所设计的打滑控制系统能够满足深海履带式采矿车行走控制要求，打滑率控制响应速度快、稳态性好，保证采矿车良好的动力性能。

关键词：

深海；履带式采矿车；打滑率；打滑控制；

中图分类号：TP242          文献标志码：A         文章编号：1672-7207(2013)08-3166-07

Slip control of deep sea tracked miner based on dynamic analysis

HAN Qingjue^{1, 2}, LIU Shaojun^{1, 2}

(1. College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;

2. National Key Laboratory of Development and Utilization of Deep-Sea Mineral Resource, Changsha 410012, China)

Abstract: Based on the analysis of the characteristic of the surface soil on the deep-sea bed, the relationship of the traction force and slip rate of the deep sea tracked miner is obtained. As the slip rate increases, the traction force decreases sharply. Also, the dynamic model of the tracked miner is established taking the bulldozing resistance, compaction resistance, steering resistance and water resistance in account. More importantly, a slip rate control system with a fuzzy PID controller is designed. By using Simulink software, a series of simulations are carried out to test the controller. As shown in the results, the slip rate controller is of fast and stable response, therefore, the validity of the controller is confirmed and can meet the control requirement, which is no more than 20%, and the dynamic performance of the deep sea tracked miner is ensured.

Key words: deep sea; tracked miner; slip rate; slip control

履带式行走机构因其自身固有的结构特点经常被广泛应用在军事、农业以及采矿等特殊路面环境领域^[1]。对于深海6 km多金属结核及钴结壳采矿领域而言，德国、印度、韩国、中国等众多国家，相继研制出了包含海底履带式采矿车的深海采矿系统。深海采矿的工作环境极为特殊。深海底海泥的力学特性直接影响到采矿车的行走性能。Zvi等^[1]对于履带车辆进行了理论建模和分析，但此模型仅适应于一般陆地，对于深海底特殊复杂环境下的履带车辆行驶力学的研究缺乏研究。针对软路面车辆行驶地面力学，Bekker^[2]提出确定剪切应力与剪切位移之间关系的实验方法；德国的Schulte等^[3]通过模拟海泥的沉陷和剪切实验，获得了剪切应力与剪切位移之间的关系；中南大学的李力等^[4]利用膨润土模拟我国深海矿区海泥特性，通过实验得到了我国深海表层海泥的剪切应力和位移关系。上述研究着重于履带驱动力和打滑之间的关系，对于深海履带采矿车行走过程中遇到的阻力问题未过多涉及。采矿车在行走过程中会受到来自海底沉积物的压实阻力、推土阻力、转弯阻力以及水动力和与之相连的输送软管等作用力的影响。这些阻力在深海履带式采矿车行走过程动力学分析研究中是极其重要的，这也是本文研究的重点之一。深海履带式采矿车的行走动力是通过履带相对地面打滑产生的剪切力获得的，打滑率直接影响到采矿车的行驶性能。传统陆地车辆的打滑控制方法主要有逻辑门法、PID控制法、模糊控制法以及滑模控制法^[5-6]；Herzog等^[7]对于深海环境下履带车辆打滑控制进行了实验研究，缺乏一定的理论分析。本文作者对深海履带式采矿车行走过程中打滑率进行了控制研究，通过模拟海泥的特性，结合我国深海表层海泥的剪切应力与位移之间的关系，得到了深海履带式采矿车牵引力与打滑之间的关系；通过对深海履带式采矿车行走过程的动力学分析提出采矿车打滑率的控制要求(i≤20%)，并设计了模糊PID控制系统，对打滑率进行控制。仿真结果表明，采矿车行走过程打滑率可以满足控制要求，确保了深海特殊环境下履带式采矿车的行驶性能。

1  采矿车地面力学特性研究

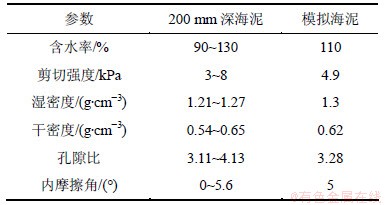
我国深海履带式采矿车行走时履带齿达到200 mm深的海泥层。为了模拟该层海泥的土力学特性，选取膨润土和水以一定的比例混合作为模拟海泥。表1所示为深海海底200 mm深海泥与模拟海泥的物理力学特性。

表1  200 mm深海泥与模拟海泥力学特性

Table 1  Parameters of surface soil under 200 mm deep-sea bed and simulating soil

根据Wong^[8]的车辆地面力学理论，土壤所提供的驱动力为：

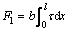              (1)

其中：F₁为土壤驱动力；b为履带宽度；l为履带接地长；τ为土壤剪切强度；x为接触点履带前端距离。

李力等^[4]通过实验获得了模拟海泥剪切应力与位移的关系表达式：

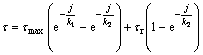        (2)

其中：τ为水平剪切应力；j为履带前端接触点距离的剪切位移，j=ix，i为打滑率；τ_max为最大剪切应力；τ_r为残余剪切应力；k₁=55；k₂=3。

由式(1)和(2)可以得到深海履带式采矿车履带总牵引力的计算式为：

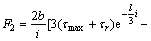
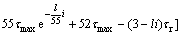       (3)

式中：F₂为履带总牵引力；取模拟海泥最大剪切应力τ_max=4.9 kPa，残余剪切应力τ_r=1.4 kPa，同时，根据我国1 000 m海试系统深海履带采矿车的设计参数(见表2)，可以得到深海采矿车履带总牵引力计算式为：

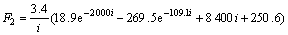(4)

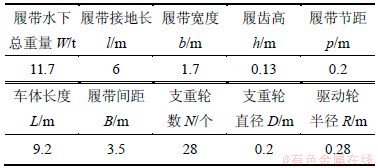
表2  海试系统采矿车主要设计参数

Table 2  Design parameters of miner

由式(4)可以绘制得到深海履带式采矿车履带总牵引力与打滑率之间的关系曲线。

从图1可知：当模拟深海底沉积物剪切强度为4.9 kPa时，采矿车的履带牵引力随着打滑率的增加而急剧减小，当打滑率大于20%时，牵引力基本稳定在30 kN附近。为使采矿车在深海软底质环境行驶过程中具有良好的动力性能，需要对采矿车进行动力学分析，并对其行走过程的打滑率进行控制。

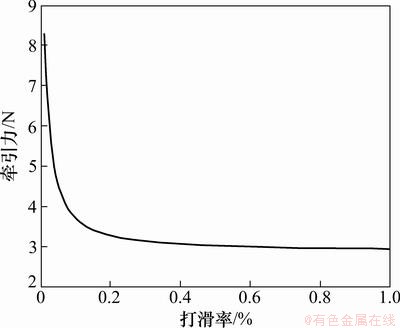
图1  牵引力与打滑率的关系

Fig. 1  Relationship between tractive force and slip rate

2  动力学模型

深海履带式采矿车采用履带自行式。行走机构包括履带、履带架、驱动轮、张紧轮与张紧装置、支重轮、拖链轮、动力装置等，用于载运集矿机构在海底自动行走作业。2条履带分别选用液压马达驱动，利用速度差实现采矿车转向。

深海履带式采矿车在海底直行过程中，其单侧履带的动力学方程为：

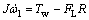             (5)

         (6)

式中：J为履带驱动轮相对于转轴的转动惯量；ω_l为履带的转动角速度；T_w为单侧履带液压马达的驱动力矩；F_L为内外侧履带的牵引力；R为驱动轮半径；M_i为深海履带式采矿车单侧模型质量；v为履带速度，即驱动轮线速度；R_b和R_c分别为履带受到的推土阻力和压实阻力；F_w为水阻力。

3  作业环境下的阻力计算

3.1  压实阻力

履带式采矿车行驶在海底稀软沉积物上，沉陷较大，不可避免地将产生较大的压实阻力与推土阻力。压实阻力可由下列公式得到^[9]：

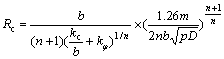      (7)

其中：k_c和k_φ分别为内聚变形模量和摩擦变形模量； m为车体质量；n为单条履带支重轮数；b为履带宽度；p为履带板节距；D为支重轮直径。

3.2  推土阻力

推土阻力可由参考文献[10]得到：

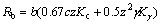        (8)

其中：γ为沉积物湿密度；z为沉陷量；K_c和K_γ为被动土系数，其中，

          (9)

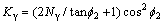        (10)

这里，N_c和N_γ为太沙基承载能力系数^[11]，由土壤内摩擦角φ₂唯一确定，可通过太沙基承载力系数表获得。

3.3  水阻力

水下履带式采矿车有较大的迎水体积及迎水面积，海水密度较大，且海底存在着一定的洋流，这些都对采矿车有一定的动力影响。水动力可以由水阻力和惯性力线性叠加而成^[12]：

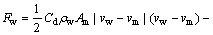
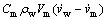           (11)

其中：C_d为水阻力系数(drag co-efficiency)；C_m为附加质量系数；ρ_w为海水密度；A_m为采矿车的迎水面积；v_m和v_w分别为采矿车的行驶速度与海流速度。根据我国深海采矿系统对采矿车行走速度的要求，本文以0.5 m/s作为采矿车行走控制速度；海底洋流速度根据我国大洋多金属结核中试系统1 000 m海试区域的介绍，约为0.15 m/s。

3.4  转弯阻力

对于履带式采矿车而言，其转向是通过左右履带差速来实现的，在转弯的过程中由于偏心的存在导致转弯阻力的产生，转弯阻力可通过下式计算得到^[13]

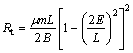       (12)

式中：m为履带车质量，B为履带间距，L为车体长度，E为纵向偏心距，阻力系数μ取0.23。阻力计算参数见表3。

由表1~3和计算式(7)~(12)可以得到深海履带式采矿车行驶过程受到的行驶阻力约为31 510 N，对应牵引力与打滑率关系曲线可知，此时的打滑率为29%。由于采矿车在行驶的过程中还会受到与之相连的输送软管的作用力，所以履带的打滑率应该有一定的余量。故本文取20%作为履带式采矿车打滑率的控制标准。

表3  阻力计算参数

Table 3  Parameters of resistance

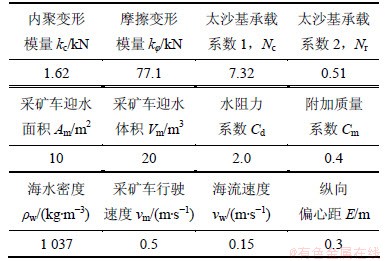
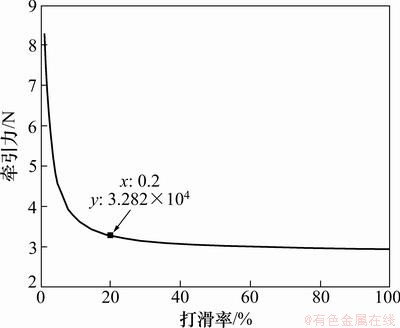
图2  期望打滑率示意图

Fig. 2  Expected slip rate

4  采矿车液压行走系统模型

深海履带式采矿车左右履带的行走均采用液压系统来实现。该液压系统是一个液压阀控马达系统，由变量泵、电液比例阀、定位油缸、液压马达等组成，如图3所示。它通过改变电液比例阀控制油缸位移，进而改变液压泵斜盘倾角，调节液压回路流量来控制液压马达的转速和方向，从而达到深海履带式采矿车前进、后退及转弯的目的。

液压马达为深海履带式采矿车提供动力，液压行走系统模型的输入量为比例阀的控制电流，输出量为液压马达的输出转矩，通过控制比例阀的输入电流就对液压马达输出转矩的调整，进而控制驱动轮的驱动力矩，从而达到调节履带的打滑率的目的。

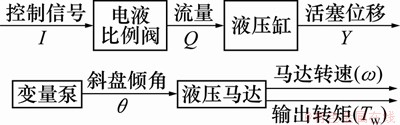
图3  采矿车液压行走系统框图

Fig. 3  Diagram of walking hydraulic system of miner

5  控制系统设计

5.1  控制系统结构

为使采矿车在直线行驶过程打滑率满足控制要求，设计带模糊PID控制器的打滑率控制系统，控制系统如图4所示。

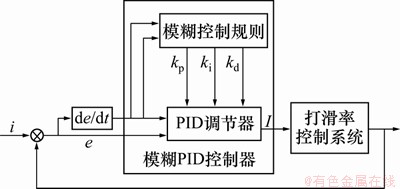
图4  模糊PID控制系统框图

Fig. 4  Fuzzy PID control system

在模糊PID控制器中，控制变量为打滑率i，调节变量为履带液压行走系统比例阀的输入电流I，打滑率偏差e以及偏差变化率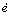可以实时计算，根据模糊关系可调整此PID控制器的参数k_p，k_i和k_d。

5.2  模糊PID控制器设计

模糊控制的输入为控制变量i的偏差以及偏差变化率，输出为PID调节器的参数k_p，k_i，k_d；E和E_C为e和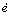的模糊变量，K_P，K_I和K_D为模糊变量。它们的论域均为{±6，5，4，3，2，1，0}，模糊集均为{P_B，P_M，P_S，Z，N_S，N_M，N_B}。图5所示为各个模糊变量的隶属度函数曲线。

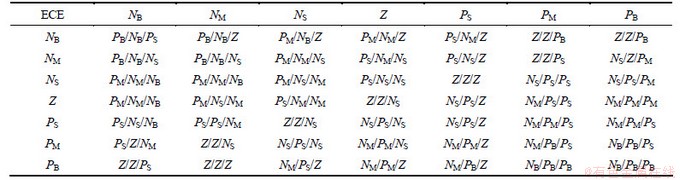
在模糊PID调节器中，K_P，K_I和K_D模糊参数由控制规则得出。表4给出了模糊规则模型，由表4可知，在|E|比较大的情况下，采用PD控制，可以达到加快相应速度并快速消除稳态误差的作用；在|E|适中的情况下，以保证控制精度为目标；而在|E|较小的情况下，K_P和K_D取大值，用以提高系统的稳定性。

采用重心法进行反模糊化，最终得到PID调节器的参数k_p，k_i，k_d。

图5  各模糊变量隶属度函数

Fig. 5  Degree of membership of fuzzy variables

5.3  打滑反向计算模型

由于采矿车行驶在极其稀软的海底，其行走过程必然存在一定的打滑。采矿车打滑率的计算可通过下式得到：

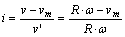          (13)

根据我国深海采矿系统对采矿车行走速度的要求，v_m=0.5 m/s。

根据上述模糊PID控制系统，在Matlab/Simulink中建立仿真模型，如图6所示。此系统的输入为期望打滑率(20%)，输出为深海履带式采矿车驱动轮的线速度。液压行走模块根据图3建立，限于文章篇幅，液压行走模型的Simulink建模过程参考文献[14-15]。打滑反向计算模块根据式(13)建立。

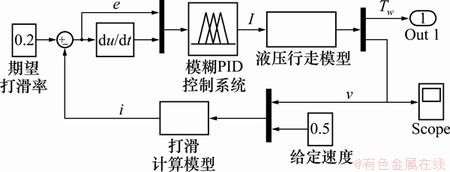
图6  仿真框图

Fig. 6  Simulink model

表4  K_P，K_I，K_D模糊规则

Table 4  Fuzzy rule of K_P, K_I, K_D

6  仿真分析

图7和8分别为打滑率控制仿真曲线和履带式采矿车驱动轮速度仿真曲线。

由图7可以看出：在模糊PID控制器的作用下，深海履带式采矿车直线行驶启动阶段打滑率较高，最高达到54%，之后在控制器的作用下迅速逼近理想打滑率(20%)，大约在0.65 s达到稳定(20%)，此后一直稳定在理想打滑率附近，符合控制要求。

由图8可以看出：采矿车启动阶段驱动轮速度由0 m/s迅速增大，约在0.65 s时达到稳定，速度稳定在0.625 m/s左右，对应采矿车设定的行驶速度0.5 m/s可知，打滑率基本稳定在20%左右。图8的仿真结果与图7打滑率的变化规律吻合，由此验证了履带式采矿车行走液压动力系统模型的正确性。

综上仿真结果，整个控制系统能使深海履带式采矿车迅速稳定在最佳工作状态，确保了采矿车行驶过程中的动力性能。

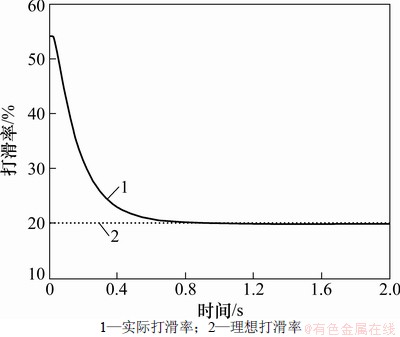
图7  打滑率仿真曲线

Fig. 7  Simulation result of slip rate

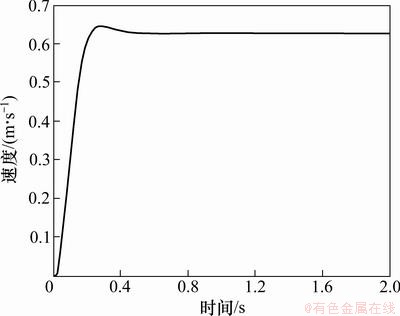
图8  驱动轮速度仿真曲线

Fig. 8  Simulation result of velocity of drive wheel

7  结论

(1) 基于我国深海采矿特定海泥层土力学特性分析，得到深海履带式采矿车牵引力与打滑率之间的关系：牵引力随打滑率增加而急剧减小，最终稳定在30 kN。为我国深海采矿车动力学分析提供理论基础。

(2) 建立完整的履带式采矿车动力学模型，根据采矿车牵引力与打滑率之间的关系，通过对各阻力分析和理论计算，提出采矿车直线行走打滑率不高于20%的控制要求。

(3) 基于深海履带式采矿车行走液压动力系统模型，在Simulink环境下设计了带模糊PID控制的履带式采矿车控制系统，并进行直线行走仿真。仿真结果表明，采矿车打滑率能快速逼近有效的控制在要求范围内，稳态性好，保证了采矿车良好的行走动力性能。

(4) 未来将进行软管阻力对深海履带采矿车行走过程动力影响的研究，以及深海采矿整体系统联动过程等方面的研究。

参考文献：

[1] Zvi S, William S, Minh H. Trajectory planning of tracked Vehicles[C]//Serate W. Proceedings of International Conference on Robotics and Automation. Los Angeles, 1993: 796-801.

[2] Bekker M G. Theory of land locomotion[M]. Michigan: Ann Arbor, University of Michigan Press, 1956: 350-380.

[3] Schulte E, Handschuh R, Schwarz W. Transferability of soil mechanical parameters to traction potential calculation of a tracked vehicle[C]//International Society of Offshore and Polar Engineers. Proceedings of the 5th ISOPE Ocean Mining Symposium. Tsukuba Japan: ISOPE, 2003: 123-131.

[4] 李力, 李庶林. 深海表层海泥模拟及地面力学特性研究[J]. 工程力学, 2010, 27(11): 213-220.

LI Li, LI Shulin. Simulation and mechanical characteristics of terramechanics of the surface soil on deep-sea bed[J]. Engineering Mechanics, 2010, 27(11): 213-220.

[5] 张成宝, 吴光强, 丁玉兰, 等. 汽车驱动防滑的控制方法研究[J]. 汽车工程, 2000, 22(5): 324-328.

ZHANG Chengbao, WU Guangqiang, DING Yulan, et al. A research on the control method of vehicle anti-slip regulation[J]. Automotive Engineering, 2000, 22(5): 324-328.

[6] FNA Zhejun, Yoram Koren, David Wehe. A simple traction control for tracked vehicles[C]//Proceedings of the American Control Conference, Washington, 1995: 1176-1177.

[7] Herzog K, Schulte E, Atmanand M A, et al. Slip control system for a deep-sea mining machine[J]. Journal of Automation Science and Engineering, 2007, 4(2): 282-286.

[8] Wong Y. Theory of ground vehicle[M]. Canada: John Wiley & Sons, Inc, 2001: 90-93.

[9] Kogure K, Ohira Y, Yamaguchi H. Prediction of sinkage and motion resistance of a tracked vehicle using plate penetration test[J]. Journal of Terramechanics, 1983, 20(3): 121-128.

[10] 张克健. 车辆地面力学[M]. 北京: 国防工业出版社, 2002: 355-399.

ZHANG Kejian. Vehicle terramechanics[M]. Beijing: National Defense Industry Press, 2002: 355-399.

[11] Terzaghi K. Theoretical soil mechanics[M]. New York: Wiley, 1966: 289-365.

[12] Myers J J, Carl H, Holm R H, McAllister. Handbook of ocean and underwater engineering[M]. New York: McGraw-Hill, 1969: 125-265.

[13] 陈世教. 履带式液压挖掘机原地转弯阻力计算[J]. 建筑机械, 1998, 4: 6-9.

CHEN Shijiao. Calculation of steering resistance of crawler hydraulic excavator in place[J]. Construction Machinery, 1998, 4: 6-9.

[14] 戴瑜. 履带式集矿机海底行走的单刚体建模研究与仿真分析[D]. 长沙: 中南大学机电工程学院, 2010: 74-76.

DAI Yu. The modelling research and simulation analysis on the single-rigid-body of tracked miner moving on the seafloor[D]. Changsha: Central South University. College of Mechanical and Electrical Engineering, 2010: 74-76.

[15] 陈锋. 深海底采矿机器车运动建模与控制研究[D]. 长沙: 中南大学信息科学与工程学院, 2005: 41-63.

CHEN Feng. Study of deep seabed mining robot vehicle motion modeling and control[D]. Changsha: Central South University. School of Information Science and Engineering, 2005: 41-63.

(编辑  陈爱华)

收稿日期：2012-10-05；修回日期：2012-12-20

基金项目：国家自然科学基金资助项目(51074179)；国家高技术研究发展计划(“863”计划)项目(2012AA091201)

通信作者：韩庆珏(1980-)，男，河南新乡人，博士研究生，从事海底履带采矿车研究；电话：15973129559；E-mail：qingjuehan@yahoo.com.cn

摘要：在分析我国深海底海泥特性的基础上，利用膨润土模拟海泥，得到深海履带式采矿车牵引力和打滑率之间的关系。牵引力随打滑率增加而急剧减小，最终稳定在30 kN。通过对推土阻力、压实阻力、转弯阻力、水阻力的理论分析，建立履带式采矿车的动力学模型，提出了采矿车直线行走时打滑率i应≤20%的控制要求，并设计带模糊PID控制器的打滑率控制系统。利用Simulink软件，对控制系统进行仿真。仿真结果表明，所设计的打滑控制系统能够满足深海履带式采矿车行走控制要求，打滑率控制响应速度快、稳态性好，保证采矿车良好的动力性能。