J. Cent. South Univ. Technol. (2008) 15(s1): 001-004
DOI: 10.1007/s11771-008-301-7
Research advances of un-symmetric constitutive theory of anisotropic viscoelastic liquids and its hydrodynamic behavior
HAN Shi-fang(韩式方)
(Chengdu Institute of Computer Application, Chinese Academy of Sciences, Chengdu 610041, China)
Abstract:
Research advances of un-symmetric constitutive equation of anisotropic fluid, influence of un-symmetric stress tensor on material functions, vibrational shear flow of the fluid with small amplitudes and rheology of anisotropic suspension were reported. A new concept of simple anisotropic fluid was introduced. On the basis of anisotropic principle, the simple fluid stress behaviour was described by velocity gradient tensor F and spin tensor W instead of velocity gradient tensor D in the classic Leslie-Ericksen continuum theory. Two relaxation times analyzing rheological nature of the fluid and using tensor analysis a general form of the constitutive equation of co-rotational type was introduced. More general model LCP-H for the fluid was developed. The unsymmetry of the shear stress was predicted by the present continuum theory for anisotropic viscoelastic fluid-LC polymer liquids. The influence of the relaxation times on material functions was specially studied. It is important to study the unsteady vibrational rotating flow with small amplitudes, as it is a best way to obtain knowledge of elasticity of the LC polymer, i.e. dynamic viscoelasticity. For the shear-unsymmetric stresses, two shear stresses were obtained thus two complex viscosities and two complex shear modulus (i.e. first and second one) were introduced by the constitutive equation which was defined by rotating shear rate introduced by author. For the two stability problems of fluid, such as stability of hydrodynamic flow and orientational motion, were discussed. The results show that the polymer suspension systems exhibit anisotropic character. The PNC systems can exhibit significant shear-thinning effects. For more concentrated polymer nano-suspensions, the first normal stress difference change from positive to negative, which is similar to LC polymer behavior.
Key words:
1 Introduction
The liquid crystalline (LC) polymer is considered a typical anisotropic viscoelastic fluid. The anisotropic fluid involves not only LC polymer but also suspension liquids including polymer nano-composites (PNC). In research on constitutive equation theory of LC polymers important developments of molecular theory were made by DOI (1986), which is the base of a series of the investigations now. For describing molecular orientation, a “director vector” n was introduced, which represented the direction of preferred orientation of molecules in the neighborhood of any point. For the fluid orientational motion of the director vector, hydrodynamic fluid motion was considered to develop the continuum theory of the nematic fluid. The Ericksen-Leslie continuum theory[1-3] described the main features flow of nematic liquid crystal of low molecular mass or the flow at low shear rates. The convected constitutive equation of Oldroyd type was well used for the isotropic polymer solutions or melts in Non-Newtonian fluid mechanics, but rarely for the anisotropic LC fluid case. The first attempt was given by VOLKOV and KULICHIKHIN for LC polymer fluid[4]. Using the Maxwell linear equation (1867) for anisotropic liquid crystals, a convected Maxwell model with relaxation was introduced, and viscosity tensor, a constitutive equation with un-symmetric shear viscosity was developed by the authors.
2 Constitutive equation of co-rotational type for LC polymer
Another new approach to continuum theory of the constitutive equation of Maxwell-Oldroyd type was first proposed for LC polymer liquids by HAN (the 3rd International Conference on Fluid Mechanics, 1998) by convected co-rotational time derivative, the theory was specialized by the LCP-B model[5-6]. The equation of both fluid and orientational motions were considered. The anisotropic material functions, such as anisotropic viscosity, relaxation and retardation times, were introduced to describe the anisotropic behavior of the material. The theory predicted the special behavior of the first and second normal stress differences, which agreed with experiments by BAEK, MAGDA, LARSON,HUDSON (1993, 1994). The experimental results of change curves of first and second normal stress differences with shear rate are shown in Fig.1.
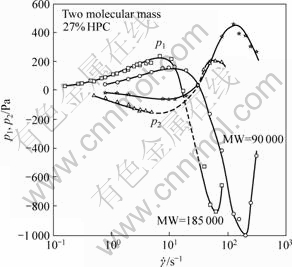
Fig.1 Change curves of first and second normal stress differences with shear rate
In order to study the macroscopic rheological behaviour of LC polymer fluid, a special investigation was given[7] when the orientational motion of the director was effected by the hydrodynamic motion, but there was no principle influence on the hydrodynamic motion by the orientational motion. The developed theory was used to successfully explain the macroscopic behavior of normal stress differences behavior[5-8].
A new concept of anisotropic simple fluid was introduced. Instead of velocity gradient tensor D in the classic Leslie-Ericksen continuum theory, the stress behaviour was described by first Rivlin-Ericksen tensor A and spin tensor W measured with respect to co-rotational coordinate system. Using the tensor analysis approach[9-10] to analyze the physical nature of the fluid, more general theory was developed for constitutive equation of the fluid. The constitutive equation was split into two parts.
1) Normal-symmetric stress action part
2) Shear un-symmetric part
where λn is relaxation time of the normal?symmetric stress components; λs is relaxation time of the normal?symmetric stress components. The theory is specialized to a new model LCP-Qs.
Fig.2 shows theoretical results of the first normal stress σ1 and second normal stress σ2 differences vs shear rate 
with variation of director vector, respectively, calculated by LCP-Qs model. The special behavior of the normal stresses is shown in Fig.2 that the first normal stress difference changes from positive value to negative value then to positive value, the second normal stress difference changes from negative value to positive value then to negative value. The apparent viscosity η vs shear rate is shown with variation of director vector. Remarkable influence of molecular orientation on the apparent viscosity, first and second normal stresses are observed, when the director vector is tumbling from flow direction to that perpendicular to it. The present phenomena can be considered the results of director tumbling[11]. The first and second normal stress difference functions p1 and p2 are shown in Fig.3.
Fig.2 Change curves of first normal stress σ1(a) and second normal stress differences σ2(b) with shear rate 
(parallel and vertical to flow direction)
3 Un-symmetry of constitutive equation
For the case, when the director is parallel to flow direction sinθ=0, cosθ=1 because of two shear stresses,
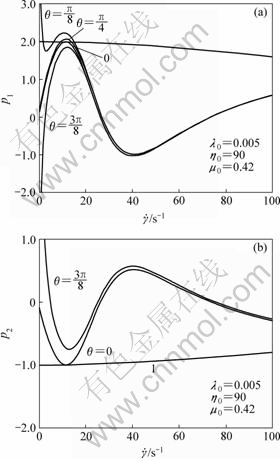
Fig.3 Change curves of first and second normal stress difference functions p1(a) and p2(b) with shear rate of LCP–Qs model
the first and second apparent viscosities are obtained and given by[9]
and
Fig.4 shows change curves of the first and second apparent viscosities with shear rate when director is parallel and vertical to the flow direction, respectively. The two shear stresses thereby in shear flow of LC polymer liquids lead to un-symmetric constitutive equation and vortex flow and rotation flow in it. The oscillation of first apparent viscosity with director angle is shown in Fig.5. From Fig.5, the present phenomenon could be a theoretical basis of the modern liquid crystalline display technology.
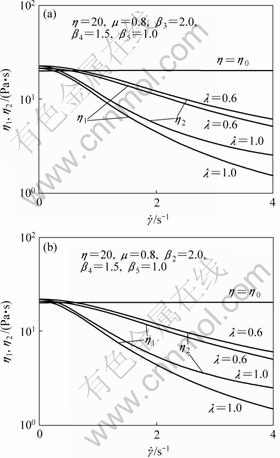
Fig.4 Change curves of first and second apparent viscosity with shear rate: (a) Parallel director; (b) Vertical director (with variation of relaxation time)
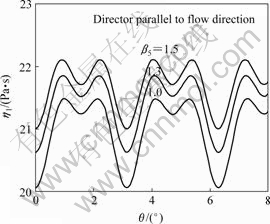
Fig.5 Curves of first apparent viscosity vs director angle (with variation of anisotropic viscosity β5)
4 Two types of stability problem
The anisotropic fluid flow of two types of the stability problem was discussed[9, 11-12].
1) Stability of hydrodynamic motion of the fluid flow
2) Stability of orientational motion of director vector
2-D disturbed theory of orientational motion, such as extensional and shear flow, was studied. Fig.6 shows disturbed amplitude function p(t) vs λkt for orientational extensional flow with 2D disturbance. Disturbed amplitude function q(t) vs 
for shear flow is shown in Fig.7.
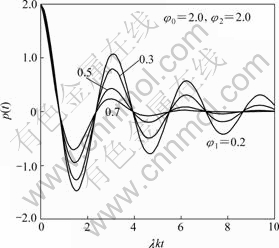
Fig.6 Curves of disturbed amplitude function p(t) vs λkt for orientational extensional flow with 2D disturbance
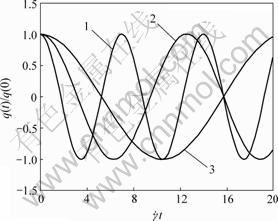
Fig.7 Curves of disturbed amplitude function q(t) vs 
for shear flow
5 Vibrational rotating flow with small amplitude
A vibrational rotating flow in gap between cylinders with small amplitudes was studied for the anisotropic viscoelastic fluid-liquid crystalline polymer[9].
For the shear-unsymmetric stress action, the first and second complex shear viscosities are obtained by the first and second un-symmetric shear stress components. Because of un-symmetry of the stress tensor, three complex shear modulus, the complex viscosity 
with action of normal-symmetric stress, the complex viscosities 
and 
with action of shear un-symmetric stresses were introduced. The anisotropic fluid stress components should be sum of normal- symmetric stress and shear un-symmetric stress components.
6 Rheology of anisotropic suspension
The polymer suspension systems exhibit anisotropic character. Polymer nano-composites are obtained by dispersing a few mass fraction of nanoscopic particulate fillers in polymer matrices. The research results show that the PNC systems can exhibit significant shear- thinning effects. For more concentrated polymer nano- suspensions, the first normal stress difference decreases to a positive value at low shear rates and a negative value at high rates, a little are similar to LC polymer behavior.
References
[1] ERICKSEN J L. Conservation laws for liquid crystals[J]. Trans Soc Rheol, 1961, 5(1): 23-34.
[2] LESLIE F M. Theory of flow phenomena in liquid crystals in advances in liquid crystals[C]// Advances in Liquid Crystals. New York: Academic, 1979: 1.
[3] CHANDRASEKHAR S. Liquid crystals[M]. Cambridge: Cambridge Univ Press, 1977.
[4] VOLKOV V S, KULICHIKHIN V G. Un-symmetric viscoelasticity of anisotropic polymer liquids[J]. Rheol Acta, 2000, 39(3): 360-370.
[5] HAN Shi-fang. Constitutive equation and computational analytical theory of non-Newtonian fluids[M]. Beijing: Science Press, 2000. (in Chinese)
[6] HAN Shi-fang. Constitutive equation of liquid crystalline polymer-anisotropic viscoelastic fluid[J]. Acta Mechanica Sinica, 2001, 33(5): 588-600. (in Chinese)
[7] HAN Shi-fang. Constitutive equation of co-rotational derivative type for anisotropic viscoelastic fluid[J]. Acta Mechanica Sinica, 2004, 20(1): 46-53.
[8] HAN Shi-fang. A constitutive equation of co-rotational type for liquid crystalline polymer and anisotropic material functions, keynote lecture, advances in rheology and its applications[C]// Proc of 4th Pacific Rim Conference on Rheology. USA: Science Press, 2005: 22-27.
[9] HAN Shi-fang. Continuum mechanics of anisotropic non-Newtonian fluids—Rheology of liquid, crystalline polymer[M]. Beijing: Science Press, 2008. (in Chinese)
[10] HAN Shi-fang. An unsymmetric constitutive equation for anisotropic viscoelastic fluid[J]. Acta Mechanica Sinica, 2007, 23(2): 149-158.
[11] HAN Shi-fang. Stability of shear-extensional flow in film extrusion of liquid crystalline polymer-anisotropic viscoelastic fluid[C]// Proc of XVth International Congress on Rheology. California, 2008.
[12] LARSON R G. Roll-cell instability in shearing flows of nematic polymers[J]. J of Rheology, 1993, 39(2): 175-197.
Foundation item: Project(10772177) supported by the National Natural Science Foundation of China
Received date: 2008-06-25; Accepted date: 2008-08-05
Corresponding author: HAN Shi-fang, Professor; Tel: +86-28-66142335; E-mail: sfh5578@sina.com
