
J. Cent. South Univ. (2018) 25: 2002-2013
DOI: https://doi.org/10.1007/s11771-018-3890-9
A self-regulating pairwise swapping algorithm to search reliability-based user equilibrium
ZHANG Wen-yi(张文义), GUAN Wei(关伟), FAN Ling-ling(樊玲玲)
MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology,Beijing Jiaotong University, Beijing 100044, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract:
The violation of monotonicity on reliability measures (RMs) usually makes the mathematical programming algorithms less efficient in solving the reliability-based user equilibrium (RUE) problem. The swapping algorithms provide a simple and convenient alternative to search traffic equilibrium since they are derivative-free and require weaker monotonicity. However, the existing swapping algorithms are usually based on linear swapping processes which cannot naturally avoid overswapping, and the step-size parameter update methods do not take the swapping feature into account. In this paper, we suggest a self-regulating pairwise swapping algorithm (SRPSA) to search RUE. SRPSA comprises an RM-based pairwise swapping process (RMPSP), a parameter self-diminishing operator and a termination criterion. SRPSA does not need to check the feasibility of either solutions or step-size parameter. It is suggested from the numerical analyses that SRPSA is effective and can swap to the quasi-RUE very fast. Therefore, SRPSA offers a good approach to generate initial points for those superior local search algorithms.
Key words:
travel time reliability; reliability-based user equilibrium; day-to-day dynamics; route swapping;
Cite this article as:
ZHANG Wen-yi, GUAN Wei, FAN Ling-ling. A self-regulating pairwise swapping algorithm to search reliability-based user equilibrium [J]. Journal of Central South University, 2018, 25(8): 2002–2013.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-018-3890-91 Introduction
A central subject in transportation planning and evaluation, as well as system analysis in the context of deterministic and stochastic traffic networks is to find the traffic equilibrium states. This subject has stimulated an ever-growing and significant research topic in transportation research, i.e., developing effective algorithms to solve the traffic equilibrium problems under various route choice behaviors. During the past several decades, various traffic equilibrium models were proposed. In this paper, we focus on the reliability-based user equilibrium (RUE) problem.
The method to study the stochastic RUE problem of urban traffic networks is the reliability-based modeling methodology. Within the framework of this methodology, when a traveler makes a route choice decision, she/he aims not only to minimize the path travel time but also to improve the travel punctuality (or say reliability). To capture this travel behavior, many travel time reliability measures (RMs) were developed, such as the percentile travel time [1], travel time budget [2], mean-excess travel time [3], combined mean travel time [4]. If travelers pursue the paths with the least RM during the routing decision, these collective self-routing actions will finally result in a long-term habitual and steady traffic state, namely, RUE, and traffic only distributes on the paths with the minimum RM.
Besides modeling RUE, another important task is to solve RUE; to date, the path-based algorithms serve as the main choice to deal with this task. However, these algorithms [5–9] usually require that the path cost measures are continuously differentiable and strictly (or strongly) monotone with respect to the path flow vector. For above RMs, the requirement on monotonicity is usually hard to enforce, which thus makes the algorithms less efficient. Another branch of the path-based algorithms is based on path-swapping. These algorithms solve the traffic equilibriums by swapping traffic between paths based on the cost differences. The swapping algorithm has a direct and plausible behavioral interpretation, i.e., traffic will swap from the more costly paths to the less costly ones; in addition, they are derivative-free and require much weaker monotonicity on the path cost measures [10]. Since the inner running mechanism of the swapping algorithms is different from that of the line-search-based mathematical programming algorithms, it is too difficult to analytically discuss their convergence. Thus, they are usually called as swapping heuristics.
Literatures on swapping algorithms can be categorized as three classes according to different swapping rules, i.e., 1) swapping from more costly paths to the least costly ones [11, 12], 2) swapping from the most costly paths to the least costly ones [13, 14], and 3) pairwise swapping [15]. For brevity, we simplify swapping rules 1) and 2) as more-to- least and most-to-least swapping, respectively. MOUNCE et al [16] analyzed several continuous- time swapping dynamics and found that only the pairwise swapping dynamics was Lipschitz continuous. Recently, MOUNCE et al [15] gave a sufficient condition to find the convergent sequences of the step-size parameters for the proportional-switch adjustment process (PAP) [17]. Note that the step-size updating approach of the classical method of successive averages (MSA) [18] meets this condition. Except the above three kinds of swapping algorithms, CAREY et al [19] suggested a nonlinear swapping algorithm that comprised a paired swapping manner (i.e., most-to- least, second-most-to-second-least) and a MSA-like step-size updating method; this swapping algorithm was recently employed by RASMUSSEN et al [20] to solve the restricted stochastic user equilibrium problem.
For above-reviewed swapping algorithms, apart from Refs. [13, 14], the rest ones are explicitly based on a swapping model and adjust the swapping amount by regulating the step-size parameter. This study still follows this line. As a numerically swapping algorithm, the manual manner (e.g., Ref. [11]) is not applicable to find the step-size parameters. The sufficient condition given by MOUNCE et al [15] is applied to finding the step-size parameter sequence for the linear PAP, which, however, is not valid for the nonlinear swapping processes (e.g., those in Refs. [19, 21]). The MSA-like method [19] updates the step-size only according to the number of iterations, which does not take the swapping process into account. In this work, we first develop a RM-based pairwise swapping process (RMPSP), and then a self- decreasing operator (SDO) is proposed to update the step-size parameter, deriving the present self- regulating pairwise swapping algorithm (SRPSA). SRPSA can naturally keep the solutions feasible. It is shown from the numerical simulation that the present SDO is effective and SRPSA can quickly approach to the RUE.
The remainder of this paper is organized as follows. In Section 2, several typical RMs and a general RUE model are introduced. In Section 3, RMPSP is developed and comprehensively analyzed. In Section 4, SDO and SRPSA are given. In Section 5, a numerical comparison is conducted to examine the performance of SRPSA. In Section 6, the conclusions of this paper are given and some further works are suggested.
2 Background: RUE model
Within the framework of RUE theory, RM is defined as the path performance measure to capture the traveler’s concern for the reliability. Regardless of the travel time distribution, FOSGERAU et al [22] verified that the maximal expected utility of a path can always be formulated as the linear combination of the mean and standard deviation of travel time on this path, which leads to a general form of RM, i.e.,
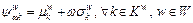 (1)
(1)
where W is the set of OD-pairs; Kw is the set of acyclic paths between OD-pair w; α is the travel reliability;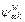 is the RM indicator on path k between OD-pair w;
is the RM indicator on path k between OD-pair w; 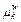 is the mean travel time of path k between w;
is the mean travel time of path k between w;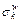 is the standard deviation of travel time on path k between w; ω is an reliability-related parameter that reflects traveler’s risk attitude to uncertainty.
is the standard deviation of travel time on path k between w; ω is an reliability-related parameter that reflects traveler’s risk attitude to uncertainty.
A positive ω implies the risk-averse routing behavior, a negative ω implies the risk-prone routing behavior, and a zero ω implies risk-neutral routing behavior. When the path travel times follow the normal distribution and let Φ–1(·) be the inverse of the standard normal distribution, the formulations of ω for four typical RMs are stated in Table 1.
According to Table 1, the mean-below travel time measure is a purely risk-prone RM, while the mean-excess travel time measure is a purely risk-averse RM. The travel time budget measure can capture various risk attitudes when α takes different values. Since the weight factor υ takes values from 0 to 1, the combined mean travel time measure can capture various risk attitudes as well.
Considering a fully-connected network and given that the travel demand is fixed, the feasible path flow set Ω1 can be expressed as follows:
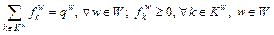 (2)
(2)
where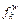 is the flow on path k between OD-pair w; qw is the travel demand between w.
is the flow on path k between OD-pair w; qw is the travel demand between w.
In Eq. (2), the first equation is the conservation constraint associated with travel demands, and the second inequality is the non-negative constraint associated with path flows.
In a stochastic traffic network, when all travelers try to select the paths with the minimum RM in their trips, this kind of behavior dictates that people adjust paths until they cannot find a better path, and then a long-term habitual steady-state or traffic equilibrium will be reached. Such a steady-state can be described as in Definition 1.
Definition 1 (RUE). At RUE, all used paths connecting the same OD-pair have the minimal and equal alpha-reliable RM. Mathematically, the following equalities and inequalities hold in general.
 (3)
(3)
In Eq. (3), πw is the minimal RM between w, and superscript ‘ ’ indicates the equilibrium. Definition 1 implies that traffic only locates on the paths with the minimal RM, and nobody has the incentive to change path unilaterally at RUE. Below, we give the equivalent variational inequality expression of RUE.
’ indicates the equilibrium. Definition 1 implies that traffic only locates on the paths with the minimal RM, and nobody has the incentive to change path unilaterally at RUE. Below, we give the equivalent variational inequality expression of RUE.
Proposition 1: RUE is equivalent to the following variational inequality problem:
 (4)
(4)
where vectors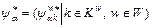 and
and 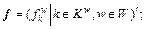 Superscript ‘′’ is the transposition operator.
Superscript ‘′’ is the transposition operator.
Proof: The proof can be obtained by substituting RM for the path travel time in the proof between Wardrop equilibrium and its variational inequality model in Ref. [23]. For the brevity of presentation, we do not state it here again.
Proposition 2: Given that RM is positive and continuous, the RUE model has at least one solution.
Proof: Since set Ω1 defined by Eq. (2) is nonempty and convex, and ψα(·) is continuous, the above variational inequality problem has at least one solution [24].
3 RMPSP
This section elaborates on the RMPSP. The formulation of RMPSP is stated and a critical property is then examined; finally, a simple numerical example is performed to discuss the stability of RMPSP. From this section on, if necessary, time superscripts will be added to the relevant notations emerged in Section 2 to distinguish the states at different phases.
Table 1 Formulations of ω for four typical RMs

3.1 RMPSP
RMPSP is revised from the nonlinear pairwise swapping dynamics (NPSD) [21] which is developed to describe travelers’ day-to-day route swapping behavior. NPSD can be viewed as the nonlinear version of the classical PAP [17]. Compared with PAP, NPSD can avoid the over-swapping problem and capture travelers' nonlinear route swapping behavior better. RMPSP is mathematically formulated as follows.
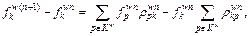
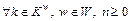 (5)
(5)
where
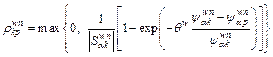 (6)
(6)
where
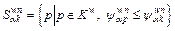 (7)
(7)
n is the time index;  is the flow on path k between w at time n; θw is a positive constant that reflects the cost sensitivity between w;
is the flow on path k between w at time n; θw is a positive constant that reflects the cost sensitivity between w;  is the set of paths whose RM is less than path k;
is the set of paths whose RM is less than path k; 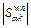 is the number of paths contained in
is the number of paths contained in  (since k belongs to
(since k belongs to 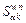 ,
, 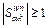 holds in general);
holds in general);  calculates the proportion of flow swapping from path k to path p between w at time n.
calculates the proportion of flow swapping from path k to path p between w at time n.
Compared with NPSD, three revisions are made for RMPSP: 1) RM replaces the original travel time; 2) the relative RM difference replaces the original absolute travel time difference; 3) the symbol ‘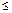 ’ replaces the original ‘
’ replaces the original ‘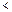 ’ in Eq. (7). The first revision is a natural tailoring to the RUE problem; the second one is to remove the effect of dimension; the third one is to keep
’ in Eq. (7). The first revision is a natural tailoring to the RUE problem; the second one is to remove the effect of dimension; the third one is to keep 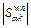 non-zero consistently, which may decrease computational time consumed in the “if–then” judgment operations.
non-zero consistently, which may decrease computational time consumed in the “if–then” judgment operations.
Below, we present several critical properties of RMPSP.
Proposition 3 (Solution invariance): For RMPSP, as soon as the initial path flow pattern is feasible, the remaining path flow patterns are still feasible. Mathematically, it means that
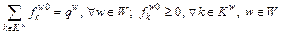 (8)
(8)
implies
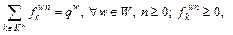
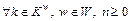 (9)
(9)
Proof: We divide the proof into two parts, i.e., path flow non-negativity and demand conservation.
Non-negativity: Since 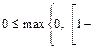
 we have
we have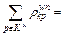

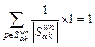 . Then it follows Eq. (5) that
. Then it follows Eq. (5) that 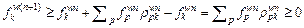 if
if 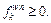 By recurrence, it gives
By recurrence, it gives 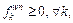
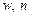 if
if 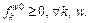
Conservation: Since 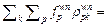
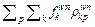 =
=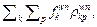 we have
we have 
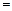
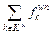 +
+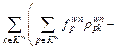
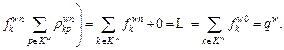
In summary, Proposition 3 holds.
Definition 2 (Stationary path flow pattern): Let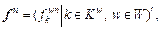 and f n be a stationary path flow pattern of RMPSP if and only if f n+1=fn.
and f n be a stationary path flow pattern of RMPSP if and only if f n+1=fn.
Proposition 4: RMPSP’s stationary path flow pattern is equivalent to RUE.
Proof: According to Definition 2, we only need to prove that f n with 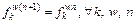 is equivalent to RUE.
is equivalent to RUE.
Sufficiency: Given that path k has the minimal RM between w (i.e.,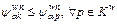 and
and  it means
it means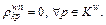 According to Eq. (5),
According to Eq. (5),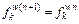 implies
implies 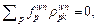 which further deduces
which further deduces  since
since  and
and  are both non-negative. Note that
are both non-negative. Note that  implies
implies 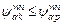 for all
for all 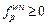 and
and 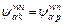 if
if 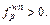 Denote
Denote  it gives
it gives 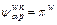 if
if 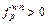 and
and 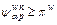 if
if 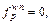 which is exactly the definition of RUE.
which is exactly the definition of RUE.
Necessity: Given that f n is at RUE, i.e., 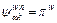 if
if 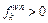 and
and 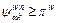 if
if  we can conclude
we can conclude 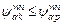 if
if 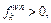 and
and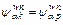 if
if 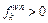 and
and  From Eq. (6), we have
From Eq. (6), we have 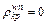 if
if 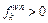 and
and 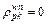 if
if 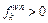 and
and  Then we can derive
Then we can derive 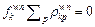 and
and 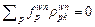 if
if 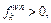 leading to
leading to 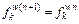 if
if 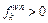 from Eq. (5). When
from Eq. (5). When  we have
we have 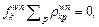 and
and 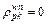 if
if 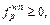 then
then 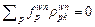 can be also derived. Recalling Eq. (5) again, we can conclude
can be also derived. Recalling Eq. (5) again, we can conclude 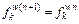 if
if  i.e., f t implies ft+1=ft.
i.e., f t implies ft+1=ft.
Propositions 3 and 4 show that, no matter which value θ takes, RMPSP can keep swapping solutions consistently feasible and guarantee that the stationary point is RUE. These two conclusions are important to develop a swapping algorithm. It means that the procedure of feasibility checking for either solution or step-size parameter is not necessary any more, which helps to simplify the algorithm and devote all the energies to improve the computational efficiency. This is the main reason why we select NPSP as the revision object of RMPSP. Another critical property for a dynamic system is the stability. Considering that an analytical method does not exist, the numerical simulation will be performed to examine the stability of RMPSP in the next subsection.
3.2 Stability analysis
The testing network (see Figure 1) consists of 4 nodes, 4 links, 1 OD-pair and 2 paths. The OD-pair (1, 4) is connected by Path 1 (link sequence: 1→3) and Path 2 (link sequence: 2→4). In Figure 1, the bracketed three numbers in each link are the label, free-flow time (min) and designed capacity (pcu/min), respectively. For brevity, units will be omitted in remaining text of this section.
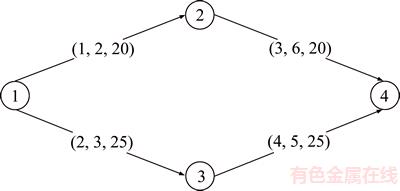
Figure 1 A simple network
In this numerical example, as well as the others, the link travel time is computed by the famous BPR function. Let 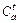 denote the travel time of link a, and it gives
denote the travel time of link a, and it gives
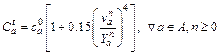 (10)
(10)
where a is the link index; A is the set of links; 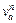 is the flow on link a at time n;
is the flow on link a at time n; 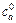 and
and 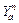 are the free-flow travel time and capacity of link a, respectively.
are the free-flow travel time and capacity of link a, respectively.
The disturbances of a stochastic traffic network can be capacity degradation, travel demand fluctuation, or both. For simplicity and without loss of generality, here we only consider the capacity degradation. Let 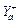 be the designed capacity of link a and assume the link capacity is distributed uniformly, i.e.,
be the designed capacity of link a and assume the link capacity is distributed uniformly, i.e., where
where 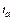 is the degradable degree of capacity, then we have
is the degradable degree of capacity, then we have
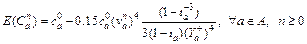 (11)
(11)
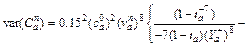
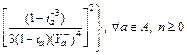 (12)
(12)
where E(·) and var(·) are the expectation and the variance operator of a random variable, respectively.
Let 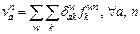 and
and 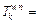
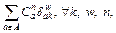 where
where 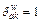 if path k uses link a and
if path k uses link a and 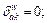 otherwise,
otherwise, 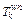 is the travel time of path k. Given that the link travel times are independent, the expectation and standard deviation of a path travel time can be expressed as follows.
is the travel time of path k. Given that the link travel times are independent, the expectation and standard deviation of a path travel time can be expressed as follows.
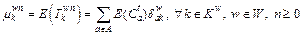 (13)
(13)
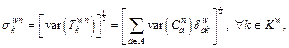
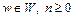 (14)
(14)
Based on Eqs. (11)–(14), we can calculate RM for all paths when the path travel time distributes normally and the link travel time is computed by BPR function.
To examine the stability of RMPSP, we perform the sensitivity analyses under θ= [0.25:0.25:5] (note that [x: y: z] groups numbers increase from x to z by step-size y). Let RM be Eq. (1) with ω=0.5. Set 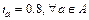 , q=45, and f 0=(22.5, 22.5). Since f 0 is not a stationary path flow pattern, it can be treated as one-day interference. The stop criterion is
, q=45, and f 0=(22.5, 22.5). Since f 0 is not a stationary path flow pattern, it can be treated as one-day interference. The stop criterion is 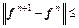

Our detailed numerical results show that: 1) when θ=[0.25:0.25:2.25], RMPSP is convergent; 2) when θ=[2.50:0.25:5.00], RMPSP finally falls into 2-day-cycled oscillations. Below, we introduce an index FD to measure the oscillation degree of the final states.
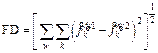 (15)
(15)
where 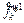 and
and  are the components of 2-day-cycled periodical traffic flows. Obviously, FD>0 if swapping is convergent and FD=0, otherwise. In addition, FD increases when the oscillation intensifies. Subsequently, we present the FDs under different sensitivities in Figure 2.
are the components of 2-day-cycled periodical traffic flows. Obviously, FD>0 if swapping is convergent and FD=0, otherwise. In addition, FD increases when the oscillation intensifies. Subsequently, we present the FDs under different sensitivities in Figure 2.
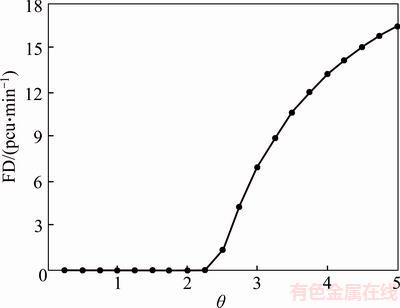
Figure 2 FDs with θ=[0.25:0.25:5.0]
Figure 2 shows FD=0 when θ=[0.25:0.25:2.25] and then becomes larger than 0 and increases as θ increases within θ=[2.50:0.25:5.00], which demonstrates that RMPSP is conditionally stable as the other discrete-time swapping dynamics. Moreover, θ plays the critical effect on the stability of RMPSP, and decreasing θ is expected to draw the oscillated swapping back to convergence. Following this conjecture, a self-decreasing mechanism for θ of RMPSP is designed in the subsequent section.
4 SRPSA
Based on the numerical result in Section 3.2, this section elaborates on a self-regulated mechanism (i.e., SDO) for RMPSP and the resulted SRPSA. It is necessary to note that, to focus on the essence, SRPSA does not include a sophisticated procedure to generate the path set although this work is also important, especially for a large-scale traffic network.
4.1 Procedure of SRPSA
For each OD pair, the present SDO to update the reaction sensitivity for RMPSP is stated as follows.
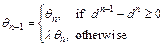 (16)
(16)
where 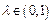 is the diminishing scalar factor and
is the diminishing scalar factor and
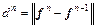 (17)
(17)
According to Eq. (16), if the deviation between two adjacent iterations enlarges, θ will be reduced until a proper one is generated. dn here is formulated as Eq. (17) since it is found from Figure 3 that dn increases as θ grows when route-swaps cannot converge. In addition, n≥2 is set to make SDO work. Since θn>0 during each swapping iteration, propositions 3 and 4 continue to hold. Obviously, λ and θ0 are two key parameters of SDO. When λ=1, SDO will not work, and SRPSA returns back to RMPSP. To keep from the impact of reduction of θ on 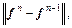 a new stop criterion is introduced, i.e.,
a new stop criterion is introduced, i.e.,
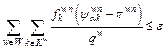 (18)
(18)
where πwn is the minimal RM between w at iteration n.
It can be concluded from Eq. (18) that ε=0 if and only if RUE is reached. Take Eqs. (16)–(18) and RMPSP together, the algorithmic procedure of present SRPSA is stated in Figure 3.
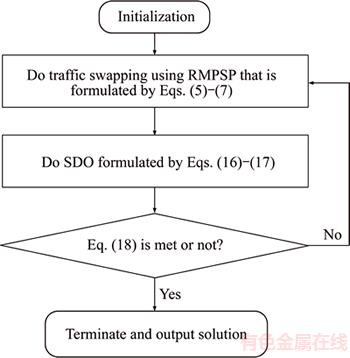
Figure 3 Flow chat of SRPSA
4.2 Numerical analysis
This numerical analysis shares the same network and almost the same input parameters with the numerical stability analysis conducted in Section 3.2. The differences including the stop criterion used here are Eq. (18) with ε=1.0×10–4, and θ here is replaced by θ0. Figure 4 performs the convergence results of RMPSP and SRPSA with different θ0 and λ.
It is shown in Figure 4 that, when θ0=[2.5:0.25:5.00], RMPSP cannot converge but SRPSAs can, which demonstrates that SDO is necessary and effective to draw non-convergent RMPSP back to convergence. In addition, it is also seen from Figure 4 that, when θ0=[4.25:0.25:5.00], the iteration times of SRPSAs with different λs differ from each other significantly, which suggests that the effect of λ is perhaps more notable than that of θ0.
5 Numerical example
This section conducts another numerical example to analyze the performance of SRPSA. Although numerical comparison between SRPSA and the modified extra-gradient method (MEGM, see Appendix A for a brief introduction) is included here, it is not (in fact it is also not enough) to rank but only to service for analysing SRPSA. To focus on the essence of the swapping algorithm, here we only employ a simple example network rather than a large-scale or realistic network to perform SRPSA and MEGM since a simple example network does not need to incorporate a sophisticated path generation procedure (the similar idea can be also found in Ref. [19]). For simplicity, the effective paths in the current numerical example consist of the acyclic paths and do not vary over the algorithmic iteration.
5.1 Testing network
The present numerical network (see Figure 5) is also used in Ref. [4], which comprises a single OD pair, 10 nodes and 13 links. Origin 1 and destination 10 are connected with six paths. In Figure 5, the bracketed three numbers in each link are the label, free-flow time (min) and designed capacity (pcu/h), respectively. For brevity, units will be omitted in remaining text of this section.
Considering that the combined mean travel time measure (recall Table 1) can capture various risk attitudes, it is applied as RM here to conduct the numerical simulation. The numerical parameters are set: the public parameters α=0.95, υ=[0:0.1:1] and q=[500:500:4000]; let (θ0, λ)=(4.0, 0.9) in SRPSA; without loss of generality, two parameter schemes are designed for MEGM, i.e., 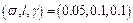 and (0.1,0.2,0.2); the stop criterion is set as Eq. (18) with ε=1.0×10–4. Note that the link travel time is still computed by Eq. (10), and Eqs. (11)–(14) are applied with
and (0.1,0.2,0.2); the stop criterion is set as Eq. (18) with ε=1.0×10–4. Note that the link travel time is still computed by Eq. (10), and Eqs. (11)–(14) are applied with 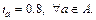
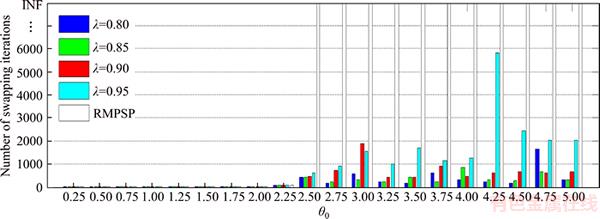
Figure 4 Convergent iteration times of RMPSP and SRPSAs (‘INF’ in the vertical axis represents an infinite number)
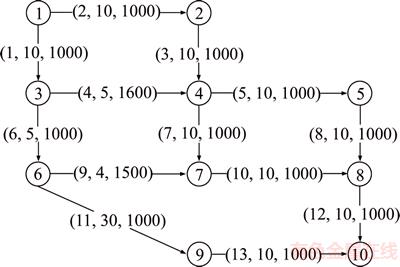
Figure 5 Testing network
5.2 Numerical results
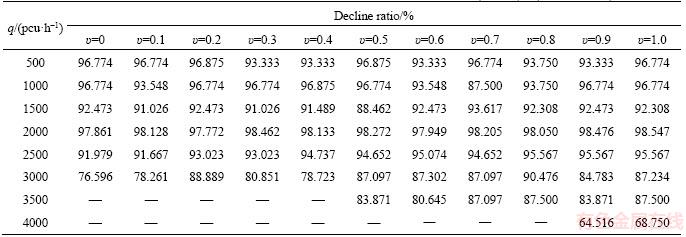
Table 2 presents the convergence results of SRPSA and two MEGMs. Table 3 states the computational time of SRPSA under different parameters. Tables 4 and 5 display the decline ratios of computational time for SRPSA in comparison with two 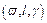 -based MEGMs.
-based MEGMs.
Table 2 indicates that two algorithms show similar convergence, and the convergent grids distribute at the upper right and the non-convergent ones distribute at the lower left. These suggest that an algorithm will perform worse when risk attitude becomes increasingly averse and travel demand rises.
It is observed from Table 3 that SRPSA consumes very little time in the convergent regions, and the convergent durations of SRPSA are not closely related to the risk-attitudes. Tables 4 and 5 indicate that SRPSA consumes much less time than MEGM in the convergent grids. Actually, in the non-convergent grids, our detailed results (do not listed here due to limited space) indicate that, SRPSA also swaps to the quasi-RUE states (with deviation less than 0.001) much faster than MEGM. However, it is still observed from our more detailed results that both SRPSA and MEGM converge very slowly when the termination tolerance ε is set to be less than ε≤1.0×10–6.
According to above numerical comparisons and analyses, SRPSA may be not an efficient local solution algorithm to directly solve RUE since it, after all, proceeds by direct RM comparison and does not use any gradient information; however, it is reasonable to infer that SRPSA can serve as a good choice to generate initial points for the other superior local optimization methods since it is simple, convenient, derivative-free, and what’s more it can swap to the quasi-RUE states very quickly.
Table 2 Convergence results of SRPSA and two MEGMs
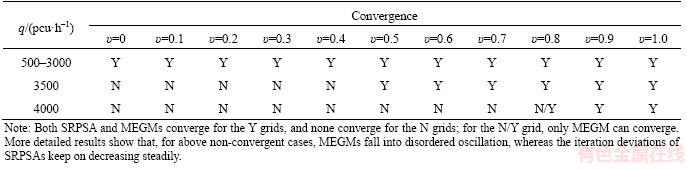
Table 3 Computational time of SRPSA
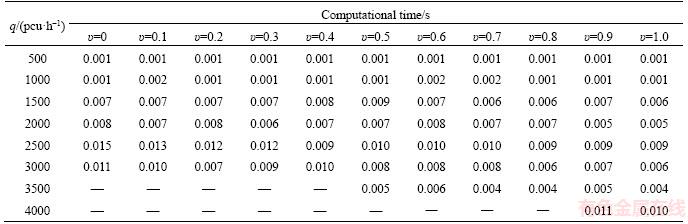
Table 4 Decline ratio in computational time for SRPSA in contrast to MEGM with 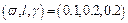
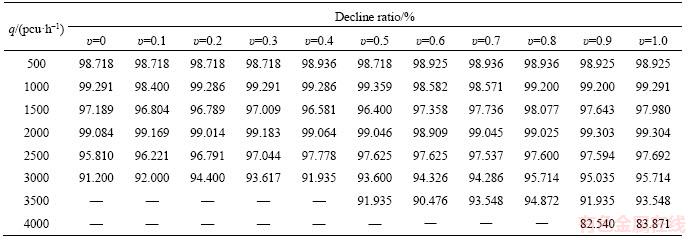
Table 5 Decline ratio in computational time for SRPSA in contrast to MEGM with 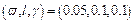
6 Conclusions and future research
This paper proposes a swapping algorithm, i.e., SRPSA, to solve the RUE problem in stochastic traffic networks. SRPSA consists of RMPSP, SDO and a termination criterion. SDO serves for finding a suitable reaction sensitivity sequence for RMPSP. Compared with the existing swapping algorithms, SRPSA does not need to check feasibility for either solution or step-size parameter, and thus is more convenient. Compared with the mathematical programming algorithms, SRPSA is simple, convenient and derivative-free; in addition, it requires much weaker monotonicity on RM, and can consistently keep solutions feasible. The numerical results suggest that: i) the designed SDO is effective since SRPSA can draw oscillated RMPSP back to convergence; ii) SRPSA converges much faster than MEGM in those convergence cases; SRPSA can swap to quasi-RUE very quickly; thus, it offers a good choice to generate initial points for the other superior local optimization algorithms.
It should be noted that, to focus on the essence, SRPSA and the numerical example stated in Section 5 do not include a well-designed method to generate effective paths on which traffic will be assigned or swapped. In addition, the results derived from the limited numerical examples need to be further examined in the large networks. Finally, a two-stage algorithm, which comprises SRPSA and a local search algorithm (e.g., those mentioned in Refs. [8, 9, 25]), deserves to be developed and tested.
Appendix A: MEGM
The modified extra-gradient method (MEGM) is a projection algorithm to solve the variational inequality problem. It is a revision of the original extra-gradient algorithm, which adds an Armijo rule to update the step-size. MEGM has good global convergence and requires weaker convergence condition [26]. To make MEGM’s projection process more convenient, a RUE model is usually rewritten into an equivalent and closed form as follows.
Find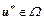 , such that
, such that
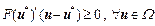 (A1)
(A1)
where
 (A2)
(A2)
In above two equations, superscript ‘′’ is the transposition operator; 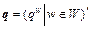 is the travel demand vector; N is total number of paths in the network; M is the number of OD-pairs in the network;
is the travel demand vector; N is total number of paths in the network; M is the number of OD-pairs in the network; 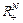 and
and 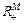 are the non-negative Euclidean spaces with N and M dimensions, respectively; Λ is the path-OD incidence matrix, in which the element equals 1 if a path connects a specified OD-pair and 0, otherwise;
are the non-negative Euclidean spaces with N and M dimensions, respectively; Λ is the path-OD incidence matrix, in which the element equals 1 if a path connects a specified OD-pair and 0, otherwise; 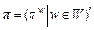 is the Lagrangian multiplier vector of demand conservation constraints, which corresponds to the minimum RM vector between OD-pairs in an economic sense.
is the Lagrangian multiplier vector of demand conservation constraints, which corresponds to the minimum RM vector between OD-pairs in an economic sense.
The procedure of MEGM is stated as follows.
MEGM
Step 0: Choose an initial flow pattern f 0, 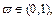
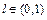 and γ>0, and set n=0;
and γ>0, and set n=0;
Step 1: If f t is the solution, stop; otherwise, set
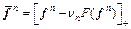 (A3)
(A3)
where  and
and 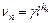 with hn being the minimal non-negative integer meeting
with hn being the minimal non-negative integer meeting
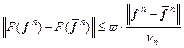 (A4)
(A4)
Step 3: Set
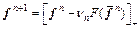 (A5)
(A5)
and n=n+1, and return to Step 1.
Nomenclature
A
Set of links, 
W
Set of OD-pairs, 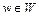
Kw
Set of acyclic paths between OD-pair w, 
Ω1
Set of feasible path flow patterns
n
Swapping time index
α
Travel reliability level
ω
Parameter that reflects traveler’s risk attitude to uncertainty
υ
Weight factor of the combined mean travel time measure
qw
Travel demand between w
θw
Positive constant that reflects the cost sensitivity between w
πw
The minimal RM between w
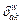
Link-path association indicator, 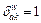 if path k uses link a and
if path k uses link a and 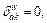 otherwise
otherwise
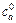
Free-flow travel time of link a
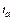
Degradable degree of capacity on link a
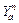
Capacity of link a
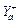
Designed capacity of link a
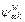
RM indicator on path k between OD-pair w
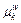
Mean travel time of path k between w
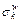
Standard deviation of travel time on path k between w
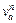
Flow on link a at time n
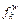
Flow on path k between w

Flow on path k between w at time n
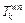
Travel time of path k

Set of paths with RM less than path k, and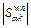 is the number of paths contained in
is the number of paths contained in 

Proportion of flow swapping from path k to path p between w at time n
E(·)
Expectation operator of a random variable
var(·)
Variance operator of a random variable
Φ–1(·)
Inverse of the standard normal distribution function
U(x, y)
Uniform distribution indicator of a random variable with expectation x and standard deviation
References
[1] NIE Yu. Multi-class percentile user equilibrium with flow-dependent stochasticity [J]. Transportation Research Part B, 2011, 45(10): 1641–1659. DOI: 10.1016/j.trb.2011.06.001.
[2] LO H K, TUNG Y K. Network with degradable links: capacity analysis and design [J]. Transportation Research Part B, 2003, 37(4): 345–363. DOI: 10.1016/S0191- 2615(02)00017-6.
[3] CHEN A, ZHOU Z. The alpha-reliable mean-excess traffic equilibrium model with stochastic travel times [J]. Transportation Research Part B, 2010, 44(4): 493–513. DOI:10.1016/j.trb.2009.11.003.
[4] ZHANG Wen-yi, GUAN Wei, SONG Li-ying, SUN Hui-jun. Alpha-reliable combined mean traffic equilibrium model with stochastic travel times [J]. Journal of Central South University, 2013, 20(12): 3770–3778. DOI: 10.1007/s11771-013-1906-z.
[5] BERNSTEIN D, GABRIEL S A. Solving the nonadditive traffic equilibrium problem [M]// PARDALOS P M, HEARN D W, HAGER W W. Network Optimization. New York: Springer, 1997: 72–102.
[6] GABRIEL S A, BERNSTEIN D. The traffic equilibrium problem with nonadditive path costs [J]. Transportation Science, 1997, 31(4): 337–348. DOI: 10.1287/trsc.31.4.337.
[7] HAN De-ren. A modified alternating direction method for variational inequality problems [J]. Applied Mathematics and Optimization, 2002, 45 (1): 63–74. DOI: 10.1007/s00245- 001-0029-3.
[8] XIU Nai-hua, ZHANG Jian-zhong. Some recent advances in projection-type methods for variational inequalities [J]. Journal of Computational and Applied Mathematics, 2003, 152(1): 559–585. DOI: 10.1016/S0377-0427(02)00730-6.
[9] CHEN A, ZHOU Z, XU X D. A self-adaptive gradient projection algorithm for the nonadditive traffic equilibrium problem [J]. Computers and Operations Research, 2012, 39(2): 127–138. DOI: 10.1016/j.cor.2011. 02.018.
[10] MOUNCE R. Convergence in a continuous dynamic queuing model for traffic networks [J]. Transportation Research Part B, 2006, 40(9): 779–791. DOI: 10.1016/j.trb.2005.10.004.
[11] HUANG Hai-jun, LAM W H K. Modeling and solving the dynamic user equilibrium route and departure time choice problem in network with queues [J]. Transportation Research B, 2002, 36(3): 253–273. DOI: 10.1016/S0191- 2615(00)00049-7.
[12] NIE Xiao-jian. The study of dynamic user-equilibrium traffic assignment [D]. Davis: University of California, 2003.
[13] HAN Sang-jin. A route-based solution algorithm for dynamic user equilibrium assignments [J]. Transportation Research Part B, 2007, 41(10): 1094–1113. DOI: 10.1016/ j.trb.2007.05.001.
[14] CHEN Bi-yu, LAM W H K, SUMALEE A, SHAO Hu. An efficient solution algorithm for solving multi-class reliability-based traffic assignment problem [J]. Mathematical and Computer Modelling, 2011, 54: 1428–1439. DOI: 10.1016/j.mcm.2011.04.015.
[15] MOUNCE R, CAREY M. On the convergence of the MSA for calculating equilibrium in traffic networks [J]. Transportation Science, 2015, 49(3): 535–542. DOI: 10.1287/trsc.2014.0517.
[16] MOUNCE R, CAREY M. Route swapping in dynamic traffic networks [J]. Transportation Research B, 2011, 45(1): 102–111. DOI:10.1016/j.trb.2010.05.005.
[17] SMITH M J. The stability of a dynamic model of traffic assignment–An application of a method of Lyapunov [J]. Transportation Science, 1984, 18(3): 259–304. DOI: 10.1287/trsc.18.3.245.
[18] SHEFFI Y. Urban transportation networks: Equilibrium analysis with mathematical programming methods [M]. Englewood Cliffs: Prentice-Hall, 1985.
[19] CAREY M, GE Ying-en. Comparison of methods for path flow reassignment for dynamic user equilibrium [J]. Networks and Spatial Economics, 2012, 12(3): 337–376. DOI: 10.1007/s11067-011-9159-6.
[20] RASMUSSEN T K, WATLING D P, PRATO C G, NIELSEN O A. Stochastic user equilibrium with equilibrated choice sets: Part II–Solving the restricted SUE for the logit family [J]. Transportation Research Part B, 2015, 77: 146–165. DOI: 10.1016/j.trb.2015.03.009.
[21] ZHANG Wen-yi, GUAN Wei, MA Ji-hui, TIAN Jun-fang. A nonlinear pairwise swapping dynamics to model the selfish rerouting evolutionary game [J]. Networks and Spatial Economics, 2015, 15(4): 1075–1092. DOI: 10.1007/s11067- 014-9281-3.
[22] FOSGERAU M, KARLSTROM A. The value of reliability [J]. Transportation Research Part B, 2010, 44(1): 38–49. DOI: 10.1016/j.trb.2009.05.002.
[23] PATRIKSSON M. The traffic assignment problem: Models and methods [M]. Utrecht: VSP, 1994.
[24] NAGURNEY A. Network economics: A variational inequality approach [M]. Dordrecht: Kluwer Academic Publishers, 1993: 14–15.
[25] PANG Xin-fu, GAO Liang, PAN Quan-ke, TIAN Wei-hua, YU Sheng-ping. A novel Lagrangian relaxation level approach for scheduling steelmaking-refining-continuous casting production [J]. Journal of Central South University, 2017, 24(2): 467–477. DOI: 10.1007/s11771-017-3449-1.
[26] HAN Ji-ye, XIU Nai-hua, QI Hou-duo. Nonlinear complementarity theory and algorithms [M]. Shanghai: Shanghai Scientific & Technical Publishers, 2006: 132–141. (in Chinese)
(Edited by YANG Hua)
中文导读
求解可靠性用户均衡的自调节对向调整算法
摘要:因可靠性测度(RM)不满足单调性,数学规划算法在求解可靠性用户均衡(RUE)问题时通常效率较低。相比之下,调整算法因不依赖于导数信息且单调性要求较弱,为搜求RUE提供了一种简单方便的备选方案。然而,既有调整算法通常基于线性调整过程,无法自然规避过度调整问题,且其步长参数的更新也未考虑调整过程的特性,为此,本文提议一种自调节对向调整算法(SRPSA)来搜求RUE,该算法由RM对向调整过程(RMPSP)、步长参数自降算子和收敛准则三部分构成,迭代过程中无需检验中间解和步长参数的可行性。数值结果显示,SRPSA中的步长参数自降算子有效,并且算法可迅速搜寻到近似可靠性用户均衡。因此,SRPSA可为其他局部优化算法提供优秀的初始解方案。
关键词:旅行时间可靠性;可靠性用户均衡;日变动态;路径调整
Foundation item: Projects(71601015, 71501013, 71471014) supported by the National Natural Science Foundation of China; Project(2015JBM060) supported by the Fundamental Research Funds for the Central Universities, China
Received date: 2017-03-27; Accepted date: 2017-09-24
Corresponding author: ZHANG Wen-yi, PhD, Lecturer; Tel: +86-10-51688514; E-mail: wyzhang@bjtu.edu.cn; ORCID: 0000-0002- 4752-9994
Abstract: The violation of monotonicity on reliability measures (RMs) usually makes the mathematical programming algorithms less efficient in solving the reliability-based user equilibrium (RUE) problem. The swapping algorithms provide a simple and convenient alternative to search traffic equilibrium since they are derivative-free and require weaker monotonicity. However, the existing swapping algorithms are usually based on linear swapping processes which cannot naturally avoid overswapping, and the step-size parameter update methods do not take the swapping feature into account. In this paper, we suggest a self-regulating pairwise swapping algorithm (SRPSA) to search RUE. SRPSA comprises an RM-based pairwise swapping process (RMPSP), a parameter self-diminishing operator and a termination criterion. SRPSA does not need to check the feasibility of either solutions or step-size parameter. It is suggested from the numerical analyses that SRPSA is effective and can swap to the quasi-RUE very fast. Therefore, SRPSA offers a good approach to generate initial points for those superior local search algorithms.


