Trans. Nonferrous Met. Soc. China 25(2015) 241-248
Phase-field modeling of dendritic growth under forced flow based on adaptive finite element method
Chang-sheng ZHU1,2, Peng LEI1, Rong-zhen XIAO2, Li FENG2
1. College of Computer and Communication, Lanzhou University of Technology, Lanzhou 730050, China;
2. State Key Laboratory of Advanced Processing and Recycling of Non-ferrous Metals, Lanzhou University of Technology, Lanzhou 730050, China
Received 24 February 2014; accepted 26 June 2014
Abstract:
A mathematical model combined projection algorithm with phase-field method was applied. The adaptive finite element method was adopted to solve the model based on the non-uniform grid, and the behavior of dendritic growth was simulated from undercooled nickel melt under the forced flow. The simulation results show that the asymmetry behavior of the dendritic growth is caused by the forced flow. When the flow velocity is less than the critical value, the asymmetry of dendrite is little influenced by the forced flow. Once the flow velocity reaches or exceeds the critical value, the controlling factor of dendrite growth gradually changes from thermal diffusion to convection. With the increase of the flow velocity, the deflection angle towards upstream direction of the primary dendrite stem becomes larger. The effect of the dendrite growth on the flow field of the melt is apparent. With the increase of the dendrite size, the vortex is present in the downstream regions, and the vortex region is gradually enlarged. Dendrite tips appear to remelt. In addition, the adaptive finite element method can reduce CPU running time by one order of magnitude compared with uniform grid method, and the speed-up ratio is proportional to the size of computational domain.
Key words:
dendritic growth; phase-field model; forced flow; adaptive finite element method;
1 Introduction
Dendrite is a form of most casts during solidification. The dendrite growth is a complex physical process influenced by the transfer of heat, mass and momentum. The transfer of heat and mass in the process of solidification not only depends on the diffusion, but also closely relates to the flow of liquid metal. The macro-segregation, solidification shrinkage cavity and cast defects are influenced dramatically by the melt flow, and those factors restrain the performances of metal materials.
In recent years, on the basis of pure diffusion phase- field model, the numerical simulation has provided a very convenient and effective method for the study of microstructures evolution [1-5]. TONG et al [6] and BECKERMANN and SUN [7] used phase-field method combined with SIMPLE algorithm to study the relationship between dendritic tip morphology of pure material and liquid fluid velocity. Finite difference method and SIMPLE algorithm were adopted to solve phase-field and flow field, respectively. The effects of flow velocity on the unsymmetrical dendritic growth and the temperature distribution were investigated numerically based on the phase-field model [8]. CHEN and CHEN [9] reported the phase-field model coupled with the flow field to simulate two-dimensional dendrite growth of metal by using finite difference method, and the effect of flow velocity on metal dendritic crystal growth was investigated. Based on the Wheeler model, a phase-field model was proposed by coupling with concentration field, temperature field and flow field. An explicit finite difference numerical method was used to solve the phase-field model [10,11].
However, the adaptive finite element method based on non-uniform grid is more efficient and less amount of calculation than the method based on uniform grid [12,13]. When the mass and momentum conservation equations are calculated, projection method has the high efficiency through prediction and correction step to get the speed and pressure at the new time [14].
Based on the Wheeler diffusion model, a phase-field model incorporated both flow and thermal noise was proposed in this study, and the effect of gravity and dynamics was neglected. The adaptive finite element algorithm [15,16], the functional library AFEPack [17] and the projection algorithm [18] were employed to solve the phase-field model, momentum and mass conservation equations. The dendritic growth of nickel was simulated quantitatively, and the effects of flow velocity on the dendrite morphology and tip operating state were investigated. In addition, the influence of the dendrite growth on the fluid flow was studied.
2 Simulation model
2.1 Dimensionless 2D phase-field model equations
Phase-field model represents the system’s physical state of each point by introducing a continuous order parameter φ. In this study, φ=0 represents the solid condition, φ=1 represents the liquid condition, and 0<φ<1 represents solid-liquid interface. The phase-field model equation is defined by [19]
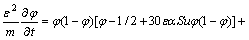
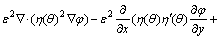
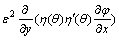(1)
The form of thermal noise in Eq. (1) is given by [20]
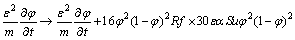(2)
where ε stands for the thickness of interfacial layer, and α is defined as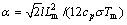 
. The dimensionless temperature u is given by
, Tm is the melting temperature, and T0 is the initial temperature of system. Dimensionless supercooling degree S is defined as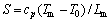 
, cp is the heat capacity at constant pressure, and Lm is the latent heat, interfacial migration coefficient m is defined by m=μσTm/(κLm), μ denotes the interface migration rate, σ represents the interface energy, and κ stands for the thermal diffusivity. The anisotropic factor is defined by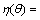
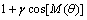, γ represents the anisotropy strength, M denotes the mode of anisotropic, and θ reflects the angle between the preferred orientation of solidification and the positive direction of x axis. Moreover, 
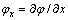and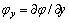
. Applying l as the length scale and 
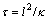as the time scale, all dimensional variables are cast into their dimensionless forms. 
is the random number, and f is the thermal noise intensity.
2.2 Thermal field equation coupled with flow field
The thermal field equation takes the following form [21]:
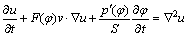(3)
where v stands for the dimensionless flow velocity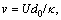 
U stands for the initial flow velocity, and interpolation function F(φ) is given by
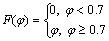(4)
In Eq. (3), p′(φ) is defined as the derivative of potential function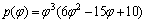 
for φ [19].
2.3 Conservation equations of mass and momentum
The conservation equations for mass and momentum take the following forms [22]:
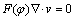(5)
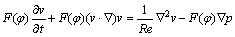(6)
where p is the dimensionless pressure, and Re denotes Reynolds number.
3 Numerical simulation parameters and methods
3.1 Initial condition and boundary condition
An initial nucleus of the radius r0 can be defined as
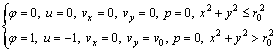(7)
where x and y are the coordinate axes, vx and vy are the convection velocities along axes x and y, respectively. The supercooled melt enters the domain from the top boundary with a uniform velocity v0 and exits at the bottom boundary. The Zero-Neumann boundary conditions are imposed at the boundaries of the computational domain for phase field and thermal field, while the mass and momentum equations employed no-slip boundary conditions. The initial condition of simulation domain is shown in Fig. 1. The simulation domain size dimensions 4.0l×4.0l (l=1.33×104d0), where d0 is the capillary length.
The material parameters of phase-field model are shown in Table 1.
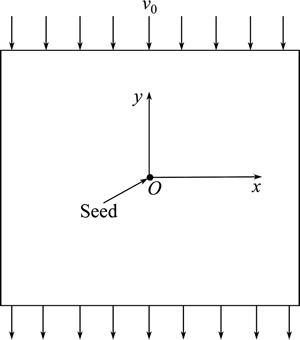
Fig. 1 Initial condition of simulation domain
Table 1 Physical parameters of pure Ni
3.2 Numerical simulation methods
3.2.1 Adaptive finite element method
According to the adaptive finite element method, the partial differential Eqs. (1) and (3) should be transformed into the corresponding week forms. The trial functions v1(x, y) and z(x, y) are introduced. The time domain is dispersed by using the time interval △t. According to Green’s theorem, the weak forms of Eqs. (1) and (3) are defined by
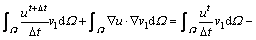
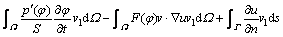(8)
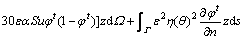(9)
3.2.2 Efficiency of adaptive finite element method
The results of solving phase field model based on adaptive finite element method are shown in Fig. 2, where the domain dimensions are 3.0l×3.0l. Figure 2(a) shows the initial mesh and Fig. 2(b) shows the dendrite morphology at t=6900△t. Figure 2(c) shows the amplified result of box in Fig. 2(b). It can be found that, the grids are refined in region A close to the solid-liquid interface, and the grids are coarsened in regions B, C and D far away from the interface. The number of the nodes is just 2.79×105 by using adaptive finite element method, which is less than 1.6×106 by using the uniform grid method at the termination of the calculation [12]. So, the adaptive finite element method reduces the computational cost and improves the computational efficiency dramatically.
Fig. 2 Graphs of grid subdivision
Table 2 Relationship among CPU running time, speed-up ratio and domain size of system
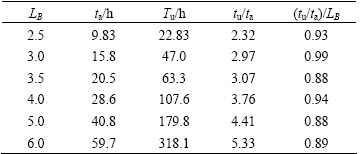
The relationship among the CPU running time, speed-up ratio and computational domain size is shown in Table 2, where ta represents the CPU running time of adaptive finite element method, tu stands for the CPU running time of uniform grid method, and LB denotes the computational domain size of the system. The functional relationship between the CPU running time and the computational domain size is given by
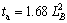(10)
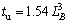(11)
The functional relationship between the speed-up ratio and the computational domain size is defined by
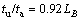(12)
Time complexities of adaptive finite element method and uniform grid method are
and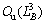 
, respectively. What’s more, the speed-up ratio 
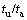is proportional to the domain size. By using the non-uniform grid adaptive finite element method, the greater the computational domain size is, the higher computational efficiency is.
3.2.3 Projection algorithm
The mass and momentum equations were solved numerically by using the fractional-step projection algorithm [18]. As the fractional-step projection algorithm can get higher computational efficiency in solving incompressible Navier-Stokes equations, the algorithm has been more and more widely used [23].
To guarantee unconditional stability and avoid any restriction on the time step, the advection term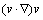 
in Eq. (6) is replaced by its skew-symmetric form 
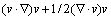, and the advection–diffusion step is given by [18,21]
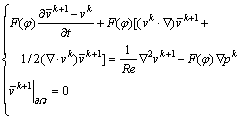(13)
The projection step is taken by the following incremental form:
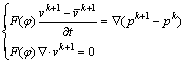(14)
The Poisson equation for the pressure increment is given by
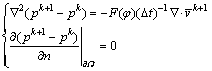(15)
where 
stands for the intermediate velocity, and vk+1 denotes divergence-free velocity field. The velocity field and pressure field are updated by
(16)
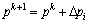(17)
4 Results and discussion
4.1 Dendrite morphologies at different flow velocities
Figure 3 shows the dendrite morphologies and thermal distribution at t=6500△t, where the thermal noise intensity f=2.0. It can be seen from Fig. 3 that, the dendrite grows symmetrically without forced flow (Fig. 3(a)), and the thermal diffusion layer distributes symmetrically as well (Fig. 3(c)). Figures 3(b) and (b) show the dendritic morphology and the thermal diffusion layer distribution with flow velocity of v=0.0026. Dendrite shapes show asymmetry, and the growth rates of dendrites are different in preferentially growing directions. The main dendrite arm in the upstream region is longer and wider compared with the main dendrite arm in the downstream. Due to the erosion of convection effect on upstream dendrite, it reduces the thickness of thermal diffusion layer and leads to high temperature gradient, and the release of latent heat is propitious. The actual undercooling is increscent and the dendrite grows up quickly. Therefore, the development of primary dendrite and secondary dendrite arms is promoted.
In downstream region, the diffusion layer of the dendrite tip is thinner and the temperature gradient is higher without forced flow, as shown in Fig. 3(c). In the case of forced flow, the thermal diffusion layer of the dendrite tip is thicker than the former situation, as shown in Fig. 3(d). In addition, the temperature gradient and the actual undercooling are low, thus the dendrite growth velocity is slow. The thermal diffusion layer prevents the release of the latent heat, so the disturbance of interface is restrained. At horizontal direction, the growth velocity of the dendrite lies between the middle of downstream region and upstream region.
4.2 Relationship between forced flow and dendrite growth
4.2.1 Effect of forced flow on dendrite growth
The effect of forced flow on the growth velocities of upstream, normal and downstream dendrites is obvious. Figure 4 shows the dendrite shape at growth time of t=6500△t and the initial flow velocities v=0, 0.0011, 0.0025, 0.0026 and 0.0036, respectively, where the supercooling degree is S=0.65.
It can be found that, the primary dendrites do not shrink dramatically in the downstream region when the flow velocity is less than 0.0026. The effect of forced flow on the dendrite morphology is slight when the flow velocity is low, and the dendrite growth is mainly controlled by thermal diffusion. With the increase of flow velocity, the dendrite growth process is controlled by the convection gradually. On one hand, the growth rate of primary dendrites in upstream region increases with the increase of the flow velocity, and the primary dendrites and side-branches become more and more developed. On the other hand, the growth rate of main dendrites in downstream region reduces with the increase of the flow velocity, and the growth of the main branches and side-branches is restrained strongly in this region.
Fig. 3 Dendrite morphologies (a, b) and thermal diffusion layer distribution (c, d) of phase-field modeling at t=6500△t
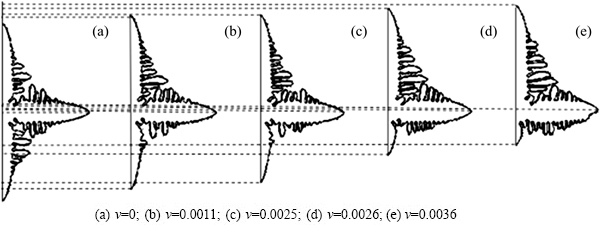
Fig. 4 Effect of flow velocity on morphologies of main branches at t=6500△t
Figure 5 shows the dendrite shape and deflection angle of the horizontal dendritic tip under different flow velocities at t=6500△t. It can be seen that, the morphology of the dendrite is symmetric completely without forced flow, as shown in Fig. 5(a), and the deflection angle of the horizontal dendritic tip is 0°. The horizontal dendrite tip deviates the horizontal line towards the fluid direction under the condition of forced flow. With the increase of forced flow velocity, the deflection angle increases, as shown in Figs. 5(b), (c) and (d).
4.2.2 Effect of dendrite growth on flow field
Figure 6 shows the flow field distribution and grids of temperature field of the dendritic tips at v=0.0036 and t=6500△t, 6100△t, 6900△t, respectively. The position and direction of the arrow represent fluid particle position and flow direction, and the length of the arrow stands for the velocity of fluid particle. It can be seen that, arrows change their directions when the fluid passes the normal direction of the main dendritic tip. The length of arrows is the longest near the primary dendrites, and the flow velocity is the largest in this region. When the dendrite size is small, the vortex does not appear, as shown in Fig. 6(a). With the increase of the dendrite size, the rotation of the small arrows is present in the downstream region, as shown in Fig. 6(b), and the vortex area increases gradually, as shown in Fig. 6(c).
According to the fluid mechanics, the negative pressure becomes stronger gradually in the downstream region, and the flow of the melt in the vortex region leads to the change of thermal distribution near the dendritic tips, as shown in Figs. 6(e) and (f). The latent heat gathered in this region makes the actual temperature at the vortex region higher than the melting point of the melt, and the remelting of the dendrite occurs.
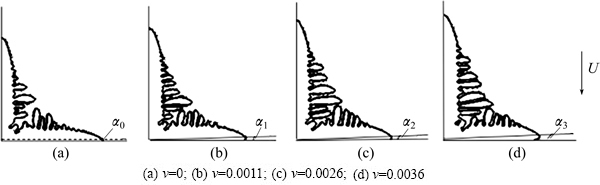
Fig. 5 Effect of flow velocity on deflection angle of horizontal dendritic tip flow at t=6500△t
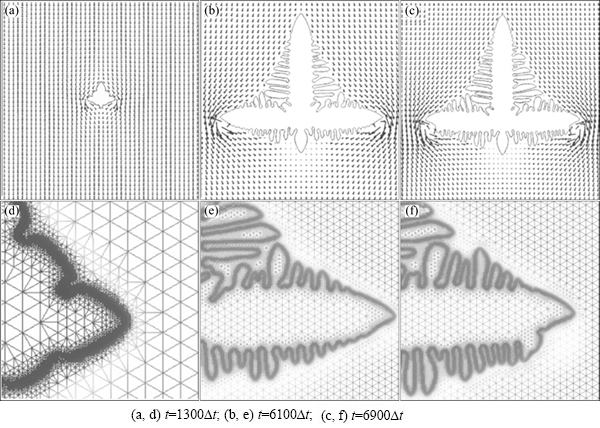
Fig. 6 Flow field distribution and grids of temperature field at v=0.0036 and different growth time
5 Conclusions
1) A phase-field model of pure material combined with the projection algorithm is applied to simulating dendrite growth under the condition of forced flow. The phase-field model is solved by using the efficient adaptive finite element method. The computational cost is reduced by an order of magnitude by using the non-uniform grid, and the computational efficiency is improved dramatically.
2) When the flow velocity is low, the effect of the forced flow on the dendrite morphology is slight. But the symmetry of dendrite shape is collapsed obviously with the increase of the flow velocity. The main dendrite arms in the upstream region are more developed than those in the downstream region, and the side-branches are developed as well in the upstream region. The horizontal dendritic tip deviates the horizontal line under the condition of the forced flow.
3) The effect of the dendrite growth on the flow field is evident. With the increase of dendrite size, the vortex is present in the downstream regions. The actual temperature is higher than the melting point of the melt in the vortex region, and the remelting of the dendrite occurs.
References
[1] YUAN L, LEE D P. Dendritic solidification under natural and forced convection in binary alloys: 2D versus 3D simulation [J]. Modeling and Simulation in Materials Science and Engineering, 2010, 18(5): 055008-055020.
[2] WANG Z P, WANG J W, ZHU C S, FENG L, XIAO R Z. Phase-field simulations of forced flow effect on dendritic growth perpendicular to flow [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(3): 612-617.
[3] WANG J W, ZHU C S, WANG Z P, FENG L, XIAO R Z. Phase-field simulation of forced flow effect on random preferred growth direction of multiple grains [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(7): 1620-1626.
[4] WANG J W, WANG Z P, LU Y, ZHU C S, FENG L, XIAO R Z. Effect of forced lamina flow on microsegregation simulated by phase field method quantitatively [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 391-397.
[5] ZHU C S, XIAO R Z, WANG Z P. Numerical simulation of recalescence for a binary alloy using phase-field approach [J]. Transactions of Nonferrous Metals Society of China, 2009, 19(5): 1286-1293.
[6] TONG X, BECLERMANN C, KARM A A, LI Q. Phase-field simulations of dendritic crystal growth in a forced flow [J]. Physical Review E, 2001, 63(6): 061601.
[7] BECKERMANN C, SUN Y. Effect of solid-liquid density change on dendrite tip velocity and shape selection [J]. Journal of Crystal Growth, 2009, 311(19): 4447-4452.
[8] ZHU C S, WANG J W, WANG Z P, FENG L. Dendritic growth in forced flow using the phase-field simulation [J]. Acta Physica Sinica, 2010, 59(10): 7317-7423. (in Chinese)
[9] CHEN Y J, CHEN C L. Simulation of the influence of convection velocity on upstream dendritic growth using phase-field method [J]. Acta Physica Sinica, 2008, 57(7): 4585-4589.
[10] YUAN X F, DING Y T, GUO T B, HU Y, TANG X Q. Phase-field method of dendritic growth under convection [J]. The Chinese Journal of Nonferrou Metals, 2010, 20(4): 681-687. (in Chinese)
[11] YUAN X F, DING Y T, GUO T B, HU Y. Numerical simulation of dendritic growth of magnesium alloys using phase-field method under forced flow [J]. The Chinese Journal of Nonferrous Metals, 2010, 20(8): 1474-1480. (in Chinese)
[12] CHEN Y, KANG X H, LI D Z. Phase-field modeling of free dendritic growth with adaptive finite element method [J]. Acta Physica Sinica, 2009, 58(1): 390-397. (in Chinese)
[13] PROVATAS N, GOLDENFELD N, DANTZIG J. Adaptive mesh refinement computation of solidification microstructures using dynamic data structures [J]. Journal of Computational Physics, 1999, 148: 265-290.
[14] LIU M E, REN Y X, ZHANG H X. Review on the projection methods in the numerical solution of the incompressible flow [J]. Advances in Mechanics, 2006, 36(4): 591-598. (in Chinese)
[15] LI R. On multi-mesh H-adaptive methods [J]. Journal of Scientific Computing, 2005, 24(3): 321-341.
[16] HU X L, LI R, TANG T. A multi-mesh adaptive finite element approximation to phase field models [J]. Communications in Computational Physics, 2009, 5(5): 1012-1029.
[17] LI R, LIU W B. AFEPack [EB/OL]. http://circus.math. pku.edu.cn/AFEPack. [2013-6-5].
[18] GUERMOND J L, QUARTAPELLE L. On stability and convergence of projection methods based on pressure Poisson equation [J]. International Journal for Numerical Methods in Fluids, 1998, 26: 1039-1053.
[19] WANG S L, SEKWEKA R F, WHEELER A A, MURRAY B T, CORIELL S R, BRAUNC J, MCFADDEC G B. Thermo dynamically-consistent phase-field models for solidification [J]. Physica D: Nonlinear Phenomena, 1993, 69(1): 189-200.
[20] LIU J, SU Y K, XUN G A. Effects of phase-field parameters on dendritic morphology using phase field simulation [J]. Journal of Shandong University: Engineering Science, 2007, 37(3): 74-77. (in Chinese)
[21] CHEN Y. Quantitative phase-field modeling of the microstructure evolution of primary phase and experimental validations during solidification of metals [D]. Shenyang: Institute of Metal Research, Chinese Academy of Sciences, 2012: 90-110. (in Chinese)
[22] BECKERMANN C, DIEPERS H J, STEINBACH I, KARMA A, TONG X. Modeling melt convection in phase-field simulations of solidification [J]. Journal of Computational Physics, 1999, 154: 468-496.
[23] LIU M E. Projection methods for numerically solving incompressible flow [D]. Beijing: Tsinghua University Press, 2004: 14-40. (in Chinese).
基于自适应有限元相场模型模拟强制流动条件下的枝晶生长
朱昶胜1,2，雷 鹏1，肖荣振2，冯 力2
1. 兰州理工大学 计算机与通信学院，兰州 730050；
2. 兰州理工大学 有色金属先进加工与再利用国家重点实验室，兰州730050
摘 要：应用投影算法与相场法相结合的数学模型，采用基于非均匀网格的自适应有限元法求解该模型，并对强制流动作用下镍过冷熔体中枝晶生长行为进行模拟。模拟结果表明，强迫对流的引入导致枝晶生长的不对称性。当流速小于临界值时，流动对枝晶的不对称生长影响较小；当流速达到或超过临界值时，枝晶生长的控制因素逐渐从热扩散过渡到对流。随着流速的增大，流动法向的一次枝晶臂朝逆流方向倾斜角度增大。而枝晶生长对熔体流动具有明显的影响。随着枝晶尺寸的增大，在顺流区域产生涡流效应，涡流区逐渐扩大并在枝晶尖端出现重熔现象。此外，非均匀网格的自适应有限元方法的CPU耗费时间比均匀网格方法降低一个数量级，并且加速比与计算域尺寸成正比。
关键词：枝晶生长；相场模拟；强制流动；自适应有限元法
(Edited by Wei-ping CHEN)
Foundation item: Projects (51161011, 11364024) supported by the National Natural Science Foundation of China; Project (1204GKCA065) supported by the Key Technology R&D Program of Gansu Province, China; Project (201210) supported by the Fundamental Research Funds for the Universities of Gansu Province, China; Project (J201304) supported by the Funds for Distinguished Young Scientists of Lanzhou University of Technology, China
Corresponding author: Chang-sheng ZHU; Tel: +86-18189665818; E-mail: 867320505@qq.com
DOI: 10.1016/S1003-6326(15)63599-3
Abstract: A mathematical model combined projection algorithm with phase-field method was applied. The adaptive finite element method was adopted to solve the model based on the non-uniform grid, and the behavior of dendritic growth was simulated from undercooled nickel melt under the forced flow. The simulation results show that the asymmetry behavior of the dendritic growth is caused by the forced flow. When the flow velocity is less than the critical value, the asymmetry of dendrite is little influenced by the forced flow. Once the flow velocity reaches or exceeds the critical value, the controlling factor of dendrite growth gradually changes from thermal diffusion to convection. With the increase of the flow velocity, the deflection angle towards upstream direction of the primary dendrite stem becomes larger. The effect of the dendrite growth on the flow field of the melt is apparent. With the increase of the dendrite size, the vortex is present in the downstream regions, and the vortex region is gradually enlarged. Dendrite tips appear to remelt. In addition, the adaptive finite element method can reduce CPU running time by one order of magnitude compared with uniform grid method, and the speed-up ratio is proportional to the size of computational domain.
