Article ID: 1003-6326(2005)02-0323-05
Magnetoresistance and magnetization of La2/3(Ca0.60Ba0.40)1/3MnO3 in different temperature ranges
GAI Rong-quan(盖荣权)1, HUANG Zhi-gao(黄志高)1, 2, LAI Heng(赖 恒)1,
CHEN Shui-yuan(陈水源)1, DU You-wei(都有为)2
(1. Department of Physics, Fujian Normal University, Fuzhou 350007, China;
2. National Laboratory of Solid State Microstructures, Nanjing University, Nanjing 210093, China)
Abstract:
A polycrystalline La2/3(Ca0.60Ba0.40)1/3MnO3 was prepared by standard solid reaction method. Magnetization(M) and magnetoresistance of the sample were measured between T=77K and 350K. It is found that some correlations exist in the external field dependency of the magnetoresistance magnetoresistance and M in the low and high temperature regions. Moreover, there are different magnetic field dependence of magnetoresistance and magnetization in different temperature ranges, which indicates the presence of different magnetoresistance mechanisms. Based on the models of spin-polarized tunneling and percolation model, the simulated magnetoresistance obtained using Monte Carlo method well explains the experimental fact.
Key words:
magnetoresistance; magnetization; manganese perovskite; Monte Carlo method CLC number: O482.5;
Document code: A
1 INTRODUCTION
The colossal magnetoresistance(CMR) of Re1-xMexMnO3(Re=La, Y, Me=Ca, Ba, Sr, Pb, K) with perovskite structure has drawn considerable interest[1, 2]. Much theoretical and experimental work has been done to study the physical mechanism of CMR effect. There are two distinct CMR effects in polycrystalline materials: the first one is the low-temperature CMR that increases with decreasing temperature, which is attributed to the spin polarized tunneling through a magnetic barrier in the grain boundaries[3-12]. In order to explain the tunneling magnetoresistance of the nanostructured materials, a two-level model of tunneling magnetoresistance containing co-play of the relative orientation of moments between clusters, the intrinsic characters of clusters, Coulomb blockade effect, was suggested in our previous work[13]. It is found that the unusual enhancement of magnetoresistance is due to the interaction between the clusters and the intrinsic characters of clusters coating the complex surface. Especially, it is thought that the coating surface of the cluster or the interface between the clusters plays an important role for the enhancement of magnetoresistance. Another one is CMR near the ferromagnetic ordering temperature, which have been explained by several theories, such as percolative phase separation[14-17], the double exchange model with the Jahn-Teller effect[18], the double exchange model with the non-magnetic disorder[19] and the double exchange model with spin-disorder scattering[20, 21]. In the percolation model, it is assumed that the sample consists of ferromagnetic metallic particles with a volume fraction randomly distributed over the paramagnetic insulating matrix, and the simulated results suggest that the percolation of FMM domains is responsible for the observed insulator-metal transition[16]. The complex magnetic field dependence of magnetoresistance, especially the low-field magnetoresistance (LFMR) and the high-field magnetoresistance (HFMR) at the low-temperature, has also been an interesting topic due to the importance in the understanding of CMR mechanism and applications[5,22-24]. However, up to now, the underlying CMR mechanisms are still unclear. In this paper, the temperature and field dependence of the resistivity and magnetoresistance of polycrystalline sample were studied. Based on the double exchange model with spin-disorder scattering, spin-polarized tunneling effect and Monte Carlo simulation, the magnetoresistances as function of temperature and magnetic field were obtained, which well explain the experimental results.
2 EXPERIMENTAL
Polycrystalline sample La2/3(Ca0.60Ba0.40)1/3-MnO3 was fabricated using a standard solid state reaction method. The mixed La2O3, CaCO3, BaCO3 and MnO2 powers in stoichiometric proportions were ground with an automated mortar at different velocities for 24h and preheated at 1000℃ for 10h. Then they were reground at low velocity for 24h, pressed into pellets, sintered at 1290℃ for 24h. The structures of the materials were analyzed by means of X-ray diffractometry (XRD) with CuKα. Resistivity and magnetoresistance were measured by a standard four-probe in the temperature range of 77-400K from zero field up to 1.2T. Magnetization was performed using VSM.
3 RESULTS AND DISCUSSION
Fig.1 shows the magnetization and magnetoresistance as a function of temperature for the sample. From Fig.1, it is found that magnetoresistance increases evidently with decreasing temperature for T〈250K, which is attributed to the spin polarized tunneling through a magnetic barrier. A maximum magnetoresistance of 8% is also observed at Tp=295K. Tp is a transition temperature between metal and insulator phases[1, 2]. From the thermal magnetization, the Curie temperature of the sample is found to be Tc=303K, which is near the value of Tp. The hysteresis loops of the sample at different temperatures are shown in Fig.2. It can be seen that, at low temperature as T〈Tc(303K), a strong ferromagnetic state with small coercivity exists; while at higher temperature as T>Tc, a linear magnetization curve is found, which means the existence of a paramagnetic state. In order to establish the relation between the magnetoresistance magnitude and magnetization, the formula ρ(M)/ρ(0)∝exp[-c(M/Ms)2] or ρ(M)∝1-M2, has been considered[20]. Fig.3 shows the the square of magnetization and magnetoresistance as a function of the external magnetic field at different temperatures for La0.67(Ca0.6Ba0.4)0.33MnO3. It can be seen that at T>Tc, magnetoresistance vs H curve is the same as -M2 vs H, which means ρ(M)∝(1-M2). However, as T is near Tc, ρ(M)—H curve starts to deviate from the M2 relation. When T is below Tc, the deviation from the M2 relation becomes more obvious, which means that different magnetoresistance mechanisms may be obeyed in different ranges of temperature. In addition, as temperature is far below Tc, LFMR and HFMR are observed. It is considered that the LFMR is attributed to the relative orientation of moments between the magnetic clusters, while the HFMR results from the disordered spin scattering in the boundary region.
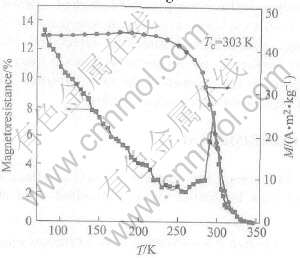
Fig.1 Magnetization and magnetoresistance as function of temperature for sample
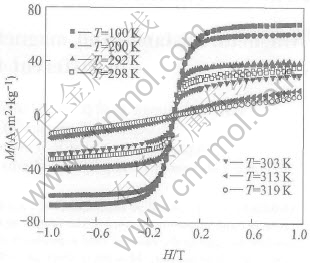
Fig.2 Hysteresis loops of sample at different temperatures
Fig.4(a) shows the temperature dependence of the percolative, tunneling and total resistivity with H=0 for La0.67(Ca0.6Ba0.4)0.33MnO3 sample. The temperature dependence of the percolative and total resistivity with H=0, 0.4T and the calculated percolative magnetoresistance for La0.67(Ca0.6-Ba0.4)0.33MnO3 sample is shown in Fig.4(b). Here, the total resistivity is the measured result, and the percolative and tunneling ones are fitted results, which will be discussed in the latter. The double-peak resistivity-temperature ( ρ vs T) curve in Fig.4 is similar to other experimental results[1-10]. For the film and single crystalline of manganese perovskite, only single peak is found in ρ vs T curves[3].
Based on the recent studies on the tunneling magnetoresistance model in the nanostructured materials[13] and percolation model near Curie temperature[13-16], we construct the percolative structure containing ferromagnetic metallic (FMM) clusters and antiferromagnetic (or paramagnetic) insulating (AFI) matrix as seen in Fig.5(a) and spin-tunneling model between the near clusters consisting of complex spin configurations.
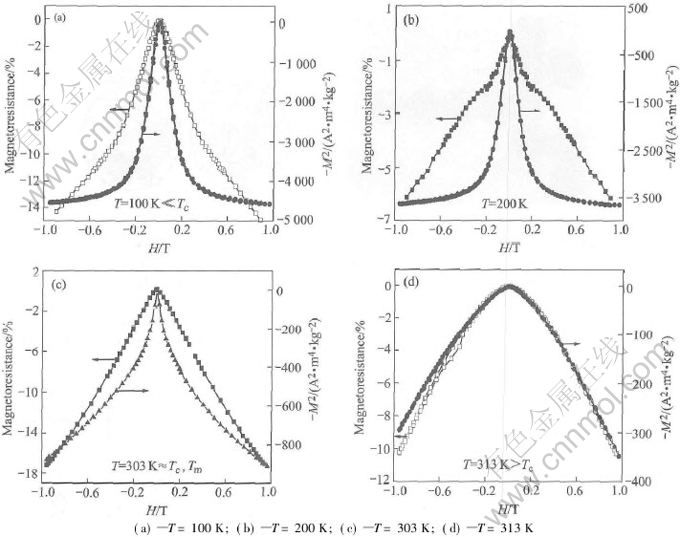
Fig.3 Magnetoresistance and square of magnetization as function of
external magnetic field for La0.67(Ca0.6Ba0.4)0.33MnO3
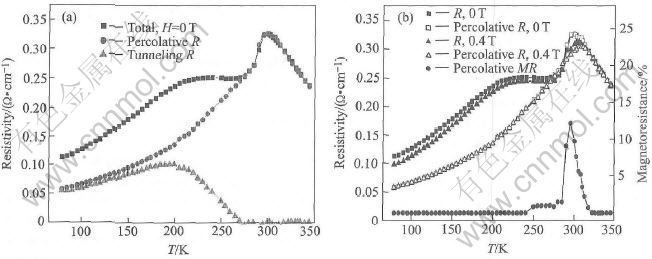
Fig.4 Temperature dependence of percolative, tunneling and total resistivity at H=0T(a),
calculated percolative resistivity and magnetoresistance for sample(b)
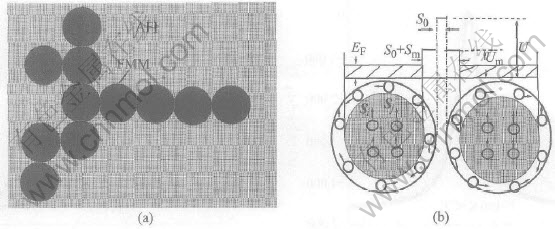
Fig.5 Percolative structure containing ferromagnetic metallic clusters and
antiferromagnetic (or disordered) insulating matrix(a) and
spin-tunnelng schematic illustration between near clusters(b)
For a two-phase system (FMM and AFI phases), we can calculate transport properties of compositionally disordered system containing insulators and conductors using percolation theory. It is assumed that the number fraction of FMM clusters is p. With the similar calculated method in Ref.[16], we can derive the value of p from the reduced magnetization curve as seen in Fig.1. For a 20×20 2D lattice with periodic boundary condition, we also can calculate the probability (f) in which the system with number fraction (p) of FMM clusters is in a conducting state by Monte Carlo simulation. It is assumed that the resistivities of the pure FMM and AFI phases are RM and RI, respectively. Then the resistivity of the system can be described as: RP=(1-f)RI+fRM. Here, RI corresponds to the Motts variable range hopping resistivity for T>Tc[25]. From the data of resistivity in Fig.4, we can get
RI=5.5×10-7exp[4.5×106/T]1/4(1)
Also, from the best data fitting for the peak of the resistivity in Fig.4(a), we obtain
RM= 0.00436+2.29×10-7T2(2)
Thus we can get the percolative resistivity at H=0 and 0.4T, and the magnetoresistance curve near Tc can be calculated, as found in Fig.4(b). Another resistivity coming off the total resistivity is also found in Fig.4(a), which is thought as the tunneling one.
The tunneling resistivity can be expressed by[13]
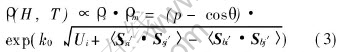
where the first term ρs results from the relative orientation of moments between the magnetic clusters, the second one ρm is associated with the intrinsic characters of clusters, the definition of the parameters in Eqn.(3) are found in Ref.[13]. Based on the reduced double exchange model with antiferromagnetic superexchange coupling and a magnetic field, Hamiltonian can be given as[26]
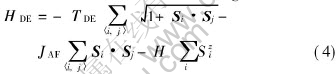
According to Eqns.(3), (4) and combining with Monte Carlo simulation procedure in Ref.[13], we can obtain the temperature dependence of the simulated tunneling magnetoresistance as seen in Fig.6. Fig.6 shows the temperature dependence of the simulated percolative, tunneling and total magnetoresistance. Comparing with the results in Fig.1, it is found that the simulated ones are consistent with experimental fact, which means that the spin-tunneling and percolative models are quite successful to explain magnetoresistance effect of CMR materials.

Fig.6 Simulated percolative, tunneling and total magnetoresistance as function of temperature
4 CONCLUSIONS
There are different magnetic field dependencies of magnetoresistance and magnetization in different temperature ranges, which means the existence of different magnetoresistance mechanism. Based on the models of spin-polarized tunneling and percolation, the simulated magnetoresistance character obtained using Monte Carlo method are consistent with experimental fact, which means that the spin-tunneling and percolative models are quite successful to explain the magnetoresistance effect of the manganese perovskite.
REFERENCES
[1]Tokura Y, Tomioka Y. Colossal magnetoresistive manganites [J]. J Magn Magn Mater, 1999, 200: 1-23.
[2]Coey J M D, Viret M, Molnar S V. Mixed-valence manganites [J]. Adv Phys, 1999, 48: 167-293.
[3]Gupta A, Gong G Q, XIAO G, et al. Grain-boundary effects on the magnetoresistance properties of perovskite manganite films [J]. Phys Rev B, 1996, 54: R15629-5633.
[4]JIANG Y, YUAN S L, HU J F, et al. Evidence of spin-polarized tunneling in phase-separated manganites La1/3Sr2/3-xBaxMnO3 [J]. Appl Phys Lett, 2001, 79: 3470-3473.
[5]Damay F, Cohen L F, Driscill J M, et al. Low-temperature grain boundaries effect in La0.7-xYxCa0.3-MnO3 [J]. J Magn Magn Mater, 2000, 214: L149-L154.
[6]Ziese M. Grain-boundary magnetoresistance in manganites: spin-polarized inelastic tunneling through a spin-glass-like barrier [J]. Phys Rev B, 1999, 60: R738-R741.
[7]Mahesh R, Mahendiran R, Raychaudhuri A K, et al. Effect of particle size on the giant magnetoresistance of La0.7Ca0.3MnO3 [J]. Appl Phys Lett, 1996, 68: 2291-2293.
[8]Chechersky V, Nath A, Isaac I, et al. Evidence for breakdown of ferromagnetic order below Tc in the manganite La0.8Ca0.2MnO3 [J]. Phys Rev B, 1999, 59: 497-502.
[9]Hart C, Hernandez A D, Ares O, et al. Extrinsic magnetoresistance in La2/3Ca1/3MnO3 thick films [J]. J Magn Magn Mater, 2001, 226-230: 905-907.
[10]Steinbeib E, Steenbeck K, Eick T, et al. Epitaxial thin films of magnetic perovskites-preparation, properties and possible applications [J]. Vacuum, 2000, 58: 135-148.
[11]Hwang H Y, Cheong S W, Ong N P, et al. Spin-polarized intergrain tunneling in La2/3Sr1/3MnO3 [J]. Phys Rev Lett, 1996, 77: 2041-2044.
[12]Zhang N, DING Wei-ping, ZHONG Wei, et al. Tunnel-type giant magnetoresistance in the granular perovskite La0.85Sr0.15MnO3 [J]. Phys Rev B, 1997, 56: 8138-8142.
[13]HUANG Zhi-gao, CHEN Zhi-gao, PENG Kun, et al. Monte Carlo simulation of tunneling magnetoresistance in nanostructured materials [J]. Phys Rev B, 2004, 69: 094420-1-094420-6.
[14]Bastiaansen P J M, Knops H J F. Percolation mechanism for colossal magnetoresistance [J]. Computational Materials Science, 1998, 10: 225-229.
[15]Kim H, Dho J, Lee S. Percolative phase separation induced by nonuniformly distributed excess oxygen in low-doped La1-xCaxMnO3+δ [J]. Phys Rev B, 2000, 62: 5674-5677.
[16]Ye S L, Song W H, Dai J M, et al. Large room-temperature magnetoresistance and phase separation in La1-xNaxMnO3 with 0.1≤x≤0.3 [J]. J Appl Phys, 2001, 90: 2943-2948.
[17]Yuan S L, Li Z Y, Peng G, Xiong C S, et al. Percolation model of the temperature dependence of resistance in doped manganese perovskites [J]. Appl Phys Lett, 2001, 79: 90-92.
[18]Millis A J, Littlewood P B, Shraiman B I. Double exchange alone does not explain the resistivity of La1-xSrxMnO3 [J]. Phys Rev Lett, 1995, 74: 5144-5147.
[19]Sheng L, Xing D Y, Sheng D N, et al. Metal-insulator transition in the mixed-valence manganites [J]. Phys Rev B, 1997, 56: R7053-7056.
[20]Furukawa N. Transport properties of the kondo lattice model in the limit S=∞ and D=∞ [J]. J Phys Soc Jpn , 1994, 63: 3214-3217.
[21]Yi H, Hong C S, Hur N H. Theoretical considerations on the transport property of La1-xCaxMnO3 in the paramagnetic regime [J]. Solid State Communications, 2000, 114: 579-583.
[22]Balcells LI, Fontcuberta I, Martinez B, et al. High-field magnetoresistance at interfaces in manganese perovskites [J]. Phys Rev B, 1998, 58: R14697-14700.
[23]Rivas J, Hueso L E, Fondado A, et al. Low field magnetoresistance effects in fine particles of La0.67-Ca0.33MnO3 perovskites [J]. J Magn Magn Mater, 2000, 221: 57-62.
[24]Markovich V, Rozenberg E, Yuzhelevski, Y et al. Correlation between electroresistance and magnetoresistance in La0.82Ca0.18MnO3 single crystal [J]. Appl Phys Lett , 2001, 78: 3499-3502.
[25]Coey J M D, Viret M, Ranno L, et al. Electron localization in mixed-valence manganites [J]. Phys Rev Lett, 1995, 75: 3910-3913.
[26]Tsai S H, Landau D P. Simulation of a classical spin system with competing superexchange and double-exchange interactions [J]. J Appl Phys, 2000, 87: 5807-5809.
Foundation item: Project(G1999064508) supported by the National Key Project for Basic Research of China; Project(E0320002) supported by NSF of Fujian Province of China
Received date: 2004-12-06; Accepted date: 2005-01-18
Correspondence: HUANG Zhi-gao, Professor, PhD; Tel: +86-591-83448993; E-mail: zghuang@fjnu.edu.cn


