J. Cent. South Univ. (2016) 23: 798-807
DOI: 10.1007/s11771-016-3126-9

Effect of copper slag recovery on hydrometallurgical cut-off grades considering environmental aspects
AFSHIN AKBARI1, ESMAEIL RAHIMI2
1. Department of Mining Engineering, Islamic Azad University-Central Tehran Branch, Tehran, Iran;
2. Department of Mining Engineering, Islamic Azad University-South Tehran Branch, Tehran, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract:
Determining the hydrometallurgical cut-off grades specifies the destination of low grade materials and this is subjected to more benefits in mining. Copper production rate is considered as one of the fundamental issues in hydrometallurgical cut-off grades determination. Slags are remarked as one of the main sources of copper. It is not only regarded as a waste but also identified as another resource extracting base metals. Slags are characterized by copper high grade. Thus, slag copper recovery can be led to different cut-off grades and net present value (NPV). The current research scrutinizes the effect of slag recovery by both flotation and hydrometallurgical methods on the hydrometallurgical cut-off grades. For this purpose, the optimum cut-off grade algorithms of hydrometallurgical methods are developed by considering associated environmental parameters, incomes and also the costs. Then, their optimum amounts are calculated with NPV maximization as an objective function. The results indicate that considering slag copper recovery in the hydrometallurgical cut-off grade algorithms reduces the environmental costs caused by slag dumping and leads to more NPV by 9%.
Key words:
1 Introduction
Since slags include specific mechanical properties, they are practiced as industrial materials in civil and road construction [1]. While copper slags are remarked as another important resource for extracting base metals [2], they are sometimes buried as waste materials. Slags are produced by different copper smelting processes [3]. The slags consist of electric (EF) and convertor furnaces (CF) with different chemical compositions in flash and reverbatory smelting processes [4]. The slags produced in direct blister methods include different mineralogy containing various oxide minerals as well as primary and secondary sulfides [5-6]. Hence, flotation [7], hydrometallurgical methods [8-11] and slags returning to the electric furnaces [12] are employed in Cu recovery from the slags due to their type of mineralogy. On the other hand, the slags cooling rate is very effective on their mineralogical and mechanical properties [13]. Copper recovery from slags not only reduces adverse environmental impacts of slag dumping [14] but also increases the benefits and production of copper. Thus, it is influential on the concentration and hydrometallurgical cut-off grades policy, so they must come into account in the calculation of optimum cut-off grades.
LANE [15] was the first who commenced to determine optimum cut-off grades. Later, he could represent an algorithm of optimum cut-off grades to optimize the NPV [16]. After LANE, many others attempted to calculate optimum cut-off grades with NPV maximization as an objective function [17-19]. In all these studies, optimum cut-off grades are figured out due to concentration method and the optimum cut-off grades of hydrometallurgical methods have not been determined. In 1979, DAVEY [20] tried to specify the optimum cut-off grades of hydrometallurgical methods. Therefore, he considered three material destinations indicated by leaching and concentration cut-off grades. He considered a fixed grade as the leaching cut-off grade at which it was not expected any copper recovery less than it. On the other hand, the concentration cut-off grade was obtained considering a relation between copper recovery through leaching and head grade of low grade ore. Although it was the first time that the leaching cut-off grades were calculated, it included some specific defects. Assuming a fixed grade, it could not lead to maximum NPV. On the contrary, using a head grade-recovery relation needs more leaching experiments, in regard to complexity of hydrometallurgical methods.
The utility functions of sending the materials to two destinations are applied by RENDU [21] to determine leaching and concentration cut-off grades. The opportunity cost was included in this approach [22]. This expenditure is also summarized in delay and change costs [23]. The presented method can lead to maximum amount of the NPV, however, the optimum leaching and concentration cut-off grades cannot be obtained simultaneously.
In 2013 and 2014, the effects of different processing methods on optimum cut-off grades are considered [24-25]. But they have not scrutinized the effect of copper recovery from process tailing on hydrometallurgical optimum cut-off grades. Moreover, the environmental consideration of these processing methods on optimum cut-off grades is not taken into account.
Since environmental parameters are very essential in mine production and optimum cut-off grades, many studies have been done in this regard [26-27]. KING [28] considered reclamation costs in mine design and RODRIGUEZ and ROZGONYI [29] declared that mine design can make more benefit just in case that the environmental parameters of mines are remarked. They also classified wastes from acid generating and non-acid generating points of view. RASHIDINEJAD et al [30] presented the algorithm of optimum cut-off grades based on RODRIGUEZ and ROZGONYI’s finding in 2008. Although all these studies have taken into account the effects of environmental parameters on concentration cut-off grades, they have ignored the influence of environmental parameters on hydrometallurgical cut-off grades. Then,environmental parameters of processing methods are considered in hydrometallurgical cut-off grade algorithms to solve these shortages [31]. However, it has not considered the influence of copper recovery from process tailing on the optimum cut-off grades.
The development of metallurgical science has been directed into extracting copper from slag that it is counted as one of the most important productions of smelting processes. High production capacity, high copper grade and their specific mineralogy of slag have made copper extraction both economically and environmentally significant [14]. The amount of final production is changed by extracting copper from its slags through hydrometallurgical and pyrometallurgical methods. Consequently, it changes the optimum cut-off grades of concentration and hydrometallurgical methods.
In this work, the algorithm of hydrometallurgical and concentration cut-off grades determination is first developed and then the effect of copper recovery from its slags on the optimum cut-off grades is evaluated. Moreover, environmental consideration of processing methods is analyzed in the presented model. Eventually, the hydrometallurgical optimum cut-off grades and maximum amount of NPV are calculated by an innovative optimization method and an iterative algorithm.
2 Methodology
2.1 Subject description
The determination of optimum hydrometallurgical cut-off grades aims at deciding the destination of low grade ores. In the previous algorithms, the determination of optimum cut-off grades can figure out the material destination to waste dumps or concentration plants. This is while, the new carried out algorithm determines the material destination to waste dumps, hydrometallurgical plants or flotation processes. Figure 1 describes the determination algorithm of material destination based on ore mineralogy and type of rocks.
In Fig. 1, the ore type is the basis of material destination. Hence, ore blocks identified as oxide ones are extracted by hydrometallurgical methods such as leaching (Scenario 1). Blocks are classified as the primary or secondary sulfide ones, and their appropriate method is chosen by the algorithm presented in this work from technical, economical and environmental view points.
This issue can be determined by second scenario of the flowchart. In the third scenario, there are blocks of ore in transition zones which can be sent to oxide and sulfide dumps through grade estimating. As observed in this flowchart, the amount of slag produced in smelter plants affects the ore destination as well as economical and environmental parameters. Obviously, the produced slag can be treated by hydrometallurgical and pyrometallurgical methods based on its mineralogy.
2.2 Effective parameters
2.2.1 Slag treatment
Recovering copper from slags is remarked as one of the factors affecting the cut-off grades of hydrometallurgical methods. These slags are treated by hydrometallurgical and pyrometallurgical methods according to their mineralogy. It is essential to calculate the tonnage of slag produced in smelter plants. It is also necessary to specify the average grade of slags to complete modeling. In fact, the rate of copper production from the slag  by two hydrometallurgical and pyrometallurgical methods can be determined by the following relation:
by two hydrometallurgical and pyrometallurgical methods can be determined by the following relation:
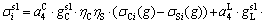
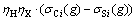 (1)
(1)
where i is the year indicator, 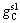 and
and  indicate the slag grades used in flotation and hydrometallurgical methods, respectively. σCi represents the annual materials sent to concentration plant, σS is the pyrometallurgical produced materials, ηC represents the concentration recovery and ηS indicates the recovery of smelter and electrorefining (ER) processes. ηH is the recovery of heap leaching and ηX introduces the solvent extraction (SX) and electrowining (EW) processes recoveries.
indicate the slag grades used in flotation and hydrometallurgical methods, respectively. σCi represents the annual materials sent to concentration plant, σS is the pyrometallurgical produced materials, ηC represents the concentration recovery and ηS indicates the recovery of smelter and electrorefining (ER) processes. ηH is the recovery of heap leaching and ηX introduces the solvent extraction (SX) and electrowining (EW) processes recoveries.  and
and  are respectively the amounts of slags treated by flotation and hydrometallurgical methods.
are respectively the amounts of slags treated by flotation and hydrometallurgical methods.

Fig. 1 Effects of copper slag treatment on material destination
In Eq. (1):
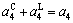 (2)
(2)
Also,
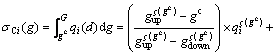
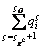 (3)
(3)
And
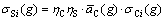 (4)
(4)
where  is equal to
is equal to
 (5)
(5)
where gc is the concentration cut-off grades, G represents the maximum grade, qi is the annual tonnage of materials,  is the grade category indicator, gup and gdown are the upper and lower limits of the grade category in the grade distribution table, respectively, and
is the grade category indicator, gup and gdown are the upper and lower limits of the grade category in the grade distribution table, respectively, and 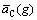 indicates the average grade of material sent to concentration plants.
indicates the average grade of material sent to concentration plants.
2.2.2 Environmental parameters
Both hydrometallurgical and pyrometallurgical methods can make different environmental pollution [32]. It is economically essential to identify environmental parameters of different processing methods because they can affect the profitability of processes. If the cut-off grade policy is to achieve economic purposes, it is necessary to consider the environmental aspects of processing methods in optimum cut-off grade algorithms. Figure 2 illustrates the environmental parameters of hydrometallurgical and pyrometallurgical methods.
The parameters introduced in Fig. 2 are considered in the algorithm of optimum cut-off grades. Consequently, the environmental costs of processing methods are calculated in different steps of processes. The costs analysis and cut-off grades algorithms reveal that there is an interactive relationship between the environmental parameters and cut-off grade policy. It means a balance and any change on them affects another.

Fig. 2 Schematic diagram of copper production and processes (Amount of leached material remained on heap (a1/ %); amount of SX and EW tailing (a2/%); amount of concentration tailing (a3/%); amount of smelter and ER tailing (a4/%))
2.2.3 Controlling capacities
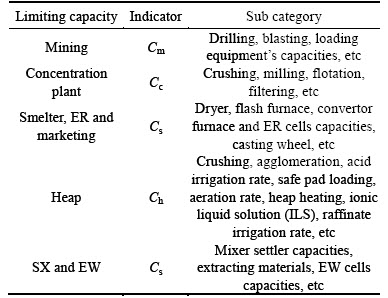
The limitation of mine and plants capacities leads to opportunity costs and this is contemplated as an important cost in the calculation of hydrometallurgical optimum cut-off grades. On the other hand, the production life is restricted by mine and plants capacities. Such limitations usually embrace some other sub-limitation affecting the production life. These limitations and sub-limitations are defined in Table 1.
Table 1 Limiting capacities and sub-limitation
2.2.4 Price, costs and recoveries
The most essential factors affecting the hydrometallurgical optimum cut-off grades are copper price and incomes which are noted in the algorithm of optimum cut-off grades determination. Operating costs are also effective in determining ore destination. Cost related to the solvents is considered as the main operating cost of hydrometallurgical methods. Thus, this cost is remarked as another parameter influencing the hydrometallurgical optimum cut-off grades. The costs of electrical energy and fuel are counted as parameters affecting the economy of pyrometallurgical processes. On the other hand, optimum cut-off grades are the function of processing recoveries. Two types of recovery are defined in pyrometallurgical processes. One recovery is related to flotation method and the other to smelting method. Only one recovery is described due to the nature of hydrometallurgical methods particularly heap leaching one and it is related to heap. Holistically, in SX process and EW, the amount of the lost copper is negligible and it is operated in a closed cycle. As a matter of fact, processing recovery is not defined for such plants.
2.3 Objective function
The objective function of the hydrometallurgical optimum cut-off grades determination is to maximize the NPV. Time value of money (TVM) and annual cash flows are subjected to specify the NPV. From another point of view, the calculation of the material sent to hydrometallurgical and concentration processes affects the determination of annual cash flows and it is also necessary to specify optimum cut-off grades. Figure 3 indicates the calculation method of optimum cut-off grades by determining the amount of material sent to processing plants.
As observed in Fig. 3, the determination of optimum cut-off grades is a function of ore tonnage sent to plants and the curve of grade-tonnages distribution. Hence, the ore tonnage sent to heap (σHi) is calculated by Eq. (6) in the continuous and discounted grade distribution forms:
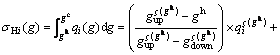
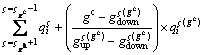 (6)
(6)
where gh introduces hydrometallurgical cut-off grades.

Fig. 3 Effect of mined material tonnage on cut-off grades
As mentioned earlier, the amount of ore sent to concentration plants in two forms is calculated by Eq. (3).
Calculating the amount of final production by hydrometallurgical method (σXi) is regarded as other important parameters in specifying the annual cash flow that is determined as continuous and discounted forms through Eqs. (7) and (8). Moreover, the amount of produced copper by pyrometallurgical method is calculated by Eq. (4).
 (7)
(7)
or
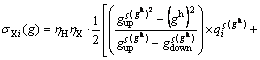
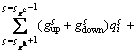
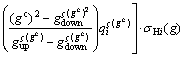 (8)
(8)
where  represents the average grade of material sent to hydrometallurgical plants. In Eqs. (3), (4), (6) and (7),
represents the average grade of material sent to hydrometallurgical plants. In Eqs. (3), (4), (6) and (7),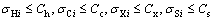
Equation (9) is able to specify the amount of the annual cash flows considering copper recovery from slags and environmental parameters.
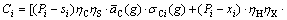
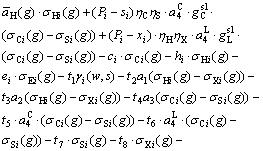
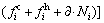 (9)
(9)
where P is the commodity price and s represents the smelting production costs. f c is the fixed cost of pyrometallurgical processes and f h indicates the fixed cost of hydrometallurgical processes. xi can be categorized to the annual operating costs of SX (xSXi) and EW (xEWi) plants. Ci, hi and ei are the operating costs of concentration and hydrometallurgical processes and mine, respectively. Also, σEi indicates the total mined material and γi(w, s) introduces the waste material which can be sent to stockpiles or waste dumps.  is the discount rate.
is the discount rate.
In Eq. (9), there is the opportunity cost. Since there is limitation in mine and plants capacities, the opportunity cost is inevitable. In the presented model, there are five limits. The opportunity cost is shown as  ·Ni in Eq. (9) and it has a direct connection with the NPV during mine life. As the NPV is reduced in mine life, this cost is also decreased. Furthermore, the amount of NPV is calculated in continuous and discounted forms of grade distribution by substituting the annual cash flows in Eq. (10):
·Ni in Eq. (9) and it has a direct connection with the NPV during mine life. As the NPV is reduced in mine life, this cost is also decreased. Furthermore, the amount of NPV is calculated in continuous and discounted forms of grade distribution by substituting the annual cash flows in Eq. (10):
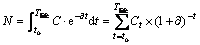 (10)
(10)
where to is the time of project beginning, and Tlife is the project life.
3 Results and discussion
3.1 Limiting and balancing cut-off grades
The optimum cut-off grades are calculated through considering various restrictions and solving Lagrangian equation sets. In fact, the optimum cut-off grades of hydrometallurgical methods are specified by relations presented in supplementary file as ESM-1.
In ESM-1 relations, 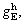
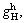
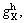
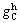 and
and 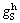 are respectively the optimum cut-off grades of hydrometallurgical methods considering the mine, heap loading, SX and EW, concentration, smelter and refinery capacity limitation. The optimum cut-off grades of concentration methods are also determined by relations indicated in supplementary file as ESM-2.
are respectively the optimum cut-off grades of hydrometallurgical methods considering the mine, heap loading, SX and EW, concentration, smelter and refinery capacity limitation. The optimum cut-off grades of concentration methods are also determined by relations indicated in supplementary file as ESM-2.
In ESM-2 relations, 

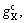
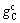 and
and 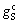 are respectively the optimum cut-off grades of concentration methods considering the five defined restrictions.
are respectively the optimum cut-off grades of concentration methods considering the five defined restrictions.
The ESM-1 and ESM-2 calculated grades are called limiting cut-off grades. In the case that the capacity of two operations simultaneously limits the production capacity, 10 dual balancing cut-off grades are calculated due to 5 limiting capacities. On the other hand, three capacities might simultaneously limit the capacity of final production. In this case, 10 balancing cut-off grades are specified called triple balancing cut-off grades. The limitations defined in Lagrange equations are expressed by following ratios to calculate dual balancing cut-off grades:
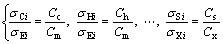 (11)
(11)
Furthermore, the triple balancing cut-off grades are calculated by limits in Lagrange equation as follows:
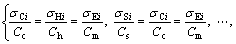
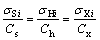 (12)
(12)
An iterative algorithm is needed to calculate the maximum amount of NPV because there is an unknown NPV in Eq. (9). This algorithm should be able not only to find out the maximum amount of NPV, but also to calculate the maximum amounts of the unknown ones (the optimum cut-off grades of processing methods). As the mathematical calculations of optimum cut-off grades and performing the iterative algorithm are complicated enough, it is developed by mathematic software and MATLAB programming. The innovative optimization algorithm is presented in Fig. 4.
As observed in the algorithm, it is required to assume an initial cut-off grade. The best amount of this initial assumption is the optimum, limiting, dual or triple balancing cut-off grades resulting to the maximum NPV. After calculating the limiting and balancing cut-off grades by multivariable optimization method, the amount of the initial assumption can be determined by mathematical operation. The geometrical depiction of optimum, balancing and limiting grades can contribute to a better realization of this optimization algorithm. As it is geometrically depicted in Fig. 5, the limiting cut-off grades are the maximum surface of annual cash flows. Dual balancing cut-off grades are geometrically considered as the maximum of two cash flow surfaces intersecting curves. Triple balancing cut-off grades locate on three cash flow surfaces intersection point. Eventually, the first assumption of optimum cut-off grades is geometrically found in the surface maximum, passing through the minimum of all cash flow surfaces.
3.2 Case study
Miduk deposit is a porphyry copper mine divided into 3 zones including oxide, Supergene and Hypogene. The primary and secondary ore body is estimated as 170 Mt copper ores by average grade of 0.44% with 144 Mt minable reserves. The grade distribution of Miduk deposit is as shown in Table 2.
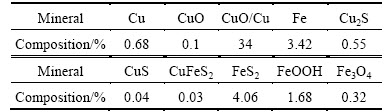
The chemical composition of much of this deposit is summarized in Table 3.
Table 3 illustrates the Miduk reserve predominantly composed of supergene copper minerals. Therefore, the deposit can be processed by pyrometallurgical and hydrometallurgical methods.
The concentrate produced by Miduk concentration plant is sent to Khatoon Abad smelting plant. This plant already works with reverbatory furnace that improves its process to flash method. The chemical composition and mineralogical analyses of a sample from these slags are presented in SM-3.
The experiments preformed in this regard indicate the success of flotation process in processing EF slags. Such success requires providing slow cooling rate by slag ditch or ladle. Remarkably, the fast cooled slags of CF are treated by hydrometallurgical methods. According to the above items and the possibility of recovering copper from the Miduk slags, the hydrometallurgical optimum cut-off grades can be calculated. The amounts of both economical and environmental parameters are displayed in Table 4, to calculate the optimum cut-off grades of Miduk copper mine.

Fig. 4 Innovative algorithm to calculate maximum NPV and optimum hydrometallurgical cut-off grades

Fig. 5 Illustrative figure of optimum, limiting (LG), dual (DBG) and triple (TBG) balancing cut-off grades of Miduk mine
Table 2 Grade-tonnage distribution of Miduk copper mine

Table 3 Chemical composition of a sample of Miduk copper mine
The optimum cut-off grades of concentration and hydrometallurgical methods are calculated by the innovated algorithm as shown in Table 5. Moreover, the maximum amount of cash flows and NPV considering the copper recovery from the slags are illustrated in these tables.
In other case, it is assumed that the copper of slags is not recovered. Thus, concentration and hydrometallurgical optimum cut-off grades are presented as Table 6.
Comparing Tables 5 and 6 proves that recovering the copper from slags lead to decreasing the optimum cut-off grades of concentration and hydrometallurgical methods. It is also observed that more annual cash flows are obtained considering the slag treatment.
Table 4 Costs, limiting capacities and process recoveries of Miduk mine
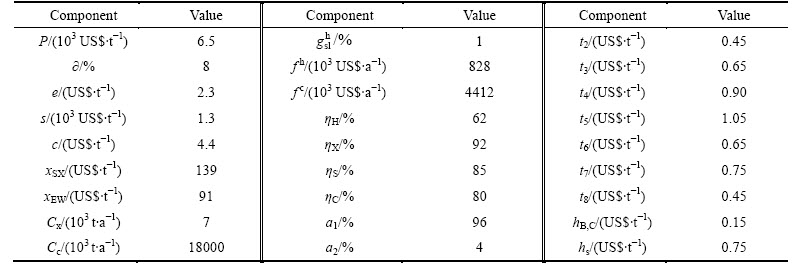
Table 5 Optimum concentration and hydrometallurgical cut-off grades policy of Miduk mine with copper slag treatment

Table 6 Optimum concentration and hydrometallurgical cut-off grades policy of Miduk mine without copper slag treatment
Figure 6 compares the environmental costs and NPV of these two conditions with each other.
As observed in Fig. 6, the unit environmental costs get less in which copper is recovered from slags. It is also demonstrated that copper slag treatment of Miduk mine leads to more NPV by 19%.

Fig. 6 Variations of NPV and environmental cost unit during operation life
4 Conclusions
Although hydrometallurgical methods are being developed in copper industry, their effects on optimum cut-off grades are usually ignored. The current research assesses the effect of copper recovery from slags using flotation and hydrometallurgical methods on the hydrometallurgical and concentration optimum cut-off grades. The results of this research demonstrate the below items:
1) Copper recovery from slag not only increases the NPV in mines but also reduces the unit environmental costs of copper production. This reduction of environmental costs is because many expenses related to dump, disposal or neutralizing slags by its processing are removed.
2) The optimum cut-off grades are decreased through processing copper from slags and this problem changes the low grade ore destination.
3) The optimization algorithm indicates that the optimum cut-off grades follow decreasing policy during mine life regarding copper recovery from slag. This policy is also observed in the unit environmental costs of processing methods.
Acknowledgements
The authors are grateful to Canymes Company as the general contractor of Khatoon Abad smelter and Miduk leaching plants for providing EF and CF slag samples and related information. Also, we gratefully thank the University Language Center, especially Mrs. Azarme, for her cooperation in reviewing and editing this paper.
References
[1] LAVANYA C, SREERAMA RAO A, DARGA KUMAR N. A review on utilization of copper slag in geotechnical applications [C]// Proceedings of Indian Geotechnical Conference. New Delhi, India, 2011: H-212.
[2] PALACIOS J,  M. Wastes as resources: Update on recovery of valuable metals from copper slags [J]. Mineral Processing and Extractive Metallurgy, 2011, 120(4): 218-223.
M. Wastes as resources: Update on recovery of valuable metals from copper slags [J]. Mineral Processing and Extractive Metallurgy, 2011, 120(4): 218-223.
[3] SCHLESINGER M, KING M, SOLE K C, DAVENPORT W G. Extractive metallurgy of copper [M]. Fifth edition. Oxford (UK): Elsevier Science Ltd. 2011: 88-89.
[4] MURARI K,SIDDIQUE R,JAIN K. Use of waste copper slag, a sustainable material [J]. Journal of Material Cycles and Waste Management, 2015, 17(1): 13-26.
[5] MAKINEN J K, JAFS G A. Production of matte, white metal, and blister copper by flash furnace [J]. JOM, 2013, 34(6): 54 -59.
[6]  K, KUCHARSKI M. The rate of metal oxygen reduction from the slag of the direct-to-blister flash smelting process [J]. Archives of Metallurgy and Materials, 2010, 55(1): 317-323.
K, KUCHARSKI M. The rate of metal oxygen reduction from the slag of the direct-to-blister flash smelting process [J]. Archives of Metallurgy and Materials, 2010, 55(1): 317-323.
[7] HUANG H, ZHU H, HU Y. Hydrophobic-surface of copper from converter slag in the flotation system [J]. International Journal of Mining Science and Technology, 2013, 23(4): 613-617.
[8] CARRANZA F, ROMERO R, MAZUELOS A, IGLESIAS N, FORCAT O. Biorecovery of copper from converter slags: Slags characterization and exploratory ferric leaching tests [J]. Hydrometallurgy, 2009, 97: 39-45.
[9] YANG Z, RUI-LIN M, WANG-DONG N, HUI W. Selective leaching of base metals from copper smelter slag [J]. Hydrometallurgy, 2010, 103: 25-29.
[10] CHEN M S H, HAN Z R, WANG L Z. Recovery of valuable metals from copper slag by hydrometallurgy [J]. Advanced Materials Research, 2011, 402: 35-40.
[11] NADIROV R K, SYZDYKOVA L, ZHUSSUPOVA A, USSERBAEV M. Recovery of value metals from copper smelter slag by ammonium chloride treatment [J]. International Journal of Mineral Processing, 2013, 124: 145-149.
[12] COURSOL P, VALENCIA N,MACKEY P, BELL S, DAVIS B. Minimization of copper losses in copper smelting slag during electric furnace treatment [J]. Journal of Mining, Material and Metallurgy, 2012, 64(11): 1305-1313.
[13] TSHIONGO N, MBAYA R K, MAWEJA K, TSHABALALA L. Effect of cooling rate on base metals recovery from copper matte smelting slags [J]. World Academy of Science, Engineering and Technology, 2010, 70: 273-277.
[14]  M, SUDBURY M. Physicochemical characterization of copper slag and alternatives of friendly environmental management [J]. Journal of Mining and Metallurgy B: Metallurgy, 2013, 49(2): 161-168.
M, SUDBURY M. Physicochemical characterization of copper slag and alternatives of friendly environmental management [J]. Journal of Mining and Metallurgy B: Metallurgy, 2013, 49(2): 161-168.
[15] LANE K F. Choosing the optimum cut-off grades [J]. Colorado School Mines, 1964, Q59: 485-492.
[16] LANE K F. The economic definition of ore-cut-off grades in theory and practice [M]. California: Mining Journal Books Limited, 1988: 77-81.
[17] BASCETIN A, NIETO A. Determination of optimal cut-off grade policy to optimize NPV using a new approach with optimization factor [J]. The Journal of the Southern African Institute of Mining and Metallurgy, 2007, 107: 87-94.
[18] DAGDELEN K, KAZUHIRO K. Cutoff grade optimization for large scale multi-mine, multi-process mining operations, mine planning and equipment selection [C]// International Symposium. Bangkok: Curran Associates, 2007: 226-233.
[19] ASAD M W A, TOPAL E. Net present value maximization model for optimum cut-off grade policy of open pit mining operations [J]. The Journal of the Southern African Institute of Mining and Metallurgy, 2011, 111: 741-750.
[20] DAVEY R. Mineral block evaluation criteria [M]// HUSTRULID W, KUCHTA M. Open pit mine planning and design. Roiterdam, Netherlands: SME-AIME, 1979: 83-96.
[21] RENDU J M. An introduction to cutoff grade estimation [R]. The Society for Mining, Metallurgy and Exploration Inc. 2008.
[22] RENDU J M. Cut-off grade estimation – old principles revisited – application to optimisation of net present value and internal rate of return [R]. Orebody Modelling and Strategic Mine Planning. Perth, 2009: 165-169.
[23] WHITTLE J, WHARTON C. Optimizing cut-off grades [J]. Mining Magazine, 1995, 1(1): 287–289.
[24] ASAD M, DIMITRAKOPOULOS R. A heuristic approach to stochastic cutoff grade optimization for open pit mining complexes with multiple processing streams [J]. Resources Policy, 2013, 38(4): 591-597.
[25] RAHIMI E, ORAEE K, SHAFAHI Z, GHASEMZADEH H. Determining the optimum cut-off grades in sulfide copper deposits [J]. Archives of Mining Scince, 2014, 60(1): 313-328.
[26] OSANLOO M, RASHIDINEJAD F, REZAI B. Incorporating environmental issues into optimum cut-off grades modeling at porphyry copper deposits [J]. Resources Policy, 2008, 33(4): 222–229.
[27] RAHIMI E, GHASEMZADEH H. A new algorithm to determine optimum cut-off grades considering technical, economical, environmental and social aspects [J]. Resource Policy, Doi:10.1016/j.resourpol.2015.06.004.
[28] KING B M. Impact of rehabilitation and closure costs on production rate and cutoff grade [C]// International Symposium. London: United Kingdom Royal School of Mines, APCOM: 8-9.
[29] RODRIGUEZ R, ROZGONYI T G. Evaluating the impact of environmental considerations in open pit mine design and planning [C]// International Symposium on Environmental Issues and Waste Management in Energy and Mineral Production. Antalya, Turkey: SWEMP, 2004: 125-131.
[30] RASHIDINEJAD F, OSANLOO M, REZAI B. Cutoff grades optimization with environmental management; A case study: Sungun copper project [J]. IUST International Journal of Engineering Science, 2008, 19: 1-13.
[31] RAHIMI E, ORAEE K, SHAFAHI Z, GHASEMZADEH H. Considering environmental costs of copper production in cut-off grades optimization [J]. Arab Journal of Geoscince, Doi: 10.1007/s12517-014-1646-x.
[32] GUPTA CH K. Chemical metallurgy: Principles and practice [M]. Mumbai: Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. 2006: 33-36, 112-116.
(Edited by YANG Bing)
Received date: 2015-03-25; Accepted date: 2015-07-27
Corresponding author: ESMAEIL RAHIMI, PhD; Tel: +98-2184335430, +98-9124590976; E-mail: Se_rahimi@azad.ac.ir, S.rahimi3163@gmail.com
Abstract: Determining the hydrometallurgical cut-off grades specifies the destination of low grade materials and this is subjected to more benefits in mining. Copper production rate is considered as one of the fundamental issues in hydrometallurgical cut-off grades determination. Slags are remarked as one of the main sources of copper. It is not only regarded as a waste but also identified as another resource extracting base metals. Slags are characterized by copper high grade. Thus, slag copper recovery can be led to different cut-off grades and net present value (NPV). The current research scrutinizes the effect of slag recovery by both flotation and hydrometallurgical methods on the hydrometallurgical cut-off grades. For this purpose, the optimum cut-off grade algorithms of hydrometallurgical methods are developed by considering associated environmental parameters, incomes and also the costs. Then, their optimum amounts are calculated with NPV maximization as an objective function. The results indicate that considering slag copper recovery in the hydrometallurgical cut-off grade algorithms reduces the environmental costs caused by slag dumping and leads to more NPV by 9%.


