
3D finite element method analysis of deformation and temperature rise during equal-channel angular pressing
ZHANG Xin-ping(张新平), CHEN Guang(陈 光), WANG Xue(汪 雪),
LING Jie(林 杰), WU Mei(吴 媚)
Department of Materials Science and Engineering, Nanjing University of Science and Technology,
Nanjing 210094, China
Received 20 April 2006; accepted 30 June 2006
Abstract:
The material flow, temperature rise of the billet and pressing load during equal-channel angular process (ECAP) were studied by using 3D finite element method for Cu at different corner angle of mold, interfacial friction coefficient between the billet and the mold. As corner angle increases, the magnitude of shear deformation decreases and the strain difference between upper and lower part of the material becomes more apparent. The pressing load and peak temperature rise of the billet become low as the interfacial friction coefficient decreases. The effects of the corner angle of mold on the temperature rise of the billet can be ignored, but the effects of the friction coefficient between the mold and the billet must be taken into account. For pressing load, the effect of the friction coefficient is larger than that of the corner angle. A good agreement between the simulated and measured material flow is obtained.
Key words:
finite element method; equal-channel angular pressing; material flow; pressing load; temperature distribution;
1 Introduction
Equal-channel angular pressing (ECAP) is a metal processing technique, developed by SEGAL over two decades ago [1]. It is an attractive grain-refining method to obtain bulk nanostructured materials in which grain sizes are up to about 100 nm. During ECAP, the billet undergoes severe plastic deformation as it passes through the intersection of the two channels of equal cross-sectional area with a predetermined angle. Since there is no change in area, this process can be repeated to impose large cumulative strains in the materials [2-8].
In recent years, many original and review papers have been devoted to this technique, connected with the features of ultrafine-grained structure and the development of properties during ECAP [1-10]. To understand the material behavior under ECAP, various researches were performed by computer simulation technique. LIU et al [11, 12] analysed the load of ECAP, and they proposed a new shape die, which decreases the tensile stress based on FEM results. BOWEN et al [13] studied the effects of the tooling configuration, friction coefficient conditions and back pressure on the deformation behaviour in ECAP by both finite element analysis and experiments. A computer simulation of ECAP by using DEFORM-2D software was performed to understand stress, strain variation during ECAP, die gap corner formation which is affected by material strain hardening rate in ECAP, and mold geometry effect during ECAP[14-16]. JON et al [17] studied the pressures needed for non-friction coefficient equal-channel angular pressing (ECAP) of perfectly plastic or strain-hardening materials by using analytical approximations (upper-bound type) and numerical (finite-elements) methods. PRANGNELL et al [18] presented a simplified finite element model, which had been used to investigate ECAP process. However, the isothermal condition was assumed in those studies. DONG et al [19, 20] studied the effect of pressing temperature on microstructure and tensile behavior of low carbon steels and Ti processed by equal channel angular pressing, and it was shown that ECAP temperature has an important effect on the microstructure and properties of materials processed by equal channel angular pressing. Although DUTTON et al [21] made nonisothermal simulations, the temperature rise in the billet due to deformation heating was not analyzed in their work. PEI et al [22] investigated the temperature rise and temperature distribution in the billet during equal channel angular pressing by using the finite element method for Al-1%Mg and Al-3%Mg at different pressing speeds.
The temperature rise of the billet will change the recrystallization temperature and thus affect the grain size formed [8, 9]. It is therefore necessary to analyze the deformation heating and the temperature rise during ECAP for precise control of the recrystallization temperature, and hence of the grain size.
In additional, most of above FEM researches are 2D results, and there is few report on 3D results. In this study, strain values for four kinds of the geometry of the mold were analysed by 3D FEM, and the results were compared with those of the actual deformation. 3D finite element method was used to study the material flow, pressing load and temperature rise in the billet during ECAP process. The effects of the corner angle and the friction coefficient on the temperature rise of the billet and the pressing load were also investigated.
2 Experiment and analysis
2.1 Deformation analysis
For the detailed analysis of the billet deformation, experimental strain measurement was performed to get the actual plastic strain values. Two pieces of rectangular billets having 80 mm in length, 12 mm in width and 6 mm in thickness were prepared and polished finally with 1 μm diamond paste. The polished surfaces were mecha- niccally engraved with square grids with the size of 2 mm×2 mm and faced together to avoid the erosion by wear between inner walls of the ECAP mold and the grid engraved surface of split billets. The ECAP molds with a channel angle φ= 90? between the entrance and exit channels and corner angle ψ=0?, 22?, 60?, 90? were employed for this experiment, as shown in Fig.1. The plunger load was measured. The ECAP was done only for the grid engraved pure copper billets at room temperature with a constant plunger speed of 1 mm/s, and the 10 mm long billet was left unextruded for the observation of grid distortion.
2.2 Finite element analysis of ECAP process
Finite element simulation of the ECAP process was carried out using the metal forming code DEFORM 3D. 3D plane strain and heat transfer models were used. The mold and plunger were assumed as rigid body. The billet material used in the calculations was annealed pure copper. Because the stress–strain curve of the high strain range, which is necessary for the FEM calculation of the SPD processes, cannot be obtained by conventional experimental techniques, the flow curve of the pure Cu was calculated up to large strain of 6 using the dislocation cell evolution model [16], as shown in Fig.2, which can describe the hardening behaviour of cell-forming crystalline materials at large strains. In all simulations, automatic remeshing was used to accommodate large strains and the occurrence of flow localization, which prevents further calculation during the simulation.
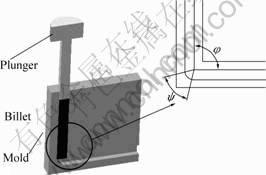
Fig.1 Schematic diagram of billet and ECAP mold
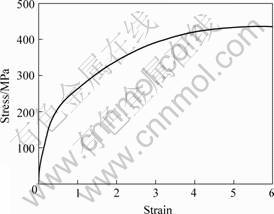
Fig.2 Stress—strain curve for annealed pure Cu used in FEM simulation
The mechanical and thermal constants of pure Cu [13] are shown in Table 1.
3 Results
3.1 Deforming processing of ECAP
A type deforming processing of Cu during ECAP is shown in Fig.3. It is clear that the strain of the part of the billet along inner angle of the mold is the maximum and accordingly the stress and temperature rise of that is the maximum, as shown in Fig.4 and Fig.5. From Fig.4, it can be seen that the stress distribution is very complicated, there being not only compressive stress but also tensile stress in the billet, the tensile stress being located around the corner of the mold.
Table 1 Mechanical and thermal constants of pure Cu used in FEM[13]

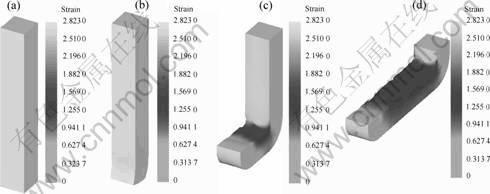
Fig.3 Strain distributions of billet during ECAP process for different time: (a) 0; (b) 60 s; (c) 270 s; (d) 600 s
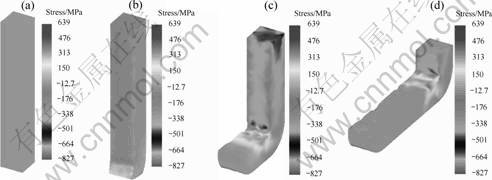
Fig.4 Stress distributions of billet during ECAP process for different time: (a) 0; (b) 60 s; (c) 270 s; (d) 600 s

Fig.5 Temperature distributions of billet during ECAP process for different time: (a) 0; (b) 60 s; (c) 270 s; (d) 600 s
3.2 Effect of ψ on ECAP process
Fig.6 shows the deformation patterns of the billets calculated and those of experiment at different shape parameters of ψ with fixed φ= 90?. The calculated results are very close to those of experiment. The grid distortion directly indicates the magnitude of shear deformation. Figs.6(a) and (a′) show uniform shear deformation over the whole material in the case of ψ=0?. In Fig.6(b) and (b′) simulated in ψ=22?, sheared lattice can hardly be seen in the lower part, which causes non-uniform shear deformation. As the angle ψ increases, the magnitude of shear deformation decreases and the strain difference between upper and lower part of the material becomes more apparent. It indicates that the bigger the angle ψ, the more severe the magnitude of the inhomogeneity.
The pressing loads calculated and measured at different shape parameters of ψ with fixed φ= 90? are shown in Fig.7. It is clear that the calculated results are in agreement with those of measured ones.
Fig.8 shows the effects of ψ on peak temperature rise of the billet during ECAP process. As the angle ψ increases, the value of the peak temperature rise of the billet decreases. But the temperature rise is very little.
3.3 Effect of interfacial friction coefficient on ECAP process
The effects of interfacial friction coefficient between the billet and the mold on pressing load and peak temperature rise of the billet during ECAP process are shown in Fig.9 and Fig.10. It is evident that the pressing load and peak temperature rise of the billet become low as the interfacial friction coefficient decreases. This means that as the interfacial friction coefficient decreases, the passage of the material through the die becomes easier. In the case of friction coefficient of 0.4, the temperature rise is about 40 ℃.
4 Discussion
The deformation behavior of ECA pressing was investigated with a fixed channel angle (φ) of 90? and ψ angles of 0?, 22?, 60? and 90?. It should be noted from Fig.7 that 3 stages of the ECAP load can be distinguished in this particular case. During the stage I, the load increases fast, and the front part of the billet goes through the main deformation zone in which most of the deformation occurs, see Figs.3(a) and (b). During stage Ⅰ, the volume of the deformation part of the billet increases, as does the internal stress within the billet, and the load increases fast, as well as the initially undeformed billet goes through the main deformation zone. Stage Ⅱ is the step where the front part of the billet exits the main deformation zone and bends to the upper side in the exit channel, see Figs.3(b) and (c). Since the front part of the billet passing the main deformation zone has no severe constraint for deformation until it touches the upper side of the exit channel die during bending, the load is a constant. The bent front part of the billet does not entirely fill the exit channel and a narrow gap between the billet and corner
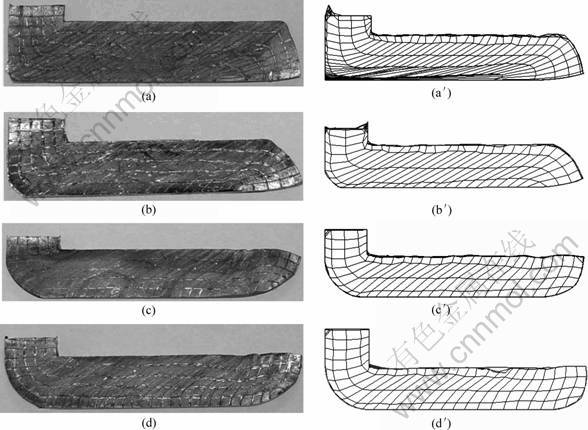
Fig.6 Material flow of Cu during ECAP process with varying corner angle, the left is experimental result and the right is analytical one: (a), (a′) ψ=0?; (b), (b′) ψ=22?; (c), (c′) ψ=60?; (d), (d′) ψ=90?
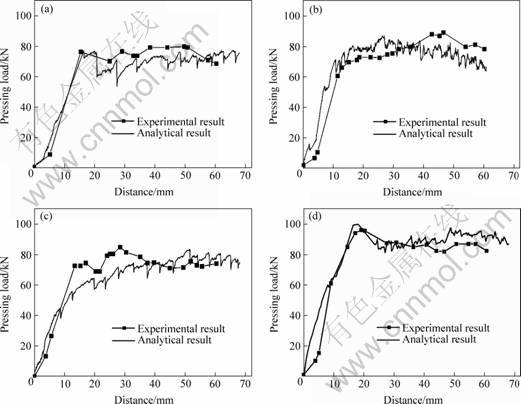
Fig.7 Pressing load during ECAP process with varying corner angle: (a) ψ=0?; (b) ψ=22?; (c) ψ=60?; (d) ψ=90?

Fig.8 Effects of ψ on peak temperature rise of billet during ECAP process

Fig.9 Effects of interfacial friction coefficient on pressing load during ECAP process
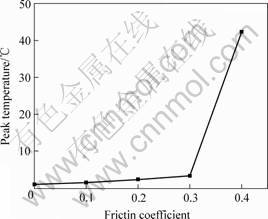
Fig.10 Effects of interfacial friction coefficient on peak temperature rise of billet during ECAP process
region of the exit channel die is generated. For the final stage Ⅲ, the end part of the billet goes out of the main deformation zone and the load drops precipitously.
There are some difference between the calculated results of pressing loads and those of the actual deformation, as shown in Fig.7. It may be that the friction coefficient between the billet and the mold is fixed in the case of FEM calculating, and the friction coefficient varies during experimental process. There are many reasons for the friction coefficient variations during the experimental process. For example, the oil film between the billet and the mold may be destroyed, or the surface roughness is not changeless for every region of the mold and the billet.
The effects of the corner angle ψ of mold on the temperature rise of the billet, as shown in Fig.8, can be ignored. But the effects of the friction coefficient between the mold and the billet must be taken into account, as shown in Fig.10. For pressing load, the effect of the friction coefficient is larger than that of the corner angle ψ.
5 Conclusions
1) 3D finite element method was used to study the material flow, pressing load and temperature rise in the billet during ECAP process. A good agreement between the simulated and measured material flow is obtained.
2) The simulation results show that the effects of the corner angle ψ of mold on the temperature rise of the billet can be ignored. But the effects of the friction coefficient between the mold and the billet must be taken into account. For pressing load, the effect of the friction coefficient is larger than that of the corner angle ψ.
References[1] MUGHRABI H, HEPPEL H W, KAUTZ M. Fatigue and microstructure of ultrafine-grained metals produced by severe plastic deformation[J]. Scripta Mater, 2004, 51: 807-812.
[2] IWAHASHI Y, HORITA Z, NEMOTO M, et al. The process of grain refinement in equal-channel angular pressing [J]. Acta Materialia, 1998, 46: 3317-3331.
[3] CHANG S Y, LEEB K S, CHOIC S H, et al. Effect of ECAP on microstructure and mechanical properties of a commercial 6061 Al alloy produced by powder metallurgy[J]. Journal of Alloys and Compounds, 2003, 354: 216-220.
[4] SKRIPNYUK V M, RABKIN E, ESTRIN Y, et al. The effect of ball milling and equal channel angular pressing on the hydrogen absorption/desorption properties of Mg-4.95 wt% Zn-0.71 wt% Zr (ZK60) alloy [J]. Acta Materialia, 2004, 52: 405-414.
[5] SEMENOVA I P, RAAB G I, SAITOVA L R, et al. The effect of equal-channel angular pressing on the structure and mechanical behavior of Ti-6Al-4V alloy [J]. Mater Sci Eng A, 2004, 387-389: 805-808.
[6] STOLYAROV V V, LAPOVOK R, BRODOVA I G, et al. Fine-grained Al-5wt.%Fe alloy processed by ECAP with back- pressure[J]. Mater Sci Eng A, 2003, 357: 159-167.
[7] XU C, FURUKAWA M, HORITA Z, et al. Severe plastic deformation as a processing tool for developing superplastic metals[J]. Journal of Alloys and Compounds, 2004, 378: 27-34.
[8] WANG Y M, MA E. Three strategies to achieve uniform tensile deformation in a nanostructured metal [J]. Acta Materialia, 2004, 52: 1699-1709.
[9] PARK K T, KIM Y S, LEE J G, et al. Thermal stability and mechanical properties of ultrafine grained low carbon steel[J] . Mater Sci Eng A, 2000, 293: 165-172.
[10] MOON B S, KIM H S, HONG S I. Plastic flow and deformation homogeneity of 6061 Al during equal channel angular pressing [J]. Scripta Mater, 2002, 46: 131-136.
[11] LIU Z Y, WANG Z J. Finite-element analysis of the load of equal-cross-section lateral extrusion [J]. J Mater Proc Technol, 1999, 94:193-196.
[12] LIU Z Y, LIU G, WANG Z R. Finite element simulation of a new deformation type occurring in changing-channel extrusion[J]. J Mater Proc Technol, 2000, 102: 30-32.
[13] BOWEN J R, GHOLINIA A, ROBERTS S M, et al. Analysis of the billet deformation behaviour in equal channel angular extrusion[J]. Mater Sci Eng A, 2000, 287: 87-99.
[14] HYOUNG S K, MIN H S, SUN I H. Plastic deformation analysis of metals during equal channel angular pressing [J]. J Mater Proc Technol, 2002, 113: 622-626.
[15] HYOUNG S K, MIN H S, SUN I H. Finite element analysis of equal channel angular pressing of strain rate sensitive metals[J]. J Mater Proc Technol, 2002, 130-131: 497-503.
[16] HYOUNG S K. Finite element analysis of deformation behaviour of metals during equal channel multi-angular pressing [J]. Mater Sci Eng A, 2002, 328: 317-323.
[17] JON A, JAVIER G S. A comparison of FEM and upper-bound type analysis of equal-channel angular pressing (ECAP) [J]. J Mater Proc Technol, 2003, 141: 313-138.
[18] PRANGNELL P B, HARRIS C, ROBERTS S M. Finite element modeling of equal channel angular extrusion [J]. Scripta Mater, 1997, 37: 983-989.
[19] DONG H S, PAK J J, YOUNG K K, et al. Effect of pressing temperature on microstructure and tensile behavior of low carbon steels processed by equal channel angular pressing[J]. Mater Sci Eng A, 2002, 323: 409-415.
[20] KIM I, KIM J, SHIN D H, et al. Effects of equal channel angular pressing temperature on deformation structures of pure Ti [J]. Mater Sci Eng A, 2003, 342: 302-310.
[21] DUTTON R E, SEMIATIN S L, et al. Modeling of hot isostatic pressing and hot triaxial compaction of Ti-6Al-4V powder[J]. Acta Materialia, 1999, 47: 3159-3167.
[22] PEI Q X, HU B H, LU C, et al. A finite element study of the temperature rise during equal channel angular pressing [J]. Scripta Mater, 2003, 49: 303-307.
Corresponding author: ZHANG Xin-ping; Tel: +86-25-84315159; E-mail: zxp-0517@163.com


