
Single-atom spintronics
Susan Z. HUA, Matthew R. SULLIVAN, Jason N. ARMSTRONG
Materials Program, Mechanical and Aerospace Engineering Department, State University of New York at Buffalo, Buffalo, NY 14260, USA
Received 10 April 2006; accepted 25 April 2006
Abstract:
Recent work on magnetic quantum point contacts (QPCs) was discussed. Complete magnetoresistance loops across Co QPCs as small as a single atom was measured. The remarkable feature of these QPCs is the rapid oscillatory decay in magnetoresistance with the increase of contact size. In addition, stepwise or quantum magnetoresistance loops are observed, resulting from varying transmission probability of the available discrete conductance channels because the sample is cycled between the ferromagnetic (F) and antiferromagnetic (AF) aligned states. Quantized conductance combined with spin dependent transmission of electron waves gives rise to a multi-channel system with a quantum domain wall acting as a valve, i.e., a quantum spin-valve. Behavior of a few-atom QPC is built on the behavior of a single-atom QPC and hence the summarization of results as ‘single-atom spintronics’. An evolutionary trace of spin-dependent electron transmission from a single atom to bulk is provided, the requisite hallmarks of artefact-free magnetoresistance is established across a QPC – stepwise or quantum magnetoresistance loops and size dependent oscillatory magnetoresistance.
Key words:
quantum point contact; magnetoresistance; quantum domain wall; electron wave-guide; oscillatory magnetoresistance;
1 Introduction
As atoms aggregate to form a solid, the discrete electronic structure of an atom is eventually replaced by a quasi-continuous energy spectrum of electrons. Experiments on free clusters using the STERN-GERLACH method[1-2] in recent years have provided fundamental insight as to how the electronic structure evolves from a single atom to bulk[3-6]. For example, cluster studies reveal that the electronic structure of Ni and Co transitions from molecular-like (discrete) to bulk (quasi-continuous) when the respective number of Ni and Co atoms exceeds 10 and 20, marking the onset of appreciable s-d hybridization[7].
The first experiments on conductance across atomic point contacts were reported in Ag using the UHV STM[8]. Soon thereafter, observation of quantization of conductance was reported in Au, Pb, Ni, Cu, and Pt[9-12]. The study of quantized conductance in semiconductors and metals provides basic insight into the electronic structure[13-18]. In addition, the magnetic properties of materials reduced to a few atoms exhibit unusual behavior[19, 20]. They interact with the spin states of the transmitting electrons to modify the nature of quantized conductance. Magnetic transition metals can carry multiple conductance channels/atom, unlike simpler (monovalent) systems, such as gold, where each atom contributes one conductance channel[21]. Therefore, understanding the behaviour of magnetic multi-channel systems with quantized conductance is one of the fundamental problems of interest in spintronics as it provides an evolutionary trace of spin-dependent transport from a single atom to larger ensembles. In the study of such systems, there are many intricacies and subtleties that remain to be understood.
In 1999, a large ballistic magnetoresistance (BMR) effect was reported in Ni and Co quantum point contacts [22, 23]. These measurements were made using pulsed field excitations or minor loops. Measurement of minor magnetoresistance loops in slowly varying fields in Ni quantum point contacts was reported[24], along with a detailed discussion of magnetostriction related artefacts. More recently complete quantum magnetoresistance loops across Co QPCs have been measured[25]. A large magnetoresistance effect has also been reported in half-metal Fe3O4 oxide point contacts[26], where the mode of transport is tunnelling or hopping. In parallel with the experiments, a theoretical framework has also been built steadily, using both semi-classical[23] and quantum[27-29] approach. While the BMR effect with complete loops has also been measured in ballistic contacts a few nm in size, such contacts are too large for the observation of quantized steps in conductance [30-32]. Here recent results related to the measurement of complete magnetoresistance loops across Co atomic-sized contacts are focused primarily on[25]. These results are also distinguished from other studies on larger contacts by the quantization of conductance at which complete magnetoresistance loops have been measured. A remarkable and exciting feature of these quantum contacts is the rapid oscillatory decay in magnetoresistance with contact size. Quantized conductance combined with spin dependent transmission of electron waves gives rise to a multi-channel system with a quantum domain wall acting as a valve, i.e., a quantum spin-valve. The behavior of a few-atom QPC is built on the behavior of a single-atom QPC and hence the summarization of results as ‘single-atom spintronics’.
2 Experimental
Fig.1 shows a microfabricated templates made of Co thin film electrodes. The spacing between the Co electrodes in Fig.1 is typically 200-500 nm. High resistance <100> silicon wafers coated with an additional 1-2 mm thick silicon dioxide insulator layer were used in the microfabrication of the templates to suppress leakage currents through the substrate during subsequent electrodeposition and testing of the QPCs. Special microfabrication steps were taken to keep the gap between the patterned electrodes as small as possible in order to ensure that the electrodes were maximally constrained by the substrate. Photolithography was used to first form 0.4-0.5 mm deep channels on the silicon wafer by reactive ion etching[24]. A Ta (3 nm)/Co (10 nm) seed layer was then sputterly deposited inside the channels on which Co electrodes were subsequently electrodeposited. The 0.4-0.5 μm high channel walls initially restrict the lateral growth of the electrodes, and sufficiently thick Co electrodes (1-2 μm) with low resistance (3-5 Ω) could thus be electrodeposited. Thickening of the electrodes by electrodeposition of Co on the Ta/Co seed layer results in a small gap (<500 nm) between the electrodes, as shown in Fig. 1. Different electrode designs were tested, and four such template designs are shown in Fig.2(a)-(d).
Experimental procedures were carefully designed for minimal leakage current and to precisely control growth and measurement conditions. Microfabricated templates were made using high resistance <100> silicon wafers coated with an additional 1 mm thick silicon dioxide insulator layer to suppress possible leakage currents through the substrate. Details of microfabrication were given elsewhere[24]. Atomic point contacts were made at room temperature by electrodeposition of Co between two narrowly spaced (200-500 nm) microfabricated Co thin films 1-2 μm thick, using a cobalt sulfamate solution (75 g?L-1 Co as metal in Co(SO3NH2)2?2H2O; 30 g?L-1 boric acid, pH 3.2 to 3.3).

Fig.1 High-magnification SEM micrograph of a microfa-bricated template
The size of the contacts was controlled using a self-termination method[33], which is capable of forming stable contacts to a size-resolution of a single atom. Point contacts were formed by placing a drop of electrolyte on the microfabricated electrodes. The deposition voltage was between 0.6 and 1.0 V. High purity chemicals and solvents were used. Electrolytes were prepared in an inert atmosphere cage, using de-ionized ultra-filtered (DIUF) water. Prior to its use, DIUF water undergoes de-aeration by a thermal cycle to remove oxygen and other gases, followed by sparging for several hours until the dissolved oxygen in water could no longer be detected with the oxygen-electrode analyzer. The electrolytes were further filtered and sparged for several hours by argon. Additional steps in electrolyte preparation include low-current electroplating for a period of 24 h to rid the electrolyte of remaining residual impurities (i.e., electronic purification). The de-aerated DIUF water was also used for flushing the electrolyte upon formation of the contacts. Flushing was achieved in a cylindrical boat housing the sample with access for introducing and draining the liquids. As soon as the contact was formed, flushing of electrolyte by DIUF water commences in-situ by continuously filling and draining the boat to ensure that the electrolyte is completely washed away. The flushing process is based on control calibration runs needed to achieve the measured resistance across water to become experimentally indistinguishable from that of DIUF water to eliminate contamination. The whole flushing process typically lasts for 12-15 s. At all times during

Fig.2 SEM micrographs of different designs of microfabricated templates
this in-situ flushing process the sample remains submerged. The leakage currents across the electrodes of a template are measured using replacement water, and the leakage current is negligibly small in the pA range (10.79×10-12-86.57×10-12 A; standard devia-tion of 19×10-14-42×10-14 A; in applied voltages from 100-400 mV for a measured resistance across electrodes of GW. This leakage current is six orders of magnitude lower than the measured current through the contact. The subtraction of this leakage current from the I-V curves corresponds only to a sixth decimal point correction and is negligible. Magnetoresistance measurements were typically made at voltages between 100 to 350 mV (10-30 μA). The magnetoresistance loops were measured by cycling the samples in a magnetic field at a low cycling rate of 0.2 Hz.
3 Results and discussion
Electrodeposited cobalt point contacts remain stable for periods over a minute, as shown in Fig.3(a). A closer examination of the conductance plateaus obtained from hundreds of experiments reveals that the actual conductance value may differ or fluctuate slightly from the nominal value of conductance at a given plateau. For example, different contacts stabilized at a nominal value of 1Go (Go=2e2/h, where e is electron charge, h is PLANCK’s constant) were found to randomly take values ranging from approximately 0.85Go to 1.1Go, while contacts stabilized at the nominal 0.5Go conductance plateau assumed values were between about 0.37Go and 0.52Go, etc, as shown in inset-1 in Fig. 3(a). Small deviations from nominal values are well-studied [34] and result from interference (constructive or destructive) between the primary transmitted electron wave and the secondary waves arising from scattering in the diffusive banks. Presence of a domain wall across a contact made of a magnetic atom can lead to a further deviation from the nominal conductance value as discussed in the following. Contacts formed by mechanical methods are typically stable for periods of ms to ms and a large amount of statistics has to be gathered from mechanically unstable contacts as they break to infer the peaks in quantized conductance. Contacts shown in Fig.3(a) remain stable for periods over a minute and naturally show the quantized conductance plateaus and deviations taken by the system, thereby obviating an indirect inference through a statistical compilation of a histogram using a large number of transient traces (and furthermore the two were found to be equivalent in the present study).
A narrow spread in the statistical distribution in the conductance for contacts shown in Fig.3(a) is evident from inset-2 in Fig.3(a). Contacts at lower Go (<3Go= were stable for periods up to 2-3 min, while contacts at higher Go were stable for periods ranging from 10 min to 1 h. Note that the use of the term ‘stable’ here is relative, consistent with the term ‘stable’ in the past[24], and the fact that atomic point contacts reported by others in the literature typically last for short times was given.
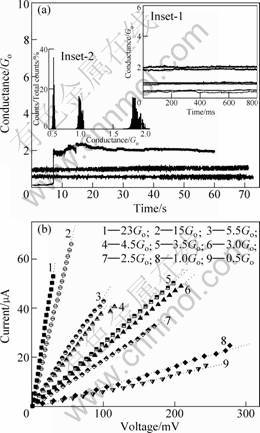
Fig.3 Electrical properties of cobalt quantum point contacts of various sizes, with contacts in the spin-split state formed in the presence of a constant magnetic field of approximately 48 kA/m: (a) Conductance traces for cobalt point contacts at nominal values of 0.5Go, 1Go and 2Go; where 1Go=2e2/h=7.748 091×
10-5 siemens=1/12 906 Ω-1; e is electron charge and h is Planck’s constant. Slight deviations in the measured conductance from the nominal values of respective conductance plateaus are shown in inset-1 for six different cobalt contacts, two each for contacts stabilized at or near the nominal values of 0.5Go, 1Go and 2Go. Inset-2 shows the statistical spread corresponding to the three conductance traces in the red solid curves in inset-2(shown in Fig.(a)) are the Gaussian fit to the distributions. (b) Current-Voltage (I-V) curves at various contact sizes as small as a single atom, and with or without spin-splitting. The dotted line shows the linear fit to the measured I-V curves. ‘Size’ refers to the cross-section of the contact, expressed in terms of quantized value of its conductance
Electrodeposited cobalt point contacts of all sizes were found to have linear current-voltage (I-V) characteristics, shown in Fig.3(b). Within the range of applied voltages, only a negligible deviation from linearity was found. Conditions leading to linear or non-linear I-V curves depend on the experimental conditions and have recently been studied and reviewed[34, 35]. A systematic comparison of the I-V curves in quantum point contacts for a range of surface conditions, from clean surfaces verified by scanning tunneling microscope imaging, surfaces produced by sputtering and annealing in ultra-high vacuum, to intentional contamination was made. For contacts exposed to air, with an oxide layer, or with contamination, non-linear curves are almost exclusively found. In sharp contrast, for clean metal contacts, such as in the present study, linear behaviour is the norm. Moreover, as described in the Methods section, the directly measured leakage currents were negligible (pA), and have no measurable effect on the linearity of the I-V curves shown in Fig.3(b). While the atomic size of these contacts and their short lifetimes prevent their direct imaging by transmission or scanning electron microscopy, the value of the quantized conductance is an electronic way to determine their size since it is the narrowest region of the contact that alone determines the available modes. Nonetheless, it is still possible to image and gain insight on the nature of the growth morphology after the contact is broken, shown in Fig.4.

Fig.4 Low magnification scanning electron microscope image of the microfabricated electrodes between which a cobalt point contact of 0.5Go conductance was electrodeposited. A tip was intentionally microfabricated on one of the two electrodes (shown encircled) in order to concentrate the electric field for preferential electrodeposition of the contact across it. Inset shows a high-magnification image of the growth morphology. The actual contact broke prior to imaging and only a gap (instead of the contact) can be seen between the two electrodes in the magnified image
It can be observed that as-deposited quantum point contacts show either a spontaneous antiferromagnetic (AF) or ferromagnetic (F) coupling across the contact depending on its size. The AF aligned state results in the formation of a domain wall across the contact, which in turn alters the number of available channels for conductance with respect to the F-aligned state. In other words, the electron transmission probability for F and AF states is different and therefore field-dependent. The field-dependent opening and closing of conductance channels manifest itself as discrete or quantum magnetoresistance loops, such as the one shown in Fig.5(a) for a contact having a nominal saturation conductance of 3Go. Following saturation in the positive direction, Fig.5(a) shows that as the field strength is reduced to zero, the resistance remains constant. Only when the field goes past zero in the negative direction, the resistance increases corresponding to spontaneous reversal of magnetization from the F to AF aligned state, leading to the formation of an atomically abrupt domain wall across the contact, and the measured magnetoresistance is 85%. Unlike conventional domain walls that are hundreds of nm in width, ‘constrained’ or ‘quantum’ domain walls across these atomic point contacts are atomically abrupt[36-40]. In Fig.5(a), the high-resistance plateau persists, until the field reaches -10.4 kA/m at which point the alignment of magnetization across the contact begins to change. However, the resulting decrease in resistance is not continuous with field. Instead, a ‘digital’ or stepwise change in resistance is observed where portions of the loop are field-independent, followed by a drop in resistance to the next resistance plateau, shown in Fig.5(a). Stepwise change in magnetoresistance is a unique feature of these atomic point contacts with quantized conductance, in contrast to a continuous change in magnetoresistance oflarger contacts[30-32] where only ballistic transport prevails. When the field reaches negative saturation, the magnetization alignment across the contact becomes parallel, and the resistance at negative saturation becomes equal to the resistance at positive saturation. As the field strength is reduced from negative saturation back to zero, the resistance remains constant and field-independent since in this segment of the hysteresis loop no domain wall is present across the contact. Only when the field is cycled past zero and increased in the positive direction, the resistance rises when the magnetization vectors across the contact flip in the anti-parallel direction leading to the formation of a quantum domain wall across the contact. The effect of the resulting domain wall in applied magnetic field is the same as that described for the negative field cycle, and at a sufficiently high field the resistance reversibly returns back to its starting value. The observed spin-valve like behaviour in Fig.5(a) as a function of applied field results from a change in the number or probability of the transmitting channels due to a quantum domain wall across the atomic point contact. Even though minor loop or pulsed excitation measurements have been previously reported [22, 24], measurement of complete quantum magnetoresistance loops in atomic point contacts naturally set themselves apart from mechanical artefacts without the need for any additional empirical evidence.
This is because the change in resistance arising from magnetic artefacts (magnetostriction or magnetostatic distortions) behave the same way in either field direction, rather than showing a field-dependent segment of resistance from zero to positive (or zero to negative) saturation and a field-independent segment of resistance upon returning from positive (or negative) saturation back to zero where the domain wall is absent. In other words, the change in resistance with applied field clearly depends on the presence or absence of the domain wall across the contact. Corresponding to both halves of the loop in Fig. 5 (a), the system takes an equal number of steps going from either zero to negative, or from zero to positive saturation, and the values of these steps are virtually identical, as shown in Fig.5(b).
In a metal point contact joining the two electrodes, where the FERMI wavelength is 0.5 nm or less, the behaviour of propagating electrons can be expressed by transversely confined and freely propagating longitudinal wave-functions. The transverse confinement of the electron wave functions (modes) by the contact size gives rise to discrete sub-bands or channels, shown in Fig.5(c), within which the parabolic momentum terms represent the contribution due to the free propagation along the longitudinal direction. The integration over all available channels gives rise to the observed conductance. The presence of an abrupt domain wall across the contact in Fig.5(b) causes the number of transmitting channels to differ between AF and F aligned states, giving rise to a stepwise change in magnetoresistance. As the size of the contact increases, the ‘abrupt’ domain wall gradually broadens and the number of available channels increases, causing the quantum effect to diminish rapidly.
Following the measurement of the magnetoresistance loop across the 3Go contact, the contact was grown in size to the next higher conductance plateau at 4Go. The hysteresis characteristics of the larger contact(shown in Fig.5(d)) are similar to those described in Fig. 5(a). However, an increase in conductance by just one quantized level causes the magnetoresistance to drop to only 25%. When the contact is grown to the next higher conductance plateau of 5Go, the magnetoresistance essentially vanishes, shown in Fig.5(e). The trend shown in Figs.5(a) and 5(d)-(e) points to enhanced magnetoresistance for contacts stabilized at progressively smaller conductance plateaus where the effect of the quantum domain wall is most prominent. The smallest conductance plateau at which Co can be stabilized is 1Go, the signature of quantized conductance across a single atom. Complete magnetoresistance loops across atomic-sized contacts were measured, and the typical magnetoresistance for such contacts approaches about 300%, shown in Fig.5(f).
The dependence of magnetoresistance on the contact size was systematically studied. While results in point shown in Fig.5 to an overall decay in magnetoresistance with the increase of contact size, the
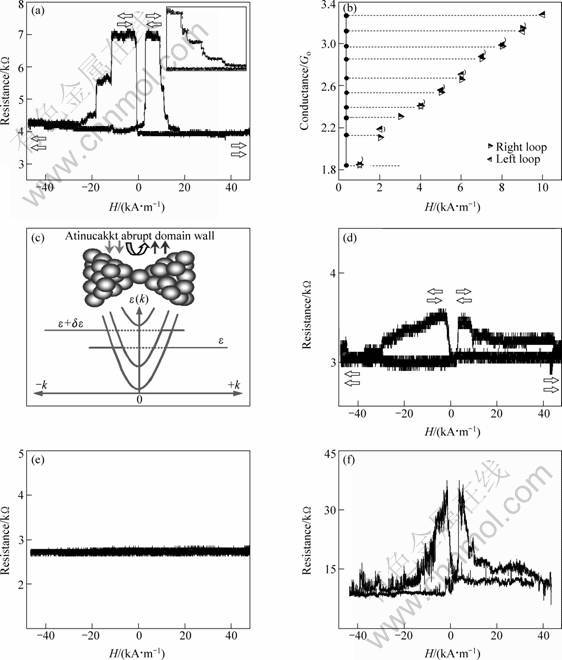
Fig.5 Quantum magnetoresistance loops showing stepwise change in resistance with applied magnetic field in cobalt point contacts of various sizes along with an illustration of discrete conductance channels due to the transverse confinement of electron waves. (a) Magnetoresistance loop of a cobalt point contacts having a nominal value of 3Go at saturation. Discrete or stepwise nature of quantum magnetoresistance in the atomic point contact is highlighted in the inset for a section of the magnetoresistance loop in the positive field quadrant. (b) Values of stepwise conductance taken by the system corresponding to the magnetoresistance curve in (a). The blue and red arrows correspond to the observed steps in the magnetoresistance loop in (a), for the positive and negative field directions, respectively. (c) Schematic of an atomically abrupt quantum domain wall across a point contact and discrete energy levels or ‘channels’ due to the transverse confinement of the electron waves. The direction of applied magnetic field is in the horizontal direction along the axis of the contact. Curves in (d)-(f), shows the magnetoresistance loop of cobalt point contacts with nominal values of 4Go, 5Go, and about 1Go at saturation, respectively
exciting and remarkable feature of these quantum contacts is the reflection of a rapid oscillatory decay in magnetoresistance with the increasing contact size, shown in Fig.6.
Four distinct peaks in magnetoresistance were observed. The periodicity of the first few oscillations is on the order of atomic dimensions. In all experiments no measurable magnetoresistance at the minima of the oscillations was ever found. The existence of oscillations in magnetoresistance with the increase of contact size are a result of change in the strength of exchange field across quantum domain walls. The oscillatory nature of magnetoresistance can be observed only by the measurement of complete magnetoresistance loops and on atomic sized contacts with quantized conductance, and not in larger systems.
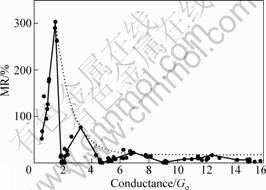
Fig.6 Oscillatory nature of magnetoresistance as a function of quantized conductance in the high field (ferromagnetic aligned) state. Each point corresponds to an individual magnetoresistance loop. The solid blue line is drawn only as an aid for the eyes to trace the oscillations. The dashed line is an exponential decay fit to the four maxima in magnetoresistance versus contact size
Previously magnetoresistance versus contact size plots were developed using pulsed measurements or minor loops[22, 23], which only yield a rapid decay with a large scatter, and no quantum oscillations have ever been observed, considered or noticed[22, 23, 41-43]. While the overall decay in magnetoresistance can be explained by semi-classical domain wall scattering theory [23], such models do not predict the observed oscillatory behaviour. Oscillatory magnetoresistance as a consequence of conductance quantization was proposed by IMAMURA[27] adapting SCHILLING’s idea of a quantum domain wall with atomically abrupt magnetization gradient[44], and further elaborated by TAGIROV[28]. In this model, spin precession across the quantum domain wall is forbidden and the shape of the domain wall remains unchanged upon increasing the contact size. The oscillations arise from a sudden change in the number of open conductance channels at certain sizes of the constriction. The role of the quantum domain wall is to change the number of transmitting channels, producing peaks in magnetoresistance. These models provide a theoretical explanation for the observed oscillations in magnetoresistance shown in Fig.7. Further theoretical work is clearly needed in order to understand the effect of contact shape, Fermi-momenta of the conduction spin sub-bands, and exchange splitting of the conduction band as they are of fundamental interest.
As for the ultimate application of magnetoresistance in quantum point contacts, “The use of point contacts was just for convenience, proof of principle”[45]. It was the Sandwich geometry that ultimately led to the transistor revolution.
4 Conclusions
Complete quantum magnetoresistance loops were measured in atomic sized Co point contacts. The remarkable feature of these quantum contacts is that the oscillatory nature of magnetoresistance is as a function of contact size. In addition, spin valve-like magnetoresistance loops and size-dependent quantum oscillations conclusively prove the electronic nature of the observed quantum magnetoresistance effect and naturally eliminate all artefact interpretations such as a mechanical on-off relay due to magnetostriction or magnetostatic forces. These results are also distinguished from other studies on larger contacts by the quantization of conductance at which magnetoresistance is measured. Transmission through multiple channels of a magnetic single atom regulated by a quantum domain wall forms a quantum spin valve.
Acknowledgments
This work is supported by NSF-DMR-FRG-03-
05242, and this support is gratefully acknowledged. Authors thank professor Harsh Deep Chopra for useful discussions. We thank Daniel ATEYA for help in microfabrication of the templates. The authors acknowledge Peter BUSH, South Campus Instrumenta-
tion Center, for help with SEM imaging of the contacts. Microfabrication is performed, in part, at the Cornell Nanofabrication Facility, which is supported by the NSF Grant ECS-9731293, Cornell University, and industrial affiliates. The authors thank Lev DERESH and David LASHMORE for suggestions on electrochemistry, and Larry BENNETT for pointing to the history of point contact transistors.
References[1] GERLACH W, STERN O. Der experimentelle nachweis des magnetischen moments des silberatoms[J]. Z Phys, 1922, 8: 110-111.
[2] FRIEDRICH B, HERSCHBACH S G. How a bad cigar helped reorient atomic physics[J]. Phys Today, 2003: 53-66.
[3] REUSE F A, KHANNA S N. Geometry, electronic structure, and magnetism of small Nin(n=2-6, 8, 13) clusters[J]. Chem Phys Lett, 1995, 234: 77-81.
[4] YANG C Y, JOHNSON K H, SALAHUB D R, KASPAR J, MESSMER R P. Phys iron clusters: electronic structure and magnetism[J]. Rev B, 1981, 24: 5673-5692.
[5] FUJIMA N, YAMAGUCHI T. Magnetic moment in Ni clusters estimated by an electronic-shell model[J]. Phys Rev B, 1996, 54: 26-28.
[6] LEE K, CALLAWAY J, KWONG K, TANG R, ZIEGLER A. Electronic structure of small clusters of nickel and iron[J]. Phys Rev B, 1985, 31: 1796-1803.
[7] LIU S, ZHAI H, WANG L. s-d hybridization and evolution of the electronic and magnetic properties in small Co and Ni clusters[J]. Phys Rev B, 2002, 65: 113401-113404.
[8] GIMZEWSKI G K, M?LLER R. Transition from the tunneling regime to point contact studied using scanning tunneling microscopy[J]. Phys Rev B, 1987, 36: 1284(R)-1287(R).
[9] PASCUAL J I, et al. Quantum contact in gold nanostructures by scanning tunneling microscopy[J]. Phys Rev Lett, 1993, 71: 1852-1855.
[10] KRANS J M, VAN RUITENBEEK J M, FISUN V V, YANSON I K, DE JONGH L J. The signature of conductance quantization in metallic point contacts[J]. Nature, 1995, 375: 767-769.
[11] OLESEN L, et al. Quantized conductance in an atom-sized point contact[J]. Phys Rev Lett, 1994, 72: 2251-2254.
[12] BRANDBYGE, et al. Quantized conductance in atom-sized wires between metals[J]. Phys Rev B, 1995, 52: 8499-8514.
[13] WHARAM D A, et al. Addition of the one-dimensional quantised ballistic resistance[J]. J Phys, 1988, C21: L887-L891.
[14] VAN WEES B J, et al. Quantized conductance of point contacts in a two-dimensional electron gas[J]. Phys Rev Lett, 1988, 60: 848-850.
[15] VON KLITZING K, DORDA G, PEPPER M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance[J]. Phys Rev Lett, 1980, 45: 494-497.
[16] FOWLER A B, FANG F F, HOWARD W E, STILES P J. Magneto-oscillatory conductance in silicon surfaces[J]. Phys Rev Lett, 1966, 16: 901-903.
[17] LANDAUER R Spatial variation of currents and fields due to localized scatterers in metallic conduction[J]. IBM J Res, 1957, 1: 223-231.
[18] B?TTIKER M, IMRY Y, LANDAUER R, PINHAS S. Generalized many-channel conductance formula with applications to small rings[J]. Phys Rev, 1985, B31: 6207-6215.
[19] MADHAVAN V, CHEN W, JAMNEALA T, CROMMIE M F, WINGREEN N S. Tunneling into a single magnetic atom: spectroscopic evidence of the Kondo resonance[J]. Science, 1998, 280: 567-569.
[20] GAMBERDELLA P, et al. Giant magnetic anisotropy of single cobalt atoms and nanoparticle[J]. Science, 2003, 300: 1130-1133.
[21] SCHEER E, et al. The signature of chemical valence in the electrical conduction through a single-atom contact[J]. Nature, 1998, 394: 154-157.
[22] GARC?A N, MU?OZ M, ZHAO Y W. Magnetoresistance in excess of 200% in ballistic Ni nanocontacts at room temperature and 100 Oe[J]. Phys Rev Lett, 1999, 82: 2923-2926.
[23] TATARA G, ZHAO Y W, MU?OZ M, GARC?A N. Domain wall scattering explains 300% ballistic magnetoconductance of nanocontacts[J]. Phys Rev Lett, 1999, 83: 2030-2033.
[24] SULLIVAN M R, BOEHM D A, ATEYA D A, HUA S Z, CHOPRA H D. Ballistic magnetoresistance in nickel single-atom conductors without magnetostriction[J]. Phys Rev, 2005, B71: 024412(1) -024412(8).
[25] CHOPRA H D, SULLIVAN M R, ARMSTRONG J N, HUA S Z. Nature Materials, 2005, 4: 832-837.
[26] VERSLUIJS J J, BARI M A, COEY J M D. Magnetoresistance of half-metallic oxide nanocontacts[J]. Phys Rev Lett, 2001, 87: 026601(1)-026601(4).
[27] IMAMURA H, KOBAYASHI N, TAKAHASHI S, MAEKAWA S. Conductance quantization and magnetoresistance in magnetic point contacts[J]. Phys Rev Lett, 2000, 84: 1003-1006.
[28] TAGIROV L R, VODOPYANOV B P, EFETOV K B. Multivalued dependence of the magnetoresistance on the quantized conductance in nanosize magnetic contacts[J]. Phys Rev, 2002, B65: 214419(1) -214419(7).
[29] VELEV J, BUTLER W. Domain-wall resistance in metal nanocontacts[J]. Phys Rev, 2004, B69: 094425(1)-094425(6).
[30] GARC?A N, et al. Ballistic magnetoresistance in a magnetic nanometer sized contact: An effective gate for spintronics[J]. Appl Phys Lett, 2001, 79: 4550-4552.
[31] CHOPRA H D, HUA S Z. Ballistic magnetoresistance over 3000% in Ni nanocontacts at room temperature[J]. Phys Rev, 2002, B66: 020403R1-020403R3.
[32] HUA S Z, CHOPRA H D. 100 000% ballistic magnetoresistance in stable Ni nanocontacts at room temperature[J]. Phys Rev, 2003, B67: 060401R1-060401R4.
[33] BOUSSAAD S, TAO N J. Atom-size gaps and contacts between electrodes fabricated with a self-terminated electrochemical method[J]. Appl Phys Lett, 2002, 80: 2398-2400.
[34] AGRA?T N, YEYATI A L, VAN RUITENBEEK J M. Quantum properties of atomic-sized conductors[J]. Phys Rept, 2003, 377: 81-279.
[35] HANSEN K, et al. Current-voltage curves of gold quantum point contacts revisited[J]. Appl Phys Lett, 2000, 77: 708-710.
[36] BRUNO P. Geometrically constrained magnetic wall[J]. Phys Rev Lett, 1999, 83: 2425-2428.
[37] LABAYE Y, BERGER L, COEY J M D. Domain walls in ferromagnetic nanoconstriction[J]. J Appl Phys, 2002, 91: 5341-5346.
[38] MOLYNEUX V A, OSIPOV V V, PONIZOVSKAYA E V. Stable two- and three-dimensional geometrically constrained magnetic structures: The action of magnetic fields[J]. Phys Rev, 2002, B65: 184425(1)-184425(6).
[39] JUBERT P O, ALLENSPACH R, BISCHOF A. Magnetic domain walls in constrained geometries[J]. Phys Rev, 2004, B69: 220410(1) -220410(4).
[40] KAZANTSEVA N, WIESER R, NOWAK U. Transition to linear domain walls in nanoconstrictions[J]. Phys Rev Lett, 2005, 94: 037206(1)-037206(4).
[41] CHUNG S H, MU?OZ M, GARC?A N, EGELHOFF W F, GOMEZ R D. Universal scaling of ballistic magnetoresistance in magnetic nanocontacts[J]. Phys Rev Lett, 2002, 89: 287203(1) -287203(4).
[42] CHUNG S H, MU?OZ M, GARC?A N, EGELHOFF W F, GOMEZ R D. Universal scaling of magnetoconductance in magnetic nanocontacts(invited)[J]. J Appl Phys, 2002, 93: 7939-7944.
[43] GARC?A N, et al. Ballistic magnetoresistance in different nanocontact configurations: a basis for future magnetoresistive sensors[J]. J Magn Magn Mater, 2002, 240: 92-99.
[44] SCHILLING R. Quantum theory of domain walls[J]. Phys Rev, 1977, B15: 2700-2703.
[45] RIORDAN M, HODDESON L. Crystal fire, the Birth of the Information Age[M]. New York: W W Norton & Company, 131.
Corresponding author: Susan Z. HUA; E-mail: zhua@eng.buffal.edu


