
J. Cent. South Univ. (2019) 26: 873-880
DOI: https://doi.org/10.1007/s11771-019-4056-0

An innovative method to calculate oxygen consumption rate
YIN Wen-tao(殷文韬)1, 2, SONG Ze-yang(宋泽阳)3
1. National Institute for Occupational Safety, Beijing 100029, China;
2. Beijing Municipal Institute of Labour Protection, Beijing 100054, China;
3. College of Safety Science and Engineering, Nanjing Tech University, Nanjing 210009, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract:
Based on heat and mass transfer characteristics of spontaneous combustion of coal, Arrhenius equation and the Ranz-Marshall correlation, a novel approach was proposed in this paper to estimate oxygen consumption rate of self-ignition of coal at high temperature. Compared with the conventional methods, this approach involves not only kinetic properties of self-ignition of coal and temperature, but also the ambient air flow characteristics and diameter of coal particle. To testify the proposed approach, oxygen consumption rates at high temperature were measured by the programmable isothermal oven experiments. Comparisons between experimental and theoretical results indicate that the rates of oxygen depletion calculated by the proposed approach agree well with those measured from laboratory-scale experiments, which further validates the proposed approach.
Key words:
Cite this article as:
YIN Wen-tao, SONG Ze-yang. An innovative method to calculate oxygen consumption rate [J]. Journal of Central South University, 2019, 26(4): 873–880.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-019-4056-01 Introduction
Spontaneous combustion of coal refers to a physical and chemical process of exothermic oxidation reaction at low-temperature, which leads to self-heating at the beginning and thermal runaway ultimately. If the heat produced by low-temperature reaction is not sufficiently dissipated to the surrounding environment by means of conduction or convection, it results in a temperature increase and a higher rate of oxidation reaction [1–4]. When the temperature exceeds the threshold value (80–120 °C), thermal runaway occurs and the coal then ignites spontaneously [4–6]. Self-ignition of coal occurs widely in industries which results in various forms of hazards like coal fires in mine goaf [5, 7, 8], coal stockpile [4, 9–12] and underground coal seam [13–15]. Spontaneous combustion of coal leads to loss of precious coal resources and emission of greenhouse gases, such as carbon dioxide and methane, and other toxic gases, and also threatens the health of local inhabitants [16]. Underground coal seam fires even result in perilous land subsidence and vegetation deterioration [13, 14].
Oxygen consumption rate is a key parameter to represent spontaneous combustion of coal. But it is difficult to precisely calculate or directly measure the rate of oxygen consumption of spontaneous combustion of coal. In general, two experiential approaches are adopted to estimate oxygen consumption rate of self-heating or self-ignition of coal. Arrhenius equation is a theoretical method widely used to estimate oxygen consumption rate [9, 12, 17]. But kinetic parameters in Arrhenius equation, i.e., pre-exponential factor (A) and activation energy (E), are obtained from experiments including programmable isothermal oven [7, 18], adiabatic calorimeters [19, 20] and thermogravimetric analysis [21]. The other method is experimental method (like the programmable isothermal oven experiment) to measure oxygen concentration changes during the process of self-ignition. These two methods mainly focus on coal properties associated with spontaneous combustion. However, apart from effects of coal properties, oxygen consumption of spontaneous combustion of coal is also impacted by external factors such as oxygen transport, and diameter of coal particle. In some cases, the external factors may have greater influence on oxygen depletion rate than coal properties [22]. For instance, the rate of oxygen consumption exponentially increases with temperature. Under natural convection conditions, oxygen consumption is controlled by oxygen transport when oxygen consumption rate is faster than oxygen transport rate because oxidation reaction will merely proceed as long as sufficient oxygen is transported to self-ignition coal [23].
However, these issues have rarely been considered in estimating oxygen consumption rate at high temperature. Our main aims are to deal with the paradoxical situation between oxygen consumption and oxygen transport at high temperature and propose a novel formula of oxygen consumption rate at high temperature involving coal properties, temperature, oxygen transport and diameter of coal particle. The programmable isothermal oven experiments are conducted to validate our proposed approach.
2 Theoretical model
2.1 Timescale and critical temperature
Wessling used the timescales to illustrate the paradoxical situation mentioned above between oxygen consumption and oxygen transport [23]. The timescale formulations of kinetic oxygen depletion and oxygen transport can be written as Eqs. (1) and (2).
 (1)
(1)
 (2)
(2)
where τr and τt denote timescales in the units of s of kinetic oxygen depletion and oxygen transport, respectively. A and E are pre-exponential factor (s–1) and activation energy (J/mol), respectively. R is the ideal gas constant (J/(mol·K)). T and Ta are temperature and ambient temperature, respectively. l is the representative length of the oxygen concentration decrease in the unit of m [23]. ε and K stand for porosity and permeability of coal (m2), respectively. μ is dynamic viscosity of air flow (kg/(m·s)). ρ and g denote density and gravitational acceleration, respectively.
As shown in Figure 1, timescales of both kinetic reaction and oxygen transport are equal when temperature is approximately 480 K. This temperature is called the critical temperature Tc. Timescale of kinetic reaction is larger (smaller) than that of oxygen transport if temperature is lower (higher) than the critical temperature, which indicates that oxygen consumption rate is slower (faster) than oxygen transport rate while temperature is lower (higher) than the critical temperature. Therefore, if T<>c, oxygen consumption rate is controlled by the kinetic reaction because the amount of oxygen transported meets the amount of oxygen needed by kinetic oxidation of coal; if T>Tc, oxygen consumption rate is dominated by oxygen transport because oxidation reaction will merely proceed as long as sufficient fresh oxygen is transported to self-ignition coal. In Figure 1, kinetic parameters to calculate τr are obtained from the programmable isothermal oven experiment: E=33995.22 J/mol and A=19952.02 s–1. Coal samples were collected from Jinggezhuang Coal Mine in Tangshan City of Hebei Province. Parameters’ value in Eq. (2) to compute τt: l=0.08 m,ε=0.2, K=5×10–8 m2, μ=2×10–5 kg/(m·s), and Ta=300 K.

Figure 1 Temperature-dependent timescales of kinetic oxygen consumption (τr) and oxygen transport (τt)
2.2 Oxygen consumption rate at high temperature
As mentioned in Section 1, self-ignition is a complicated oxidation process and a variety of factors affect the rate of oxygen consumption. Therefore, it is necessary to make some assumptions to simplify the model of self-ignition of coal. Modeling oxygen consumption rate at high temperature is based on the following assumptions:
1) Coal and its ambient air associated with self-ignition reaction consist of a system, i.e., the object of our research. Temperature, oxygen concentration and remained oxygen concentration described in this paper denote temperature and oxygen concentration in this system.
2) Denotes that temperature is higher than the critical temperature Tc; the oxygen concentration consumed equals the oxygen concentration transported at, which indicates that remained oxygen concentration (after oxidation reaction between coal and oxygen) equals zero mol/m3 when T≥Tc.
3) Oxygen is transported by thermal buoyancy (natural convection) or the rate of forced oxygen transport is slow;
4) Because the rate of gas flow in the combustion zone is very slow (10–6–10–4 m s–1), the gas flow in the combustion zone is laminar flow and the mass transfer rate is equal to the heat transfer rate, i.e. Sh (Sherwood number)=Nu (Nusselt number).
At, the oxygen concentration consumed equals the oxygen concentration transported [24], which yields
 (3)
(3)
where c and cs are oxygen concentrations (mol/m3) in the ambient (boundary of coal particle) and the burning coal particle, respectively. The right-hand term r*(c–cs) is the oxygen transport rate, which is proportional to the oxygen concentration gradient (c–cs) between the ambient and the burning coal particles. Here, we define r* as the “modified mass transport coefficient”, the reciprocal of the oxygen transport timescale, in the unit of s–1. In Eq. (3), the oxygen concentration in the burning coal particles (cs) and the modified mass transport coefficient (r*) are two unknown variables. The oxygen depletion rate can be derived if another equation in terms of these two variables is established.
Apparently, the modified mass transport coefficient (r*) is proportional to the mass transfer coefficient (k), which has units of m/s. In addition, according to Eq. (2), timescale of oxygen transport is proportional to the representative length of oxygen concentration decrease (l), which indicates that the longer l is, the slower oxygen transport is. Therefore, the “modified mass transport coefficient” is inversely proportional to the representative length of oxygen concentration decrease (l). Then, we obtain
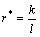 (4)
(4)
where k is the mass transfer coefficient, which can be described as
 (5)
(5)
where D and d are diffusion coefficient (m2/s) and diameter of coal particle, respectively.
A heat transfer correlation for sphere is given by the Ranz-Marshall Correlation [24]:
 (6)
(6)
where Pr and Re are Prandtl number and Reynolds number, respectively. Substituting Nu from Eq. (6) into Eq. (5) and k from Eq. (5) into Eq. (4),
 (7)
(7)
By reorganizing Eq. (3), we can obtain the formulation of cs as a function of r*.
 (8)
(8)
Substituting both cs and r* from Eqs. (8) and (7) into Eq. (3), the estimated oxygen consumption rate is
 (9)
(9)
For coal with porosity ε (like coal in mine goaf and coal stockpiles), oxygen consumption rate of spontaneous combustion is modified into
 (10)
(10)
3 Experimental
In order to validate the proposed formula of oxygen consumption rate at high temperature, the programmable isothermal oven experiments are conducted in the State Key Laboratory of Coal Resources and Safety Mining of China University of Mining and Technology (Beijing). The basic setup of the experiment is briefly illustrated in the following [6, 7, 18].
This experimental system is separated into three parts: air supply system, programmable isothermal oven, and exhaust gas chromatograph system, as shown in Figure 2. The oven temperature can be held constant from 35 to 200°C, within an accuracy of ±0.5°C. The rate of oven temperature increase is 1°C per minute. First, the oven should be turned on and preset at 15°C. After the isothermal condition is reached in the oven, a stainless steel cylindrical container (7 cm diameter and 10 cm high) filled with the coal sample (approximately 200 g) is placed in the center of the oven. Three thermocouples are placed at the center of the container. Gas air or nitrogen from a compressed gas cylinder is transported into the bottom container and exits from the top, allowing coal sample in the container to be sufficiently oxidized. The gas transport rate is flexible. In our experiments, gas transport rate is set as 1×10–6 m/s (60 mL/min) to agree with the second assumption of our theoretical model. The gas is preheated to the oven temperature by heat exchange coils in the oven. The coal sample is exposed to a flow of dry nitrogen to prevent coal oxidation before the coal sample reaches the oven temperature. The exhaust gas concentrations including carbon monoxide (CO) and carbon oxide (CO2) and remained oxygen concentration are measured continuously using gas chromatograph system. Coal sample temperature detected by thermocouples is recorded by data acquisition. In order to simulate oxygen consumption of self-ignition of coal samples at (viz. kinetic reaction faster than oxygen transport and oxygen consumption rate controlled by oxygen transport as mentioned in Section 2.2), remained oxygen concentration exits from the top of the oven should be lower than 0.9 mol/(m3·s) (less than 1% mole percentage of exhaust gases) before the test terminates. This condition suggests that oxygen concentration transported into coal sample is almost consumed by kinetic reaction and further is in line with the first assumption of the theoretical model. Two coal samples collected from the Jinggezhuang Coal Mine (1#) and Qianjiaying Coal Mine (2#) of Kailuan Group were tested. Proximate and ultimate analyses of two coal samples are represented in Table 1.
4 Results and discussion
Workflow of result analysis and validation of the theoretical model is shown in Figure 3. Based on the experimental parameters and oxygen concentration, the rate of oxygen consumption is calculated by the following equation [7, 18]:
 (11)
(11)
where v denotes air flow rate in the container (m/s); L is the height of the container; c0 and cc are oxygen concentrations in the ambient and the container, (mol/m3). According to the calculated oxygen consumption rate r and its corresponding experimental temperature T, kinetic parameters i.e., pre-exponential factor A and activation energy E can be given by [5]
 (12)
(12)
According to Eq. (12), kinetic parameters of two coal samples are calculated as shown in Table 2,which agree with published experimental results [17].

Figure 2 Schematic of experimental setup and measurement of programmable isothermal oven referred to [6, 35]
Table 1 Proximate and ultimate analyses of two coal samples
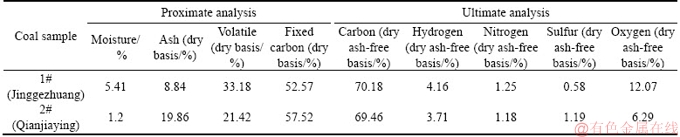

Figure 3 Summarized workflow of validation of proposed theoretical model
Table 2 Calculated kinetic parameters of two coal samples based on programmable isothermal oven experiments

Although at the end of experiments oxygen concentration emitted from the container is very low (1# coal sample: 0.95% mole fraction; 2# coal sample: 0.97% mole fraction), it is difficult for oxygen concentration to drop to 0 mol/m3 as shown in Figure 4 because of the limitations of the programmable isothermal oven. Thus the critical temperature (i.e., coal sample temperature while oxygen concentration is 0 mol/m3) can not be directly obtained from experimental results. However, the critical temperature (Tc) can be indirectly deduced from experimental data associated with oxygen concentration and coal sample temperature using curve fitting approach. Take 1# coal sample for example, as shown in Figure 4, evolution of coal sample temperature with oxygen concentration is fitted by three orders of polynomial function:
T=498.08–57.04009c+10.58497c2–0.70988c3(13)
As can be seen from Figure 4 and Eq. (13), the critical temperature is the intercept of the fitted polynomial function, i.e. Tc=f(c=0), as shown in Figure 3. Thus, for 1# coal sample, Tc=498.08 K. The critical temperature of 2# coal sample can be obtained using the same approach: Tc=483.88 K.

Figure 4 Evolution of coal sample temperature with oxygen concentration in container and its fitted curve to deduce critical temperature Tc
Evolution of oxygen consumption rate with coal sample temperature can also be deduced using the curve fitting method [7, 18]. The fitted functions (r=f(T)) of 1# and 2# coal samples are shown in Eqs.(14) and (15), respectively.
r=2.66393–0.02043T+5.04092×10–5T2–3.9.436×10–8T3 (14)
r=–210.61+2.77158T–0.01446T2+3.7387×10–5T2–4.78899×10–8T4+2.43111×10–11T5 (15)
As can be seen in Figure 3, oxygen consumption rates of experiments of two coal samples at the critical temperature, which start to be controlled by oxygen transport, can be derived by Eqs. (14) and (15), i.e., points A as shown in Figures 5 and 6. Correspondingly, oxygen consumption rates of theoretical model of two coal samples at the critical temperature are calculated by kinetic parameters as shown in Table 2 and Eq. (10), i.e., points B as shown in Figures 5 and 6.

Figure 5 Comparison of oxygen consumption rates of 1# coal sample experimental result and proposed theoretical model at the critical temperature (Tc)
Comparisons between oxygen consumption rates of experimental result and theoretical model are represented in Figures 5 and 6. For 1# coal sample, oxygen consumption rate calculated by our proposed theoretical model is approximately 0.138 mol/(m3·s), which is remarkably close to the rate of oxygen depletion deduced from experimental data (approximately 0.132 mol/(m3·s)). Similar result can be observed from Figure 6. Theoretical oxygen depletion rate is 0.138 mol/(m3·s), which is merely 11% faster than that obtained from laboratory-scale experiment (0.124 mol/(m3·s)). Comparisons between theoretical and experimental results indicate that our proposed theoretical model to estimate oxygen consumption rate at high temperature is in line well with laboratory-scale experimental results, which validates our proposed approach. The rate of oxygen consumption is slightly higher than that deduced from experimental data, which may be contributed to accuracy of curve fitting method, heterogeneity of coal samples and limitations of the programmable isothermal oven experiments.

Figure 6 Comparison of oxygen consumption rates of 2# coal sample experimental result and proposed theoretical model at the critical temperature (Tc)
As shown in Figures 5 and 6, oxygen consumption rate is controlled by kinetic reaction and increases rapidly when coal samples’ temperature is lower than the critical temperature (Tc); at the critical temperature (Tc) oxygen consumption rate starts to be controlled by oxygen transport and will level off when temperature of self-ignition coal outstrips the critical temperature.
In practice, oxygen consumption rate is related not only to temperature and coal properties but also to the ambient air flow and diameter of coal particle [5, 8]. These factors are excluded by conventional methods: Arrhenius equation and curve fitting for experimental data. Additionally, because of different timescales of kinetic reaction and oxygen transport at high temperature, oxygen consumption rate illustrated by these two methods may result in no convergence of simulating high-temperature spontaneous combustion of coal or coal fires. Although the Operator-Split (OS) method can successfully solve this issue [23, 25, 26], it is difficult to feasibly incorporate it into packed simulation codes. Our proposed formulation of oxygen depletion rate seems more reasonable because it involves more factors: coal properties, temperature, ambient flow (Pr, Re, and D) and diameter of coal particle (d). A variety of research found that oxidation rate is proportional to power exponent of diameter of coal particle (r~ d–n, where n is an exponent quantifying the dependence of the oxidation rate on grain size) [5, 8], which is roughly represented in our model. Furthermore, at high temperature simulations of self-ignition is much easier to be convergent using our proposed formula of oxygen consumption rate because paradoxical situation of different timescales of oxygen consumption and oxygen transport is solved. Therefore, it can be feasibly incorporated into packed CFD codes to simulate high-temperature stage of self-ignition or coal fires, but not low-temperature self-heating.
5 Conclusions
1) Oxygen consumption rate of spontaneous combustion of coal exponentially increases with temperature. In practice, oxygen consumption rate is associated not only with coal properties and temperature but also with the ambient air flow and diameter of coal particle. At high temperature, oxygen consumption rate is controlled by oxygen transport when oxygen consumption rate of kinetic reaction is faster than oxygen transport rate because oxidation reaction will merely proceed as long as sufficient fresh oxygen is transported to self- ignition coal.
2) Based on heat and mass transfer in porous coal, Arrhenius equation and the Ranz-Marshall correlation, a theoretical equation of oxygen consumption rate at high temperature was proposed. This theoretical equation involves coal properties, temperature, the ambient air flow characteristics and diameter of coal particle, which is more reasonable to present the actual rate of oxygen depletion.
3) The programmable isothermal oven experiment was adopted to validate our proposed model. The rates of oxygen consumption obtained from experiments and calculated by our proposed model were compared, which suggests that oxygen consumption rates calculated by our theoretical model agree well with those deduced from laboratory-scale experiments and further validates our proposed model.
4) The novel formula of oxygen consumption rate is more effective than conventional approaches because it involves more factors affecting oxygen consumption and solves the convergent issue caused by different timescales of oxygen consumption and oxygen transport. Therefore, it can be feasibly and effectively utilized to simulate of high-temperature stage of spontaneous combustion of coal or coal fires, but not low-temperature self-heating.
References
[1] YANG Fu-qiang, WU Chao, LI Zi-jun. Spontaneous combustion tendency of fresh and pre-oxidized sulfide ores [J]. Journal of Central South University, 2014, 21(2): 715–719.
[2] YANG Fu-qiang, WU Chao. Mechanism of mechanical activation for spontaneous combustion of sulfide minerals [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(1): 276–282.
[3] ZHANG Jiang-zhong, KUENZER C. Thermal surface characteristics of coal fires 1: Results of in-situ measurements [J]. Journal of Applied Geophysics, 2007, 63(3): 117–134.
[4] ZHU Hong-qing, SONG Ze-yang, TAN Bo, HAO Yu-ze. Numerical investigation and theoretical prediction of self-ignition characteristics of coarse coal stockpiles [J]. Journal of Loss Prevention in the Process Industries, 2013, 26(1): 236–244.
[5] TARABA B, MICHALEC Z. Effect of longwall face advance rate on spontaneous heating process in the gob area—CFD modelling [J]. Fuel, 2011, 90(8): 2790–2797.
[6] YUAN Li-ming, SMITH A C. The effect of ventilation on spontaneous heating of coal [J]. Journal of Loss Prevention in the Process Industries, 2012, 25(1): 131–137.
[7] QIN Yue-ping, LIU Wei, YANG Chun, FAN Zheng-zhong, WANG Liang-liang, JIA Guo-wei. Experimental study on oxygen consumption rate of residual coal in goaf [J]. Safety Science, 2012, 50(4): 787–791.
[8] YUAN Li-ming, SMITH A C. Numerical study on effects of coal properties on spontaneous heating in longwall gob areas [J]. Fuel, 2008, 87(15): 3409–3419.
[9] AKGUN F, ESSENHIGH R H. Self-ignition characteristics of coal stockpiles: Theoretical prediction from a two- dimensional unsteady-state model [J]. Fuel, 2001, 80(3): 409–415.
[10] EJLALI A, AMINOSSADATI S M, HOOMAN K, BEAMISH B B. A new criterion to design reactive coal stockpiles [J]. International Communications in Heat and Mass Transfer, 2009, 36(7): 669–673.
[11] EJLALI A, MEE D J, HOOMAN K, BEAMISH B B. Numerical modelling of the self-heating process of a wet porous medium [J]. International Journal of Heat and Mass Transfer, 2011, 54(25): 5201–5206.
[12] KRISHNASWAMY S, AGARWAL P K, GUNN R D. Low-temperature oxidation of coal 3. Modelling spontaneous combustion in coal stockpiles [J]. Fuel, 1996, 75(3): 353–362.
[13] KUENZER C, STRACHER G B. Geomorphology of coal seam fires [J]. Geomorphology, 2012, 138(1): 209–222.
[14] STRACHER G B. Coal fires burning around the world: A global catastrophe [J]. International Journal of Coal Geology, 2004, 59(1, 2): 1–6.
[15] WU Jian-jun, LIU Xiao-chen. Risk assessment of underground coal fire development at regional scale [J]. International Journal of Coal Geology, 2011, 86(1): 87–94.
[16] VAN D P, ZHANG Jian-zhong, JUN Wang, KUENZER C, WOLF Karl-Heinz. Assessment of the contribution of in-situ combustion of coal to greenhouse gas emission; based on a comparison of Chinese mining information to previous remote sensing estimates [J]. International Journal of Coal Geology, 2011, 86(1): 108–119.
[17] ROSEMA A, GUAN H, VELD H. Simulation of spontaneous combustion, to study the causes of coal fires in the Rujigou basin [J]. Fuel, 2001, 80(1): 7–16.
[18] ZHU Jian-fang, HE Ning, LI Deng-ji. The relationship between oxygen consumption rate and temperature during coal spontaneous combustion [J]. Safety Science, 2012, 50(4): 842–845.
[19] BEAMISH B B, BARAKAT M A, GEORGE J D S. Adiabatic testing procedures for determining the self-heating propensity of coal and sample ageing effects [J]. Thermochimica Acta, 2000, 362(1, 2): 79–87.
[20] BEAMISH B B, BLAZAK D G. Relationship between ash content and R70 self-heating rate of callide coal [J]. International Journal of Coal Geology, 2005, 64(1, 2): 126–132.
[21] HE Qi-lin, WANG De-ming. Comprehensive study on the rule of spontaneous combustion coal in oxidation process by TG-DTA-FTIR technology [J]. Journal of China Coal Society, 2005, 30(1): 53–57. (in Chinese)
[22] KRAJ IOV M, JELEMENSK L, KI
IOV M, JELEMENSK L, KI A M, MARKO
A M, MARKO J. Model predictions on self-heating and prevention of stockpiled coals [J]. Journal of Loss Prevention in the Process Industries, 2004, 17(3): 205–216.
J. Model predictions on self-heating and prevention of stockpiled coals [J]. Journal of Loss Prevention in the Process Industries, 2004, 17(3): 205–216.
[23] WESSLING S, KESSELS W, SCHMIDT M, KRAUSE U. Investigating dynamic underground coal fires by means of numerical simulation [J]. Geophysical Journal International, 2008, 172(1): 439–454.
[24] FU Wei-biao. The macro-general rules of coal combustion theories [M]. Beijing: Tsinghua University Press, 2003. (in Chinese)
[25] CHERTOCK A, KURGANOV A, PETROVA G. Fast explicit operator splitting method for convection–diffusion equations [J]. International Journal for Numerical Methods in Fluids, 2009, 59(3): 309–332.
[26] DUARTE M, DESCOMBES S P, TENAUD C, CANDEL S B, MASSOT M. Time–space adaptive numerical methods for the simulation of combustion fronts [J]. Combustion and Flame, 2013, 160(6): 1083–1101.
(Edited by HE Yun-bin)
中文导读
一种计算煤自燃耗氧速率的新方法
摘要:根据煤自燃的热量传导和传质特性、阿伦尼乌兹公式和Ranz-Marshall方程, 提出了一种估算煤在高温自燃耗氧速率的新方法。与传统方法相比,该方法不仅考虑了煤的自燃动力学特性和温度, 还包含了煤粉的环境气流特性和粒径,并通过煤自燃程序升温实验与理论结果的对比,表明该方法计算的氧耗速率与实验结果一致,验证了该方法的有效性。
关键词:煤自燃;耗氧速率;供氧;时间尺度分析;临界温度;煤自燃程序升温实验
Foundation item: Project(51534008) supported by the National Natural Science Foundation of China
Received date: 2017-03-27; Accepted date: 2018-03-09
Corresponding author: SONG Ze-yang, PhD; Tel: +86-18500121577; E-mail: eagle0721@sohu.com; ORCID: 0000-0001-6326-5207
Abstract: Based on heat and mass transfer characteristics of spontaneous combustion of coal, Arrhenius equation and the Ranz-Marshall correlation, a novel approach was proposed in this paper to estimate oxygen consumption rate of self-ignition of coal at high temperature. Compared with the conventional methods, this approach involves not only kinetic properties of self-ignition of coal and temperature, but also the ambient air flow characteristics and diameter of coal particle. To testify the proposed approach, oxygen consumption rates at high temperature were measured by the programmable isothermal oven experiments. Comparisons between experimental and theoretical results indicate that the rates of oxygen depletion calculated by the proposed approach agree well with those measured from laboratory-scale experiments, which further validates the proposed approach.


