J. Cent. South Univ. (2012) 19: 2584-2590
DOI: 10.1007/s11771-012-1314-9![]()
Parametric optimization and performance comparison of organic Rankine cycle with simulated annealing algorithm
WANG Zhi-qi(王志奇)1,2, ZHOU Nai-jun(周乃君)1, ZHANG Jia-qi(张家奇)1,
GUO Jin(郭静)1, WANG Xiao-yuan(王晓元)1
1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;
2. Institute of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract:
Taking the ratio of heat transfer area to net power and heat recovery efficiency into account, a multi-objective mathematical model was developed for organic Rankine cycle (ORC). Working fluids considered were R123, R134a, R141b, R227ea and R245fa. Under the given conditions, the parameters including evaporating and condensing pressures, working fluid and cooling water velocities were optimized by simulated annealing algorithm. The results show that the optimal evaporating pressure increases with the heat source temperature increasing. Compared with other working fluids, R123 is the best choice for the temperature range of 100-180 ℃ and R141b shows better performance when the temperature is higher than 180 ℃. Economic characteristic of system decreases rapidly with the decrease of heat source temperature. ORC system is uneconomical for the heat source temperature lower than 100 ℃.
Key words:
1 Introduction
With the fast development of industry, energy shortage and blackouts have appeared more and more frequently all over the world. In this context, using renewable energy like solar energy, wind energy as well as waste heat for electricity production became important. There were abundant waste heat resources available in the process of industry. However, the low-temperature waste heat resources with temperatures of typically below 220 ℃ were discharged. The organic Rankine cycle (ORC) was a promising technique for conversion of low-temperature heat to power [1].
Much research has been conducted on the ORC system. MAGO et al [2] indicated that R113 exhibited best thermal efficiency while iso-butane showed the worst efficiency. SALEH et al [3] found the highest thermal efficiency was 0.13 for the high boiling substances in sub-critical processes with n-butane. LAKEW and BOLLAND [4] found that R227ea gave the highest power for heat source temperature range of 80-160 ℃ and R245fa produced the highest power in the range of 160-200 ℃. Although these researches found the suitable working fluid for the ORC, they did not evaluate the ORC performance under the optimization condition.
MADHAWA et al [5] used the ratio of the total heat exchanger area to net power output as the objective function and it was optimized using the steepest descent method. The results showed that the objective function value between different working fluids could be more than two-fold. DAI et al [6] optimized thermodynamic parameters of the ORC with exergy efficiency as an objective function. And some researchers made the maximum thermal efficiency and net power as the optimization criteria [7-8]. They observed that the choice of working fluid could greatly affect the system performance. However, these researches did not take the heat recovery efficiency and the cost of total system into account. Besides, the optimization algorithm in most documents was the traditional method and easy to converge to sub-optimal solutions in the process of searching for the optimum.
Compared with the traditional algorithms, simulated annealing algorithm had many advantages in simple description, flexible usage, running efficiency and less restriction in initial conditions. As a result, a lot of applications have been found in various engineering fields [9-10]. The parameters were optimized by simulated annealing algorithm and the system cost was investigated in this work. The objective function considered was not only the ratio of heat exchanger area to net power but also waste heat recovery efficiency. The main objective of this work was focused on finding the optimal parameters and a suitable working fluid for ORC system.
2 Mathematical model
2.1 Thermodynamic model
The system considered is a simple cycle, which consists of a pump, evaporator, turbine and condenser. The schematic diagram of the ORC system and T-S diagram of the cycle are shown in Fig. 1.
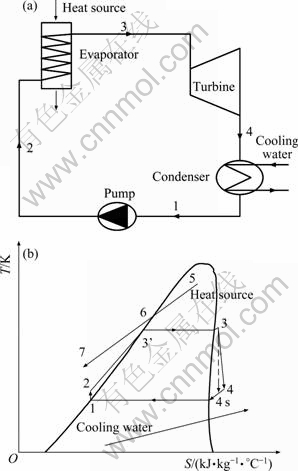
Fig. 1 Sketch of ORC system (a) and T-S diagram (b)
The net power of ORC system is defined as
![]() (1)
(1)
The work done by the turbine can be expressed as
![]() (2)
(2)
where mf is mass flow rate of working fluid, kg/s; h is the specific enthalpy, kJ/kg; 3 and 4 are the state points in Fig. 1.
The consumed powers by working fluid pump and water pump are determined by
![]() (3)
(3)
![]() (4)
(4)
where ρf and ρw are the densities of working fluid and water, respectively, kg/m3; ηp is the efficiency of pump, %; mw is the mass flow rate of water, kg/s; p1 and p2 are the pressures at the state points in Fig. 1, Pa.
The pressure drop in the tube can be given as
![]() (5)
(5)
where λ is the friction factor; l is the length of tube, m; D is the diameter of tube, m; v is the velocity in tube, m/s.
The heat exchanger area is calculated by
![]() (6)
(6)
![]() (7)
(7)
where K is overall heat transfer coefficient, W/(m2·K); αi is the heat transfer coefficient in tube, W/(m2·K); α0 is the heat transfer coefficient outside, W/(m2·K); ΔT is the temperature difference, ℃; δ is the thickness of tube, m; k is thermal conductivity of tube, W/(m·K); R is the total thermal resistance, W/(m2·K).
Numerical correlations of the heat transfer coefficients between exhaust and evaporator are determined from [11]
![]() (8)
(8)
where Nug, Reg, Prg are the Nusselt number, Reynolds number and Prandlt number of flue gas, respectively.
The Gnielinski equation is used for single-phase working fluid heat transfer [12]:
![]() (9)
(9)
![]() (10)
(10)
A correlation for the convection heat transfer of two-phase flows in a horizontal tube is [13]
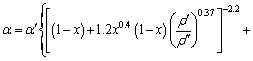
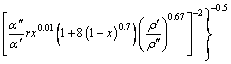 (11)
(11)
where x is the vapor quality, %; the superscripts of ![]() and
and![]() mean saturation liquid and saturation vapor, respectively; r is the latent heat of working fluid, kJ/kg.
mean saturation liquid and saturation vapor, respectively; r is the latent heat of working fluid, kJ/kg.
The condensation heat transfer coefficient is calculated by [14]
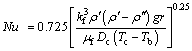 (12)
(12)
where μf is the viscosity of working fluid, Pa·s; Tb and Tc are the wall temperature and temperature of working fluid, respectively, ℃.
The heat recovery efficiency is the ratio of the available energy to the maximum usable energy from waste heat:
![]() (13)
(13)
2.2 Optimization model
1) Objective function
In order to improve the power produced by per unit of heat exchanger area, the ratio of the total heat exchanger area to net power output is selected as the objective function:
![]() (14)
(14)
On the other hand, higher heat availability means more energy recovered from wasted heat. Therefore, the second objective function is the heat recovery efficiency:
![]() (15)
(15)
Based on the two models, the evaluation function for the optimization is expressed by
![]() (16)
(16)
where w1 and w2 are the weighting coefficients for the objective functions of f1(X) and f2(X), respectively.
2) Design variables
The objective functions are closely correlated with the specific enthalpy of working fluid. And the specific enthalpy is closely related with the pressures in evaporator and condenser. Therefore, the pressure is the important parameter which affects the system performance. Besides, the heat transfer coefficient and pressure drop in tube vary with the velocities in evaporator and condenser. Therefore, the evaporating and condensing pressures, working fluids and cooling water velocities are the design variables:
![]() (17)
(17)
3) Constraints
In order to produce new solutions for the annealing algorithm, basic constrained conditions are given according to various demands.
In order to avoid the air coming into condenser, the condensing pressure should be greater than atmospheric pressure. So, x2-0.101≥0. According to the characteristic of ORC system, the evaporation pressure should be higher than the condensing pressure and less than the critical pressure. This means x1-x2>0 and x1
c. And the minimum velocity in tube should be larger than zero. So, x3>0 and x4>0.
2.3 Economic model
In the low-temperature waste heat power plant, the heat exchangers (evaporator and condenser) contribute largely to the total cost. It is reasonable because 80%-90% of the system capital cost is assigned on the heat exchangers [15]. The capital cost of each heat exchanger is determined by the following general correlation [16]:
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
where F1, F2, F3, B1, B2, C1, C2 and C3 are coefficients required for cost evaluation of each equipment and the values are obtained in Ref. [16].
Considering the cost of other system equipment (turbine and pump), there is a coefficient for the total cost of heat exchangers:
![]() (21)
(21)
The cost of power plant is further converted from 1996 costs to 2008 costs by using chemical engineering plant cost index (CEPCI) values:
![]() (22)
(22)
where CI,1996=382 and CI,2008=575.4.
The capital recovery cost (CRF) is estimated based on the following relation:
![]() (23)
(23)
where i is the interest rate and set as 6%, and Ts is the plant life time and set as 20 a.
Electricity production cost can be calculated by
![]() (24)
(24)
where Cs is the operation and management cost of the system, which is 1.5% of the total cost. Os is the operation time of the plant and set as 7 500 h.
The payback period of system is determined by
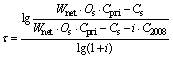 (25)
(25)
where Cpri is the price of electricity and it is set to 0.5 RMB Yuan/(kW·h).
3 Simulated annealing algorithm for optimization
The simulated annealing algorithm is originated from the simulation of solid annealing process, such as growing silicon in the form of highly ordered, defect-free crystals. In order to accomplish this, the material is annealed. It is first heated to a temperature that permits many molecules to move freely with respect to each other. Then, it is cooled carefully and slowly until the material freezes into a crystal, which is completely ordered and thus the system is at the state of minimum energy.
In the optimum searching process, the objective function to a certain optimization problem is regarded as an equivalence of the energy and the value of control parameter t which is reduced gradually and regarded as the temperature in solid annealing process. For each value of control parameter, the algorithm continues the iterative process to generate new solutions, judge it, then accept or abandon it, which corresponds to the heat balance process in a constant solid temperature. As the process is repeated and t tends to zero, the global optimal solution is obtained.
The main idea of this algorithm is to first produce a series of relative optimization solutions by Metropolis algorithm, and continue the iterative process by the criterion of Metropolis, which decides whether to accept the transition from current solution i to a new solution j according to the transition probability B:
![]() (26)
(26)
Therefore, the simulated annealing algorithm can be considered as an iterative process of Metropolis algorithm with the decrease of controlling parameter value. The flow chart of the simulation procedure is shown in Fig. 2.
4 Results and discussion
In the simulation, the volume flow rate of heat source is 300 000 m3/h and the temperature of heat source is 140 ℃. The heat exchanger is assumed to be a shell and tube counter-current design. The pinch temperature differences in the evaporator and condenser are assumed to be 10 ℃ and 5 ℃, respectively. The isentropic efficiencies for the turbine and pump are both assumed to be 80%. The working fluid at the exit of the evaporator is saturated vapor. The inlet temperature of the cooling water and the ambient temperature are both set as 20 ℃. The weighting coefficients for objective function are w1=0.6 and w2=0.4, respectively. Five working fluids (R123, R134a, R227ea, R141b and R245fa) are considered in this analysis.
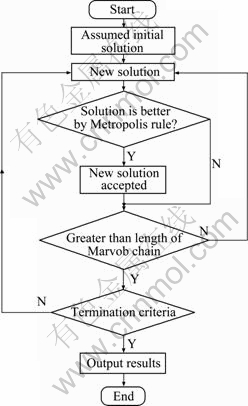
Fig. 2 Procedure of simulated annealing algorithm
4.1 Validation
According to the developed model, the ORC simulation is performed by using a simulation program written in Matlab software. Numerical solution is validated with the results of LIU et al [17] for the ideal Rankine cycle using HCFC 123 as the working fluid and in the same operating conditions. During the validation, waste heat temperature is 200 ℃ and condenser temperature is 30 ℃.
The comparison shows very good agreement between present solution and the results of LIU et al [17]. as shown in Fig. 3. This accuracy is believed to be sufficient for most engineering applications.
4.2 Results and analysis
The effects of variables on the value of objective function for R123 are shown in Figs. 4 and 5.
As shown in Fig. 4, the objective function value of R123 in ORC reaches a minimum for specific values of evaporating and condensing pressures. The optimal evaporating and condensing pressures are 0.692 MPa and 0.109 MPa, respectively. The reason is that with the increase of pressure difference between evaporator and condenser, the enthalpy difference in turbine increases. This leads to more net power output. When the evaporating pressure is too large, the temperature difference between working fluid and heat source decreases rapidly. This results in a rapid increase of heat exchanger area.
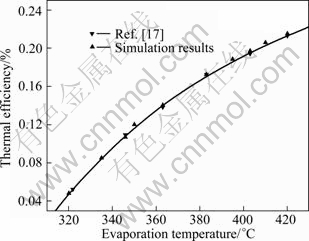
Fig. 3 Comparison of numerical results
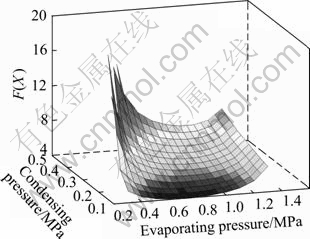
Fig. 4 Variation of F(X) with condensing pressure and evaporating pressure for R123
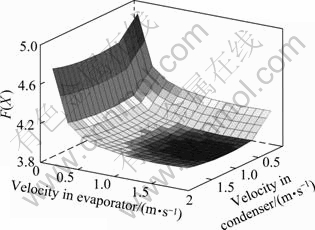
Fig. 5 Variation of F(X) with velocity in evaporator and condenser for R123
Figure 5 shows that the value of objective function increases with the decrease of velocity in evaporator and condenser. This is because heat transfer coefficient in heat exchanger decreases with the velocities, which leads to the increase of heat exchange area. However, the pressure drop in system and power consumed by pumps increases with the velocity in tube. Therefore, the high velocity in the tube will reduce the net power of system. The optimal velocities for evaporator and condenser are 0.85 m/s and 1.45 m/s, respectively.
Under the optimal operation conditions, the results for different working fluids are given in Table 1.
According to Table 1, the performance difference between different working fluids is large. Compared with other working fluids, the objective function value for R123 is the lowest, followed by R245fa and R141b. The R134a and R227ea show the largest objective function value. The trend for the ratio of heat exchanger area to net power output is similar to the objective function. For R123, the ratio of total heat exchanger area to net power output is 5.48 m2/kW. Compared with R134a, it decreases by 36.8%.
Under the optimal parameters, value of evaluation function and heat availability as a function of heat source temperature is plotted in Figs. 6 and 7.
Figure 6 shows that as the heat source temperature increases, the objective function value decreases for R141b. However, objective function values for R123, R245fa, R227ea and R134a decrease first and then increase at a special temperature. At last, they decrease with the increase of heat source temperature. From Fig. 7, it can be seen that the heat availability efficiency increases with the heat source temperature. This means that more heat is transferred from waste heat to evaporator and the average temperature difference between them becomes less. When the heat recovery efficiency closes to the maximum (1.0), the average temperature difference reaches the minimum. This results in the rapid increase of heat exchanger area of evaporator. Although the net power output increases with heat availability efficiency, the percentage of increase for net power is lower than the percentage of increase for heat exchanger area. Therefore, the objective function increases rapidly at special temperature. For R227ea, R134a and R245fa, the corresponding temperatures of objective function value increasing suddenly are 140, 200 and 220 ℃, respectively. This is consistent with the normal boiling temperature. For R245fa, the objective function value is 3.1 at 180 ℃ and it increases to 3.8 at 200 ℃. This means that higher heat source temperature does not result in better performance.
Table 1 Performance comparison of fluids under optimal operation parameters
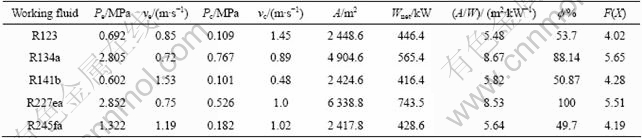
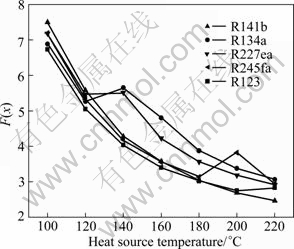
Fig. 6 Objective function for different heat source temperature in optimum condition
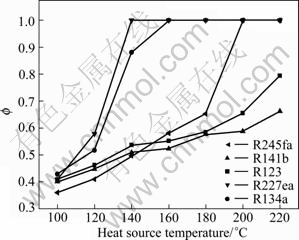
Fig. 7 Heat availability for different heat source temperature in optimum condition
The function value of R227ea at 140 ℃ increases by 36.6% compared with R123. This indicates that selection of the suitable working fluid according to the heat source temperature is very important for ORC system. It is obvious that when the heat source temperature ranges from 100 to 180 ℃, the objective function value of R123 is the lowest. So, R123 is the best choice for the heat source with temperature below 180℃. And R141b is the optimal working fluid when the temperature is higher than 180 ℃.
The economic analysis for the ORC system under the optimal conditions is plotted in Fig. 8.
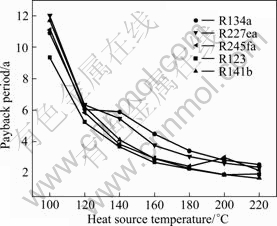
Fig. 8 Payback period for different heat source temperatures
Figure 8 shows that when the heat source temperature is 140 ℃, the payback period for R123 is 3.68 a. Compared with R123, the payback period of R134a increases by 59.8%. It is observed that the choice of working fluid can greatly affect the power plant cost. When the heat source temperature is below 180 ℃, R123 shows the best economic performance. And when the temperature is higher than 180 ℃, R141b has better economy.
The payback period is closely correlated with the ratio of heat exchanger area to net power. As a result, the trend of economic performance with the heat source temperature is similar to the evaluation function. It can be seen from Fig. 8 that the heat source temperature is an important factor on payback period. When the temperature is 120 ℃, the payback period of R123 is 5.25 a. This shows that the economy performance for ORC system under this temperature is good. However, the payback period increases by 76.6% when the heat source temperature decreases to 100 ℃. The payback period reaches 9.35 a and it is too long for the ORC system. Therefore, the ORC system is unsuitable to the heat source with temperature below 100 ℃.
5 Conclusions
1) Higher heat source temperature does not mean better performance for the same pinch temperature difference.
2) There exists optimum combination of parameters minimizing the ratio of heat exchanger area to net power and maximizing the heat availability values. The optimal evaporating pressure increases with the heat source temperature.
3) Compared with other working fluids, R123 is the optimal working fluid for the temperature below 180 ℃, and R141b shows better performance when the temperature is higher than 180 ℃.
4) The ORC system is uneconomical for the heat source temperature lower than 100 ℃.
References
[1] SCHUSTER A, KARELLAS S, KAKARAS E, SPLIETHOFF H. Energetic and economic investigation of organic Rankine cycle applications[J]. Applied Thermal Engineering, 2008, 31(8): 1-37.
[2] MAGO P J, CHAMRA L M, SRINIVASAN K, SOMAYAJI C. An examination of regenerative organic Rankine cycles using dry fluids [J]. Applied Thermal Engineering, 2008, 28(8): 998-1007.
[3] SALEH B, KOGLBAUER G, WENDLAND M, FISCHER J. Working fluids for low-temperature organic Rankine cycles [J]. Energy, 2007, 32(7): 1210-1221.
[4] LAKEW A A, BOLLAND O. Working fluids for low-temperature heat source [J]. Applied Thermal Engineering, 2010, 30 (10): 1262-1268.
[5] MADHAWA HETTIARACHCHI H D, MIHAJLO G, WILLIAM M W, YASUYUKI I. Optimum design criteria for an organic Rankine cycle using low-temperature geothermal heat sources [J]. Energy, 2007, 32(9): 1698-1706.
[6] DAI Yi-ping, WANG Jiang-feng, GAO Lin, Parametric optimization and comparative study of organic Rankine cycle (ORC) for low grade waste heat recovery [J]. Energy Conversion and Management, 2009, 50(3): 576-582.
[7] SCHUSTER A, KARELLAS S, AUMANN R. Efficiency optimization potential in supercritical organic Rankine cycles [J]. Energy, 2010, 35(2): 1033-1039.
[8] ROY J P, MISHRA M K, MISRA A. Parametric optimization and performance analysis of a waste heat recovery system using organic Rankine cycle [J]. Energy, 2010, 35(12): 5049-5062.
[9] ZOU En, LI Xiang-fei, LIU Ou-geng, ZHANG Tai-shan. Optimization design for parameters of FNN: Learning algorithm of chaos simulated annealing [J]. Journal of Central South University: Science and Technology, 2004, 35(3): 443-447. (in Chinese)
[10] ZHOU Long, MOU Yi, YOU Xin-ge. Application of simulated annealing algorithm in image segmentation of pests in stored grain [J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2010, 38(5): 72-74. (in Chinese)
[11] YANG Shi-ming, TAO Wen-quan. Heat trans-fer [M]. Shanxi: Northwest Industrial University Press, 2006: 177. (in Chinese)
[12] WEI Dong-hong, Lu Xue-sheng, LU Zheng, GU Jian-ming. Dynamic modeling and simulation of an organic Rankine cycle (ORC) system for waste heat recovery [J]. Applied Thermal Engineering, 2008, 28(10): 1216-1224.
[13] JENSEN J M. Dynamic modeling of thermo-fluid systems with focus on evaporators for refrigeration [D]. Denmark: Department of Mechanical Engineering, Technical University of Denmark, 2003.
[14] QIAN Song-wen. Heat exchanger design handbook [M]. Beijing: Chemical Industry Press, 2002: 68. (in Chinese)
[15] PAPADOPOULOS A I, STIJEPOVIC M, LINKE P. On the systematic design and selection of optimal working fluids for organic Rankine cycle [J]. Applied Thermal Engineering, 2010, 30(6): 760-769.
[16] ZHANG Sheng-jun, WANG Huai-xin, GUO Tao. Performance comparison and parametric optimization of sub-critical organic Rankine cycle (ORC) and trans-critical power cycle system for low-temperature geothermal power generation [J]. Applied Energy, 2011, 88(8): 2740-2754.
[17] LIU B T, CHIEN K H, WANG C C. Effect of working fluids on organic Rankine cycle for waste heat recovery [J]. Energy, 2004, 29 (8): 1207-1217.
(Edited by YANG Bing)
Foundation item: Project(2009GK2009) supported by Science and Technology Department Funds of Hunan Province, China; Project(08C26224302178) supported by Innovation Fund for Technology Based Firms of China
Received date: 2011-07-11; Accepted date: 2011-09-27
Corresponding author: WANG Zhi-qi, PhD Candidate. Tel: +86-13789306990; E-mail: wangzhiqi@xtu.edu.cn
Abstract: Taking the ratio of heat transfer area to net power and heat recovery efficiency into account, a multi-objective mathematical model was developed for organic Rankine cycle (ORC). Working fluids considered were R123, R134a, R141b, R227ea and R245fa. Under the given conditions, the parameters including evaporating and condensing pressures, working fluid and cooling water velocities were optimized by simulated annealing algorithm. The results show that the optimal evaporating pressure increases with the heat source temperature increasing. Compared with other working fluids, R123 is the best choice for the temperature range of 100-180 ℃ and R141b shows better performance when the temperature is higher than 180 ℃. Economic characteristic of system decreases rapidly with the decrease of heat source temperature. ORC system is uneconomical for the heat source temperature lower than 100 ℃.


