Article ID: 1003-6326(2005)05-1049-06
Numerical modeling of damping capacity of Zn-Al alloys with fully lamellar microstructures
WANG Jin-cheng(王锦程)1, ZHANG Zhong-ming(张忠明)2, YANG Gen-cang(杨根仓)1
(1. State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi'an 710072, China;
2. Department of Materials Science and Engineering, Xi'an University of Technology, Xi'an 710048, China)
Abstract:
The damping behaviors of Zn-Al alloys with fully lamellar microstructures were simulated with the cell method. The influences of the grain boundary condition, the strain amplitude, the number of the lamellae in the grain (N) and the content ratio of Zn and Al in Zn-Al alloys on the damping capacity were investigated. The results indicate that the grain boundary condition has great influence on the damping capacity of Zn-Al alloys, and also affects the relationship between the damping capacity and the number of lamellae (N). The variation of damping capacity with the strain amplitude is increasing exponentially with the strain amplitude and the damping capacity increases with the increasing of content of Zn.
Key words:
damping capacity; Zn-Al alloys; lamellar microstructures; cell method; numerical modeling CLC number: TB331;
Document code: A
1 INTRODUCTION
The performance of structures, such as aerospace, submarine, and machinery in general, can be severely affected by vibrations and noise[1, 2]. Several approaches are used to control noise and vibration, one of which is to manufacture structural and moving components from high-damping alloys[2]. It has been known for some time that certain zinc-aluminum alloys fall into the category of high damping alloys within certain ranges of temperature and vibration frequency[3]. As a kind of high damping alloy, Zn-Al alloys have been investigated first by Nowick[4], who studied the relationship of the precipitated phase and the internal friction of the Al-39.3%Zn. Nutull[5] also investigated the damping behaviors of the superplastic Zn-22%Al alloys. These works are the fundamental researches, which have promoted the development of Zn-Al high damping alloys to a great extent. From the early 1980s, the damping behaviors of Zn-Al alloys have been investigated extensively[6-11]. When we review on the investigations on the Zn-Al high damping alloys over the past 20 years, we can know they mainly can be subdivided into two aspects: one is about the damping mechanisms, such as the formation of the internal friction peak, the contribution of different interface on the damping capacity, etc; the other is about the preparation technologies for the high damping alloys, including alloying, heat treatment and extruding.
However, there still exist plenty of problems to be solved, especially in the relationship between the microstructures and the damping capacity. Lamellar microstructure is one of the most important characteristics for Zn-Al alloys, which is always the product of eutectoid reaction. This lamellar microstructure has a so strong relation with the mechanical properties, including the damping capacity that it is quite necessary to have a deep understanding of how the lamellar structure influences the damping capacity. However, this question is still in debate, the reason for which may come from the difficulties of preparing fully, regular lamellar microstructure. This makes it very hard to find the controlling factor from the complex, irregular microstructures. Despite the conventional method in investigation—through lots of experiments—has made a great contribution to the development of materials science, sometimes, experimental method does not take effect.
With the development of the computational materials science, materials scientists eventually find that the problems which are difficult to solve by experiments method may sometimes be easily accomplished by numerical method. These should be ascribed to the advantage of numerical method which can optionally design the microstructures of the alloy as what you want. The relevance of materials modeling is fundamentally predicted on the belief that such analysis and prediction will bring about better understanding and control of materials microstructures, which in turn are essential in the application area of processing, performance evaluation, and ultimately the design of new materials. Chakraborty and Earthmany[12, 13] had investigated the creep behavior of Ti-Al alloys with fully lamel-lar microstructures by finite element method(FEM). The investigation indicates the possibility of simulating the damping behavior of Zn-Al alloy with fully lamellar microstructure by numerical method. Also in applications it is more valuable to investigate the damping behavior at room temperature than that at high temperature since the high damping alloys are mostly used at room temperature. Therefore, in the present paper, the damping behavior of Zn-Al alloys with fully lamellar microstructure at room temperature will be investigated by cell method, together with FEM, especially on the relationship of the lamellar spacing with the damping capacity. The details of the principle of the damping capacity calculation can be found in some of our other papers[14-16].
2 MODEL
2.1 Cell model
The lamellar microstructures of Zn-Al alloys are composed of randomly distributed colonies. Every colony is actually a grain. In the grain, the α phase and η phase are laminated as very tiny lamellar microstructure and maintain nearly the same orientation. However, the orientation of the lamellar for different grains is different, which may result in the isotropic macroscopic properties of the Zn-Al alloys.
Fig.1 shows the cell model of hexagon grains. It is assumed that the Zn-Al alloys are composed of regular hexagon grains. The cell is composed of one full grain and six half grains. The load is applied on the plane of 
along direction Y, which is characterized by strain amplitude. R is the circumradius of the hexagonal equiaxed grain. The other three planes (
, x=1.5R, x=-1.5R) are applied periodical boundary condition. The loading process is quasi-static because now we focus on elastic-plastic deformation. In order to investigate the influence of the lamellar structure on the damping capacity, the lamellar microstructure model of Zn-Al alloy is shown in Fig.2. In the model, it is assumed that the microstructure of Zn-Al alloys is composed of regular hexagonal equiaxed grains. In each grain, the α phase and η phase form lamellas as shown in Fig.2. The lamella thickness of the α phase and η phase are dA and dB, respectively. The lamellar spacing d=dA+dB. The number of the lamellae in each grain 
. So the different lamellar spacing is obtained by adjusting the lamellae number of N.
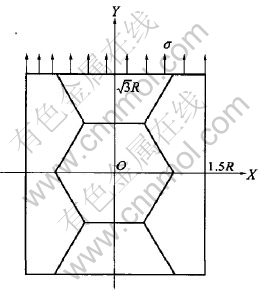
Fig.1 Sketch of cell of hexagon grain of Zn-Al alloy
Fig.2 Schematic illustration of model of lamellar microstructure of Zn-Al alloy
According to the above cell model, the damping capacity of Zn-Al alloy with fully lamellar microstructure can be numerically simulated by the cell method. Fig.3(a) shows the cell and Fig.3(b) is the grid meshing. In Fig.3, the parts with different grey degree indicate the two phases α and η. The orientation of lamellae varies in different grains. The 8-nodes quadrilateral generalized plane strain elements are used. It is assumed that the interface between the lamellar is an ideal interface so that the calculation is simplified. But the grain boundary is investigated in several cases, ideal and imperfect (weak) by contact element method. And also, the details can be found in some of our other papers[17, 18].
Fig.3 Illustration of cell of lamellar microstructure in Zn-Al alloy(a) and its grid meshing(b)
2.2 Materials parameters
The mechanical properties of α phase and η phase are very difficult to measure. But from the equilibrium phase diagram, we know that the solid solubility of both α phase and η phase in Al and Zn respectively are more than 90%. Therefore, it is reasonable to substitute the mechanical properties of pure Al and Zn for that of α phase and η phase respectively in the calculation.
Both α phase and η phase are assumed to be elasto-plastic and obey the von Mises criterion. When they yield, the isotropic power-hardening model is assumed to be valid and the flow stress is written as
where σ0y is the initial yield stress, h is the coefficient of hardening, ε[DD(-*2]-[DD)]p is von Mises equivalent plastic strain, and n is the power of strain hardening.
The parameters of the α phase and η phase are listed as follows[19, 20]: Eη=96.5GPa, vη=0.3, σ0(η)y=37MPa, hη=23MPa, nη=0.435; Eα=70GPa, vα=0.33, σ0(α)y=250MPa, hα=173MPa, nα=0.455. The subscripts of α and η stand for the α phase and η phase respectively.
3 SIMULATION RESULTS
3.1 Number of lamellae (N)
Fig.4 shows the variation of the damping capacity (ψ) with the number of lamellae (N) in the grain under the condition of ideal grain boundary condition. Fig.4(a) and Fig.4(b) show the cases of different volume fraction of Zn and Al. From the figure, it can be found that under the condition of comparative low strain amplitude (A0), the damping capacity (ψ) of Zn-Al alloys is not sensitive to the variation of N for both case (a) and case (b), while the strain amplitude is high (A0=4.0×10-4), the curve of the damping capacity (ψ) variation with N is concave, that is, with the increasing of N, ψ decreases at first and then increases. From the comparison of Fig.4(a) and Fig.4(b), it can be concluded that the damping capacity is much higher in Fig.4(a) than that in Fig.4(b).
Fig.4 Variation of damping capacity of Zn-Al alloy with N under ideal grain
boundary condition
However, when the grain boundary is weak, not an ideal interface, the situation is quite different, as shown in Fig.5. The variation of the damping capacity of Zn-Al alloys with the number of lamellae in the grain (N) under the condition of weak grain boundary does not monotonously increase or decrease, but increase at first and when reaching the climax it will decrease. The curve is convex and there is a peak in the curves, which means there is an optimum value of N where the damping capacity is the highest. For different strain amplitude, the differences are in the height of the peak. And similar to the situation of ideal grain boundary (Fig.4), the difference between Fig.5(a) and Fig.5(b) are the case of different volume fraction of Zn and Al. The higher volume fraction of Zn leads to the damping capacity in Fig.5(b) being much higher than that in Fig.5(a).
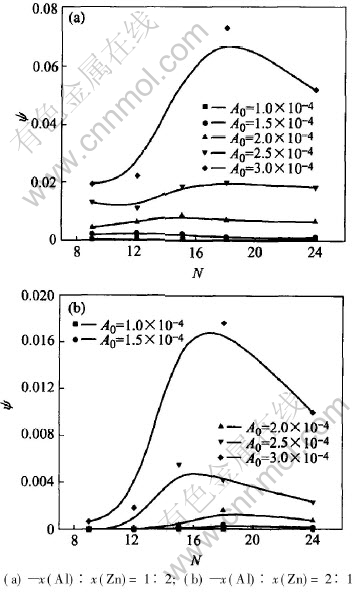
Fig.5 Variation of damping capacity of Zn-Al alloy with N under sliding grain
boundary condition
3.2 Strain amplitude (A0)
Fig.6 shows the influence of the strain amplitude on the damping capacity under different grain boundary conditions and value of N. From the figures, it can be concluded that the variation of damping capacity (ψ) with the strain amplitude (A0) is increasing exponentially with the strain amplitude. And the results also show that the damping capacity of Zn-Al alloys when the grain boundary is ideal, changes little with the different value of N, while when the grain boundary is weak, the damping capacity is different for different value of N.
Fig.6 Influence of strain amplitude on damping capacity of Zn-Al alloy with different N values (x(Al)∶x(Zn)=1∶2)
3.3 Content of Zn
The Zn content also obviously influences the damping capacity of Zn-Al alloys. Fig.7 shows the influence of Zn content on the damping capacity of Zn-Al alloys for different strain amplitude when the grain boundary is weak and the number of the lamellae in the grain is 12. From that it can be found that the damping capacity of the Zn-Al alloy increases with the increasing of content of Zn linearly.
Fig.7 Influence of Zn content on damping capacity of Zn-Al alloy
4 DISCUSSION
Fig.8 shows the illustration of the equivalent plastic strain of the Zn-Al alloys under different grain boundary condition. From Fig.8, it can be found that the maximum of the equivalent plastic strain for the weak grain boundary cell (1.99×10-3) is much higher than that for the ideal grain boundary cell (3.73×10-4). That is to say, when the materials are bearing the same external loading, the material with weak grain boundary has much more micro plastic deformation than that with the ideal grain boundary and the damping capacity is increasing accordingly. As to the influence of the lamellae number in the grain (N) on the damping capacity, it can be explained by the strain compatibility of the materials. When the value of N increases, the lamellar spacing decreases. Because the mechanical properties of the Zn-rich and Al-rich phases are different, the increasing of the interface means increasing the strain un-compatibility. In such cases, the materials are easy to deform, which will lead to much more plastic work. Meanwhile, the decreasing of the lamellae spacing also means the size of the phase decreasing. And to some extent, the decreasing of the phase size will increase the yield strength, which will make the deformation of the materials much more difficult. Therefore, the change of the number of the lamellar in the grain (N) has double effects on the damping capacity, which lead to the variation of the damping capacity with N being not monotonously increasing or decreasing.
As to the variation of the damping capacity with the content of Zn, that is much easier to explain. On one hand, the damping capacity of Zn is much higher than that of Al. So, according to the mixture rule, the damping capacity will increase with the increasing of the content of Zn. On the other hand, with the increasing of the Zn content, the yield strength of the Zn-Al alloys will decrease, which makes the deformation of the materials become much easier and lead to the increasing of the damping capacity.
Fig.8 Illustration of equivalent plastic strain of Zn-Al alloys under different grain boundary conditions
5 CONCLUSIONS
1) Under the condition of ideal grain boundary and high strain amplitude, the damping capacity changes little with the number of the lamellae in the grain (N). However, when the strain amplitude is comparatively low, the damping capacity changes with N markedly. The damping capacity decreases firstly and then increases with the increasing of N.
2) When the grain boundary is a weak interface, the variation curves of the damping capacity with the number of lamellar in the grain (N) are convex, that is, the damping capacity increases with the increasing of N at first, and when it reaches the climax, the damping capacity will decrease with the increasing of N.
3) The variation of damping capacity with the strain amplitude is increasing exponentially with the strain amplitude both for the case of ideal grain boundary and the case of imperfect grain boundary.
4) The damping capacity of Zn-Al alloys for different strain amplitude increases with the increasing of content of Zn.
REFERENCES
[1]Srinivasan A V, Cutts D G, Schetky L M. Thermal and mechanical considerations in using shape memory alloys to control vibrations in flexible structures [J]. Metallurgical Transactions A, 1991, 22A: 623-627.
[2]Zhang J, Perez R J, Wong C R, et al. Effects of secondary phases on the damping behavior of metals, alloys and metal matrix composites [J]. Mater Sci Eng, 1994, R13: 325-390.
[3]Ritchie I G, Pan Z L. High-damping metals and alloys [J]. Metallurgical Transactions A, 1991, 22A: 607-616.
[4]Nowick A S. Anelastic effects arising from precipitation in aluminum-zinc alloys [J]. Journal of Applied Physics, 1951, 22(7): 925-933.
[5]Nuttall K. The damping characteristics of a superplastic Zn-Al eutectoid alloy [J]. Journal of the Institute of Metals, 1971, 99: 266-270.
[6]Batist R D. High damping materials: mechanisms and applications [J]. Journal De Physique, 1983, C9: 39-50.
[7]Kawabe H, Kuwahara K. High damping and modulus characteristics in a superplastic Zn-Al alloy [J]. Journal De Physique, 1981, C5: 941-946.
[8]Schaller R. Metal matrix composites, a smart choice for high damping materials [J]. Journal of Alloys and Compounds, 2003, 355: 131-135.
[9]Lu J S, Aken D C V. Analysis of damping in particle-reinforced super-plastic zinc composites [J]. Metallurgical and Materials Transactions A, 1996, 27A: 2565-2573.
[10]ZHANG Zhong-ming, WANG Jin-cheng, YANG Gen-cang, et al. Microstructural evolution of the supersaturated ZA27 alloy and its damping capacities [J]. Journal of Materials Science, 2000, 35: 3383-88.
[11]Savaskan T, Murphy S. Decomposition of Zn-Al alloys on quench-aging [J]. Materials Science and Technology, 1990, 6: 695-703.
[12]Chakraborty A, Earthman J C. Numerical models of creep and boundary sliding mechanisms in single phase, dual phase and fully laminar titanium aluminide [J]. Metall Mater Trans A, 1997, 28A(4): 979-989.
[13]Chakraborty A, Earthman J C. Numerical models of creep cavitation in single phase, dual phase and fully laminar titanium aluminide [J]. Acta Mater, 1997, 45(11): 4615-4626.
[14]Wang J, Zhang Z, Yang G. The dependence of damping capacity of PMMCs on strain amplitude [J]. Computational Materials Science, 2000, 18: 205-211.
[15]WANG Jin-cheng, YANG Gen-cang. Numerical modeling of the damping capacity of Al/SiC(p) [J]. Metallurgical and Materials Transactions A, 2003, 34A: 1387-1392.
[16]WANG Jin-cheng, YANG Gen-cang. Finite element micromechanical modeling the damping behaviors of PMMCs at room temperature [J]. Materials Science and Engineering A, 2001, 303(1-2): 77-81.
[17]Ross R B. Metallic Materials Specification Handbook [M]. 4th ed. London: Chapman & Hall, 1992.
[18]Nayer A. The Metals Data Book [M]. New York: McGraw-Hill, 1997.
Foundation item: Project(02G53052) supported by the Aeronautics Science Foundation of China
Received date: 2005-01-16; Accepted date: 2005-06-30
Correspondence: WANG Jin-cheng, PhD; Tel: +86-29-88486067; Fax: +86-29-88492374; E-mail: jchwang@nwpu.edu.cn
