J. Cent. South Univ. Technol. (2009) 16: 0320-0325

DOI: 10.1007/s11771-009-0054-y

Identification of complex compliance for regenerator in thermoacoustic resonator system

ZHANG Chun-ping(张春萍)¹, LIU Wei(刘 伟)¹, WU Feng(吴 锋)²,

GUO Fang-zhong(郭方中)¹, ZHANG Xiao-qing(张晓青)¹

 (1. School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan 430074, China;

2. School of Science, Wuhan Institute of Technology, Wuhan 430073, China)

Abstract:

In thermoacoustic system, the characteristic of complex compliance of a regenerator has a great influence on energy stored and dissipation of the whole engine. In order to investigate the performance of regenerators with different matrix geometries and materials coupled with different acoustic systems, an experimental measurement and analysis method was presented. By measuring the resonant frequency, the complex compliance and quality factor of five kinds of matrix were experimentally analyzed respectively in the system of loudspeaker-driven thermoacoustic resonator (TAR) with different lengths. The experimental results show that the real part of complex compliance of the regenerator with pin-array has a maximum value among the measured matrixes and its quality factor is the largest (28.222) with the least dissipation factor of 0.035 4. So the pin-array matrix is testified to behave more excellently on the energy conversion than other matrixes. Compared with other factors the complex compliance of a regenerator contributes more to the performance of a thermoacoustic system.

Key words:

thermoacoustic; regenerator; resonant frequency; complex compliance; quality factor；

1 Introduction

The continuous conversion of heat and sound power without moving parts in a thermoacoustic engine is based on the thermal interaction of acoustic waves with regenerator. And this kind of irreversible heat and momentum (viscosity) exchange happens between the solid walls of matrix of regenerator and the gaseous working fluid. The cycle of thermoacoustic system is a self-oscillation inspired and sustained by thermoacoustic components (including regenerator and stack) in nature [1]. The oscillating flow in regenerator could be reduced to the compression and expansion of working gaseous in the holes of matrix of regenerator. According to the thermodynamics analysis on the boundary layers of matrix of regenerator, the process of thermoacoustic relax happens in the invaded layer of working gaseous and solid walls of matrix, which makes the temperature differences add between regenerator modulated into entropy wave by sound oscillation depending on three nonlinearity factors of flowing viscosity of working gaseous, finite conductive coefficient and convection transportation and results in the increment of volumetric rate of flowing gaseous (?J) finally [2]. In the point of view of network model, the regenerator is comprised of resistance, inductance and compliance. The matrix of regenerator and oscillating working gaseous parcels within will compose a component of energy stored—resonance by properly parameters matching, then in the ideal condition of dissipation less, the oscillation in regenerator can be maintained steadily to produce power. If the power can compensate the dissipation, the regenerator will work at resonant frequency to achieve the highest efficiency of energy conversion.

For the traditional way of designing thermoacoustic engine, the type of regenerator is chosen based on the acoustical properties of porous matrix [3-5] and the coefficient of performance (cop) is used to evaluate the ability of power conversion of regenerator. Little attention is paid to the influences of the compliance characteristic of different matrixes coupled with different systems on the performance of a thermoacoustic engine. Since different combinations of gaseous working fluid and solid material lead to different dissipative degrees of thermal-relaxation [6], and the dissipation aroused mainly by compliance characteristic greatly influences the quality of energy stored and conversion efficiency, the compliance characteristic of matrix of regenerator has to be studied when a thermoacoustic engine is designed.

In the small cavities of matrix for regenerator, the gaseous working fluid is compressed and expanded. As a result there are an additional phase shift between the oscillations of particle velocity and temperature in the acoustic waves and a directional heat flux along the regenerator. The mean temperature T_m changes axially through the regenerator and hence the mean density ρ₀ changing according to ρ₀∝1/T_m becomes a complex variable. Thus, the complex compliance describing the compressibility of gaseous working fluid is related closely with the dissipation in the boundary layer. Two experimental investigations have been developed on complex compliance about different kinds of matrix coupled with different TAR systems for its important role in the whole engine. And the quality factor is then used as the figure of merit of regenerator comprised of matrix to evaluate its influence on the ability of power amplification to make up some limitation of insufficient heat exchange and leak in an engine evaluated by traditional cop [7]. The detailed experimental investigations can be used as a reference for selecting high efficient regenerator when designing a thermoacoustic engine.

2 Identification of complex compliance

2.1 Theory for complex compliance identification

Throughout the analysis on thermoacoustic system, the average field premise proposed by SWIFT has been applied, taking acoustic wave length as the space scale [8]. In the case of thermoacostic resonator (TAR) device working in a higher frequency band, when the dimension of pore in matrix is much smaller than the shortest wave length of the acoustic wave spectrum, the difference between solid walls of matrix and the compressible fluid parcels should be ignored and regarded as a continuum with complex compliance C(f), which becomes a function of resonant frequency f.

The original definition of fluid system compliance is based on the concept of equilibrium density ρ₀ for compressible fluid:

                                    (1)

which  characterizes the relative changing rate of volume dV/V versus pressure dp. When the gaseous working fluid is compressed during the sound wave propagating, the temperature of gas in these cavities will increase and heat the surrounding solid walls. So the thermoacoustic relaxation process must be added to the compliance to become a complex variable.

In the small range of linear relationship of p and V, the complex compliance of Eqn.(1) can be expressed by pressure response:

                            (2)

where  f is the resonant frequency, V(f) is the volume change with time, V₀ is the equilibrium volume of gas, and p(f) is the pressure response.

By using the small perturbation premise, Eqn.(2) can be further expressed by pressure ratio as follows [9]:

                         (3)

where  p₀ is the equilibrium pressure. Substituting Eqn.(3) into the expression of thermoacoustic function  yields [10]:

                     (4)

where γ is the usual ratio of specific heats. And thus:

                              (5)

This is an important dimensionless quantity deciding the performance of a TAR engine. Thus the complex compliance is related to the experimentally measured normalized pressure response p(f) and can be identified experimentally. Furthermore, the friction resistance occurs at the thin boundary layer near the solid wall because of the small distance between channels of matrix of regenerator. The imaginary part of complex compliance together with resistance determines the sound dissipation and attenuation (see Fig.1) and is proportional to the phase of dynamic pressure p and volume V. So the complex compliance is nearly interrelated to time-averaged acoustic power and becomes an important parameter.

Fig.1 Network model of regenerator (R is resistance and C is complex compliance)

For a regenerator, t=2πfτ_v is the dimensionless viscous relaxation-time of sound wave propagating in the heat and viscosity boundary layers between solid walls of matrix. The diffusion or fluctuation process decides the propagating time of sound wave. For t≈0, the process is mainly through fluctuation. For t≈1, the period of sound wave nearly equals the viscosity relaxation-time τ_v and the diffusion of viscosity functions sufficiently. So the relaxation-time in the thermoacoustic engine results in the nonlinear of sound wave and helps the regenerator to be an active source component.

2.2 Modeling for identification experiment

The sound velocity driven by a loudspeaker in a narrow band near resonant frequency can be imagined as a constant, so the resonant frequency can be determined by measuring the acoustic characteristic of resonator. The length of the matrix sample is much shorter than the length of the tube. From the above facts, the real part of complex compliance divided by the adiabatic compliance of gaseous working fluid itself is [11]:

                         (6)

where  C_r is the real part of complex compliance, C₀ is the adiabatic compliance of gaseous working fluid, f_r is the resonant frequency of regenerator, f₀ is the resonant frequency of empty tube, L is the total length from loudspeaker to the end of the resonator, and l is the length of matrix.

The frequency characteristic of regenerator is a coupling response of the inertance of gas parcel and the compliance of matrix. The acoustic wave drives gas flowing in the channels of regenerator and the friction between gas and matrix causes the dissipative resistance. So the dissipation factor d can be identified from measurement of the 3-dB width of the resonant curve Δf and resonant frequency f of empty tube:

                                     (7)

For a resonator with a regenerator, there are three contributions to the dissipation factor d: d₀ from the empty tube, d_C from the imaginary part of the compliance, and d_R from the viscous boundary layer resistance of the regenerator. Thus we have

d=d₀+d_C+d_R                                 (8)

The values of d and d₀ can be identified by measuring the resonant frequency and bandwidth, and d_R by measuring resistance R, thus d_C can be obtained from Eqn.(8). Subsequently, the imaginary part of complex compliance C_i divided by the compliance of gas C₀ is

                      (9)

For a thermoacoustic engine, it is well known that most energy losses occur in the acoustical boundary layer along the solid walls of matrix of regenerator [12]. When an accurate computation of the energy dissipation in the regenerator is needed, it is necessary to take into account the energy losses in the boundary. The viscosity of the gaseous working fluid in the solid boundary and the resistance of the matrix is the main reason of the energy dissipation. Different regenerators with matrixes coupled with the same system will induce different resonant frequencies and present different quality of energy stored [13-14], so the regenerator should have a high quality factor Q to minimize the dissipation of acoustic power into heat. The quality factor Q is defined as [15]:

                                (10)

where  E_st is the energy stored in the resonator, and  is the average rate of energy dissipation. And the quality factor can be identified by the resonant frequency f and the 3-dB width ?f of the resonant curve [16]:

                                    (11)

From Eqn.(7), the quality factor and the dissipation factor are reciprocal each other. So the complex compliance of the regenerator will influence the performance of the whole engine and becomes an important factor worthy of attention.

In present experiment, an equivalent section cylindrical tube was used as a resonator with an internal diameter of 76 mm. Four high sensitive pressure transducers were flush mounted in the wall of the resonator (A-D). Fig.2 gives the schematic diagram of the measurement apparatus. The regenerator was 50 mm in length and had the same internal diameter with the resonator. In order to achieve more knowledge about complex compliance, two experiments were performed. The first experiment was carried out on the glass wool fibers placed in the resonator with different lengths, from 437.5 to 837.5 mm. The tube was filled with nitrogen gas at pressure of 0.8 MPa. The diameter of glass wool fiber was found by taking random samples and measuring the diameter with the help of an electron microscope. The mean value was 9.97 μm. The mass density of the glass wool was ρ_w=2.2 kg/m³, and the mass density of the glass in the fibers was ρ_g=2 550 kg/m³. By tuning up the driving frequency of loudspeaker, different oscillating pressures of four transducers could be collected and analyzed. After confirming the resonant frequency and acquiring the frequency curve, the complex compliance of glass wool and the quality factor could be obtained.

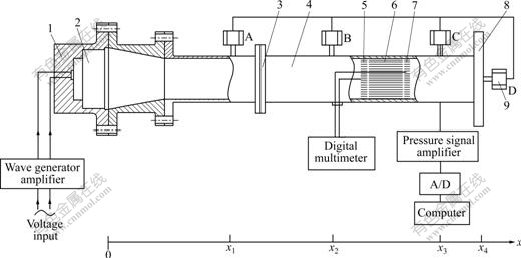
Fig.2 Schematic diagram of measurement apparatus: 1—Acoustic source cavity; 2—Electrodynamic loudspeaker; 3—Flange; 4—Resonator; 5—Cold heat exchanger; 6—Regenerator; 7—Hot heat exchanger; 8—Rigid acoustic termination; 9—Pressure transducer

Fig.3 shows the curves of the theoretically calculated results from Eqn.(3) together with the experimental points of complex compliance from Eqns.(6) and (9) about glass wool. Fig.3(a) shows the real part of the complex compliance of glass wool divided by the compliance of nitrogen. At low frequencies the complex compliance is almost a constant and higher than that at high frequencies. The main reason is that the compression is isothermal at low frequency and adiabatic at high frequency. Fig.3(b) shows the imaginary part of the complex compliance of glass wool divided by the compliance of nitrogen. The curve will have a maximum value at the transition frequency, where the compression goes from isothermal to adiabatic. This point is not shown in Fig.3 because of the finite length of the tube. The quality factor of different resonant frequencies is shown in Fig.4. For L=437.5 mm, the resonant frequency is 250 Hz. Its quality factor of theoretically calculated result is 6.8, while that of the measured result is 6.7. The measured results from Eqn.(11) are little lower than the calculated ones from Eqn.(10) especially at lower frequency, since for the real regenerator, the dissipation of the energy is higher than that of the ideal status.

Fig.3 Measured real part (a) and imaginary part (b) of complex compliance of regenerator at different frequencies

The second experiment was carried out on different matrixes placed in the same resonator. The total length from the loudspeaker to the closed end of the tube was L=637.5 mm. The distances of the transducers to the loudspeaker were 392, 540, 600 and 637.5 mm, respectively. And other parameters for experiment did not change. The regenerator was filled with pin-array, stainless steel filament, glass wool, dense stainless steel screen (aperture of 77 μm and 130 μm) respectively (see Table 1). For the stainless steel filament and glass wool regenerators, measurements had been done twice respectively about the matrix placed parallelly and perpendicularly to the direction of wave propagation in the resonator. The resonant curves of some matrixes are shown in Figs.5-7. The resonant frequencies for pin- array, stainless steel screen (77 μm) and stainless steel filament are 184.32, 181.14 and 181.15 Hz, respectively. Tables 2 and 3 list the measured results of complex compliance and the quality factors of regenerators with different matrixes according to the above experimental method.

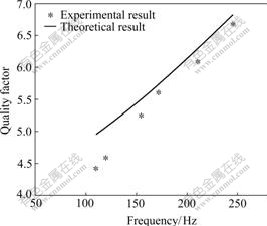
Fig.4 Measured and theoretically calculated results of quality factor at different resonant frequencies for five lengths of tube

Table 1 Parameters of wire and void fraction of matrixes used in the second experiment

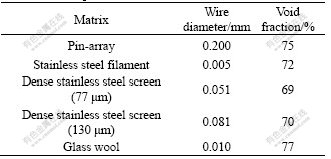
Table 2 Real and imaginary parts of complex compliance of regenerators with different matrixes and their contributions to dissipation factor

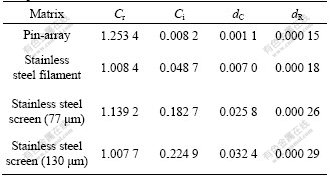
Table 3 Resonant frequency, transmission band, quality factor and dissipation factor of different matrixes of regenerator

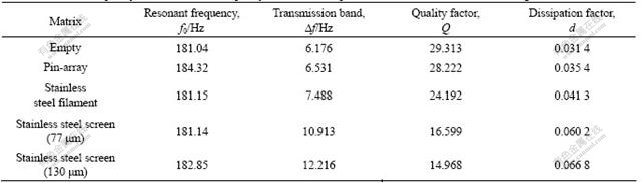
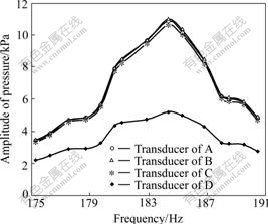
Fig.5 Curves of frequency and amplitude of pressure of regenerator with pin-array at f=184.32 Hz

From the experimental results, the dissipation factor of the pin-array regenerator is the smallest in all  matrixes. Among them, the glass wool that was perpendicular to the wave propagation decays the oscillating pressure mostly and dissipates quickly. There is a maximum dissipation factor and a minimum quality factor for it. Since the real part of complex compliance for pin-array matrix has a maximum value compared with others while its imaginary part is the least, the quality factor of pin-array matrix is the highest with a value of 28.222. It only decreases by 3.7% compared with that of the empty tube (29.313). Furthermore, it is noted that the dissipation factor d_R contributes least to the whole dissipation compared with the dissipation factor d_C, which shows the influence of complex compliance C to the quality of matrix. Thus, the characteristic of compliance is more important than its resistance. Otherwise, the complex compliance has close relationship with the quality factor. It is evident from the experimental investigation on different matrixes of regenerator that the complex compliance is valuable and effective to forecast the ability of energy storage of regenerator.

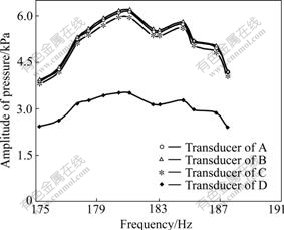
Fig.6 Curves of frequency and amplitude of pressure of regenerator with stainless steel (77 μm) at f=181.14 Hz

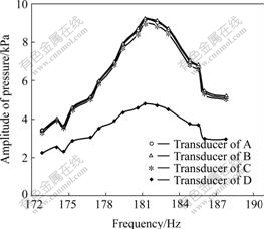
Fig.7 Curves of frequency and amplitude of pressure of regenerator with stainless steel filament at f=181.15 Hz

5 Conclusions

(1) A simple experimental setup is developed to identify the complex compliance and quality factor of regenerator with different matrixes placed in different acoustic systems and the contribution of complex compliance to quality factor is analyzed theoretically and experimentally.

(2) It is demonstrated that different matrixes decay the sound wave differently and the energy dissipation brought by the characteristic of complex compliance of matrix has great effect on the quality of a thermoacoustic engine than resistance.

(3) Among all matrixes used in this experiment, the performance of regenerator with pin-array is the best with the highest quality factor of 28.222. And the glass wool decays the sound wave mostly with the lowest quality factor of 6.7.

(4) Further investigation on other matrixes about influences on energy conversion efficiencies of TAR system would be done in further work in order to search for the appropriate match between regenerator and the whole engine.

[1] SUGITA H, MATSUBARA Y, KUSHINO A, OHNISHI T, KOBAYASHI H, DAI W. Experimental study on thermally actuated pressure wave generator for space cryocooler [J]. Cryogenics, 2004, 44: 431-437.

[2] BACKHAUS S, SWIFT G W. A thermoacoustic-stirling heat engine: Detailed study [J]. J Acoust Soc Am, 2000, 107(6): 3148-3166.

[3] LAFARGE D, LEMARINIER P. Dynamic compressibility of air in porous structures at audible frequencies [J]. J Acoust Soc Am, 1997, 102(4): 1995-2006.

[4] RALPH T M, WALTER C B, BRANDON D T. Measurements and empirical model of the acoustic properties of reticulated vitreous carbon [J]. J Acoust Soc Am, 2005, 117(2): 536-544.

[5] TARNOW V. Dynamic measurements of the elastic constants of glass wool [J]. J Acoust Soc Am, 2005, 118(6): 3672-3678.

[6] TIJANI M E H, SPOELSTRA S, BACH P W. Thermal-relaxation dissipation in thermoacoustic system [J]. Applied Acoustics, 2004, 65: 1-13.

[7] GUO Fang-zhong, LI Qing. Heat dynamics [M]. Wuhan: Huazhong University of Science and Technology Press, 2007: 242-245. (in Chinese)

[8] SWIFT G W. Thermoacoustics: A unifying perspective for some engines and refrigerators [M]. 5th ed. New Mexico: Los Alamos National Laboratory, 2001: 69-70.

[9] WILLEN L A. Measurements of scaling properties for acoustic propagation in a single pore [J]. J Acoust Soc Am, 1997, 101(3): 1388-1397.

[10] WILLEN L A. Measurements of thermoacoustic functions for single pores [J]. J Acoust Soc Am, 1998, 103(3): 1406-1412.

[11] TARNOW V. Measurement of sound propagation in glass wool [J]. J Acoust Soc Am, 1995, 97(4): 2272-2281.

[12] LLINSKII Y A, LIPKENS B, ZABOLOTSKAYA E A. Energy losses in an acoustical resonator [J]. J Acoust Soc Am, 2001, 109(5): 1859-1870.

[13] LIU Yi-cai, ZHOU Jie-min, ZHOU Nai-jun, LIAO Sheng-ming. Investigation on porous frequency of regenerator of microminiature thermoacsoutic refrigerator [J]. Journal of Central South University of Technology, 2005, 12(Suppl.1): 253-255.

[14] ZHANG Chun-ping, WU Feng, DING Guo-zhong, GUO Fang-zhong. Measurements of quality factor in thermoacoustic resonator system [J]. Cryogenics and Superconductivity, 2007, 35(5): 380-382. (in Chinese)

[15] SWIFT G W. Thermoacoustic engines [J]. J Acoust Soc Am, 1988, 84(4): 1145-1180.

[16] FLOYD T L. Electric circuits fundamentals [M]. New Jersey: Prentice Hall, 2001: 552-554.

Foundation item: Projects(50676068, 50576024) supported by the National Natural Science Foundation of China

Received date: 2008-07-24; Accepted date: 2008-09-10

Corresponding author: ZHANG Chun-ping, Doctoral candidate; Tel: +86-27-87542818-611; E-mail: spring_hust@yahoo.com.cn

(Edited by YANG You-ping)

Abstract: In thermoacoustic system, the characteristic of complex compliance of a regenerator has a great influence on energy stored and dissipation of the whole engine. In order to investigate the performance of regenerators with different matrix geometries and materials coupled with different acoustic systems, an experimental measurement and analysis method was presented. By measuring the resonant frequency, the complex compliance and quality factor of five kinds of matrix were experimentally analyzed respectively in the system of loudspeaker-driven thermoacoustic resonator (TAR) with different lengths. The experimental results show that the real part of complex compliance of the regenerator with pin-array has a maximum value among the measured matrixes and its quality factor is the largest (28.222) with the least dissipation factor of 0.035 4. So the pin-array matrix is testified to behave more excellently on the energy conversion than other matrixes. Compared with other factors the complex compliance of a regenerator contributes more to the performance of a thermoacoustic system.