
J. Cent. South Univ. (2020) 27: 180-197
DOI: https://doi.org/10.1007/s11771-020-4287-0

Traffic assignment problem under tradable credit scheme in a bi-modal stochastic transportation network: A cumulative prospect theory approach
HAN Fei(韩飞)1, 2, ZHAO Xiang-mo(赵祥模)2, CHENG Lin(程琳)3
1. School of Automobile, Chang’an University, Xi’an 710064, China;
2. School of Information Engineering, Chang’an University, Xi’an 710064, China;
3. School of Transportation, Southeast University, Nanjing 210096, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract:
The traffic equilibrium assignment problem under tradable credit scheme (TCS) in a bi-modal stochastic transportation network is investigated in this paper. To describe traveler’s risk-taking behaviors under uncertainty, the cumulative prospect theory (CPT) is adopted. Travelers are assumed to choose the paths with the minimum perceived generalized path costs, consisting of time prospect value (PV) and monetary cost. At equilibrium with a given TCS, the endogenous reference points and credit price remain constant, and are consistent with the equilibrium flow pattern and the corresponding travel time distributions of road sub-network. To describe such an equilibrium state, the CPT-based stochastic user equilibrium (SUE) conditions can be formulated under TCS. An equivalent variational inequality (VI) model embedding a parameterized fixed point (FP) model is then established, with its properties analyzed theoretically. A heuristic solution algorithm is developed to solve the model, which contains two-layer iterations. The outer iteration is a bisection-based contraction method to find the equilibrium credit price, and the inner iteration is essentially the method of successive averages (MSA) to determine the corresponding CPT-based SUE network flow pattern. Numerical experiments are provided to validate the model and algorithm.
Key words:
Cite this article as:
HAN Fei, ZHAO Xiang-mo, CHENG Lin. Traffic assignment problem under tradable credit scheme in a bi-modal stochastic transportation network: A cumulative prospect theory approach [J]. Journal of Central South University, 2020, 27(1): 180-197.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-020-4287-01 Introduction
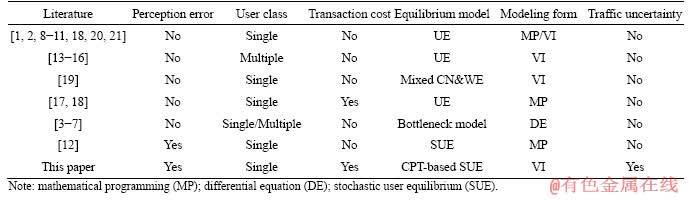
Tradable credit scheme (TCS) is a novel quantity-based instrument for managing traffic demand, which performs better than road congestion pricing (CP) in terms of social equity and revenue neutrality [1, 2]. With playing essentially the same role as CP in managing traffic, TCS has attracted more and more attentions from transportation research community in recent years. To the best of our knowledge, AKAMATSU [3] mathematically analyzed the effect of TCS with traffic equilibrium theory for the first time. He proposed a tradable bottleneck permits scheme (TBPS) to eliminate the queuing delay, and analytically investigate the relationships between TBPS and congestion pricing. However, such a TBPS has some implementation issues. The complicated permit trading market and the controversial market selling scheme can significantly devastate the effect of TBPS. To address these issues, YANG and WANG [1] proposed a new tradable credit distribution and charging scheme with only one type of credit. They quantitatively analyzed how to manage network mobility with TCS in user equilibrium (UE) model framework. This work has been widely extended thereafter for different applications including managing bottleneck congestions [4-7], network design problem under TCS [8-10], achieving special traffic objectives by optimizing TCS [11, 12], considering multiclass users [13-16], market rules and transaction cost (TC) [17, 18], travelers’ loss aversion behaviors [18], mixed Cournot–Nash (CN) and Wardrop-equilibrium (WE) model [19] and some practical implementation strategies [20, 21]. For the most recent reviews on TCS, readers can refer to Ref. [22]. Among these studies, the transportation network equilibrium model is the most commonly used model form, which can describe the traffic flow equilibrium and TCS market equilibrium simultaneously. The modeling methods and basic assumptions are summarized in Table 1.
However, nearly all the existing research mentioned above have neglected the variability of the traffic condition in both demand and supply, and thus travelers were assumed to choose the (perceived) shortest path. In such deterministic scenarios, the traditional UE/SUE model frameworks are capable of addressing the related problems. However, traffic condition is intrinsically stochastic due to the demand and supply uncertainty in a transportation network. The traditional model frameworks fail to capture the uncertainty, thus it is necessary to establish some more advanced models. Such models must be able to describe more realistically how travelers behave in an uncertain traffic environment. Actually, there are various different path choice models based on different behavioral assumptions on travelers’ risk-taking behaviors, such as the expected utility based model [23], the travel time budget (TTB) model [24-26], the late arrival penalty model [27], the mean-excess travel time (METT) model [28] and the cumulative prospect theory (CPT) based models [29-32]. For example, TTB model assumes that travelers always choose the route with the minimum TTB. And TTB is defined by a travel time reliability chance constraint, such that the probability that travel time exceeds the budget is less than a predefined confidence level. METT model assumes that travelers always minimize their METT, which is defined as the conditional expectation of travel times beyond the TTB. For the detailed comparisons and connections among these models, readers can refer to Refs. [28, 31].
As stated in Ref. [31], the CPT-based user equilibrium model can incorporate nearly all the above mentioned models as special cases, thus has very excellent compatibility. With retaining the framework of the expected utility theory, CPT incorporates three behavior characters which are drawn from numerous behavioral experiments: 1) People would distinguish gains from losses before choosing any alternative. Based on certain reference point, the corresponding payoff of choosing each alternative is framed as gain or loss. 2) People always care more about potential losses than potential gains. They are risk averse over gains and risk seeking over losses simultaneously. 3) People tend to underweight average events, but they often overweight extreme, but unlikely events [33-35].
Given that CPT possesses excellent compatibility and provides a well-supported descriptive paradigm for individuals’ decision making under uncertainty, this paper adopts the theory to describe travelers’ route choices in stochastic networks. Furthermore, the endogenous reference points are considered in CPT. With respect to a reference point, the realized payoff of a path is framed into either a gain or loss, and its travel prospect value (PV) can be subsequently determined. Travelers will choose paths with maximal PV, thus they will select the routes in accordance with the particular reference points. The outcome of his or her choice may induce a change in the reference point, which may lead to further adjustment in his or her route choice, and so on. Therefore, a model with endogenous reference points is more competent to predict the long-term stationary equilibrium flow pattern.
Table 1 Modeling technologies of existing literatures
Considering the dramatic growth of private cars, the road traffic congestion becomes more and more serious. It is thus necessary and urgent to enhance the use of public transit for the sake of congestion mitigation and sustainable development of transportation system. Based on this consideration, the multi-modal transportation network is considered in this paper. Besides, the transaction costs (TC) of selling/buying credits are also considered to further improve the practicability of the study.
The contributions of this paper are threefold. First, a novel CPT-based traffic assignment model is established for a stochastic bi-modal transportation network under a given TCS. The endogenous reference points are considered in CPT, and meanwhile, the TC is considered in the credit trading market. Second, a tailored solution algorithm is developed to solve the proposed model. The algorithm contains two-level iterations, of which the outer iteration is a bisection-based contraction method to find the equilibrium credit price, and the inner iteration is essentially the MSA to determine the CPT-based SUE network flow pattern. Third, in order to avoid overestimating the travel demand on road sub-network in some extreme cases, the weighted average of the generalized path costs is used in the mode-split model, rather than the satisfaction function.
The remainder of this paper is organized as follows. Section 2 describes the CPT-based multi-modal equilibrium assignment problem under given TCS; Section 3 proposes a heuristic solution algorithm; Section 4 presents some numerical examples. In the final section, some concluding comments are provided.
2 CPT-based SUE model for bi-modal traffic network under TCS
2.1 Network representation and assumptions
Consider a general strongly connected road network G=(N, A), with a set N of nodes, and a set A of directed links. Let the set of O-D pairs be denoted by W, and the traffic demand on road network for O-D pair w∈W be denoted by 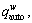 let Rw denote the set of all paths between O-D pair w∈W, let
let Rw denote the set of all paths between O-D pair w∈W, let 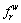 denote the flow on path r∈Rw, and let va denote the traffic flow on link a∈A. The following flow conservation equations should be satisfied:
denote the flow on path r∈Rw, and let va denote the traffic flow on link a∈A. The following flow conservation equations should be satisfied:
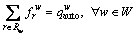 (1)
(1)
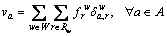 (2)
(2)
 (3)
(3)
where  which is an element of the link/path incidence matrix, is equal to 1 if path r∈Rw uses link a∈A and 0 otherwise.
which is an element of the link/path incidence matrix, is equal to 1 if path r∈Rw uses link a∈A and 0 otherwise.
Assume that the road network G=(N, A) is accompanied by a rail network G′=(N′, A′), where N′ and A′ denote the set of nodes and directed links on the rail network. The O-D pairs on rail network are the same as those on road network, i.e., W. For simplicity, it is assumed that only one exclusive metro line exists between each O-D pair. The travel time on metro line between O-D pair w∈W is denoted by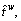 w∈W which is a flow-independent constant. Moreover, there exists a fare denoted by
w∈W which is a flow-independent constant. Moreover, there exists a fare denoted by 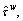 w∈W on each metro line, which is also flow-independent and predetermined. Let
w∈W on each metro line, which is also flow-independent and predetermined. Let 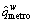 be the traffic demand on rail network for O-D pair w∈W, thus it also denotes the path flow on the metro line between O-D pair w∈W. Thus, the O-D demands on two sub-networks fulfill this condition:
be the traffic demand on rail network for O-D pair w∈W, thus it also denotes the path flow on the metro line between O-D pair w∈W. Thus, the O-D demands on two sub-networks fulfill this condition:
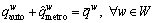 (4)
(4)
where 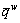 is a constant representing the upper bound of traffic demand between OD pair w∈W. In this bi-modal transportation network, travelers would make their mode-choice based on overall travel impedance of using each mode.
is a constant representing the upper bound of traffic demand between OD pair w∈W. In this bi-modal transportation network, travelers would make their mode-choice based on overall travel impedance of using each mode.
Assume that the government implements TCS to manage network mobility, and levies credit charges only on road network to promote transit trip-mode and improve the roadway congestion. Let K denote the total amount of credits issued to travelers initially, and each traveler between O-D pair w∈W is eligible to get some amount of credits,denoted as fw, thus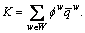 Let ka denote the credit charges on link a∈A, thus k=[ka, a∈A] denotes a link credit charge scheme on road network. Hence, the notation (K, k) represents an entire TCS. Since no credit is charged on rail sub-network, the feasible network flow patterns exist under any given TCS [1].
Let ka denote the credit charges on link a∈A, thus k=[ka, a∈A] denotes a link credit charge scheme on road network. Hence, the notation (K, k) represents an entire TCS. Since no credit is charged on rail sub-network, the feasible network flow patterns exist under any given TCS [1].
In road network, the link performance function is assumed to be the Bureau of Public Roads (BPR) function, i.e., 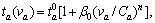 where
where 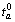 is the free-flow travel time on link a∈A and Ca is the link capacity. Thus, the path travel time
is the free-flow travel time on link a∈A and Ca is the link capacity. Thus, the path travel time 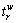 on route r∈Rw can be obtained,
on route r∈Rw can be obtained,
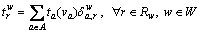 (5)
(5)
In fact, variability of travel time in road network often arises from an array of different sources: the stochastic traffic demand results in the varying network flows, or the link capacity of the road network is degraded unpredictably by accidents and incidents. In such situations, the O-D demands or link capacity are random variables, the corresponding notations defined above can represent their mean values. Note that with different uncertainty sources, the analytic expression of the mean link travel time ta, a∈A should be derived from the specific random variables, e.g., stochastic traffic demand or link capacity, based on BPR function [24, 25].
Specifically, if the total O-D demand is assumed to be the source of uncertainty, and it follows a normal distribution, i.e., 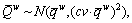 where
where 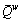 is the stochastic O-D demand and cv denotes the coefficient of variance of the demand. The path flows also follow normal distributions and have the same coefficient of variance with the O-D demand under a very mild condition of constant path-choice probability [25, 31]. Furthermore, the probability distributions of path travel times can be derived as:
is the stochastic O-D demand and cv denotes the coefficient of variance of the demand. The path flows also follow normal distributions and have the same coefficient of variance with the O-D demand under a very mild condition of constant path-choice probability [25, 31]. Furthermore, the probability distributions of path travel times can be derived as:
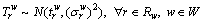 (6)
(6)
where 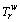 and
and 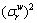 denote the stochastic path travel time and its variance on path r∈Rw, with the mean value
denote the stochastic path travel time and its variance on path r∈Rw, with the mean value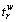 and variance
and variance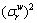 being calculated via the following equations:
being calculated via the following equations:
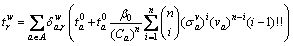 (7)
(7)
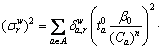
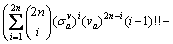
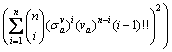 (8)
(8)
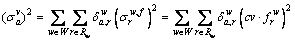 (9)
(9)
where 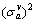 and
and 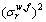 are the variances of the link and path flows respectively. As mentioned above, va and
are the variances of the link and path flows respectively. As mentioned above, va and 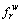 denote the mean values of link and path flows, thus the probability distribution of path travel time is actually parameterized by the mean values of link flow patterns.
denote the mean values of link and path flows, thus the probability distribution of path travel time is actually parameterized by the mean values of link flow patterns.
2.2 Generalized path cost in bi-modal network
In this study, the generalized path travel cost of road network comprise two parts, i.e., time PV and credit cost, while the generalized path travel cost of rail network comprise three parts, i.e., time PV, fare expense and credit income, as shown in Figure 1. Each part of travel cost is introduced in the following subsection. Note that the generalized path costs determine not only the travel demands of all trip modes, but also the network flow patterns in the bi-modal transportation network. Conversely, the network flow patterns would also influence the credit price in the credit trading market, as well as the path travel time and the corresponding path PV in the bi-modal network.
2.2.1 Path-travel-time-based reference points and prospect values
Assume that travel times are random and their probability distributions are known to travelers, and that travelers have the same risk-taking attitude or on-time arrival probability [29-32]. Travelers have to make a budgeted time for a specific trip due to travel time variability. The budgeted time reflects their probabilistic belief on travel times based on their preferences, and can thus potentially serve as reference points. More specially, when they depart from their origin, travelers use the budgeted time as a reference point to determine the gain or loss of each path based on its travel time distribution, and make their route choices accordingly.
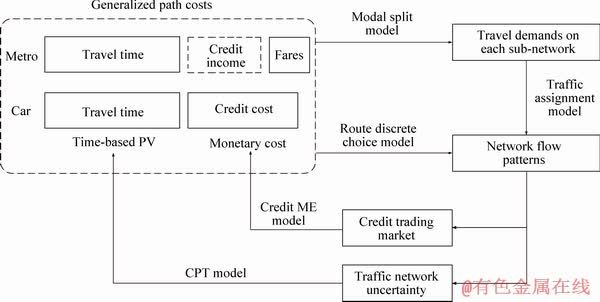
Figure 1 Generalized path costs and related models
Mathematically, suppose that travelers’ desired on-time arrival probability is no less than ζ, and the corresponding minimal budgeted time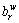 for taking path r∈Rw can be written as:
for taking path r∈Rw can be written as:
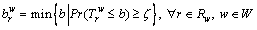 (10)
(10)
Clearly, the minimal budgeted time 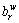 is exactly the ζ th percentile value of the travel time of path r∈Rw. Since there exist multiple paths between each O-D pair, the path-travel-time-based reference point
is exactly the ζ th percentile value of the travel time of path r∈Rw. Since there exist multiple paths between each O-D pair, the path-travel-time-based reference point  between O-D pair w∈W is assumed to be a function of the budgeted time
between O-D pair w∈W is assumed to be a function of the budgeted time 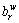 for all paths between this O-D pair. In this study, the minimum of the budgeted times of all paths is adopted as the reference point between O-D pair w∈W,
for all paths between this O-D pair. In this study, the minimum of the budgeted times of all paths is adopted as the reference point between O-D pair w∈W,
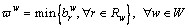 (11)
(11)
Essentially, the reference points are based upon the network flow pattern. The reference points will remain constant and are consistent in network equilibrium state, with the resulting CPT-based equilibrium flow pattern and the corresponding path travel time distributions.
Consider a trip between O-D pair w∈W with  as the reference point. The relative payoff for choosing path r∈Rw can be defined as
as the reference point. The relative payoff for choosing path r∈Rw can be defined as 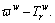 As postulated in CPT, travelers may consider the outcome of a trip as a gain, if the travel time is less than the reference point; as a loss if otherwise. To capture this kind of distortion in the perception of the outcomes, the S-shaped value function gw(·) can be defined as:
As postulated in CPT, travelers may consider the outcome of a trip as a gain, if the travel time is less than the reference point; as a loss if otherwise. To capture this kind of distortion in the perception of the outcomes, the S-shaped value function gw(·) can be defined as:
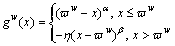 (12)
(12)
where α and β determine the degree of diminishing sensitivity of the value function. Typically, 0<α, β<1 and thus the value function exhibits risk aversion over gains and risk seeking over losses. The parameter η≥1 measures the degree of loss-aversion, indicating that individuals are more sensitive to losses than gains. The variable x denotes a realized value of random variable 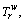 r∈Rw, w∈W.
r∈Rw, w∈W.
In the CPT context, travelers make their decisions based on the outcome probabilities they perceive, and typically, small probabilities are over-weighted while moderate and high probabilities are under-weighted [33-35]. In this paper, Prelec’s probability weight function is used [34]:
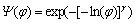 (13)
(13)
where Ψ(φ) and φ denote the perceived probability and actual probability of an event respectively. The parameter γ∈(0, 1) represents the distortion level in probability judgment in the decision making process.
With the above value and probability weight functions, the travel-time-based PV for choosing path r∈Rw can be written as:
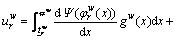
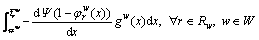 (14)
(14)
where  is the time-based PV for choosing path r∈Rw;
is the time-based PV for choosing path r∈Rw; 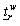 and
and 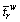 are respectively the lower and upper bounds of the travel time on path r∈Rw. In this study,
are respectively the lower and upper bounds of the travel time on path r∈Rw. In this study, 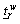 is assumed to be the free-flow travel time and
is assumed to be the free-flow travel time and 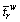 is the 99.9999% of the random travel time
is the 99.9999% of the random travel time 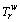 . Note that the time PV
. Note that the time PV  of path r∈Rw is deterministic, even if travel time is stochastic. Clearly,
of path r∈Rw is deterministic, even if travel time is stochastic. Clearly,  is also a function of network flow patterns.
is also a function of network flow patterns.  is the cumulative distribution function of
is the cumulative distribution function of 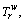 i.e.,
i.e.,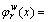
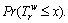
In rail network, since the travel time on metro line is a constant rather than random variable, the time PV cannot be directly calculated based on Eq. (14). However, if we view the constant as a special random variable with probability density function 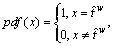 the time PV on each metro line can be determined in a similar way as presented above. Under this circumstance, the probability weight function becomes Ψ(φ)=
the time PV on each metro line can be determined in a similar way as presented above. Under this circumstance, the probability weight function becomes Ψ(φ)=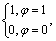 and the PV function would eventually
and the PV function would eventually
reduce to the value function. Specifically, the expression of time-based PV on the metro line between O-D pair w∈W can be written as:

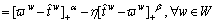 (15)
(15)
where [a]+=a if a≥0, and 0 otherwise. In fact, Eq. (15) can be derived from the definition of PV of an alternative with finite discrete outcomes [35]. Furthermore, CONNORS and SUMALEE [30] provide an explicit derivation and show that Eq. (14) reproduces Eq. (15) when the probability density function represents a discrete distribution of outcomes [30].
2.2.2 Path credit costs in bi-modal network
In the bi-modal network, the government charges credits only on road network in order to promote rail trip-mode and improve the roadway congestion. Therefore, travelers have to bear some credit costs if choose auto-mode, or they can get some income by selling the credit if choose rail-mode. Moreover, travelers have to pay some transaction costs when trading credits.
Using mathematical expressions, for the travelers choosing rail-mode between O-D pair w∈W, the income they can get can be written as  where
where 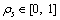 is the TC rate of selling credits. The notation p is credit price measured in money unit.
is the TC rate of selling credits. The notation p is credit price measured in money unit.
Besides, the credit cost on the path of road network can be expressed as:
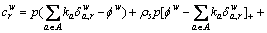
 (16)
(16)
where 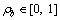 is the TC rate of buying credits. Equation (16) indicates that the travelers need to buy extra credits when choosing the route charging more credit than they possess, while they can sell the leftover credits when choosing the route charging less.
is the TC rate of buying credits. Equation (16) indicates that the travelers need to buy extra credits when choosing the route charging more credit than they possess, while they can sell the leftover credits when choosing the route charging less.
2.2.3 generalized path costs of bi-modal network
Since the generalized path travel cost involves time PV and monetary cost, a conversion coefficient must be introduced to make them additive. In this paper, the conversion coefficient is assumed to be identical for all travelers. Note that PV and credit income represent utility rather than disutility, thus a negative sign must be added to them when calculating the generalized path travel cost. Moreover, assume that travelers have perception errors on the generalized path travel cost, and the perception errors follow a certain probability distribution, e.g., Gumbel or Normal distribution.
For road sub-network, the perceived generalized travel cost 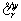 on path r∈Rw can be formulated as the following expression:
on path r∈Rw can be formulated as the following expression:
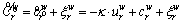

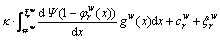 (17)
(17)
where 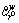 is the expected generalized travel cost on path r∈Rw, i.e.,
is the expected generalized travel cost on path r∈Rw, i.e., 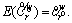 The notation κ is the conversion coefficient between time-based PV and monetary cost. Without loss of generality, set κ=1. The notation
The notation κ is the conversion coefficient between time-based PV and monetary cost. Without loss of generality, set κ=1. The notation 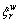 is traveler’s perception error of road sub-network, with zero mean
is traveler’s perception error of road sub-network, with zero mean 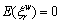 and constant variance
and constant variance 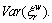
For rail network, the perceived generalized travel cost on metro line between O-D pair w∈W can be expressed as:
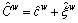
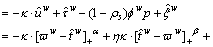
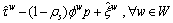 (18)
(18)
where 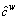 is the expected generalized travel cost on metro line between O-D pair w∈W, i.e.,
is the expected generalized travel cost on metro line between O-D pair w∈W, i.e., 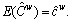 The notation
The notation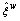 is traveler’s perception error of rail sub-network. Actually, the travelers can easily get perfect information on the travel cost on rail sub-network, thus their perception errors in this case can be taken as zero.
is traveler’s perception error of rail sub-network. Actually, the travelers can easily get perfect information on the travel cost on rail sub-network, thus their perception errors in this case can be taken as zero.
2.3 Mode-split model
In the bi-modal network, travelers are assumed to choose a travel mode before they make the trip on a specific route. In this study, a binary logit model is selected for the mode-split, in view of its simplicity for use and popularity in the mode-split studies [36-38]. Thus, for any O-D pair w∈W, the travel demands on road sub-network are equal to:
 (19)
(19)
where 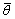 is the dispersion parameter of mode choice;
is the dispersion parameter of mode choice; 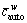 is the weighted average of the expected generalized path costs between O-D pair w∈W in road sub-network, i.e.,
is the weighted average of the expected generalized path costs between O-D pair w∈W in road sub-network, i.e., 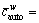
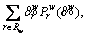 where
where 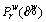 is choice probability of the path r∈Rw evaluated at
is choice probability of the path r∈Rw evaluated at 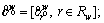 and λw>0 is the exogenous attractiveness of metro line between O-D pair w∈W. Clearly, a large
and λw>0 is the exogenous attractiveness of metro line between O-D pair w∈W. Clearly, a large 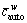 (i.e., auto-mode travel cost), a small
(i.e., auto-mode travel cost), a small 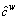 (i.e., metro- mode travel cost) or a large λw (i.e., metro attractiveness) yields a large choice proportion of metro traffic.
(i.e., metro- mode travel cost) or a large λw (i.e., metro attractiveness) yields a large choice proportion of metro traffic.
Note that in road sub-network, the weighted average 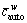 of the generalized path costs is taken as the auto-mode travel cost for O-D pair w∈W, rather than the commonly used satisfaction function
of the generalized path costs is taken as the auto-mode travel cost for O-D pair w∈W, rather than the commonly used satisfaction function 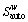 [2, 37]. According to Ref. [39], the inequality
[2, 37]. According to Ref. [39], the inequality 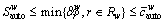 always holds, thus the inequality
always holds, thus the inequality 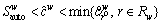 may exist in some extreme cases. Therefore, the travel demands of road sub-network might be overestimated unreasonably in such cases, if
may exist in some extreme cases. Therefore, the travel demands of road sub-network might be overestimated unreasonably in such cases, if 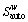 is adopted in Eq. (19).
is adopted in Eq. (19).
2.4 Variational inequality model for CPT-based bi-modal SUE with TCS
For the bi-modal network under a given TCS, a stationary equilibrium state can be achieved when no traveler can improve his or her perceived generalized path cost by unilaterally changing routes. Mathematically, the CPT-based network equilibrium (CPT-NE) conditions can be expressed as:
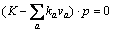 (20)
(20)
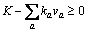 (21)
(21)
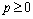 (22)
(22)
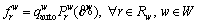 (23)
(23)
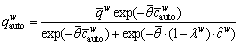 (24)
(24)
As well as Eqs. (1)-(4) and (17)-(18).
Equations (20)-(22) represent the credit market equilibrium (ME) conditions, and Eqs. (1)-(4), Eqs. (17)-(18), Eqs. (23)-(24) represent the CPT-based bi-modal SUE conditions. At CPT-NE, the travelers no longer adjust their reference points, which thus remain constant and are consistent with the CPT-NE flow pattern and the corresponding travel time distributions. Note that 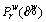 has analytic forms, i.e.,
has analytic forms, i.e.,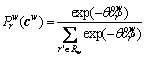 under the assumption of Gumbel distributed perception errors, while
under the assumption of Gumbel distributed perception errors, while 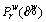 cannot be expressed analytically under the assumption of Normal distributed perception errors, but can be calculated with Monte Carlo method [39].
cannot be expressed analytically under the assumption of Normal distributed perception errors, but can be calculated with Monte Carlo method [39].
The CPT-NE conditions defined above can be formulated as the following variational inequality (VI) model:
Find 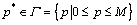 such that:
such that:
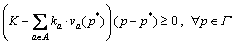 (25)
(25)
where M is a predetermined large number, which is far greater than the potential maximum credit price. Note that M does not influence the final solution to the VI model, as M is just a nonbinding upper bound; meanwhile, it is easy to know if M is big enough, via the solution algorithm presented in the next section. Notation 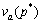 is the SUE link flow pattern of road sub-network under the given parameter p*. In fact, a parameterized fixed-point (FP) model represented by Eqs. (1)-(4), (17)-(18) and Eqs. (23)-(24) is embedded in the VI model (25), which is exactly a CPT-based bi-modal SUE sub-problem. Thus, va(p*) is also the solution to the parameterized FP model, with the given credit price p*.
is the SUE link flow pattern of road sub-network under the given parameter p*. In fact, a parameterized fixed-point (FP) model represented by Eqs. (1)-(4), (17)-(18) and Eqs. (23)-(24) is embedded in the VI model (25), which is exactly a CPT-based bi-modal SUE sub-problem. Thus, va(p*) is also the solution to the parameterized FP model, with the given credit price p*.
The equivalence between the VI model (25) and the CPT-NE conditions Eqs. (1)-(4), (17)-(18) and (20)-(24) can be established in a similar way to that (given by Proposition 4) in Ref. [40], thus omitted here. Assume that the PV function is continuous with respect to 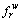 (or va), which is a commonly used assumption in literatures [30-32]. Thus, the generalized path travel cost is also continuous with respect to
(or va), which is a commonly used assumption in literatures [30-32]. Thus, the generalized path travel cost is also continuous with respect to 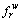 (or va), then the existence of SUE network flow pattern can be guaranteed. Based on Proposition 2 in Ref. [40],it can be further inferred that the function
(or va), then the existence of SUE network flow pattern can be guaranteed. Based on Proposition 2 in Ref. [40],it can be further inferred that the function 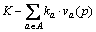 is continuous with respect to p.
is continuous with respect to p.
With the non-empty, convex and compact set Γ, it can be concluded that the VI model (25) has at least one solution [41].
The uniqueness of the ME credit price can be guaranteed if there exists at least one OD pair w∈W whose realized positive demand 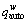 of road sub-network does not reach its upper-bound
of road sub-network does not reach its upper-bound 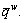 The proof is similar to the Proposition 4 in Ref. [1]. The uniqueness of the SUE network flow pattern is not established in this paper, as the PV function may be not strictly monotone with respect to
The proof is similar to the Proposition 4 in Ref. [1]. The uniqueness of the SUE network flow pattern is not established in this paper, as the PV function may be not strictly monotone with respect to 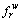 (or va) due to the complicated function form.
(or va) due to the complicated function form.
3 Solution algorithm
Considering that the VI model contains double-layer structures, and that the ME credit price is determined by the relationship of supply and demand in the credit market, a heuristic solution algorithm is developed based on these properties. The algorithm contains two-level iterations: The outer iteration is a bisection-based contraction method to find the ME credit price, and the inner iteration is essentially the MSA to determine the corresponding CPT-based SUE network flow pattern.
[Outer Iteration]:
Step 0: Initialization. Let 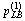 and
and 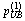 be the initial lower bound and upper bound of credit price, respectively. Set
be the initial lower bound and upper bound of credit price, respectively. Set 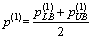 be initial credit price, and then set n=1;
be initial credit price, and then set n=1;
Step 1: Invoking inner iteration. With the current credit price p(n), the original problem reduces to a bi-modal CPT-based SUE sub-problem, which can be solved by implementing the inner iteration;
Step 2: Checking the stopping criterion. If at least one of the following two stopping criteria holds,
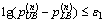 or (26)
or (26)
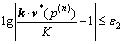 (27)
(27)
where ε1 and ε2 are the prescribed convergence tolerances. Then, terminate the iteration and output the current credit price p(n), as well as the corresponding SUE link flow pattern v*(p(n)); otherwise, go to Step 3;
Step 3: Updating the credit price bounds and credit price. Update the lower bound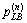 and upper bound
and upper bound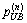 of credit price according to the following rules:
of credit price according to the following rules:
if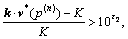 then
then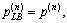 and
and 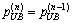 ;
;
else if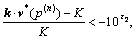 then
then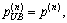 and
and 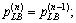
Then update the credit price 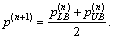 Let n=n+1, and go back to Step 1.
Let n=n+1, and go back to Step 1.
[Inner Iteration]:
Step 1.0 Initialization
Set m=1 and specify an initial path flow pattern f(1) and convergence tolerance ε3;
Step 1.1 Determining reference points between each OD pair. Based on the current road flow pattern f(m), calculate the probability distributions of road path travel time according to (7-9). Further, determine the reference points that satisfy the constraints (10-11);
that satisfy the constraints (10-11);
Step 1.2 Calculating generalized path cost on each path. Calculate the time PV and credit cost (or income) for each path of the bi-modal network according to Eqs. (14)-(16), with the current p(n). Then, the generalized path cost 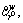
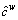 can be obtained by Eqs. (17) and (18);
can be obtained by Eqs. (17) and (18);
Step 1.3 Mode split. Determine the current travel demands 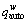 and
and 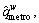 respectively, for auto-mode and metro-mode by the Eq. (19) ;
respectively, for auto-mode and metro-mode by the Eq. (19) ;
Step 1.4 Determining search direction. Based on the current travel demands and generalized path cost, obtain the search direction f(m) by implementing stochastic network loading via the Eq. (23);
Step 1.5 Convergence check:
If 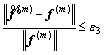 , then stop and output the current path flow pattern f (m) (i.e., f (m)(p(n))). Otherwise, go to step 1.6;
, then stop and output the current path flow pattern f (m) (i.e., f (m)(p(n))). Otherwise, go to step 1.6;
Step 1.6 Updating path flows. Update the path flow pattern by 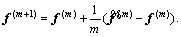 Set m=m+1, and then go to step 1.1.
Set m=m+1, and then go to step 1.1.
Remarks: The stop criterion in Eq. (26) can be used to verify the appropriateness of the preset initial bounds of credit price, i.e.,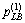 and
and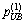 . Meanwhile, Eq. (26) can also prevent the algorithm sinking into dead circulation, if the initial interval
. Meanwhile, Eq. (26) can also prevent the algorithm sinking into dead circulation, if the initial interval 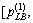
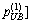 doesn’t contain the final ME credit price p*. Generally speaking, it is only the stop criterion in Eq. (27) that would be satisfied when the algorithm converges, if the initial interval is appropriate. And it is only when the undesired situation
doesn’t contain the final ME credit price p*. Generally speaking, it is only the stop criterion in Eq. (27) that would be satisfied when the algorithm converges, if the initial interval is appropriate. And it is only when the undesired situation 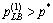 or
or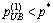 occurs, that the stop criterion in Eq. (26) could be satisfied. Under this circumstance, Eq. (27) could never be satisfied, thus Eq. (26) can stop the dead circulation of the algorithm.
occurs, that the stop criterion in Eq. (26) could be satisfied. Under this circumstance, Eq. (27) could never be satisfied, thus Eq. (26) can stop the dead circulation of the algorithm.
Note that the reasonableness of the stop criteria in Step 2 must rely on the updating rules in Step 3 in outer iteration. Meanwhile, the appropriateness of 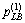 and
and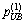 can be verified by using the following rules similar to those in Step 3.
can be verified by using the following rules similar to those in Step 3.
Specifically, 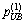 is set too low and must increase if
is set too low and must increase if 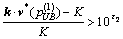 holds, whereas
holds, whereas 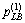 is set too high and must decrease if
is set too high and must decrease if 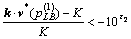 holds.
holds.
According to Proposition 1 in Ref. [40], it can be easily inferred that the function 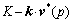 is monotonically increasing with respect to p. Thus, function k·v*(p) is monotonically decreasing with respect to p, given that total credit amount K is constant. Therefore, the outer iteration can definitely find the ME credit price after finite iterations. The inner iteration is essentially the well-known MSA, which demonstrated a good convergence property in our numerical experiments.
is monotonically increasing with respect to p. Thus, function k·v*(p) is monotonically decreasing with respect to p, given that total credit amount K is constant. Therefore, the outer iteration can definitely find the ME credit price after finite iterations. The inner iteration is essentially the well-known MSA, which demonstrated a good convergence property in our numerical experiments.
4 Numerical experiments
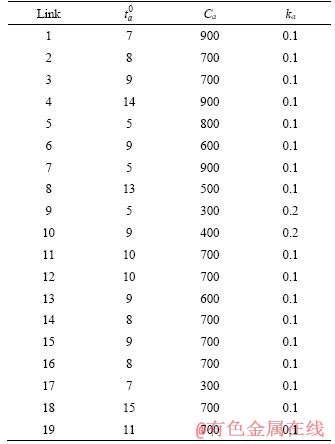
The Nguyen-Dupuis network is used as the test network, as shown in Figure 2. The bi-modal network consists of 13 nodes, 19 road links (solid line) and 4 metro links (dashed line). There are 4 O-D pairs in the bi-modal network, 1–2, 1–3, 4–2 and 4–3. The numbers of paths of road sub-network between those O-D pairs are 8, 6, 5, and 6, respectively. There exists only one exclusive metro line between each O-D pair. The mean O-D demands are q12=800, q13=1600, q42=1200, q43=400. The average link travel time function of road sub-network is the standard BPR function, i.e.,  and the link characteristics are given in Table 2. The constant travel times
and the link characteristics are given in Table 2. The constant travel times 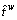 on each metro line are 35, 40, 35, 40, respectively, and the transit fares
on each metro line are 35, 40, 35, 40, respectively, and the transit fares  are 5, 5, 4, 6, respectively. The metro attractiveness λw is 0.04, 0.05, 0.06, 0.04, respectively.
are 5, 5, 4, 6, respectively. The metro attractiveness λw is 0.04, 0.05, 0.06, 0.04, respectively.
The TCS is assumed to be imposed in the bi-modal transportation network, and total credit amount is K=900, initial credit amount fw for the traveler of each O-D pair is 0.25, 0.2, 0.25 and 0.2, respectively. The credit is charged only on links of road sub-network, and the charge ka is presented in Table 2. The TC rates are ρs=0.08, ρb=0.1.
Assume that the path travel times are stochastic on road sub-network, due to the daily road traffic incidents. And the probability distribution is assumed to be following the normal distribution, i.e.,
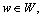 and cv=[0.5, 0.01, 0.15, 0.2, 0.1, 0.3, 0.001, 0.01; 0.3, 0.01, 0.3, 0.5, 0.02, 0.2; 0.1, 0.4, 0.001, 0.35, 0.02; 0.6, 0.1, 0.3, 0.05, 0.01, 0.1].
and cv=[0.5, 0.01, 0.15, 0.2, 0.1, 0.3, 0.001, 0.01; 0.3, 0.01, 0.3, 0.5, 0.02, 0.2; 0.1, 0.4, 0.001, 0.35, 0.02; 0.6, 0.1, 0.3, 0.05, 0.01, 0.1].
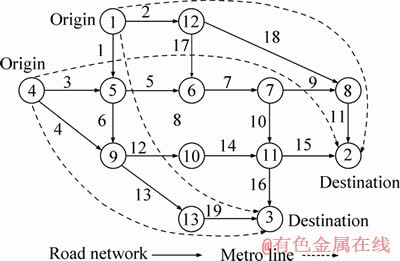
Figure 2 Nguyen-Dupuis network
Table 2 Link characteristics of road sub-network
Assume that travelers’ desired on-time arrival probability is no less than ζ=95%. The parameters of the value function in Eq. (12) are assumed to be α=β=0.52, η=2.25, and the parameter of probability weight function in Eq. (13) is γ=0.74. The logit-based stochastic network loading is adopted with dispersion parameter θ=0.1, and the dispersion parameter for mode-split model is 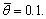
Based on the solution algorithm proposed above, the equilibrium solution is obtained after 7 outer iterations and totally 51 inner iterations in this numerical example, as shown in Figure 3. At CPT-NE, the ME credit price p*=3.9375 and SUE link flow pattern vT=[629.20, 441.01, 482.41, 235.81, 757.04, 354.57, 716.70, 400.35, 236.03, 480.67, 317.04, 333.43, 256.94, 733.78, 506.11, 708.34, 360.01, 81.00, 256.94]. Meanwhile, the travel demands 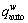 on road sub-network are 341.94, 728.28, 481.21, 237.00, and the reference points
on road sub-network are 341.94, 728.28, 481.21, 237.00, and the reference points  are 38.70, 45.18, 41.41 and 34.65, respectively.
are 38.70, 45.18, 41.41 and 34.65, respectively.

Figure 3 Convergence curve of solution algorithm
In order to reveal the impacts of various parameters on equilibrium solutions, the equilibrium solutions under different parameter values are compared in this study, as shown in Figures 4-8. Specifically, Figure 4 compares the equilibrium solutions under different risk levels (i.e., on-time arrival probability ζ); Figure 5 compares those under different route-choice dispersion parameters θ; Figure 6 compares those under different mode-choice dispersion parameters 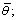 Figure 7 compares those under different TC rates (ρb and ρs); Figure 8 compares those under different link-based credit charge schemes k (with K fixed).
Figure 7 compares those under different TC rates (ρb and ρs); Figure 8 compares those under different link-based credit charge schemes k (with K fixed).
Figure 4 shows that the ME credit price and reference points will increase with the increasing of risk level. Thus, with the risk level increasing, the path credit costs also increase. It is interesting to see that the generalized path travel costs decrease while both the PV and credit costs are increasing, which indicates the decrease of generalized path travel costs caused by the rising PV is greater than the increase caused by the rising credit cost.
It can be seen from Figure 5 that the impacts of path-choice dispersion parameter θ on equilibrium solutions are more complicated. With the increasing of θ, both increasing and decreasing phases arise for ME credit price and reference points, as shown in Figures 5(a) and (c). Besides, the SUE path flow approaches to the UE path flow when θ=1, as shown in Figures 5(d) and (f).
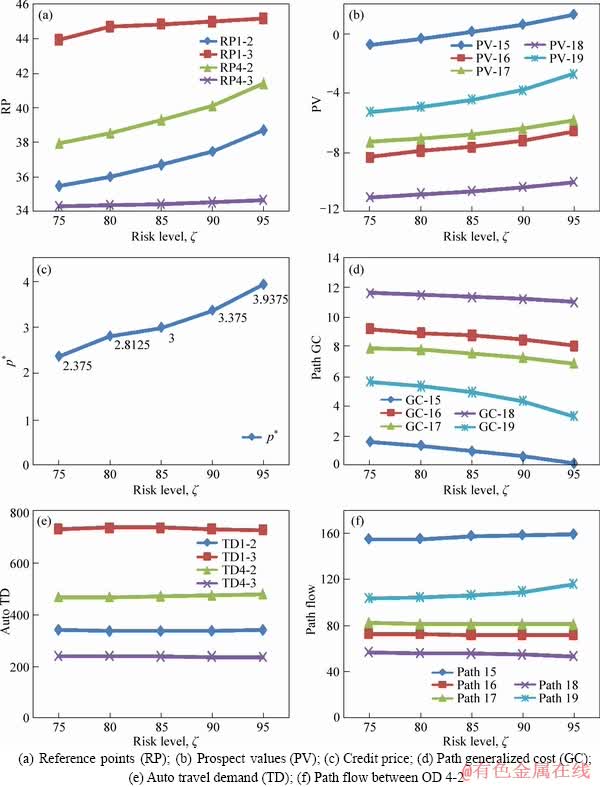
Figure 4 Comparison of solutions under different risk level values ζ:
Figure 6 shows that the mode-split dispersion parameter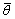 has very little influence on the reference points and PV. However, the auto-mode travel demands of road sub-network, as well as the ME credit price, are influenced by
has very little influence on the reference points and PV. However, the auto-mode travel demands of road sub-network, as well as the ME credit price, are influenced by 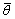 to a large extent. With
to a large extent. With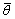 increasing, the travelers become more sensitive to the travel cost differences between the two traffic modes, and more travelers will choose the metro-mode. Thus, more credits will be left, and the credit price will decrease. As shown in Figure 6(c), the ME credit price will decrease to zero when
increasing, the travelers become more sensitive to the travel cost differences between the two traffic modes, and more travelers will choose the metro-mode. Thus, more credits will be left, and the credit price will decrease. As shown in Figure 6(c), the ME credit price will decrease to zero when  =0.7.
=0.7.
Figures 7(a)-(d) shows the equilibrium solutions under different TC rates ρb of buying credit, and Figures 7(e)-(h) shows those under different TC rates ρs of selling credit. It can be seen from Figure 7 that both reference points and PV have little change under different TC rates. However, the ME credit price will decrease with the increasing of ρb, while it will increase with the increasing of ρs. Figures 7(c) and (d) show that the path credit costs still increase even if the credit price decreases, which indicates that the increase of path credit cost caused by the rising TC is greater than the decrease caused by the declining credit price.
Figure 5 Comparison of solutions under different dispersion parameter θ:
Figure 8 shows that the generalized path travel costs increase and the travel demands decrease in road sub-network, with the credit charges k increasing. These results indicate that TCS can effectively regulate the trip mode choice, thus is promising in improving service level of multimodal transportation system. Interestingly, the ME credit price may increase or decrease with k increasing, which demonstrates that the supply-demand relationship of credit market becomes more complicated in multimodal transportation network.

Figure 6 Comparison of solutions under different mode-split dispersion parameters  :
:
5 Conclusions
This paper has applied the cumulative prospect theory to describe travelers’ route choice behaviors in a stochastic bi-modal transportation network under a given TCS. In the bi-modal network, traveler’s generalized path travel cost consists of PV and credit cost in road sub-network, while it consists of PV, transit fare and credit income in rail sub-network. The CPT-based network equilibrium conditions are proposed to describe the stationary state of the bi-modal network based on the generalized path travel cost. At the equilibrium state, the reference points and PV will remain constant, as both of them depend on the equilibrium flow pattern ultimately. An equivalent VI model is then established for the CPT-based network equilibrium conditions, in which a parameterized FP model is embedded as a subproblem. Some theoretical analyses are presented to guarantee the existence and uniqueness of the equilibrium solution. Considering that the VI model contains two-layer structures, and that the ME credit price is determined by the relationship of supply and demand in the credit market, a heuristic solution algorithm is developed based on these properties. The algorithm contains two-level iterations, of which the outer iteration is a bisection-based contraction method to find the ME credit price, and the inner iteration is essentially the MSA to determine the corresponding CPT-based SUE network flow pattern.
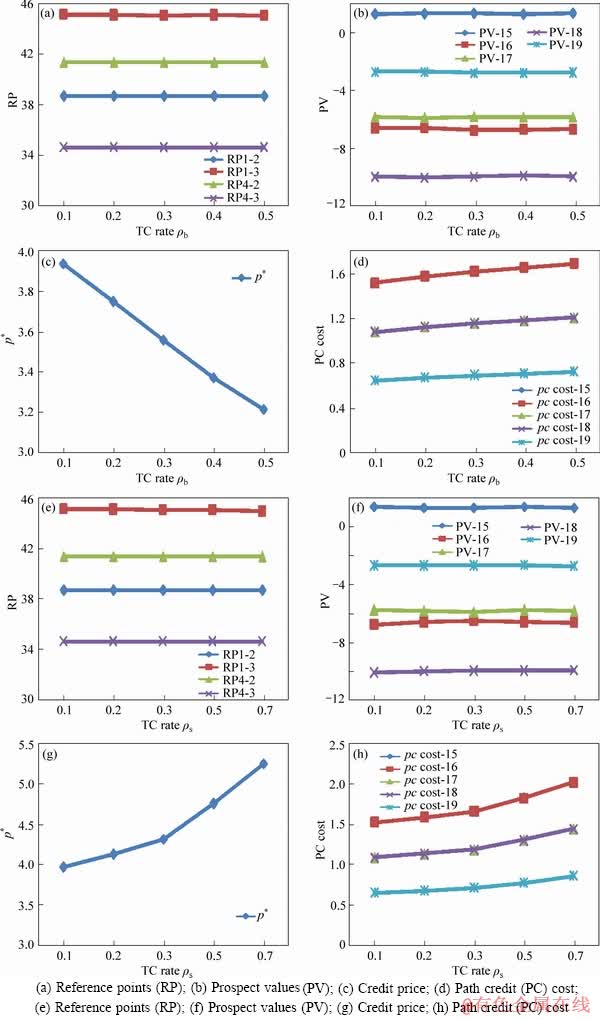
Figure 7 Comparison of solutions under different TC rates (ρb and ρs):
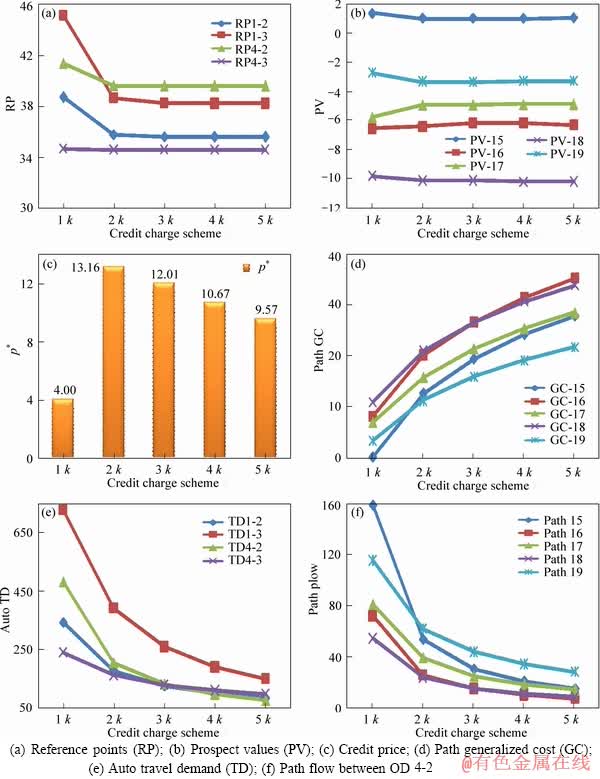
Figure 8 Comparison of solutions under different credit charge schemes k:
The classical Nguyen-Dupuis network is taken as the test network to illustrate the proposed model and algorithm. The numerical results show that: 1) The ME credit price and reference points increase, with the on-time arrival probability increasing. However, the generalized path travel costs don’t increase necessarily. 2) With path-choice dispersion parameter θ increasing, the ME credit price and reference points may increase or decrease. When θ is great enough, CPT-based SUE path flow becomes equal to CPT-based UE path flow. 3) The mode-split dispersion parameter 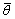 has very little influence on the reference points and PV. However, the travel demands in road sub-network, as well as the ME credit price, are influenced by
has very little influence on the reference points and PV. However, the travel demands in road sub-network, as well as the ME credit price, are influenced by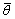 to a large extent. 4) The reference points and PV change little under different TC rates, but the ME credit price decreases with the increasing of TC rates of buying credit ρb, while it increases with the increasing of TC rates of selling credit ρs. 5) With the credit charges k increasing, more travel demands in road sub-network would transfer to the metro mode, which indicates that TCS is promising in improving service level of multimodal transportation system.
to a large extent. 4) The reference points and PV change little under different TC rates, but the ME credit price decreases with the increasing of TC rates of buying credit ρb, while it increases with the increasing of TC rates of selling credit ρs. 5) With the credit charges k increasing, more travel demands in road sub-network would transfer to the metro mode, which indicates that TCS is promising in improving service level of multimodal transportation system.
For future research, the multiclass travelers with heterogeneous risk attitudes can be considered to extend this study. And the optimal TCS design problem based on the proposed traffic equilibrium model in this paper can also be further investigated. Besides, some further studies under more practical assumptions are worthy of devoting effort, such as considering park and ride choice behavior, route choice in large metro sub-network, transfer behavior between different metro lines, and so on.
Nomenclature
G
A general strongly connected road network
G′
Rail network
N
Set of nodes
N′
Set of nodes on the rail network
A
Set of directed links, a∈A
A′
Directed links on the rail network
W
Set of O-D pairs, w∈W
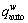
Traffic demand on road network for O-D pair, w∈W
Rw
Set of all paths between O-D pair, w∈W
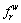
Flow on path, r∈Rw
va
Flow on link, a∈A
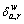
Element of the link/path incidence matrix
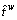
Travel time on metro line between O-D pair, w∈W

Fare on metro line between O-D pair, w∈W
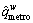
Traffic demand on rail network for O-D pair, w∈W
K
Total amount of credits issued
fw
Initial credit amount distributed to each traveler between O-D pair, w∈W
ka
Credit charges on link, a∈A
k
Credit charge scheme on road network, k=[ka, a∈A]
ta
Mean travel time on link, a∈A
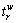
Path travel time on route, r∈Rw
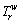
Random path travel time on path, r∈Rw
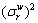
Variance of path travel time on path, r∈Rw
ζ
Lower limit of travelers’ desired on-time arrival probability
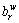
The minimal budgeted time for taking path, r∈Rw

Path-travel-time reference point between O-D pair, w∈W
gw(·)
Value function
Ψ(φ)
Perceived probability of an event
φ
Actual probability of an event

Time prospect value for choosing path, r∈Rw
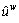
Time prospect values on the metro line between O-D pair, w∈W
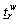
Lower bounds of the travel time on path,r∈Rw
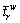
Upper bounds of the travel time on path,r∈Rw
ρs
TC rate of selling credits, ρs∈[0, 1]
ρb
TC rate of buying credits, ρb∈[0, 1]
p
Credit price measured in money unit
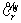
Perceived generalized travel cost on path, r∈Rw
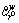
Expected generalized travel cost on path,r∈Rw
κ
Conversion coefficient between time PV and monetary cost
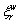
Traveler’s perception error of road sub-network
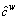
Expected generalized travel cost on metro line between O-D pair, w∈W

Traveler’s perception error of rail sub-network
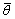
Dispersion parameter of mode choice
θ
Dispersion parameter of route choice
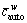
Weighted average of the expected generalized path costs between O-D pair,w∈W

Choice probability of the path, r∈Rw evaluated at 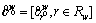
λw
Exogenous attractiveness of metro line between O-D pair, w∈W
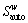
Satisfaction function between O-D pair,w∈W
References
[1] YANG H, WANG X L. Managing network mobility with tradable credits [J]. Transportation Research Part B, 2011, 45(3): 580-594. DOI: 10.1016/j.trb.2010.10.002.
[2] WU D, YIN Y, LAWPHONGPANICH S, YANG H. Design of more equitable congestion pricing and tradable credit schemes for multimodal transportation networks [J]. Transportation Research Part B, 2012, 46(9): 1273-1287. DOI: 10.1016/j.trb.2012.05.004.
[3] AKAMATSU T, WADA K. Tradable network permits: A new scheme for the most efficient use of network capacity [J]. Transportation Research Part C: Emerging Technologies, 2017, 79: 178-195. DOI: 10.1016/j.trc.2017.03.009.
[4] NIE Y, YIN Y. Managing rush hour travel choices with tradable credits scheme [J]. Transportation Research Part B, 2013, 50(4): 1-19. DOI: 10.1016/j.trb.2013.01.004.
[5] TIAN L J, YANG H, HUANG H J. Tradable credits schemes for managing bottleneck congestion and modal split with heterogeneous users [J]. Transportation Research Part E, 2013, 54(8): 1-13. DOI: 10.1016/j.tre.2013.04.002.
[6] XIAO F, QIAN Z, ZHANG H M. Managing bottleneck congestion with tradable credits [J]. Transportation Research Part B, 2013, 56: 1-14. DOI: 10.1016/j.trb.2013.06.016.
[7] XIAO L L, LIU T L, HUANG H J. Tradable permit schemes for managing morning commute with carpool under parking space constraint [J]. Transportation, 2019, 46(1): 1-24. DOI: 10.1007/s11116-019-09982-w.
[8] XU M, WANG G, GRANT-MULLER, GAO Z. Joint road toll pricing and capacity development in discrete transport network design problem [J]. Transportation, 2017, 44: 1-22. DOI: 10.1007/s11116- 015-9674-2.
[9] WANG G, GAO Z, XU M. Integrating link-based discrete credit charging scheme into discrete network design problem [J]. European Journal of Operational Research, 2019, 272(1): 176-187. DOI: 10.1016/j.ejor.2018.05.069.
[10] WANG G, XU M, GRANT-MULLER S, GAO Z. Combination of tradable credit scheme and link capacity improvement to balance economic growth and environmental management in sustainable-oriented transport development: A bi-objective bi-level programming approach [J]. Transportation Research Part A: Policy and Practice, 2018. DOI: 10.1016/j.tra.2018. 10.031.
[11] LI Y, UKKUSURI S V, FAN J. Managing congestion and emissions in transportation networks with dynamic carbon credit charge scheme [J]. Computers & Operations Research, 2018, 99: 90-108. DOI: 10.1016/j.cor.2018.06.014.
[12] HAN F, CHENG L. Stochastic user equilibrium model with a tradable credit scheme and application in maximizing network reserve capacity [J]. Engineering Optimization, 2017, 49(4): 549-564. DOI: 10.1080/0305215X.2016. 1193357.
[13] WANG X L, YANG H, ZHU D L, LI C. Tradable travel credits for congestion management with heterogeneous users [J]. Transportation Research Part E, 2012, 48(2): 426-437. DOI: 10.1016/j.tre.2011.10.007.
[14] ZHU D L, YANG H, LI C M, WANG X L. Properties of the multiclass traffic network equilibria under a tradable credit scheme [J]. Transportation Science, 2015, 49(3): 519-534. DOI: 10.1287/trsc.2013.0508.
[15] LIU Y, NIE Y M. A credit-based congestion management scheme in general two-mode networks with multiclass users [J]. Networks and Spatial Economics, 2017, 17(3): 681-711. DOI: 10.1007/s11067-017-9340-7.
[16] WANG J P, LIU T L, HUANG H J. Tradable OD-based travel permits for bi-modal traffic management with heterogeneous users [J]. Transportation Research Part E: Logistics and Transportation Review, 2018, 118: 589-605. DOI: 10.1016/j.tre.2018.08.015.
[17] NIE Y. Transaction costs and tradable mobility credits [J]. Transportation Research Part B, 2012, 46(1): 189-203. DOI: 10.1016/j.trb.2011.10.002.
[18] BAO Y, GAO Z, XU M, YANG H. Tradable credit scheme for mobility management considering travelers’ loss aversion [J]. Transportation Research Part E, 2014, 68: 138-154. DOI: 10.1016/j.tre.2014.05.007.
[19] HE F, YIN Y F, SHIRMOHAMMADI N, NIE Y M. Tradable credit schemes on networks with mixed equilibrium behaviors [J]. Transportation Research Part B, 2013, 57: 47-65. DOI: 10.1016/j.trb.2013. 08.016.
[20] GUO R Y, HUANG H J, YANG H. Tradable credit scheme for control of evolutionary traffic flows to system optimum: Model and its convergence [J]. Networks and Spatial Economics, 2019, 19(3): 833-868. DOI: 10.1007/s11067- 018-9432-z.
[21] XIAO F, LONG J, LI L, KOU G, NIE Y. Promoting social equity with cyclic tradable credits [J]. Transportation Research Part B: Methodological, 2019, 121: 56-73. DOI: 10.1016/j.trb.2019. 01.002.
[22] DOGTEROM N, ETTEMA D, DIJST M. Tradable credits for managing car travel: A review of empirical research and relevant behavioural approaches [J]. Transport Reviews, 2017. DOI: 10.1080/01441647.2016.1245219.
[23] YIN Y, IEDA H. Assessing performance reliability of road networks under non-recurrent congestion [J]. Transportation Research Record, 2001, 1771: 148-155. DOI: 10.3141/1771- 19.
[24] LO H K, LUO X W, SIU B W Y. Degradable transport network: Travel time budget of travelers with heterogeneous risk aversion [J]. Transportation Research Part B, 2006, 40(9): 792-806. DOI: 10.1016/j.trb.2005.10.003.
[25] SHAO H, LAM W H K, TAM M L. A reliability-based stochastic assignment model for network with multiple user classes under uncertainty in demand [J]. Network and Spatial Economics, 2006, 6(3, 4): 173-204. DOI: 10.1007/s11067- 006-9279-6.
[26] SUN C, CHENG L, ZHU S, HAN F, CHU Z. Multi-criteria user equilibrium model considering travel time, travel time reliability and distance [J]. Transportation Research Part D, 2019. DOI: 10.1016/j.trd. 2017.03.002.
[27] WATLING D. User equilibrium traffic network assignment with stochastic travel times and late arrival penalty [J]. European Journal of Operational Research, 2006, 175(3): 1539-1556. DOI: 10.1016/j.ejor.2005.02.039.
[28] ZHOU Z, CHEN A. Comparative analysis of three user equilibrium models under stochastic demand [J]. Journal of Advanced Transportation, 2008, 42(3): 239-263. DOI: 10.1002/atr.5670420304.
[29] AVINERI E. The effect of reference point on stochastic network equilibrium [J]. Transportation Science, 2006, 40(4): 409-420. DOI: 10.2307/25769318.
[30] CONNORS R D, SUMALEE A. A network equilibrium model with travelers’ perception of stochastic travel times [J]. Transportation Research Part B, 2009, 43(6): 614-624. DOI: 10.1016/j.trb.2008.12.002.
[31] XU H, LOU Y, YIN Y, ZHOU J. A prospect-based user equilibrium model with endogenous reference points and its application in congestion pricing [J]. Transportation Research Part B, 2011, 45(2): 311-328. DOI: 10.1016/j.trb. 2010.09.003.
[32] SUMALEE A, CONNORS R D, LUATHEP P. Network equilibrium under cumulative prospect theory and endogenous stochastic demand and supply [C]// Transportation and Traffic Theory 2009: Golden Jubilee. Boston, MA: Springer, 2009: 19-38. DOI: 10.1007/978- 1-4419-0820-9_2.
[33] KOSZEGI B, RABIN M. A model of reference-dependent preferences [J]. Quarterly Journal of Economics, 2006, 121(4): 1133-1165. DOI: 10.1093/qje/121.4.1133.
[34] PRELEC D. The probability weighting function [J]. Econometrica, 1998, 66(3): 497-527. DOI: 10.2307/ 2998573.
[35] TVERSKY A, KAHNEMAN D. Advances in prospect theory: Cumulative representation of uncertainty [J]. Journal of Risk and Uncertainty, 1992, 5(4): 297-323. DOI: 10.2307/41755005.
[36] XU X, CHEN A, JANSUWAN S, YANG C, RYU S. Transportation network redundancy: Complementary measures and computational methods [J]. Transportation Research Part B, 2018, 114: 68-85. DOI: 10.1016/j.trb.2018.05.014.
[37] MENG Q, LIU Z. Impact analysis of cordon-based congestion pricing on mode-split for a bimodal transportation network [J]. Transportation Research Part C, 2012, 21(1): 134-147. DOI: 10.1016/j.trc.2011.06.007.
[38] WU Z X, LAM W H K, HUANGH J. Equity and efficiency analysis of pricing strategies in a bimodal network with heterogeneous user groups [J]. Transportation Research Record, 2008, 2089: 43-50. DOI: 10.3141/2089-06.
[39] CANTARELLA G E. A general fixed-point approach to multimode multi-user equilibrium assignment with elastic demand [J]. Transportation Science, 1997, 31(2): 107-128. DOI: 10.1287/trsc.31.2.107.
[40] MENG Q, LIU Z, WANG S. Asymmetric stochastic user equilibrium problem with elastic demand and link capacity constraints [J]. Transportmetrica A: Transport Science, 2014, 10(4): 304-326. DOI: 10.1080/23249935.2013.765929.
[41] FACCHINEI F, PANG J. Finite-dimensional variational inequalities and complementarity problems [M]. New York: Springer-Verlag, 2003. DOI: 10.1007/b97544.
(Edited by HE Yun-bin)
中文导读
可交易路票策略下的双模式随机网络交通分配问题:累积前景理论方法
摘要:本文研究了可交易路票策略(Tradable Credit Scheme, TCS)下双模式随机网络中的交通均衡配流问题。采用累积前景理论(Cumulative Prospect Theory, CPT)来描述出行者在不确定环境下的风险决策行为。假设出行者选择理解的广义路径费用(包括时间前景值和货币费用)最小的路径进行出行。在给定路票策略下的交通均衡状态,内生的参考点和路票价格保持不变,而且与道路子网络中的均衡流量形态和对应的出行时间概率分布一致。为了描述这种交通均衡状态,本文构建了路票策略下基于CPT的随机用户均衡(Stochastic User Equilibrium, SUE)条件。然后,建立了一个嵌套参数型不动点(Fixed Point, FP)模型的等价变分不等式(Variational Inequality, VI)模型,并在理论上分析了该模型的相关特性。本文设计了一种启发式算法来求解该模型,该算法包含两层迭代过程。其中,外层迭代是一个基于二分的收缩算法,用于寻找均衡路票价格;内层迭代本质上是相继平均算法(Method of Successive Averages, MSA),用于确定对应的基于CPT的SUE网络流量形态。通过数值实验,本文验证了模型和算法的正确性和有效性。
关键词:可交易路票;累积前景理论;内生参考点;广义路径费用;随机用户均衡;变分不等式模型;启发式算法
Foundation item: Project(BX20180268) supported by National Postdoctoral Program for Innovative Talent, China; Project(300102228101) supported by Fundamental Research Funds for the Central Universities of China; Project(51578150) supported by the National Natural Science Foundation of China; Project(18YJCZH130) supported by the Humanities and Social Science Project of Chinese Ministry of Education
Received date: 2018-10-10; Accepted date: 2019-08-02
Corresponding author: HAN Fei, PhD, Lecturer; Tel: +86-13572187796; E-mail: hanfei@chd.edu.cn; ORCID: 0000-0003-4987-2638
Abstract: The traffic equilibrium assignment problem under tradable credit scheme (TCS) in a bi-modal stochastic transportation network is investigated in this paper. To describe traveler’s risk-taking behaviors under uncertainty, the cumulative prospect theory (CPT) is adopted. Travelers are assumed to choose the paths with the minimum perceived generalized path costs, consisting of time prospect value (PV) and monetary cost. At equilibrium with a given TCS, the endogenous reference points and credit price remain constant, and are consistent with the equilibrium flow pattern and the corresponding travel time distributions of road sub-network. To describe such an equilibrium state, the CPT-based stochastic user equilibrium (SUE) conditions can be formulated under TCS. An equivalent variational inequality (VI) model embedding a parameterized fixed point (FP) model is then established, with its properties analyzed theoretically. A heuristic solution algorithm is developed to solve the model, which contains two-layer iterations. The outer iteration is a bisection-based contraction method to find the equilibrium credit price, and the inner iteration is essentially the method of successive averages (MSA) to determine the corresponding CPT-based SUE network flow pattern. Numerical experiments are provided to validate the model and algorithm.


