三维频率域可控源电磁法有限元-无限元结合数值模拟-有色金属在线

频率域可控源电磁法有限元数值模拟数据量大、耗费时间长的问题，引入无限单元来取代施加在外边界上的人工边界条件。电磁场在无限单元内扩散至无限远处，并最终衰减为0。由此，有限元剖分区域的范围被大幅减小，总自由度数相应降低，计算速度随之加快。数值模拟结果表明：采用本文提出的有限元-无限远结合算法后，有限元网格化区域不到原先的1%，自由度总数减少约33%，求解时间节省约25%，计算精度与大范围下施加Dirichlet外边界条件的有限元结果相当。

关键词：

三维；可控源电磁法；有限元；无限元；

中图分类号：P319.1⁺2 文献标志码：A 文章编号：1672-7207(2014)04-1251-10

3D frequency domain controlled source electromagnetic numerical modeling with coupled finite-infinite element method

TANG Jingtian, ZHANG Lincheng, GONG Jinzhe, XIAO Xiao

(Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education,

School of Info-physics and Geomatics Engineering, Central South University, Changsha 410083, China)

Abstract: Due to the large scale of the survey domain, the three dimensional (3D) controlled source electromagnetic (CSEM) numerical modeling usually brings about large amount of data and is very time consuming. To solve these problems, in this study, infinite elements were introduced into the finite element analysis to substitute the conventional artificial boundary conditions, which made the electromagnetic fields diffuse to infinity and attenuate to 0. As a result, the discretization domain for finite elements, as well as the total number of degrees of freedoms and time consumption, can be reduced remarkably. The numerical tests show that with the finite-infinite element coupling algorithm, the finite elements discretization domain is less than 1% of the conventional finite element modeling. The total numbers of freedom degrees are reduced around 33%, and time consumptions are saved around 25% while the accuracy is equal.

Key words: 3D; controlled source electromagnetic; finite element; infinite element

可控源电磁法(Controlled source electromagnetic method，CSEM)是20世纪70年代提出并被应用到地球物理领域，在矿产普查，油气勘探，水文环境等各个方面发挥了巨大的作用。该方法是利用两端接地的有限长导线作为电偶极源，或者利用水平放置的线圈作为磁发射源，使用人工交流电源激发交变电磁场，在地表观测电磁响应并计算波阻抗以及视电阻率进行勘探的一种方法。相对于传统的大地电磁勘探方法，由于可控源电磁法具有信号强、分辨率高的特点^[1-2]，该方法在2 km以内的表层勘探中得到了广泛应用，且近些年海洋可控源电磁法也得到了迅猛发展。由于解析法只能计算简单模型，数值模拟已成为计算较复杂模型中可控源电磁法响应的主要手段。电磁分布边值问题的数值计算方法包括有限差分法、积分方程法、有限单元法和边界单元法等4种基本类型。其中，有限单元法由于网格可控、精度较高，在电磁法正演领域更具优势。受限于计算技术的制约，以往的研究大都局限于2维或2.5维问题^[3-8]。近年来，随着计算机技术的飞速发展，三维电磁法数值模拟已可以在个人电脑上实现，相关研究也逐渐增多。其中，Mitsuhata等^[9]采用T-Ω有限元方法，把节点元和棱边元结合起来，模拟了三维大地电磁场。国内，闫述^[10]对三维频率域可控源电磁法数值模拟进行了较多研究，但主要基于矢量有限元，模型也较为简单。张继峰^[11]实现了基于电场双旋度方程的三维可控源电磁法有限单元法数值模拟，但受限于方程组存储和求解技术的制约，网格最大剖分数量有限。总体而言，三维可控源电磁法数值模拟还处在发展阶段，面临的主要问题包括源和边界条件的加载以及如何提高计算速度，减少数据存储量。由于三维模拟中场源存在奇异性，会使得最终的大型复系数线性方程组的求解，特别是迭代法求解，存在不稳定性。目前处理办法主要包括Mitsuhata等^[5]采用的伪delta函数(pseudo–delta function)法和闫述^[12]采用的近场值代替法。在外边界条件加载方面，常用的处理办法包括将有限元网格放置到很大范围，从而认为边界处电磁场已衰减为零，以及用均匀半空间下的远场值作为Dirichlet边界条件加载到边界结点上^[10-11]。后一种方案虽然使得网格化范围有所缩减，但仍要求外边界网格远离源和目标体，从而使得外边界上的节点满足远场条件，以及减少目标体散射场的影响。对于接近野外实际的三维模型，各个方向的外边界一般都要在几万米外，这就包含了大量的节点数。又由于电磁法中每个结点包含多个自由度，从而使得存储量巨大，计算十分耗时。为解决上述问题，本文采用了无限单元法^[12-13]取代传统的外边界条件。无限单元是某一方向延伸至无限远处的单元。它通过坐标映射函数与有限元网格结合，确定无限单元结点与有限单元结点的几何关系；借助特殊的形函数，使得电磁场在无限单元中按某一规律衰减，并在无限远处衰减至零。Blome等^[14]应用Astley无限元处理直流电法边界问题，缩小了计算范围，减少了节点数, 并且避免了采用Dirichlet或混合边界条件，但是其采用的无限元形函数较为复杂，且由于引入了Astley无限元中特有的额外权重因子，使整体系数矩阵失去了对称性。Towers等^[15^-16]借助无限元研究了基于Helmholtz方程的二维电磁场散射问题；Gratkowsk等^[17-18]将无限元与标量有限元结合解决三维电磁场问题，但是，其采用的无限元形函数较为复杂。Cecot等^[19]在三维电磁法hp自适应有限元数值模拟中做了大量研究，并成功地将无限单元法与矢量有限元法相结合，但其研究的问题的范围通常较小，且没有在地球物理电磁法领域中应用。国内，李培芳^[20]简单探讨了无限元在电磁场计算中的应用；汪金山等^[21]研究了二维稳态电磁场数值计算中的无限单元法；孙跃^[22]提出了用有限元、无限元相结合来计算三维稳定电流场的方法，效果优于Dirichlet边界条件，但仅给出了基于六面体单元的基本公式和简单结果，对无限元映射函数和形函数均未作详细说明。在本文中，首先实现了基于电场双旋度方程的三维频率域可控源电磁法标量有限元数值模拟。场源加载方面，采用了近场值代替法。外边界条件方面，采用无限单元取代了人工边界条件，并提出了一种新的无限元形函数^[23]。它基于Lagrange插值多项式和某一修正系数^[24]的乘积，其在三维直流电法和三维可控源电磁法数值模拟中均可用于模拟电场或电磁场的衰减，从而有效缩减有限单元离散的范围。数值计算表明：仅在几千米的有限元离散范围情况下，本文作者提出的有限元-无限元结合算法即可达到与传统的基于Dirichlet边界条件的算法相同的计算精度，计算时间和数据存储量可节约30%。

1 三维CSAMT边值问题

1.1 基于电场分量的变分方程

对于水平电偶极子简谐源(时间因子e^-ⁱ^ωt)，其在均匀、线性、各向同性的导电介质中，产生的场满足的Maxell方程组为：

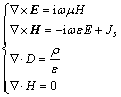(1)

其中：ω为角频率；σ为电阻率；J_s为场源电流密度,对方程组(1)第一式求旋度，将第二式代入第一式可得三维CSAMT中基于电场的双旋度方程^[13]：

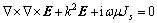(2)

其中：k为波数，准静态极限下k²=iωμσ，利用广义变分原理可得式(2)的泛函^[11]：

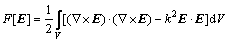(3)

式(3)即为有限元及其有限元与无限元耦合法进行CSMAT三维正演模拟的基本公式。

在三维高频电磁法有限元模拟中对伪解问题有比较多的讨论，在利用有限元来进行模拟时，由于离散化时只对插值函数的连续性做了要求，对其导数未做任何要求，这样有限元求得解往往会产生伪解(非物理解)，研究表明主要是有限元解不满足散度条件^[11]，即对于磁场来说，不满足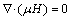；而对于电场来说，不满足。

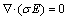对于式(3)的求解，在式中增加一罚项，介质和空气中都加入散度条件^[11]：

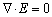
则电场变分方程变为

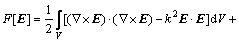
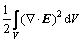(4)

1.2 边界条件及源的加载

CSAMT中由于人工源的引入，使得可控源测量时有近区和远区之分，因此，在进行数值模拟时源和外边界条件的加载就变的极其复杂，在远区时电磁波的传播满足平面波，近区时为非平面波，其传播规律不同。所以，需针对不同的情况加载源和边界条件。

在有限元数值模拟中，对于边界条件往往采用的是Dirichlet边界条件，要求外边界足够远，一般为几千米或数十千米，从而可以认为是无穷远，这时采用均匀半空间远区表达式，将其转换为区域外边界条件加载到远区各个节点上^[10]，具体表达式如下。

空中远处：

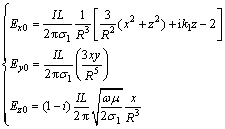(5)

地下远处：

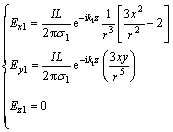(6)

采用Dirichlet边界条件，一方面忽略了地下目标体对电磁波传播的影响，另一方面它为保证有限元解的精度，要求边界足够大，从而大大扩大了非研究区域，带来大量多余的有限元网格，使得节点数和自由度增加，加大了正演模拟时计算机所占用的内存，延缓了计算速度。

对于源的加载，一种是采用伪delta函数，利用一个小区域来代替点源，消除源的奇异性；另一种是将均匀半空间下电场的近场值加载到场源附近的节点上^[10]。近场电场各个分量的表达式如下。

空气中：

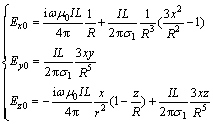(7)

地下围岩：

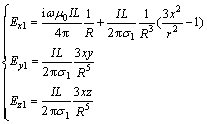(8)

式中：I为电流；L为偶极距；σ₁为地下背景电导率；r和R分别为目标结点到坐标原点的水平距离(在x-y平面)和三维直线距离。在本文采用将均匀半空间下电场近场值加载到场源附近的结点上的方案。

2 有限元网格划分

在三维CSAMT有限元数值模拟中，将研究区域分为目标区域和边界区域，目标区域含源，测点, 目标体，采用六面体，八节点有限元网格划分^[11]，如图1所示。

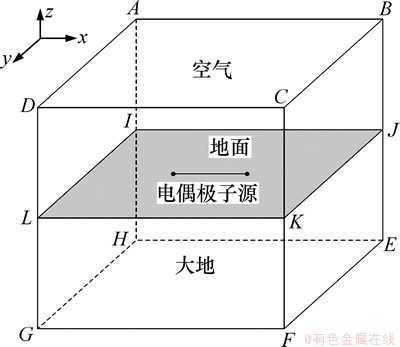
图1 三维CSAMT模型示意图

Fig. 1 3D CSMT model

图2所示为网格划分示意图。从图2可以看出：在目标区域，为保证其正演模拟时解的准确度和精度，网格划分众多，网格尺度小；在边界区域，网格划分比较粗糙，网格尺度大，采用尺度向外逐渐变大的划分方法。

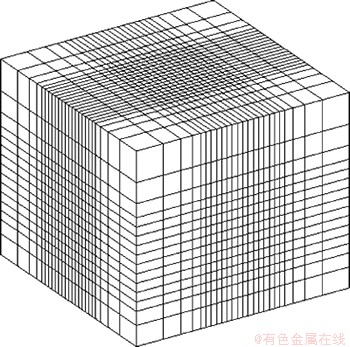
图2 网格剖分示意图

Fig. 2 Mesh geometry

3 有限元与无限元耦合

无限元法基本思想是引入一种几何上无限大的“有限”单元，然后对其在物理上进行界定。无限元是为克服有限元在解决无穷远边界问题时而提出，是对有限元方法的一种补充，因而通过无限元与有限元的耦合，可以很完美的处理无穷远边界问题。

采用有限元与无限元耦合法来处理三维CSAMT边界条件时，一方面可以保证无穷远处电场场值衰减为零，真正意义上处理外边界条件，另一方面，通过无限元映射可以缩减有限元的计算区域，减少有限元网格，加快计算速度。

3.1 无限元要素

图3所示为一典型的二维“四边形”无限单元，1，2，3和4这4个节点即为这个无限元几何形状的基本要素。

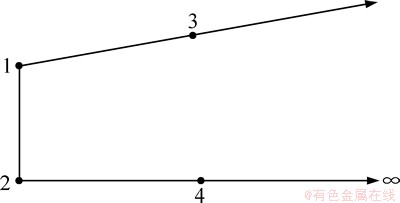
图3 二维无限单元及其要素

Fig. 3 Factors of 2D infinite element

图3中，1和2连线为二维无限元边界，1和2为无限元的节点，3和4为无限元中间节点，1，3连线和2，4连线为无限单元的边。无限单元比较简单，两条边1，3和2，4在坐标系中始终保持为直线，利用两条连线可以描述无限单元的几何特征，并且无限单元通过它的2条边与相邻的无限单元或趋于无限的边界相连。

无限元与有限元的主要区别是，无限单元具有方向性，1，2，3和4这4个节点在坐标系中顺序是固定的，并且无限单元的两条边在无穷远处不能相交。

3.2 无限元映射

采用的无限元为astley无限元^{[12-13, 24]}。无限元与有限元耦合，就是说在传统有限元离散区域的外边界至无限远这个方向，采用无限元映射和形函数，将整体坐标映射到局部坐标上来，以此来代替传统的有限元边界条件，从而克服传统有限元网格剖分要求边界足够远的条件，大大缩减边界区域范围，减少自由度数和加快计算速度。一维情况下的映射原理如图4所示。

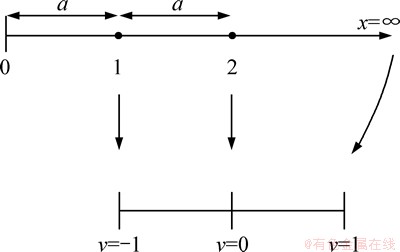
图4 无限元一维映射示意图

Fig. 4 1-D infinite element mapping

映射无限单元，采用了2种函数：映射函数和形函数。图4中为一沿x轴方向趋于无穷远的一维无限元，单元由节点1通过节点2，延伸到无穷远，通过映射函数将整体坐标下的无限单元映射为一有限区域(-1，1)单元，即自然坐标下(-1，1)的母单元。

整体坐标和自然坐标之间的变换关系为

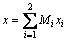(9)

其中：M_i为映射函数，

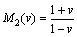， (10)

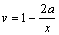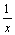这种映射具备唯一性，并且在二维和三维情况下均适用。由式(9)和(10)可以得到，表明v呈型衰减。

将一维情况应用到三维情况中，同样适用。图5中映射原点P为所有无限单元的映射出发点，一般可取在上表面的中心点处。以P点为原点，经过有限单元在外边界上的四边形的4个顶点，向外引出4条射线，形成无限单元的几何形式。点P到中间节点5，6，7和8的距离分别为点P到节点1，2，3和4的距离的2倍。在无限远处还有无限单元的4个节点，它们使得场值分布扩展到无限远处，但由于无限远处电场值位为0，故此四点不参与插值运算，因此，也就没有必要考虑。在局部坐标中，无限单元被映射为一个有限大小的四棱柱，从而可以进行积分运算。其中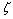方向表示无限远方向，其映射方式与上述的一维无限单元映射方式相同；在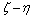平面内，无限单元与有限单元采用相同的映射形式和形函数。

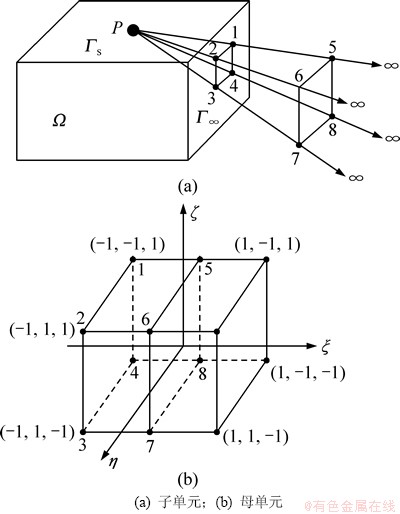
图5 无限元三维映射示意图

Fig. 5 3-D infinite element mapping

坐标映射为

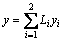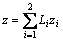， (11)

其中：L_i为四边形面积。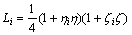

再结合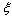方向的坐标映射关系式，得到8个节点无限单元的结点坐标映射函数：

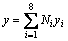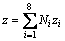，， (12)

其中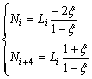：，i=1，2，3，4，即三角形面单元映射和面积坐标线性插值。

3.3 无限元形函数

在此，采用了在三维直流电法数值模拟中有比较好效果的一类无限元形函数作为无限元形函数，其具体表达式如下：

；i=1，2，3，4 (13)

该形函数由Astley映射无限单元理论中采用的形函数中的系数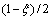与二阶Lagrange插值多项式的乘积。其与经典Astley映射无限单元理论不同，该无限元形函数一方面在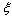方向使得电磁场沿此方向衰减至零，另一方面保持了系数矩阵的对称性，且构造简单，易于实现。

3.4 无限元分析

无限元是有限元的一种特殊情况，因此有限元与无限元单元分析基本一致，唯一不同的是无限元映射函数和形函数与有限元有所差别。有限元与无限元耦合法，网格都为八节点单元，因此在数值模拟中，可将无限元和有限元统一起来，从而使得求解简单、方便。

其中雅克比矩阵为

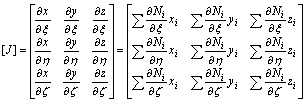(14)

整体坐标和局部坐标之间关系为

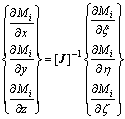(15)

4 方程组求解

有限元无限元耦合法最终形成的大型、稀疏、对称复系数方程组，由于网格单元多，自由度大，用普通的求解方法求解速度慢，耗用内存。在UBUNTU环境下，借助开源求解器PETSc，实现了复系数方程组的迭代法快速求解。实验表明：对于自由度约60万的问题，内存需求约为2.6 Gb，单频点整体运算时间约50 s，一般不超过1 min。

5 算例及分析

5.1 算例一：均匀半空间

均匀半空间模型，电阻率ρ为100 Ω·m，水平电偶极子AB长度为1 000 m，设计A(-500,0,0)，B(500,0,0),垂直收发距为5 100 m，测量区域为(-820, 5 100,0)到(820,5 100,0)。采用20个频点，具体为(单位Hz)：7 680，5 120，3 840，2 560，1 920，1 280，960，640，480，320，240，120，80，40，20，10，7.5，1.875和1.25。采用有限元-无限元耦合法，与均匀半空间解析解对比，其结果如图6所示。

与均匀半空间解析解结果相比，在远区和过渡区，即20~10 000 Hz之间，有限元-无限元耦合法模拟所得的视电阻率与解析解基本一致，相对误差E基本在4%以下，满足精度要求，但在近区，有限元无限元耦合法所得视电阻率值大于解析解，相对误差较大，这可能是由于三维数值模拟过程中，源的加载采用均匀半空间下电场的近场值加载到场源附近的结点上造成的。

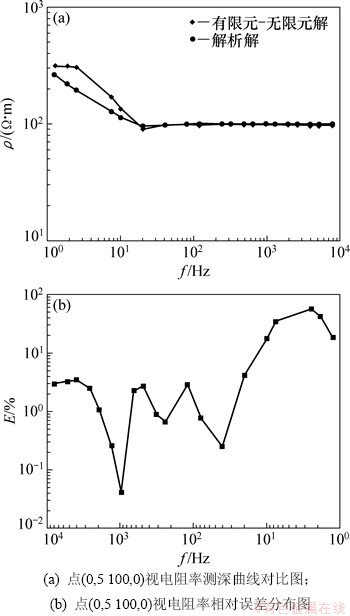
图6 测点视电阻率测深曲线图及误差分布图

Fig. 6 Curves of appear resistivity and misfit

5.2 算例二：高低阻组合体

采用均匀半空间下同时包含一个高阻目标体和一个低阻目标体的模型，分析对比了大区域的传统有限元的结果、小区域的有限元-无限元结合算法的结果以及小区域下仍使用Dirichlet外边界条件的结果。模型结构及部分参数如图7所示。

大地的背景电阻率为100 Ω·m，左边目标体电阻率为500 Ω·m，右边为10 Ω·m，目标体长×宽×高为600 m×400 m×200 m，埋深100 m。偶极距L=1 000 m，电流为1 A。频点为10~10 000 Hz，共41个，按对数坐标等距分布。

以大区域下传统有限元下的解为参考标准。大区域传统有限元离散化区域大小为：x方向对称分布长40 000 m，y方向长40 000 m，纵向z长为78 600 m，其中地下介质深度为27 400 m，3个方向的有限元节点数分别为86，53和42，其中在目标体和场源附近网格较密，靠近边界时网格间距逐渐放大。计算得到的Cagniard视电阻率按Bostick深度和频率分布的拟断面图如图8所示。

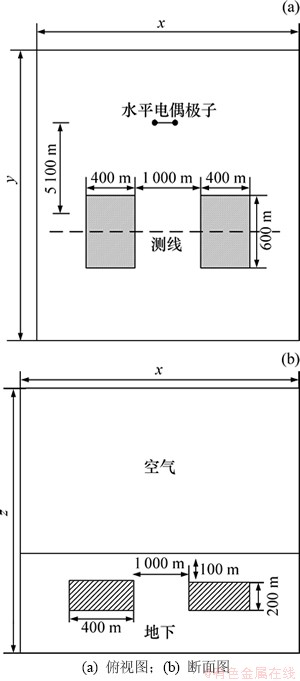
图7 均匀半空间下包含2个异常体模型

Fig. 7 Model with two anomalous bodies

借助无限单元法，边界区域的范围被极大缩减，此时x方向长为4 000 m；y方向长10 000 m，其中正方向，即目标体方向长度为7 000 m；z方向长5 600 m，其中空中距离为3 200 m。x，y和z 3个方向的有限元节点数分别为74，45和34。计算得到的Cagniard视电阻率按Bostick深度分布的拟断面图如图9所示。

利用与模型2相同的模型，使用施加Dirichlet外边界条件的传统有限元来对比。计算得到的Cagniard视电阻率按Bostick深度分布的拟断面图见图10。

为了便于对比，对于同种类型的拟断面图，采用相同的色标。由图8和图9可以看出：采用有限元-无限元算法的视电阻率拟断面图与大范围下传统有限元的结果十分相似，而在小区域时仍采用Dirichlet外边界条件则会得到畸变的图形，因为此时边界已不满足远场条件。

为了更精确地对比误差，以大范围下传统有限元的结果为参照，分别作了有限元-无限元结合法和小范围传统有限元法的相对误差分布拟断面图分别如图11和图12所示。

由于数值范围差距太大，已无法采用统一的色标。有限元-无限元结合法的相对误差不超过5%，有效频率内的相对误差不超过3%。小范围传统有限元法的最大相对误差达到了420%，出现在低阻目标体靠近外边界的一侧，充分说明了外边界对结果的影响；在有效频率范围内，其相对误差也达到了30%以上，且低频时的误差大于高频时的误差，靠近边界的误差大于中心处的误差。

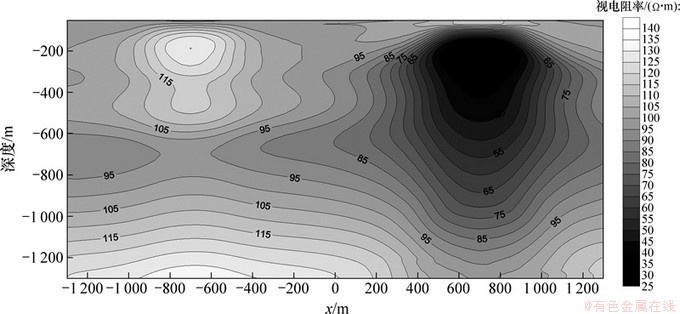
图8 大区域有限元法Cagniard视电阻率按Bostick深度拟断面图

Fig. 8 Cagniard apparent resistivity cross-section versus Bostick depth with finite element method in large domain

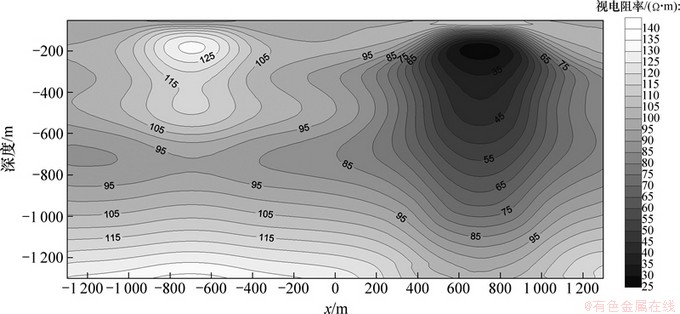
图9 有限元-无限元法Cagniard视电阻率按Bostick深度拟断面图

Fig. 9 Cagniard apparent resistivity cross-section versus Bostick depth with coupled finite-infinite element method

在保证计算精度的前提下，对比大范围下的有限元法，本文提出的有限元-无限元结合法可以极大减少自由度数和加快计算速度。表1对比了2种算法的

有限元区域大小、自由度总数和总计算时间。由表1可知：有限元-无限元结合法与传统有限元的计算区域、自由度总数和计算时间的比值分别为0.18%，66.53%和75.04%。

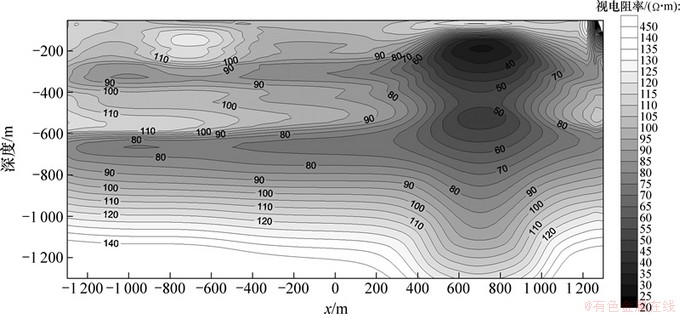
图10 小区域有限元Cagniard视电阻率按Bostick深度拟断面图

Fig. 10 Cagniard apparent resistivity cross-section versus Bostick depth with finite element method in small domain

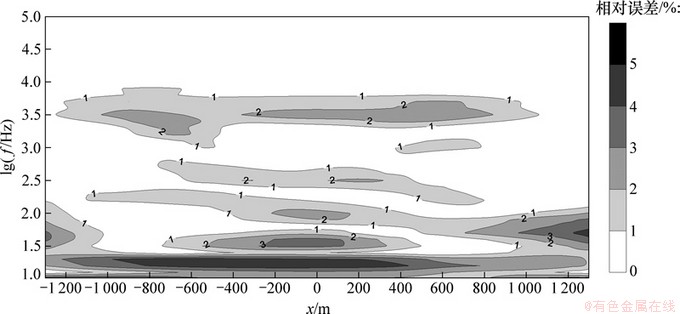
图11 有限元-无限元耦合法相对误差分布拟断面图

Fig. 11 Relative error cross-section for results of FEM-IEM coupling method

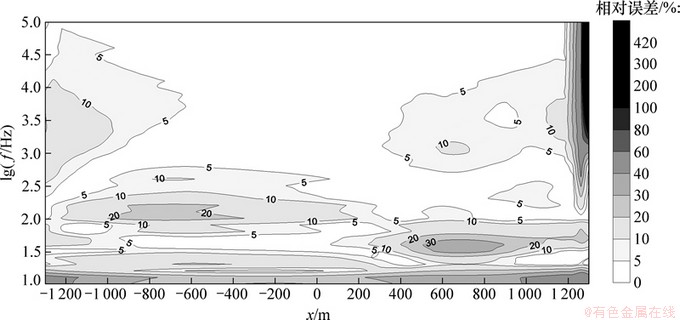
图12 小区域下传统有限元方法误差分布拟断面图

Fig. 12 Relative error cross-section for results of FEM method within small domain

表1 有限元-无限元结合法与传统有限元相关数据对比

Table 1 Comparision of FEM-IEM coupling method with conventional FEM method

6 结论

(1) 从频率域Maxwell方程组出发，得到了三维可控源电磁法的电场双旋度控制方程，并通过施加散度校正，克服了伪解的出现。基于六面体网格剖分，得到了有限元系数矩阵元素的具体表达式。通过将偶极子产生的近场解析电场值和远场解析电场值作为Dirichlet边界条件分别施加到场源附近的结点和外边界上的结点上，实现了三维频率域可控源电磁法标量有限元正演模拟。

(2) 推导了八节点无限单元的坐标映射函数和形函数，并将其与有限元网格相结合，取代外边界的Dirichlet边界条件。由此，有限元网格的剖分范围大大减少，节省了大量的自由度存储量和解方程运算时间。最后，通过数值模拟，与均匀半空间解析解进行对比，在过渡区和远区，有限元-无限元耦合法计算误差在4%以内，基本满足精度要求；并以大区域下传统有限元结果为参照，分析对比了本文提出的有限元-无限元结合法和在小区域情况下仍采用传统有限元法所得的结果。

(3) 本文提出的有限元-无限元结合法可以在较小的计算区域内得到与大剖分区域情况下传统有限元相同的计算精度，其自由度总数和运算时间仅为原方法的70%左右，而传统方法在相同的剖分区域范围内已不能得到令人满意的解。

参考文献：

[1] 汤井田, 何继善. 可控源音频大地电磁法及其应用[M]. 长沙: 中南大学出版社, 2005: 1-8.

TANG Jingtian, HE Jishan. Controlled source audio-frequency magnetotellurics and its application[M]. Changsha: Central South University Press, 2005: 1-8

[2] 何继善. 可控源音频大地电磁法[M]. 长沙: 中南工业大学出版社, 1990: 74-90.

HE Jishan. Controlled source audio-frequency magnetotellurics method[M]. Changsha: Central South University of Technology Press, 1990: 74-90.

[3] Lee K H, Morrison H F. A numerical solution for the electromagnetic scattering by a two-dimensional inhomogeneity[J]. Geophysics, 1985, 50(3): 466-472.

[4] Badea E A, Everettz M E, Newman G A, et al. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials[J]. Geophysics, 2001, 66(3): 786-799.

[5] Mitsuhata Y. 2-D electromagnetic modeling by the finite-element method with a dipole source and topography[J]. Geophysics, 2000, 65(2):465-475.

[6] Mitsuhata Y, Uchida T, Amano H. 2.5-D inversion of frequency-domain electromagnetic data generated by a grounded-wire source[J]. Geophysics, 2002, 67(6): 1753-1768.

[7] 底青云, Unsworth M, 王妙月. 复杂介质有限元法 2.5 维可控源音频大地电磁法数值模拟[J]. 地球物理学报, 2004, 47(4) :723-730.

DI Qingyun, Unsworth M, WANG Miaoyue. 2.5D CSAMT modeling with the finite element method over 2D complex earth media[J]. Chinese J Geophys, 2004, 47(4): 723-730.

[8] 底青云, Unsworth M, 王妙月. 有限元法2.5维CSAMT数值模拟[J]. 地球物理学进展, 2004, 19(2): 317-324.

DI Qingyun, Unsworth M, WANG Miaoyue. 2.5D CSAMT modeling with the finite element method[J]. Progress in Geophysics, 2004, 19(2): 317-324.

[9] Mitsuhata Y, Uchida Y. 3D magnetotelluric modeling using the T-Ω finite-element method[J]. Geophysics, 2004, 69(1): 108-119.

[10] 闫述. 基于三维有限元数值模拟的电和电磁探测研究[D]. 西安: 西安交通大学电子与信息工程学院, 2003: 55-60.

YAN Shu. Studies on the electromagnetic prospecting based on three-dimensional finite element method[D]. Xi’an: Xi’an Jiaotong University. School of Electronic and Information Engineering, 2003: 55-60.

[11] 张继峰. 基于电场双旋度方程的三维可控源电磁法有限单元法数值模拟[D]. 长沙: 中南大学信息物理工程学院, 2008: 83-107.

ZHANG Jifeng. Three dimensional controlled source electromagnetic numerical simulation based on electric field double curl equation using finite element method[D]. Changsha: Central South University. School of Information Physical Engineering, 2008: 83-107.

[12] Astley R J, Macaulay G. J. Mapped wave envelope elements for acoustical radiation and scattering[J]. Journal of Vibration and Acoustics, 1994, 170(1): 97-118.

[13] Astley R J, Macaulay G J, Coyette J P, et al. Three-dimensional wave-envelope elements of variable order for acoustic radiation and scattering. Part I: Formulation in the frequency domain[J]. The Journal of the Acoustical Society of America, 1998, 103(1): 49-63.

[14] Blome M, Maurer H R, Schmidt K. Advances in three-dimensional geoelectric forward solver techniques[J]. Geophys J Int, 2009, 176: 740-752.

[15] Towers M S, Mc Cowen A, Macnab J A R. Electromagnetic scattering from an arbitrary, inhomogeneous 2-D object-a finite and infinite element solution[J]. IEEE Transactions on Antennas and Propagation, 1993, 41(6): 770-777.

[16] Charles A, Towers M S, McCowen A. A general infinite element for terminating finite element meshes in electromagnetic scattering prediction[J]. IEEE Transactions on Magnetics, 1998, 34(5): 3367-3370.

[17] Gratkowski S, Ziolkowski M. A three-dimensional infinite element for modeling open-boundary field problems[J]. IEEE Transactions on Magnetics, 1992, 28(2): 1675-1678.

[18] Gratkowski S, Ziolkowski M. On the accuracy of a 3-D infinite element for open boundary electromagnetic field analysis[J]. Archivfur Elektrotechnik, 1994, 77: 77-83.

[19] Cecot W, Rachowicz W, Demkowicz L. An hp-adaptive finite element method for electromagnetics. Part 3: A three-dimensional infinite element for Maxwell’s equations[J]. International Journal for Numerical Methods in Engineering, 2003, 57: 899-921.

[20] 李培芳. 无限元在电磁场计算中的应用[J]. 电气应用, 1987(5): 1-3.

LI Peifang. The application of infinite element for calculating electromagnetic fields[J]. Electrotechnical Journal, 1987(5): 1-3.

[21] 汪金山, 李朗如. 二维稳态电磁场数值计算中的无限元方法[J]. 电工技术学报, 1996, 11(3): 56-59.

WANG Jinshan, LI langru. Infinite element method of computation of 2-D stationary electromagnetic field[J]. Transactions of China Electrotechnical Society, 1996, 11(3): 56-59.

[22] 孙跃. 直流电阻率法的三维有限元无限元数值分析[J]. 岩土工程学报, 2005, 27(7): 733-737.

SUN Yue. Numerical analysis for three-dimensional resistivity model by using finite element/infinite element methods[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(7): 733-737.

[23] 公劲喆. 有限元-无限元耦合法在三维直流电和电磁数值模拟中的应用[D]. 长沙: 中南大学信息物理工程学院, 2009: 34-37.

GONG Jinzhe. Application of finite-infinite element coupling method on 3D electric and electromagnetic numerical modeling[D]. Changsha: Central South University. School of Information Physical Engineering, 2009: 34-37.

[24] Astley R J, Coyette J P. Conditioning of infinite element schemes for wave problems[J]. Communications in Numerical Methods in Engineering, 2001, 17: 31-41.

(编辑杨幼平)

收稿日期：2013-05-25；修回日期：2013-09-10

基金项目：国家自然科学基金资助项目(41174105)；国家科技专项项目(SinoProbe 03-05)

通信作者：张林成(1986-)，男，河南许昌人，博士，从事CSAMT数值模拟研究；电话：0731-88877973；E-mail：cmm722@163.com

摘要：针对传统的三维频率域可控源电磁法有限元数值模拟数据量大、耗费时间长的问题，引入无限单元来取代施加在外边界上的人工边界条件。电磁场在无限单元内扩散至无限远处，并最终衰减为0。由此，有限元剖分区域的范围被大幅减小，总自由度数相应降低，计算速度随之加快。数值模拟结果表明：采用本文提出的有限元-无限远结合算法后，有限元网格化区域不到原先的1%，自由度总数减少约33%，求解时间节省约25%，计算精度与大范围下施加Dirichlet外边界条件的有限元结果相当。