时滞细胞神经网络的全局渐近稳定性和指数稳定性
张 发 明
(株洲工学院 信息与计算科学系,湖南 株洲,412008)
摘 要：
wer不动点定理,证明了具有变时滞的细胞神经网络模型平衡点的存在性;利用Barbarlet引理、Dini导数与导数之间的关系,构造了一个特殊的Lyapunov函数,表明具有变时滞的细胞神经网络模型存在惟一全局指数平衡点并且全局渐近稳定;在此基础上,通过构造一个新的M-矩阵,利用Halanay时滞微分不等式和M-矩阵的特性,得出:细胞神经网络模型在一定的条件下,在平衡点处,全局指数稳定且与时滞无关。
关键词: Lyapunov函数; 细胞神经网络; 渐近稳定性; 指数稳定性
中图分类号:O231.5 文献标识码:A 文章编号: 1672-7207(2005)01-0128-05
Globally Asymptotic Stability and Globally Exponential
Stability of a Class of Delayed Cellular Neural Networks
ZHANG Fa-ming
(Department of Information and Computing Science, Zhuzhou Institute of Technology, Zhuzhou 412008, China)
Abstract: Using Brouwer′s fixed theorem, the existence of the equilibrium point of a class of cellular neural networks model with time-varying delay is proved . Using Barbarlet′s lemma, the relationship between Dini′s derivative and derivative, a result is obtained that cellular neural networks model with time-varying delay has a unique globally exponential equilibrium point and a unique globally asymptotic stability by constructing a special kind of Lyapunov function, based on which it is proved that cellular neural networks model with time-varying delay has globally exponential stability at equilibrium point under a certain condition and has nothing to do with time delay by constructing a new M-matrix, using Halanay′s time delay differential inequality and the characteristic of the M-matrix.
Key words: Lyapunov function; cellular neural network; asymptotic stability; exponential stability
1988年,L.CHUA等提出了具有时延的细胞神经网络模型[1]:
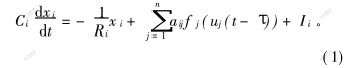
其中:
;C为电容;R为电阻;xi为电压;Ii为电流;ui为输入电压,|ui|≤1。
同时,L.CHUA等给出了实现的网络[1]。此种网络在图像信息的加工和处理中有着广泛的应用[2]。近年来,很多学者讨论了模型(1)的平衡点的存在性及全局渐近稳定性[3-6]。实际上,可变时滞细胞神经网络更为普遍,在动态变化过程中,绝对的常[CM(22] 时延很少,常数时延只不过是变时滞的一种理想化的近似,在很多情况下,只知道变滞量的界,并不知道其确切值。因此,对于可变时滞的细胞神经网络的研究,具有重要的理论意义和实用价值。
具有变时滞的细胞神经网络模型为:
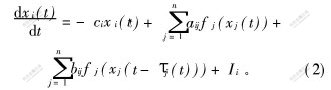
其中:i=1,2,…,n;n为神经网络中神经元的个数,n≥2;xi(t)为第i个神经元在t时刻的状态;ci,aij,bij和Ii是常数,且ci>0,fj(·):R→R,是非线性的激励函数;时滞τj(t)是t的函数,τ≥τj(t)≥0,τ是常数。假定:
(H1):fj(·):R→R,在R上有界(j=1,2,…,n)。
(H2):对于任意的x′∈R,x″∈R,必存在常数li>0,使得:|fi(x′)-fi(x″)|≤li|x′-x″|。其中:i=1,2,…,n。
易知fi(·)是R上的连续函数。
对具有变时滞的Hopfield型神经网络模型(2),在输出函数严格单调且连续可微的情况下,周冬明等从不同的角度以不同的方式讨论了平衡点的指数稳定性[7-12]。在此,作者利用Barbarlet引理、Halanay一维时滞微分不等式、Brouwer不动点定理和Lyapunov第二方法和Dini导数,讨论了具有变时滞的细胞神经网络模型(2)的平衡点的存在性、惟一性、渐近稳定性以及全局指数稳定性。
1 引 理
引理1(Barbarlet引理) 设g(·):[0,+∞)→R一致连续且g(·)∈L1[0,+∝),则
。
引理2[13] 设常数a>b>0,函数x(t)是在t0-τ上非负的一元连续函数,且在t≥t0上有如下的不等式成立:
(其中:
;τ≥0,为常数),则在t≥t0上,有:
。其中λ为超越方程λ=a-beλτ的惟一正根。
引理3[14] 设 C=(cij)(n×n)(n×n)和D=(dij)n×n是n阶实矩阵, y(t)是微分不等式
的解。其中:
,若cij≥0(i≠j),dij≥0,dij≥0,且-(C+D)是一个M矩阵,则存在常数λ>0,常向量k≥[AKy-D](0),使得对任意的t≥0,有y(t)≤ke-λt。
2 主要结果
定理1 对于神经元输出f(·)(i)(其中,i=1,2,…,n),若满足假定(H1)和(H2),则变时滞的细胞神经网络模型(2)必存在平衡点。
证明 如果 x*=(x*1,x*2,…,x*n)T是变时滞的细胞神经网络模型(2)的平衡点,那么,x*一定满足系统方程(2)。
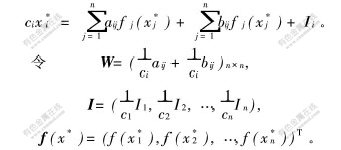
于是,上式可写成矩阵形式:
x*=P(x*)=Wf(x*)+I。
这样,x*就是P:Rn→Rn的不动点,利用Brouwer不动点定理可以证明映射P的不动点的存在性。事实上,P(x)的第i个分量满足:
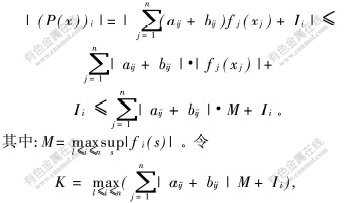
则P的值域为:
P(Rn)Q={(x1,x2,…,xn)∈Rn/|xi|≤K,
i=1,2,…,n}。
易见P是连续的,现把P限制在Q上,显然P/Q:Q→Q,即P/Q将Rn中的一个有界凸闭集Q映成本身,根据Brouwer 不动点定理知,P(x)至少有一个不动点。证毕。
定理2 对于变时滞的细胞神经网络模型(2),神经元输出f(·)(i)(其中,i=1,2,…,n)满足假定(H1)和(H2),如果
,则变时滞的细胞神经网络模型(2)存在惟一全局指数稳定平衡点且全局渐近稳定。
证明 设x*是系统(2)的平衡点,x(t)是系统(2)的异于x*的解,则
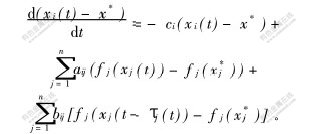
将上式两边同乘以符号函数sgn(xi(t)-x*i),可得:
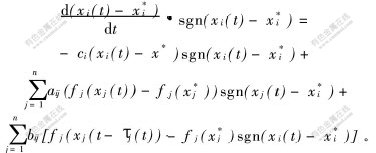
由Dini导数与导数之间的关系:
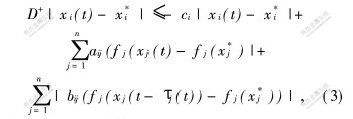
构造Lyapunov 函数:
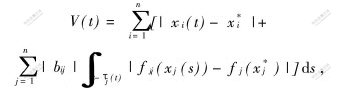
易知V(t)≥0。对V(t)求Dini导数并利用(3)式得:
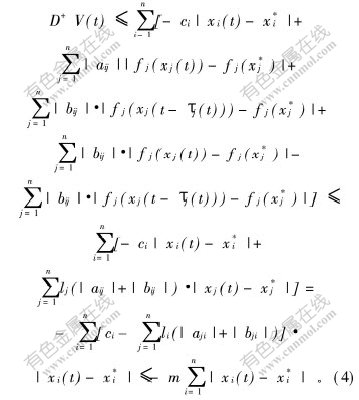
其中:
。对(4)式积分得:
在[0, +∞)上有界,不妨假设|xi(t)-x*i|≤M*(其中,t≥0, i=1,2,…,n),于是,有
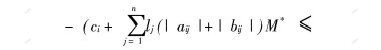
即D+(xi(t)-x*i)在[0,∞)上有界。所以,|xi(t)-x*i|在[0,∞)一致连续,从而
在[0,∞)上也一致连续,利用引理1,得
,即
。因为系统(2)的异于平衡点x*的任何解x(t),当t→∞时均趋于x*,并由(4)式知平衡点x*是稳定的,所以,变时滞的细胞神经网络模型(2)的平衡点是惟一的,并且是全局渐近稳定的。证毕。
定理3 对于变时滞的细胞神经网络模型(2),神经元输出fi(·)满足假定(H1)和(H2),若C—A—B是一个M-矩阵, 则变时滞的细胞神经网络模型(2)平衡点x*是全局指数稳定且与时滞无关。
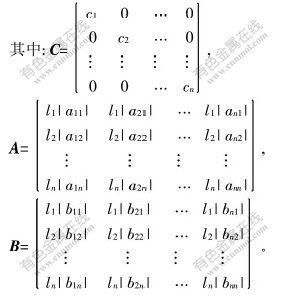
证明 设x*是系统(2)的平衡点,则
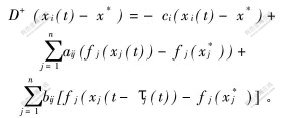
于是,有
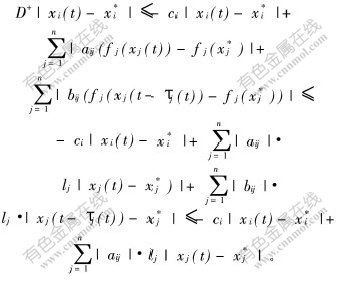
则有:
已知C-A-B是一个M-矩阵,根据引理3,存在常数λ>0,常向量k=(k1, k2, …, kn)T, 使得对任意的t≥0,有yi(t)≤kie-λt。
由定义知:变时滞的细胞神经网络模型(2)平衡点x*是全局指数稳定的,且与时滞无关。将本方法与文献[10]和[11]中的方法进行比较可知:
a. 采用矩阵的范数
来判断时滞细胞神经网络模型平衡点的存在性和指数稳定性,计算较繁杂[10];而采用本文方法不需要计算范数,只须判断C-A-B是否为M-矩阵,这种判断可以在计算机上完成,易于实现。
b. 文献[10]的结论仅针对于C=I这一特殊情况,有失一般性。这里将C扩展到对角矩阵,显然, 所讨论的时滞细胞神经网络模型更接近于实际设计系统,具有更好的适应性。
c. 文献[10]中,要求
, 导致对系统的要求很高。这里, 只须C-A-B是M-矩阵,就可判断时滞细胞神经网络模型的全局指数稳定性。因此, 采用该方法能判断更复杂的系统的指数稳定性。
d. 文献[11]中的结论引入了多个参数,只有取定适当的参数时,才能判断其指数稳定性,这样主观性很强。而采用本方法不需选择参数,易于操作。
3 应用实例
考虑时滞细胞神经网络模型:
由定理2知该系统存在惟一全局指数稳定平衡点,由定理3知该系统是全局指数稳定的,且与时滞无关。
4 结 论
a. 通过构造一个特殊的Lyapunov函数,可得出具有变时滞的细胞神经网络模型存在惟一全局指数平衡点并且全局渐近稳定。
b. 通过构造一个新的M-矩阵,证明在平衡点处全局指数稳定且与时滞无关。
c. 运用时滞细胞神经网络不需要计算矩阵范数,也不需要选取参数,判断系统的稳定性简单、易操作。
参考文献:
[1] CHUA L,YANG L. Cellular Neural Network: Theory[J]. IEEE TransCAS-I,1988,35(10):1257-1272.
[2]CHAO L,YANG L.Cellular Neural Network: Application[J]. IEEE Trans CAS-I, 1988, 35(10): 1273-1290.
[3]CAO Jin-de. Periodic Solutions and Exponential Stability in Delayed Cellular Networks[J]. Physical Review E ,1999;60:3244-3248.
[4]曹进德.具有时延的细胞神经网络的全局渐近稳定性分析[J].电子科学学刊,2000;22(2):253-259.
CAO Jin-de. Asymptotic Stability Analysis on Delayed Cellular Neural Networks[J]. Journal of Electronics ,2000,22(2):253-259.
[5]廖晓峰,吴中福,虞厥邦.时延的细胞神经网络的渐近稳定性条件[J].电子与信息学报,2001;23(1):45-51.
LIAO Xiao-feng, WU Zhong-fu, YU Jue-bang. Asymptotic Stability on Delayed Cellular Neural Networks[J]. Journal of Electronics and Information Technology, 2001,23(1):45-51.
[6]张发明. 时滞细胞神经网络的渐近稳定性[J]. 长沙交通学院学报, 2004,20(2):7-9.
ZHANG Fa-ming. Asymptotic Stability of a Class of Time Delays Cellular Neural Networks [J]. Journal of Changsha Communications University, 2004,20(2):7-9.
[7]廖晓昕,肖冬梅.具有变时滞的Hopfield型神经网络的全局指数稳定性[J].电子学报,2000;28(4):87-90.
LIAO Xiao-xin, XIAO Dong-mei. Globally Exponential Stability of Hopfield Neural Networks with Time-varying Delays[J]. Acta Electronica Sinica, 2000,28(4):87-90.
[8]周冬明,曹进德. 时滞细胞神经网络的稳定性分析[J]. 信息与控制, 1998,27(1): 32-37.
ZHOU Dong-ming, CAO Jin-de. Stability Analysis on Delayed Cellular Neural Networks[J]. Information and Control, 1998,27(1): 32-37.
[9]宋乾坤. 具有时滞细胞神经网络模型的全局指数稳定性[J]. 生物数学学报, 2003,18(4): 433-438.
SONG Qian-kun. Global Exponential Stability of Cellular Neural Networks with Time Delays[J]. Journal of Biomathematics, 2003,18(4): 433-438.
[10]彭世国. 变时延细胞神经网络模型的全局指数稳定性[J]. 工程数学学报, 2002,19(2): 131-134.
PENG Shi-guo. Globally Exponential Stability of Cellular Neural Networks with Time-varying Delays[J]. Journal of Engineering Mathematics, 2002, 22(4): 391-396.
[11]CENG Zhi-gang, FU Chao-jin, LIAO Xiao-xin. Stability Analysis of Neural Networks with Infinite Time-varying Delay[J]. Journal of Mathematics, 2002,24(2):93-95.
[12]侯学刚. 时滞细胞神经网络模型的全局吸引性和全局指数稳定性[J]. 四川师范大学学报(自然科学版), 2002,25(4):358-361.
HOU Xue-gang. Global Attractivity and Global Exponential Stability for Delayed Cellular Neural Networks Models[J]. Journal of Sichuan Normal University(Natural Science), 2002,25(4):358-361.
[13]HALANOY A. Differential Equations: Stability Oscillations Time-lags[M]. New York: Academic Press, 1966.
[14]BEMAN A, PLEMMONS R J. Nonnegative Matrices in the Mathematical Science[M]. New York: Academic Press, 1979.
收稿日期:2004-08-20
基金项目:湖南省自然科学基金资助项目(01JJY3029)
作者简介:张发明(1964-),男,湖南醴陵人,副教授,从事微分方程及现代控制理论的研究
论文联系人: 张发明,男,副教授;电话:0733-2622032(O); E-mail: zhang253@hotmail.com
摘要: 利用Brouwer不动点定理,证明了具有变时滞的细胞神经网络模型平衡点的存在性;利用Barbarlet引理、Dini导数与导数之间的关系,构造了一个特殊的Lyapunov函数,表明具有变时滞的细胞神经网络模型存在惟一全局指数平衡点并且全局渐近稳定;在此基础上,通过构造一个新的M-矩阵,利用Halanay时滞微分不等式和M-矩阵的特性,得出:细胞神经网络模型在一定的条件下,在平衡点处,全局指数稳定且与时滞无关。
关键词: Lyapunov函数; 细胞神经网络; 渐近稳定性; 指数稳定性
中图分类号:O231.5 文献标识码:A 文章编号: 1672-7207(2005)01-0128-05
