基于热-结构耦合的高炉无钟炉顶阀箱疲劳寿命预测
赵利华1,张开林1,张 键2
(1. 西南交通大学 牵引动力国家重点实验室,四川 成都,610031;
2. 北京首钢设计院,北京,100043)
摘 要:
摘 要:根据装料设备的工作流程,确定阀箱3种最不利的载荷工况;基于热-结构耦合理论并利用有限元分析软件ANSYS研究阀箱在温度载荷和机械载荷作用下的热-结构耦合问题,得到实际工况下阀箱的温度场、应力场以及危险部位的应力谱;依据裂纹萌生和扩展理论对阀箱进行疲劳寿命预测。研究结果表明,在3种载荷工况作用下阀箱应力均低于材料的屈服强度,其安全系数为1.8~3.2,且阀箱的变形在允许范围之内,阀箱静强度及刚度满足要求;阀箱疲劳寿命大于107,也满足要求。
关键词:
中图分类号:TF321.3 文献标识码:A 文章编号:1672-7207(2009)05-1312-06
Fatigue life prediction of clack box of bell-less top of large
blast furnace based on thermal-structural coupling
ZHAO Li-hua1, ZHANG Kai-lin1, ZHANG Jian2
(1. Traction Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031, China;
2. Beijing Shougang Design Institute, Beijing 100043, China)
Abstract: Based on the work flow of charging equipment, three worst work conditions of the clack box were defined. Then, based on thermal-structure coupled theory, the thermal-structure coupled of the clack box which suffered from mechanical and temperature load was analyzed using the powerful software ANSYS. The clack box’s temperature field and stress field as well as the stress spectrum of danger area in actual working condition were obtained. Finally, based on crack initiation and crack extension theory, the clack box’s fatigue life was predicted. The results show that the stress of clack box is lower than the yield limit of the material. The safety factor is between 1.8 and 3.2, and the distortion of clack box is in the permission scope. The static strength and stiffness satisfy the request, and the life of clack box exceeds 107, which meets the requirements.
Key words: thermal-structural coupled analysis; temperature field; stress field; crack; fatigue life; prediction
炉顶设备无钟化是现代大型高炉的发展方向。无钟炉顶较之有钟炉顶具有密度低、高度小、布料灵活、维修简便等优点[1-4]。阀箱是无料钟炉顶设备的主要部件之一,阀箱除承受炉顶设备和炉料的重力作用外,还承受高炉煤气的高温高压作用。为了在正式投入使用前,使设计者准确地预知阀箱的危险区域,本文作者采取相应的防范措施和优化,对阀箱进行热-结构耦合有限元分析;此外,依据危险部位的应力谱,并利用裂纹萌生和扩展理论对阀箱疲劳寿命进行预测。
1 热-结构耦合分析
耦合分析可分为顺序耦合和直接耦合2类。顺序耦合就是将前一种分析的结果作为已知边界条件,进行另外一种物理场分析的分析方法;直接耦合使将所有的边界条件同时施加在待分析的结构或系统上,从而使对各种不同物理场的分析同时进行。采用顺序耦合对阀箱进行分析的步骤是:基于能量守恒原理的热平衡方程,用有限元法计算出各节点的温度,并导出其他热物理参数;在进行应力分析时将温度场作为体载荷加到模型上,得到热-结构耦合分析结果。
1.1 温度场模型的建立
稳态热分析可以通过有限元计算确定由于稳定的热载荷引起的温度、热梯度、热流率、热流密度等参数。如果系统的净热流率为0,即流入系统的热量加上系统自身产生的热量等于流出系统的热量:![]() +
+![]() -
-![]() =0,则系统处于热稳态。在稳态热分析中,任一节点的温度不随时间变化,即稳态温度场的场函数仅仅是空间域函数[1]。在稳定的工作状态下,阀箱的温度波动很小,因此,可以认为阀箱的温度场是一个无内热源的稳态温度场,并假定阀箱材料为常物性材料,则其温度场分布函数T(x, y, z, t)在直角坐标系中满足热传导微分方程:
=0,则系统处于热稳态。在稳态热分析中,任一节点的温度不随时间变化,即稳态温度场的场函数仅仅是空间域函数[1]。在稳定的工作状态下,阀箱的温度波动很小,因此,可以认为阀箱的温度场是一个无内热源的稳态温度场,并假定阀箱材料为常物性材料,则其温度场分布函数T(x, y, z, t)在直角坐标系中满足热传导微分方程:

和高温煤气相接触的阀箱内壁为第一类边界条件,温度为固定值,不随时间和空间位置而改变。在稳定工作状态下,煤气温度为150 ℃。暴露于空气中的阀箱外壁为第三类边界条件,即对流换热边界条件。根据傅里叶定律和牛顿冷却公式,第三类边界条件的数学表达式为:

利用有限元原理,用Galerkin法构造近似函数,将近似函数带入温度场微分方程(1)和边界条件方程(2)中,因近似函数不满足方程(1)会产生余量,通过选择权函数,使得余量的加权积分为0[2-3]。组成n(有限元结点个数)个联立的线性代数方程组,写成矩阵形式 如下:
DTT=Q。 (3)
式中:DT为传导矩阵,包含导热系数、对流系数;T为结点温度向量;Q为结点热流率向量。通过求解方程(3)就可以得到结点温度。
1.2 热与结构耦合应力场分析
当物体各部分温度发生变化时,由于自由膨胀受到某种约束而产生热应力。当物体受外力和温度共同作用时,根据线性热应力理论,应力由两部分叠加,其中一部分是与温度变化成比例在所有方向上为相同的压力-βT(β为热应力系数),另一部分则认为是温度不变而由外力产生的应力[4-5]。在进行结构应力分析时将温度场作为体载荷加到有限元模型上,得到的结果即为热-结构耦合分析结果。根据文献[6],阀箱最大热-结构耦合Von Mises应力小于材料的屈服极限,阀箱整个区域在弹性范围之内,遵循热弹性理论,其结果满足如下方程。
物理方程:

热-结构耦合计算的有限元方程为:

2 有限元模型的建立
基于热-结构耦合理论,可以对阀箱的热与结构耦合应力场进行有限元分析。为了简化有限元计算过程,将阀箱上的螺栓孔、T型螺栓槽和热电偶接口等局部小开孔或开口忽略,这样简化的结果可能对那些存在开口的局部有影响,但对阀箱主体结构的计算结果影响不大。
有限元分析结果的精确度和网格划分是紧密相关的。对三维实体结构单元SOLID95和热分析单元SOLID90进行分析,这2种单元均为二次单元,而且在热分析与结构分析中可以满足顺序耦合的要求进行相互转换[7]。阀箱有限元模型共有58 905个节点,185 985个单元,如图1所示。阀箱所用材料为16MnR,该材料的屈服极限为345 MPa,强度极限为520 MPa。计算参数如表1所示。
表1 阀箱计算参数
Table 1 Parameter of clack box for calculation


图1 阀箱有限元模型
Fig.1 Finite element model of clack box
根据高炉无钟炉顶装料设备的工作流程,确定阀箱3种最不利的机械载荷工况,结果如表2所示。
表2 阀箱机械载荷工况
Table 2 Mechanical load cases of the clack box

根据机械载荷工况所确定的阀箱内壁受热区域、工程热分析所确定的阀箱外壁综合换热系数,计算出相应的阀箱温度场,进而得到阀箱热应力。机械载荷工况与相应的热应力构成耦合载荷工况,标记为耦合载荷工况Ⅰ,Ⅱ和Ⅲ。环境温度为20 ℃,阀箱外壁综合对流系数如表3所示。
表3 阀箱外表面综合换热系数
Table 3 Integrated heat transfer coefficient of surface of clack box

3 计算结果与分析
3.1 阀箱温度场计算结果
采用上述有限元分析模型,根据机械载荷工况所确定的阀箱内壁受热区域、工程热分析所确定的阀箱外壁综合换热系数,计算相应的阀箱温度场。图2所示为工况载荷Ⅲ作用时相应的阀箱温度场。

图2 工况载荷Ⅲ作用时相应的阀箱温度场
Fig.2 Temperature field of clack box under load of case Ⅲ
3.2 热-结构耦合应力场的计算结果及分析
利用顺序耦合方式进行热-耦合应力场计算,计算结果如图3和图4所示。阀箱在工况载荷Ⅰ,Ⅱ和Ⅲ作用下,危险部位A,B,C和D处的最大von Mises

图3 工况载荷Ⅰ作用下Von Mises应力云图
Fig.3 Von Mises stress field under load of case Ⅰ

图4 工况载荷Ⅲ作用下Von Mises应力云图
Fig.4 Von Mises stress field under load of case Ⅲ
等效应力σA,σB,σC和σD及左右3个压头的相对垂向位移如表4所示。
表4 各工况下危险部位处最大Von Mises等效应力及压头的相对位移
Table 4 Maximal Von Mises equivalent stress of dangerous parts and relative displacement of pressure head under different coupling load

阀箱在工况载荷Ⅰ~Ⅲ作用下,发生弯曲变形,虽然最大应力点的位置随载荷工况的不同而变化,但危险点总是集中在A,B,C和D这4个部位上,其各部位最大Von Mises应力均小于材料的屈服极限345 MPa,安全系数为1.8~3.2,达到常规设计所要求的安全系数(1.5~2.0)[8],阀箱静强度满足使用要求。
在工况载荷Ⅰ和Ⅱ作用下,阀箱受力严重不对称,阀箱在弯曲的同时又附带有翘曲,致使满料罐侧3个压头的相对垂向位移较大,而空料罐侧3个压头的相对垂向位移较小。在工况载荷Ⅲ作用下,阀箱受力近似对称,阀箱只产生微小的弯曲变形,致使左右3个压头的相对垂向位移较小。在工况载荷Ⅰ~Ⅲ作用下,左右3个压头的相对垂向位移均小于所规定的极限位移1 mm,阀箱刚度满足要求。
3.3 疲劳寿命估算
按照疲劳过程两阶段论,将疲劳寿命分为裂纹萌生寿命和裂纹扩展寿命,二者之和称为疲劳破坏总 寿命。
3.3.1 阀箱裂纹萌生寿命的计算
ANSYS的分析结果考虑了疲劳缺口系数,即ANSYS的分析结果是局部应力、应变分析结果。裂纹萌生寿命计算公式为[9-10]:

3.3.2 阀箱裂纹扩展寿命计算
把裂纹的扩展阶段可分为疲劳小裂纹的扩展阶段和宏观裂纹的扩展阶段,过渡裂纹尺寸l0由门槛应力强度因子范围?Kth和试样的疲劳极限σe求出;临界裂纹尺寸lc由临界值Kc求出。假设在裂纹形成阶段形成的起始裂纹长度l为0.1 mm。裂纹尺寸l在[0.1,l0]范围内时为小裂纹,在[l0,lc]时为宏观裂纹[11-12]。
由参考文献查得的?Kth是在一定的应力比下的结果,?Kth随应力比的增大而下降,依文献[13]推荐的公式换算:

3.3.3 疲劳寿命的估算结果
总寿命为:
![]()
裂纹形成与扩展阶段寿命估算结果如表5和表6所示。在B部位应力幅值较大,循环寿命偏低,但仍然大于107,阀箱寿命满足要求。
表5 裂纹形成与扩展阶段寿命估算数据
Table 5 Data of calculating periods of engendering crack and crack developing
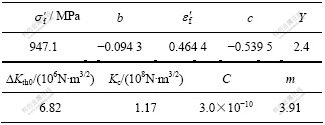
表6 阀箱危险部位疲劳寿命估算结果
Table 6 Estimate results of fatigue life of clack box’s dangerous parts

4 结 论
a. 通过热-结构耦合分析,阀箱在工况载荷Ⅰ~Ⅲ作用下,其各部位最大Von Mises应力均小于材料的屈服极限345 MPa,安全系数为1.8~3.2,达到常规设计所要求的安全系数,阀箱静强度满足使用要求。
b. 在工况载荷Ⅰ~Ⅲ作用下,左右3个压头的相对垂向位移均小于所规定的极限位移1 mm,阀箱刚度满足要求。
c. 通过对工况载荷Ⅰ~Ⅲ进行热-结构耦合计算,得到危险部位的应力谱,依据裂纹萌生和扩展理论对阀箱疲劳寿命进行预测,其疲劳寿命大于107,阀箱寿命满足要求。
参考文献:
[1] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 1998: 141-146.
YANG Shi-ming, TAO Wen-quan. Heat transfer theory[M]. Beijing: Higher Education Press, 1998: 141-146.
[2] 石 琳, 程素森, 张利君. 高炉铜冷却壁的热变形[J]. 中国有色金属学报, 2005, 15(12): 2040-2046.
SHI Lin, CHENG Su-sen, ZHANG Li-jun. Thermal distortion of blast furnace copper staves[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(12): 2040-2046.
[3] Rohsenow W M. Handbook of heat transfer fundamentals[M]. New York: New York McGraw-Hill Book Co, 1985.
[4] 罗子健, 杨 旗, 姬婉华. 考虑变形热效应的本构关系建立方法[J]. 中国有色金属学报, 2000, 10(6): 804-808.
LUO Zi-jian, YANG Qi, JI Wan-hua. New method to establish constitutive relationship considering effect of deformation heating[J]. The Chinese Journal of Nonferrous Metals, 2000, 10(6): 804-808.
[5] Hetnarski R B. Thermal stresses[M]. New York: North-Holland, 1986: 93-126.
[6] 赵利华, 张开林, 张红军. 高炉用无料钟炉顶阀箱力学性能分析报告[R]. 成都: 西南交通大学牵引力国家重点实验室, 2005.
ZHAO Li-hua, ZHANG Kai-lin, Zhang Hong-jun. Mechanical properties analysis report for clack box of bell-less top of large blast furnace[R]. Chengdu: Traction Power State Key Laboratory, Southwest Jiaotong University, 2005.
[7] 张朝晖. ANSYS8.0热分析教程与实例解析[M]. 北京: 中国铁道出版社, 2005: 205-238.
ZHANG Chao-hui. ANSYS8.0 thermal analysis course and example analysis [M]. Beijing: China Railway Press, 2005: 205-238.
[8] 董大勤, 袁凤隐. 压力容器设计手册[M]. 北京: 化学工业出版社, 2006: 132-143.
DONG Da-qin, Yuan Feng-yin. Handbook of pressure vessel design[M]. Beijing: Chemical Industry Press, 2006: 132-143.
[9] 徐 灏. 机械设计手册: 第二卷[M]. 北京: 机械工业出版社, 1991: 668-686.
XU Hao. Handbook of machine design: Volume Ⅱ[M]. Beijing: Machinery Industry Press, 1991: 668-686.
[10] 徐 慧, 伍晓赞, 程仕平, 等. 复合裂纹的应力强度因子有限元分析[J]. 中南大学学报: 自然科学版, 2007, 38(1): 79-83.
XU Hui, WU Xiao-zan, CHENG Shi-ping, et al. Finite element analysis of stress intensity factor in composite mode crack[J]. Journal of Central South University: Science and Technology, 2007, 38(1): 79-83.
[11] 赵少汴, 王忠保. 抗疲劳设计—方法与数据[M]. 北京: 机械工业出版社, 1997: 89-99.
ZHAO Shao-bian, WANG Zhong-bao. Anti-fatigue design-methods and data[M]. Beijing: Machinery Industry Press, 1997: 89-99.
[12] 王业双, 丁文江, 王渠东. 微机系统在合金热裂行为测试中的应用[J]. 中国有色金属学报, 2001, 11(1): 52-55.
WANG Ye-shuang, DING Wen-jiang, WANG QU-dong. Microcomputer system for hot-cracking testing of alloy[J]. The Chinese Journal of Nonferrous Metals, 2001, 11(1): 52-55.
[13] Suresh S. 材料的疲劳[M]. 王中光, 译. 北京: 国防工业出版社, 1999: 172-398.
Suresh S. Material fatigue[M]. WANG Zhong-guang, Trans. Beijing: Defense Industry Press, 1999: 172-398.
[14] Jaap S. Fatigue of structures and materials[M]. Dordrecht: Kluwer Academic, 2001: 137-154.
[15] 张 斌, 郭万林. 考虑闭合效应和三维应力约束的表面裂纹扩展模拟[J]. 计算力学学报, 2005, 22(6): 716-721.
ZHANG Bin, GUO Wan-lin. Numerical simulation of surface crack propagation considering the crack closure effects and the three-dimensional stress constraints[J]. Chinese Journal of Computational Mechanics, 2005, 22(6): 716-721.
收稿日期:2008-11-14;修回日期:2009-03-15
基金项目:长江学者和创新团队发展计划项目(IRT0452)
通信作者:赵利华(1977-),男,河北藁城人,博士研究生,从事结构的疲劳与可靠性研究;电话:13982275163;E-mail: zhaolihua1323@163.com
[1] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 1998: 141-146.
[5] Hetnarski R B. Thermal stresses[M]. New York: North-Holland, 1986: 93-126.
[6] 赵利华, 张开林, 张红军. 高炉用无料钟炉顶阀箱力学性能分析报告[R]. 成都: 西南交通大学牵引力国家重点实验室, 2005.
[7] 张朝晖. ANSYS8.0热分析教程与实例解析[M]. 北京: 中国铁道出版社, 2005: 205-238.
[8] 董大勤, 袁凤隐. 压力容器设计手册[M]. 北京: 化学工业出版社, 2006: 132-143.
[9] 徐 灏. 机械设计手册: 第二卷[M]. 北京: 机械工业出版社, 1991: 668-686.
[10] 徐 慧, 伍晓赞, 程仕平, 等. 复合裂纹的应力强度因子有限元分析[J]. 中南大学学报: 自然科学版, 2007, 38(1): 79-83.
[11] 赵少汴, 王忠保. 抗疲劳设计—方法与数据[M]. 北京: 机械工业出版社, 1997: 89-99.
[12] 王业双, 丁文江, 王渠东. 微机系统在合金热裂行为测试中的应用[J]. 中国有色金属学报, 2001, 11(1): 52-55.
[13] Suresh S. 材料的疲劳[M]. 王中光, 译. 北京: 国防工业出版社, 1999: 172-398.
[14] Jaap S. Fatigue of structures and materials[M]. Dordrecht: Kluwer Academic, 2001: 137-154.
" target="blank">[15] 张 斌, 郭万林. 考虑闭合效应和三维应力约束的表面裂纹扩展模拟[J]. 计算力学学报, 2005, 22(6): 716-721.ZHANG Bin, GUO Wan-lin. Numerical simulation of surface crack propagation considering the crack closure effects and the three-dimensional stress constraints[J]. Chinese Journal of Computational Mechanics, 2005, 22(6): 716-721.


