
Effects of material properties on power spinning process of
parts with transverse inner rib
MA Fei(马 飞)1, 2, YANG He(杨 合) 1, ZHAN Mei(詹 梅) 1
1. State Key Laboratory of Solidification Processing, School of Materials Science and Engineering,
Northwestern Polytechnical University, Xi’an 710072, China;
2. Changzheng Machinery Factory, Chengdu 610100, China
Received 11 March 2009; accepted 10 July 2009
Abstract:
Material properties of blank have a great effect on power spinning process of aluminum alloy parts with transverse inner rib. By using finite element(FE) and Taguchi method, the effects and significance of five key material parameters, namely, anisotropic index in thickness direction, yield strength, hardening exponent, strengthening factor and elastic modulus on the formability of inner rib, tendency of wall fracture and degree of inhomogeneous deformation of finished spun parts were obtained. The achievements provide an important guide for selecting reasonable spinning material, and are very significant for the optimum design and precision control of power spinning process of parts with transverse inner rib.
Key words:
power spinning; inner rib; Taguchi method; FEM; material properties;
1 Introduction
Spinning is an advanced continuous and local metal forming process, which is widely used in many fields due to its advantages of flexibility, light weight, high quality and low cost[1-4]. In the latest years, to satisfy the increasing demand of aerospace, astronautics, military industries and so on, power spinning is used to manufacture the high-strength and high-precision parts with transverse inner rib[5-6]. The conical parts with transverse inner rib and the schematic diagram of its power spinning process are shown in Figs.1 and 2, respectively.
In power spinning process of parts with transverse inner rib, material properties of blank have a great effect on stress-strain state and metal flow in plastic deformation zone. Recently, more and more scholars have placed emphasis on the effect of material properties on spinning process[7-8]. However, literature about the significance of material properties on spinning process has been scant. So, it is difficult for the previous work to provide theoretical guide for selecting reasonable spinning material in practical production. Compared with

Fig.1 Conical parts with transverse inner rib
traditional spinning process, the forming mechanism in power spinning process of conical parts with transverse inner is more complex. Until now, literature about the effects and significance of material properties on this process has less been reported. Hence, it is valuable to thoroughly and systematically study the effects and significance of material properties of blank in this process.
In this study, five key material parameters including anisotropic index in thickness direction r, yield strength σ0, hardening exponent n, strengthening factor K and elastic modulus E were matched regularly according to Taguchi’s orthogonal array, which led to various materials of aluminum alloy. Then, based on the FE method, the processes using different materials of aluminum alloy were simulated; the effects and significance of material parameters of blank on the formability of inner rib, tendency of wall fracture and degree of inhomogeneous deformation in finished spun parts were obtained by using Taguchi’s tools such as S/N ratio, factor effect analysis and analysis of variance (ANOVA).

Fig.2 Schematic diagram of power spinning process of conical parts with transverse inner rib
2 Taguchi method and 3D-FE model
2.1 Taguchi method
Taguchi method provides a simple, efficient and systematic approach to study the entire parameter space only with a few experiments and finally to obtain the optimization of forming conditions[9]. Recently, Taguchi method has been successfully applied to many manufacturing fields[10-13]. The main steps in the application of Taguchi method are as follows.
2.1.1 Determination of research objective
The research objective of this study is determined to obtain the effects and significance of material parameters on power spinning process of conical parts with transverse inner rib and to provide a basic rule for selecting reasonable spinning material in this process.
2.1.2 Selection of quality index
In power spinning process of conical parts with transverse inner rib, the common forming defects are undesired inner rib, wall fracture and inner crack. In order to quantitatively evaluate the effects of material properties on this process, after making an investigation on the forming mechanism of this process, the hoop tensile strain, radial tensile strain and degree of inhomogeneous deformation have been selected as quality indexes in this study. Radial direction is defined as the direction parallel to the generatrix of mandrel. In general, the smaller the hoop tensile strain, the radial tensile strain and the degree of inhomogeneous deformation, the smaller the possibility that undesired inner rib occurs, wall fracture and inner crack occur in the forming process. So, the-lower-the-better type S/N ratio was adopted in this study.
2.1.3 Selection of factors and their levels
In this study, five key material parameters including anisotropic index in thickness direction r, yield strength σ0, hardening exponent n, strengthening factor K and elastic modulus E were selected as influencing factors. Four levels, having equal spacing within the range of aluminum alloy, were selected for each influencing factor [14-15]. Detailed information is listed in Table 1.
Table 1 Standard L16 (45) OA with factors and levels

2.1.4 Selection of orthogonal array(OA)
In the application of Taguchi method, it is a key step to select appropriate OA. In this study, the L16 (45) OA was selected and its layout with factors and levels assignments is listed in Table 1. According to the match of material parameters in Table 1 and the format of constitutive equation ![]() , it is found that sixteen different materials of aluminum alloy can be determined in this study.
, it is found that sixteen different materials of aluminum alloy can be determined in this study.
2.1.5 Data processing
1) Calculation of S/N ratio
In this study, the-lower-the-better type S/N ratio, as given below was applied for processing the raw data:
![]() (1)
(1)
where η is the S/N ratio for the-lower-the-better case, Yi is the measured quality index for the ith repetition, and N is the number of repetitions in a trial.
2) Level average response analysis
Level average response analysis helps in analyzing the trend of quality index with respect to the variation of factors and optimizing the quality index. In this study, the level average response analysis based on S/N ratio was selected.
3) Analysis of variance (ANOVA)
In order to determine the significance of factors influencing the quality index, analysis of variance based on S/N ratio was performed in this study. The total sum of square ST from the S/N ratio is
![]() (2)
(2)
where N is the number of the experiments, e.g. N=16, Yi is the S/N ratio of quality index. The sum of square SP of the factor P can be calculated as
![]() (3)
(3)
where j is the level number of factor P, t is the repetition of each level of the factor P. ![]() is the sum of the S/N ratio of factor P at level i. The sum of square from error parameters is
is the sum of the S/N ratio of factor P at level i. The sum of square from error parameters is
Se=ST-SA-SB-SC-SD-SE (4)
The total degree of freedom is
DT=N-1 (5)
The degree of freedom for factor P is
DP=t-1 (6)
The variance of factor P is
VP=SP/DP (7)
Then, the F value for factor P, namely, the ratio of the mean of square deviations to the mean of square error is
FP=VP/VE (8)
The percentage contribution ρP can be calculated as
ρP=SP/ST (9)
2.2 3D-FE model and determination of calculation conditions
Fig.3 shows the 3D-FE model of power spinning process of aluminum alloy conical parts with transverse inner rib, which is developed based on the ABAQUS/ Explicit environment. In this 3D-FE model, the mandrel is discretized as disperse rigid body, the roller is looked as analytic rigid body, and the blank is meshed with 8-noded first-order reduction integration continuum elements (C3D8R). The mesh size is determined by performing a mesh convergence study. The adaptive remeshing and hourglass control technologies were also employed to reduce distortion of elements and to control the mode of zero energy. The main forming parameters are listed in Table 2. This 3D-FE model has been verified in experiment[5]. Thus, based on this validated 3D-FE model, the numerical simulation results in this study can be considered to be valid.

Fig.3 3D-FE model of power spinning process of aluminum alloy conical parts with transverse inner rib
Table 2 Main forming parameters

3 Results and discussion
According to the Taguchi method, the research scheme was determined and the data processing of simulation results were performed. The ANOVA results for hoop tensile strain, radial tensile strain and degree of inhomogeneous deformation are shown in Tables 3, 4 and 5, respectively. The level average response plots for hoop tensile strain, radial tensile strain and degree of inhomogeneous deformation based on raw data are shown in Figs.4, 5 and 6, respectively. Based on the above work, the effects and significance of the five key material parameters on the formability of inner rib, tendency of wall fracture and degree of inhomogeneous deformation of finished spun part have been obtained.
3.1 Formability of inner rib
In power spinning process of conical parts with transverse inner rib, the larger the hoop tensile strain, the larger the clearance between mandrel and spun parts. Obviously, the larger clearance between mandrel and spun parts is harmful to the formation of inner rib. So, the hoop tensile strain can be selected as an index to evaluate the forming quality of inner rib, namely, the formability of inner rib: the smaller the hoop tensile strain becomes, the better the formability of inner rib is. Table 3 and Fig.4 show the ANOVA results and level average response of hoop tensile strain, respectively.
Table 3 shows that hardening exponent n is the
prominent factor influencing the hoop tensile strain, anisotropic index in thickness direction r is the next prominent factor influencing the hoop tensile strain; the elastic modulus E, yield strength σ0 and strengthening factor K have a neglected effect on the hoop tensile strain. Fig.4 indicates that the larger the hardening exponent n or the smaller the anisotropic index in thickness direction r, the smaller the hoop tensile strain, namely, the better the formability of inner rib. The reason is that the larger the hardening exponent n is, the larger the capability of plastic deformation, which is obviously helpful to the formability of inner rib; the larger the anisotropic index in thickness direction r is, the smaller the metal flow in thickness direction is, and then the metal flow increases in both circumference and radial direction, which is harmful to the formability of inner rib in this process. In the optimum design of the formability of inner rib in finished spun parts, these conclusions can provide an important guide for selecting reasonable spinning material in power spinning process of conical parts with transverse inner rib.
Table 3 ANOVA results of hoop tensile strain

Table 4 ANOVA results of radial tensile strain

Table 5 ANOVA results of degree of inhomogeneous deformation

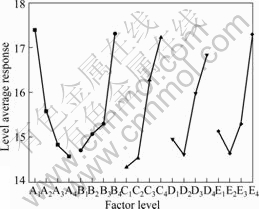
Fig.4 Level average response for hoop tensile strain based on S/N ratio

Fig.5 Level average response for radial tensile strain based on S/N ratio

Fig.6 Level average response for degree of inhomogeneous deformation based on S/N ratio
3.2 Tendency of wall fracture
In power spinning process of conical parts with transverse inner rib, radial tensile strain can be selected as the index to evaluate the tendency of wall fracture. The smaller the radial tensile strain, the smaller the tendency of wall fracture in finished spun parts. Table 4 and Fig.5 show the level average response and ANOVA results of radial tensile strain.
Table 4 indicates that the hardening exponent n and anisotropic index in thickness direction r are the prominent factors influencing radial tensile strain, and the strengthening factor K, elastic modulus E and yield strength σ0 have a neglected effect on the radial tensile strain. Fig.5 illustrates that the larger the hardening exponent n or the smaller the anisotropic index in thickness direction r, the smaller the radial tensile strain, namely, the smaller the tendency of wall fracture of deformed blank. The reason is that the larger the hardening exponent n, the more notable the strain-hardening and the more even the plastic deformation in this forming process, so the smaller the tendency of wall fracture of deformed blank; the larger the anisotropic index in thickness direction r, the more difficult the metal flow in thickness direction, so metal flow in circumference direction increases. In this process, metal flow in circumference direction results in diameter expanding of deformed blank, which results in larger radial tensile stress in the subsequent forming process. So, the tendency of wall fracture increases. In the optimum design of the tendency of wall fracture in finished parts, these conclusions can provide an important guide for selecting reasonable spinning material in power spinning process of conical parts with transverse inner rib.
3.3 Degree of inhomogeneous deformation
The degree of inhomogeneous deformation ψid is defined as the ratio of the difference between the maximum and minimum equivalent plastic strain to the maximum equivalent plastic strain. The expression is
![]() (10)
(10)
where ![]() and
and ![]() are the maximum and minimum equivalent plastic strains of finished spun parts, respectively. In power spinning process of conical parts with transverse inner rib, the finished spun parts will produce internal defects and surface crack due to drastic inhomogeneous deformation[16], which finally results in poor mechanical property. Table 5 and Fig.6 show the ANOVA results and level average response of the degree of inhomogeneous deformation, respectively.
are the maximum and minimum equivalent plastic strains of finished spun parts, respectively. In power spinning process of conical parts with transverse inner rib, the finished spun parts will produce internal defects and surface crack due to drastic inhomogeneous deformation[16], which finally results in poor mechanical property. Table 5 and Fig.6 show the ANOVA results and level average response of the degree of inhomogeneous deformation, respectively.
Table 5 illustrates that hardening exponent n is the prominent factor influencing the degree of inhomogeneous deformation, anisotropic index in thickness direction r and strengthening factor K are the next prominent factors influencing the degree of inhomogeneous deformation. Fig.6 shows that the larger the hardening exponent n, the anisotropic index in thickness direction r and the strengthening factor K, the smaller the degree of inhomogeneous deformation, namely, the better the mechanical property of finished spun parts. The reason is that the larger the hardening exponent n is, the more notable the strain hardening is and the more even the plastic deformation is. So, the degree of inhomogeneous deformation is smaller. The smaller the anisotropic index in thickness direction r is, the easier the deformation in thickness direction is and the more notable the metal accumulation ahead of the forming roller, which results in increasing thinning-ratio of deformed blank during this forming process. So, smaller anisotropic index in thickness direction r of blank results in drastic inhomogeneous deformation in this process. The elastic modulus E and yield strength σ0 have a neglected effect on the degree of inhomogeneous deformation. In the optimum design process of mechanical property in finished spun parts, these conclusions can provide an important guide for selecting reasonable spinning material in power spinning process of parts with transverse inner rib.
4 Conclusions
1) Hardening exponent n is the prominent factor influencing the formability of inner rib. Anisotropic index in thickness direction r is the next prominent factor influencing the formability of inner rib. The larger the hardening exponent n and the strengthening factor K, or the smaller the anisotropic index in thickness direction r, the better the formability of inner rib. The elastic modulus E, yield strength σ0 and strengthening factor K have a neglected effect on the formability of inner rib.
2) Hardening exponent n and anisotropic index in thickness direction r are the prominent factors influencing the tendency of wall fracture. The larger the hardening exponent n or the smaller the anisotropic index in thickness direction r, the smaller the tendency of wall fracture. The elastic modulus E, yield strength σ0 and strengthening factor K have a neglected effect on the tendency of wall fracture.
3) Hardening exponent n is the prominent factor influencing the degree of inhomogeneous deformation, anisotropic index in thickness direction r and strengthening factor K are the next prominent factors influencing the degree of inhomogeneous deformation. The larger the hardening exponent n, the anisotropic index in thickness direction r and the strengthening factor K, the smaller the degree of inhomogeneous deformation. The elastic modulus E and yield strength σ0 have a neglected effect on the degree of inhomogeneous deformation.
References
[1] WONG C C, DEAN T A, LIN J. A review of spinning, shear spinning and flow forming processes [J]. International Journal of Machine Tools and Manufacture, 2003, 43: 1419-1435
[2] EL-KHABEERY M M, FATTOUH M, EL-SHEIKH M N. On the conventional simple spinning of cylindrical aluminium cups [J]. International Journal of Machine Tools and Manufacture, 1991, 31(2): 203-219
[3] XIA Q X, CHENG X Q, HUA Y. Finite element simulation and experimental investigation on the forming forces of 3D non-axisymmetrical tubes spinning [J]. International Journal of Mechanical Sciences, 2006, 48: 726-735
[4] LEE H S, YOON J H, PARK J S. A study on failure characteristic of spherical pressure vessel [J]. Journal of Materials Processing Technology, 2005, 164/165: 882-888
[5] BAI Q, YANG H, ZHAN M. Finite element modeling of power spinning of thin-walled shell with hoop inner rib [J]. Trans Nonferrous Met Soc China, 2008, 18(1): 6-13
[6] MA Fei, YANG He, ZHAN Mei. Research on the blank selection in the power spinning process of parts with transverse inner rib [J]. Materials Science Forum, 2007, 561/562/563/564/565: 885-888
[7] ZHOU Qiang. Finite element simulation and experimental study on the power spinning process of cone parts with discontinuous wall thickness [D]. Xi’an: Northwestern Polytechnical University, 2007: 9-11
[8] MA Fei, YANG He, ZHAN Mei. Research on the effect of material parameters on the multi-pass conventional spinning process[C]// The Second International Symposium on Advanced Metal Forming Technology. Taiyuan: Chinese Plastic Engineering Society, 2005: 174-176
[9] HUANG Liang, YANG He, ZHAN Mei. Numerical simulation of influence of material parameters on splitting spinning of aluminum alloy[J]. Trans Nonferrous Met Soc China, 2008, 18: 674-681.
[10] TAGUCHI G. Introduction to quality engineering [M]. New York: Quality Resources, 1986: 1-30
[11] KWAN C T, JAN F S, LEE W C. An optimum die fillet design for minimizing the difference in extruded fin lengths of straight-fin heat sink extrusion [J]. Journal of Materials Processing Technology, 2008, 201: 145-149
[12] KANG J, HADFIELD M, Parameter optimization by Taguchi methods for finishing advanced ceramic balls using a novel eccentric lapping machine [J]. Proc Inst Mech Eng, 2001, 215B: 69-78
[13] KOMANDURI R, JIANG M. Application of Taguchi method for optimization of finishing conditions in magnetic floating polishing [J]. Wear, 1997, 213(1/2): 59-71
[14] SHAJI S, RADHAKRICHNAN V. Analysis of process parameters in surface grinding with graphite as lubricant based on the Taguchi method [J]. Journal of Materials Processing Technology, 2003, 141: 51-59.
[15] LI Heng. Study on wrinkling behaviors under multi-die constraints in thin-walled tube NC bending [D]. Xi’an: Northwestern Polytechnical University, 2007: 78-96 (in Chinese)
[16] GUO L G, YANG H, ZHAN M. Research on plastic deformation behaviour in cold ring rolling by FEM numerical simulation [J]. Modelling Simul Mater Sci Eng, 2005, 13: 1029-1046.
Foundation item: Projects(50405039, 50575186) supported by the National Natural Science Foundation of China; Project(50225518) supported by the National Natural Science Foundation of China for Distinguished Young Scholars; Project(2008AA04Z122) supported by the National High-tech Research and Development Program of China
Corresponding author: YANG He; Tel: +86-29-88495632; Fax: +86-29-88495632; E-mail: yanghe@nwpu.edu.cn
DOI: 10.1016/S1003-6326(09)60324-1


