中国有色金属学报(英文版)

Trans. Nonferrous Met. Soc. China 26(2016) 822-834

An elasto-plastic constitutive model for soft rock considering mobilization of strength

Hang-zhou LI¹, Guang-dong XIONG¹, Gui-ping ZHAO²

1. Department of Civil Engineering, Xi’an Jiaotong University, Xi’an 710049, China;

2. School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, China

Received 12 May 2015; accepted 10 November 2015

Abstract:

A new elasto-plastic constitutive model is presented in the framework of plasticity theory. The strength characteristics of a diatomaceous soft rock is investigated. The friction angle and cohesion of soft rock are mobilized as a function of plastic strain. A hyperbolic hardening function for the mobilized friction and a mixed parabolic and exponential equation for the mobilized cohesion are proposed. In view of the unified strength theory and the mobilizations of strength components, a yield function is given. A plastic potential function is determined by using the non-associated plastic flow rule. An elasto-plastic constitutive model is developed and verified. The results indicate that the proposed model can predict the behavior of soft rock accurately. The advantages of the proposed constitutive model are analyzed. The evidences support that the proposed constitutive model is a mixed hardening/softening model. A hump hardening/softening function for mobilized friction is extended to a more generalized condition.

Key words:

constitutive model; mobilized strength component; unified strength theory; soft rock;

1 Introduction

Soft rock is widely distributed in the world. The mechanical behavior of soft rock is complex and exhibits strain hardening or strain softening characteristics in a certain range of confining pressure. Although commonly used, it is difficult to describe the behavior of soft rock and even more complicated to develop constitutive models for its behavior. To guarantee stability in geotechnical engineering, it is essential to investigate the behavior of soft rock and develop a constitutive model that can capture main mechanical features. Some constitutive models for soft rock have been developed [1-5]. These models mentioned above well predict the behavior of some soft rocks in different ways and provide some highlights for the development of constitutive models.

As a cohesive-frictional material, the cohesion and friction in soft rock play an important role in resisting deformation and failure under loading. In classical strength theory, such as the Mohr-Coulomb criterion, the strength components of material are assumed to be mobilized simultaneously and keep constant. However, many evidences support some contradictory theoretical viewpoints about the traditional understanding. VERMEER and BORST [6], MARTIN [7], HAJIABDOLMAJID [8] and SCHMERTMANN and OSTERBERG [9] demonstrated that the strength components of soils and hard rocks are non-simultaneous mobilization, and the mobilizations of rocks and soils are clearly different. Furthermore, there are few evidences to support the mobilization of soft rocks.

VERMEER and BORST [6] found that it is a novel idea to introduce strength mobilization to develop a constitutive model. Some researchers [8,10-15] analyzed the strength characteristics of rocks and soils and developed various constitutive models by considering mobilization of strength components based on the idea of VERMEER and BORST [6]. But these models are based on the Mohr-Coulomb criterion and ignore the effect of the intermediate principal stress.

However, many studies demonstrated that the intermediate principal stress significantly affects the mechanical behavior of some rocks and soils [16-25]. ZHANG et al [2] studied the influence of intermediate principal stress on the mechanical behavior of soft rock based on plane strain tests.

Thus, it is necessary to develop a new constitutive model that can reflect the effect of the intermediate principal stress. A three-dimensional strength criterion must be introduced. Many strength criteria have been proposed, but no criterion can describe all geomaterials due to the complexity of the property of geomaterials. Thus, it is necessary to select a versatile criterion that can predict the behavior of geomaterials as possible. YU [26] surveyed the advances in strength theory (such as yield criteria and failure criteria) of several materials, including metallic materials, rock, soil, concrete, ice, iron, polymers, and energetic materials, under complex stresses, discussed the relationships between various criteria, and presented a method for choosing a reasonable failure criterion for research and engineering applications. LI et al [27] compared several strength criteria under a general stress state and found that the unified strength theory is most versatile. The unified strength theory has been widely recognized and used in geotechnical engineering and other areas of engineering and is summarized [28,29].

YU et al [30] developed a constitutive model based on the unified strength theory and applied it to analyze the stability of underground excavations. However, the constitutive model neglects the hardening law and is an ideal elasto-plastic model, which leads to several errors when predicting the behavior of geomaterials. LI et al [15] developed a constitutive model based on the unified strength theory by considering the mobilized friction and ignoring the effect of cohesion, but the model can only reflect strain softening behavior. The objective of this work is to investigate the mobilized strength components of soft rock based on experiments. In the framework of plasticity, a hardening/softening constitutive model is to be developed by considering the unified strength theory and the mobilization of strength.

2 Strength characteristics of soft rock

2.1 Experiment

To investigate the strength behavior of soft rock, a representative diatomaceous soft rock is considered in the present work. The diatomaceous soft rock was taken from the diatomaceous mud rock stratum at Noto Peninsula in Ishikawa Prefecture, Japan, and belongs to the late Miocene age (see Ref. [31]). The rock is composed of the debris of diatoms, clay and volcanic ash. The consolidation test of the rock indicates that the preconsolidation pressure of the rock is 1.5 MPa. A series of consolidated undrained triaxial compressive tests on saturated diatomaceous soft rock samples of 50 mm in diameter and 100 mm in length were performed. Herein, only the normally consolidated rock was investigated. Considering the need of practical engineering and the limitation of the maximum confining cell of triaxial apparatus, the confining pressures of 2, 2.5, 3 and 3.5 MPa, were adopted for the consolidated undrained test.

Figures 1 and 2 show the results of the stress-strain relationship and the pore water pressure-strain relationship under different confining pressures, respectively. The results in Fig. 1 indicate that the stress-strain behavior exhibits pronounced strain softening characteristics. The stress increases to a peak value with the increase of strain and then begins to decrease to residual value gradually. The peak strengths of the soft rock under different confining pressures occur in a range of the strain of 2.5%-4%. Figure 2 shows the relationship between pore pressure and strain. The pore pressure under different confining pressures increases with the increase of strain.

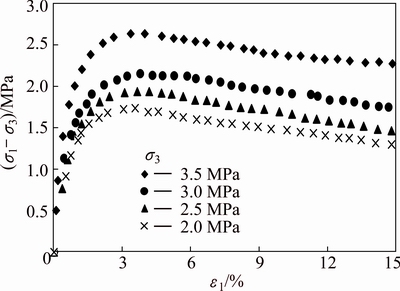
Fig. 1 Stress-strain curves of diatomaceous soft rock under different confining pressures

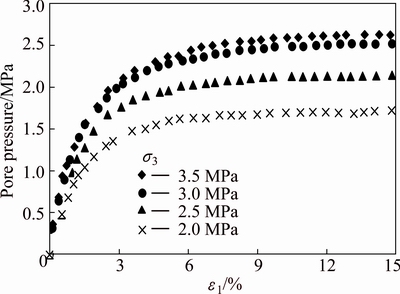
Fig. 2 Pore pressure-strain curves of diatomaceous soft rock under different confining pressures

2.2 Mobilization of strength

The strength of geomaterials is generally assumed to be composed of two parts, i.e., frictional strength component and cohesive strength component. Generally, the strength components are implicitly assumed to be mobilized instantly and act simultaneously when deformation occurs. For a work hardening material, the friction angle and the cohesion at failure are often adopted to analyze strength behavior or to evaluate the stability of engineering. For a work softening material, the peak or residual strength parameters are often chosen. In some situations, excessively large deformation is required to mobilize the peak or residual strength, which may cause instability of engineering. Thus, it is necessary to investigate the mobilization of strength of materials at a certain level. Many evidences have demonstrated that the strength components are not mobilized simultaneously. MARTIN [7,32] found that the frictional component of rock progressively hardens, while the cohesive components progressively weaken with damage to the rock. HANDIN [33] argued that the frictional component is not mobilized until the cohesion component is fully mobilized and sliding occurs. SCHMERTMANN and OSTERBERG [9] showed that the cohesion component of clay mobilizes at its maximum very early and drops sharply, while the friction component requires 10-20 times the strain to approach full mobilization. HAJIABDOLMAJID [8] summarized the strength mobilization of some types of rocks and soils and indicated that the strength components are non-simultaneous mobilization.

To investigate the mechanical behavior of a material more accurately, the key is to determine the strength parameters at any loading stage, which will be an aid to predict and guarantee the stability of engineering. When MARTIN [7] investigated the mobilization of strength of Lac du Bonnet granite in multiple loading and unloading tests, the cohesion and the friction angle in each load-unload cycle are defined as c=σ_cd/2, φ=2arctan(σ₁/σ_cd)-π/2, respectively, where σ_cd is the crack damage stress and equal to 80% of axial stress σ₁. 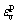The mobilization of cohesion and friction with respect to damage ω that is defined as the accumulated permanent volumetric strain (, where is the volumetric strain in a given load-unload cycle, and n is the cycle of loading-unloading) were then analyzed. The above method is based on axial cyclic loading test and is difficult to be utilized in other types of test, and the confinement also cannot be accounted for SULEM et al [10] and JAFARPOUR et al [12] calculated the mobilized friction angle and the cohesion of sandstone by keeping tension cut-off constant at peak strength in pre-peak regime in p-q coordinate, while in the softening regime, the frictional angle was assumed to remain constant and be equal to the value at the peak strength, which results in the decrease of tension cut-off and cohesion. Too many constraints are limited in the method, which results in some errors in investigating mechanical behavior of materials.

Herein, to study the mobilization of strength of soft rock, the stress state at any loading stage is assumed to reach a new limit equilibrium. In this case, a series of Mohr circles under different confining pressures can be drawn at any plastic strain and the corresponding Mohr failure envelope is obtained. The mobilized friction and cohesion are then determined from the envelope. An effective plastic strain parameter is used to represent the plastic strains and expressed as

                             (1)

where 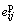 is the deviatoric strain tensor and defined as ,  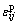is the strain tensor and δ_ij is Kronecker delta.

Figure 3 shows the change of the mobilization of frictional and cohesive components with plastic strain for the diatomaceous soft rock. The results indicate that they are not mobilized simultaneously and change as functions of plastic strain. The mobilized cohesion of the diatomaceous soft rock reaches the peak value very early, i.e., at very low plastic strain, and then drops to a residual value with strain, while the frictional component gradually increases to a maximum value that is equal to the residual friction angle of the soft rock. The strength mobilization of the soft rock is similar to that of clay demonstrated by SCHMERTMANN and OSTERBERG [9] as shown in Fig. 4. The difference is that the cohesion of soft rock reaches the maximum more early than that of clay.

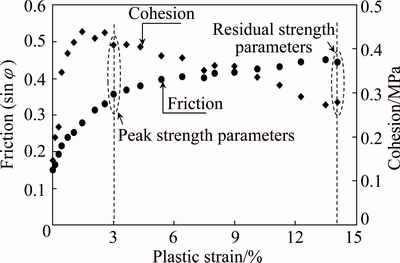
Fig. 3 Mobilization of friction and cohesion as function of plastic strain for diatomaceous soft rock

Cohesion is a type of inherent resistance between two adjacent particles. BISHOP [34] described that cohesion is contributed by two components: one is due to inter-particle bonds which have developed in nature on a geological time scale, which is largely destroyed by moderate shear strain or remolding; the other function of void ratio, present in remolded soil and probably related to the physic-chemical properties of bonded water, is likewise a function of strain and largely disappears on the slip surface formed at large post-peak displacements. From this perspective, the sharp increase of cohesive strength at low strain is due to the compactness of void in soft rock, while the drop is due to the fact that the increase of plastic strain causes internal particle bonds to continuously diminish and induces the micro-cracks growth and accumulation. Frictional strength mainly depends on inter-particle friction, dilatancy and interlocking structures, which increases with the increase of the applied stresses and requires considerable strain for its full mobilization. This is because the increase of stresses causes an increase of the inter-particle force at contact points between the particles and results in slip at contact points, which induces a rearrangement of particles, i.e., plastic deformation in a macroscopic sense.

Fig. 4 Mobilization of cohesion and friction as function of strain for Boston blue clay (after SCHMERTMANN and OSTERBERG [9])

3 Failure criterion

3.1 Unified strength theory

Many criteria have been developed to predict failure of materials, such as Mohr-Coulomb criterion, Hoek-Brown criterion, Lade criterion, Mogi criterion, Drucker-Prager criterion. Particularly, many evidences have indicated that the strength of materials is dependent on the intermediate principal stress as mentioned in introduction. To investigate the failure mechanism under a complex stress state, YU and HE [35] developed a unified strength theory that considers the contributions of all of the stress components that act on the stress element up to the yielding or failure of materials. The criterion assumes that the yielding of materials begins when the sum of the two larger principal shear stresses and the corresponding normal stress function reaches a magnitude C. The unified strength theory can be expressed as (YU and HE [35])

,

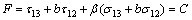when 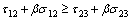                 (2a)

,

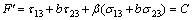when                 (2b)

where b is a parameter that reflects the influence of the intermediate principal shear stress τ₁₂ or τ₂₃ on the failure of material, which varies from 0 to 1, β is the coefficient that represents the effect of the normal stress on failure, C is the strength parameter of material. β and C can be determined by experimental results of uniaxial tension strength σ_t and uniaxial compression strength σ_c.

                        (3a)

                      (3b)

where τ₁₃, τ₁₂, and τ₂₃ are principal shear stresses and σ₁₃, σ₁₂ and σ₂₃ are the corresponding normal stresses acting on the sections where τ₁₃, τ₁₂, and τ₂₃ act, and they are defined as

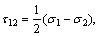
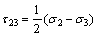    (4a)

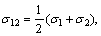
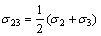    (4b)

Substituting Eqs. (3) and (4) into Eq. (2), the unified strength theory is expressed in terms of the principal stresses as

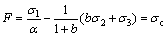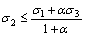 ()   (5a)

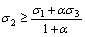()  (5b)

In geotechnical engineering, the strength is usually expressed in terms of the cohesion and the friction angle. Thus, the unified strength theory is also expressed as

,

when 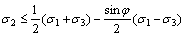         (6a)

,

when 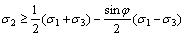         (6b)

where c and φ are the cohesion and friction angle of material, respectively.

The unified strength theory can reflect the fundamental characteristics of geomaterials, such as different tensile and compressive strengths, the hydrostatic pressure, the intermediate principal stress and its zonal change and material dependence [26]. It can form a series of criteria when b takes different values from 0 to 1, and its loci are shown in Fig. 5. The unified strength theory reduces to be the Mohr-Coulomb criterion that is the lower bound of the strength criteria when b=0, and to be a twin-shear strength theory (YU et al [36]) when b=1. It also becomes the Tresca criterion when b=0 and α=1 and the linear approximation of the von Mises criterion when b=1/2 and α=1.

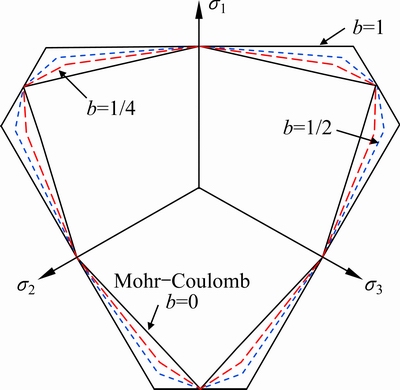
Fig. 5 Loci of unified strength theory in deviatoric plane

3.2 Verification of strength theory

Some polyaxial test data are used to verify the applicability of the unified strength theory for geomaterials. For rocks, the polyaxial test data from KTB amphibolites, Solenhofen limestone, and Dunham dolomite are collected [21,23]. The verified results are shown in Fig. 6. The unified strength theory can predict the strength of the KTB amphibolites, Solenhofen limestone and Dunham dolomite when b=0.5, 0.7, and 0.6, respectively. It reduces to be the Mohr-Coulomb criterion when b=0, which ignores the effect of the intermediate principle stress and its strength envelope is a horizontal line in σ₁－σ₂ space. For comparison, the unified strength with b=1.0 is also given, which overestimates the strength of these rocks. The results in Fig. 6 also further prove that the unified strength theory can represent many strength criteria when the value of b is different. For soils, YU et al [37] used the true triaxial test data of sand, clay and loess to verify the unified strength theory. The results indicated that the unified strength theory can accurately predict these soils. All of the evidences suggest that the unified strength theory is versatile.

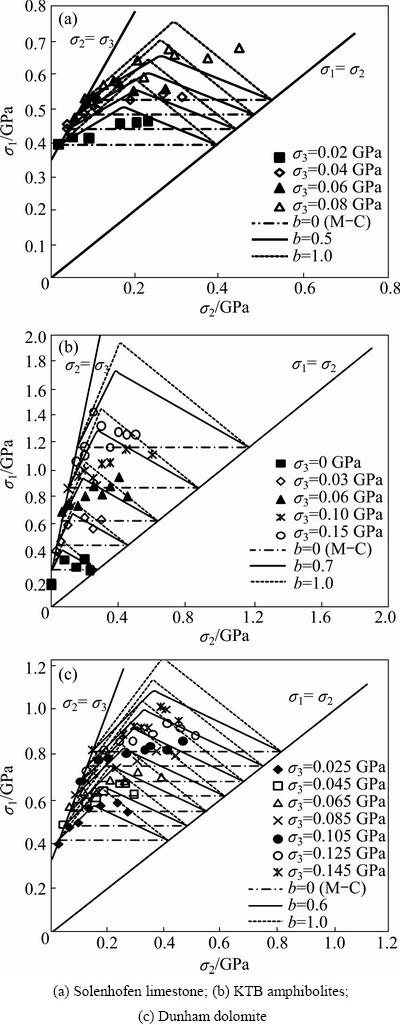
Fig. 6 Verification of unified strength theory for rocks (test data after [21, 23])

4 Constitutive model

4.1 Yield function

It can be concluded from the above demonstration in Section 2 that the cohesion and friction angle are not mobilized simultaneously. Thus, the conventional failure criteria cannot properly simulate the yield of materials, which can be illustrated by Fig. 7. Figure 7 indicates the strength envelope for the diatomaceous soft rock at different strain levels in (σ₁+σ₃)/2-(σ₁-σ₃)/2 coordinate. It further illustrates that the mobilization of strength components is not simultaneous and depends on the deformation and the stress level. If assuming the simultaneous mobilization of cohesive and frictional strength, the dash line represents a possible failure envelope, and any stress state in the shade zone in Fig. 7 can be reached. However, the situation is impossible to occur and violates the recognition of strength characteristics, this is because the cohesive strength is mobilized and degraded before the full mobilization of frictional component.

Fig. 7 Strength envelopes for diatomaceous soft rock at different strain levels

Soft rock belongs to a cohesive-frictional material and the strength components resisting the disintegration process under loading are due to cohesion and friction. Similar to the Mohr-Coulomb criterion, the unified strength theory is also composed of cohesive and frictional components. From this perspective, it is reasonable to adopt the criterion as a yield function in an elasto-plastic model to predict the behavior of soft rock. However, the unified strength theory in which the simultaneous mobilization of cohesion and friction is assumed has the shortcomings in predicting the failure of soft rock. If adopting the criterion as a yield function directly, an ideal elasto-plastic constitutive model is developed as YU et al [30]. Thus, a hardening parameter, e.g., defined by Eq. (1), must be introduced to account for the fact that the mechanical behavior of materials during yielding is not perfectly plastic but involves a decrease or increase in resistance. The cohesive and frictional mobilization have been illustrated as a function of plastic strain as shown in Fig. 3. Therefore, in view of the unified strength theory, a yield function expressed in terms of the principal stresses can immediately be defined as

when ,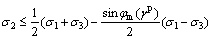

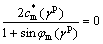                      (7a)

when ,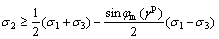

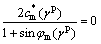                     (7b)

where γ^p is an effective plastic strain defined in Eq. (1), φ_m(γ^p) is the mobilized friction angle as a function of plastic strain, and (γ^p) ((γ^p)=c_m(γ^p)cos φ_m(γ^p) , for simplicity, is also called as the mobilized cohesion, which will be discussed in the following. Note that the yield function Eq. (7) differs from the expression of failure criterion Eq. (6), and the term sin φ is replaced by sin φ_m(γ^p), and ccos φ_m by (γ^p).

Alternatively to the above representations, it is also possible to describe the yield function in terms of stress invariants. In the invariant representation, the yield function is given as

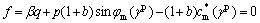    (8)

where

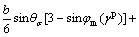
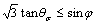    (9a)

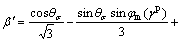
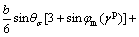
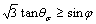    (9b)

where θ_σ is the Lode angle.

4.2 Hardening function

To predict the behavior of soft rock more accurately, a hardening function must be determined to reflect the change of a yield function when a material begins to yield. As mentioned above, the plastic strain dependent cohesive and frictional components are introduced into the yield function Eq. (7) and Eq. (8). The effective plastic strain defined in Eq. (1) is regarded as the hardening parameter in yield function and represents the accumulated plastic strain. Thus, the expression of the plastic strain dependent strength components, i.e., a hardening function, should be determined. Several forms of the mobilized strength component have been developed as listed in Table 1.

Table 1 Mobilization of cohesive and frictional strength components

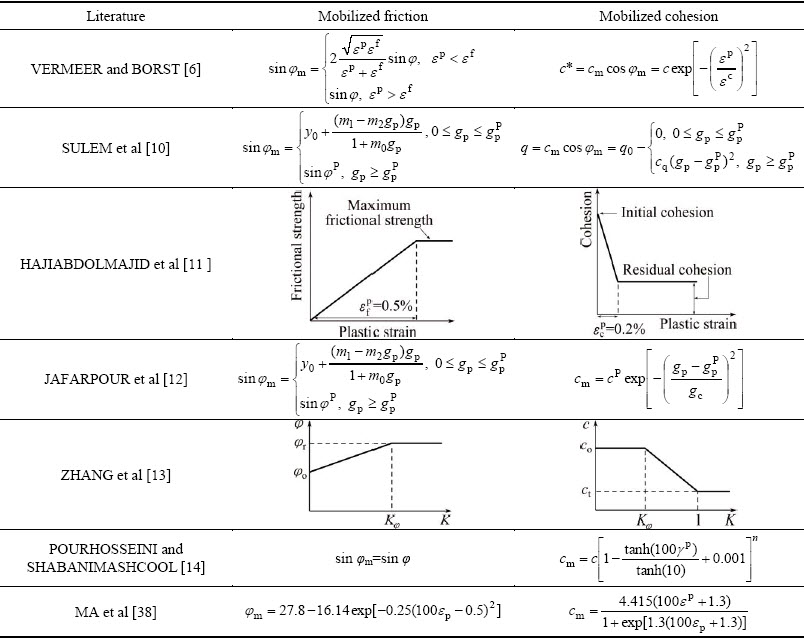
Note that the mobilized friction function sin φ_m in JAFARPOUR et al [12] is proposed by SULEM et al [10] and the function c^*_m is similar to VERMEER and BORST [6].

If the formulations in Table 1 are used to simulate tests on soft rock, they will produce poor results. Thus, it is necessary to propose a suitable hardening function for soft rock. Based on the results in Fig. 3, a hyperbolic equation is adopted to fit the mobilized friction sin φ_m as follows:

                    (10)

where φ_i is the mobilized friction angle at initial yield, and A and B are material constants, respectively.

For the mobilized cohesion , a hardening function is determined as a mixed parabolic equation and exponential equation:

      (11)

where  is the peak modified cohesion, i.e., the maximum cohesion, γ_cp is the effective plastic strain corresponding to peak modified cohesion , and a and γ_c are material constants, respectively. Note that the hardening function  proposed by VERMEER and BORST [6] is a special case of Eq. (11) when r_cp=0 and n=2.

Figure 8 shows the comparisons of the hardening functions (Eqs. (10) and (11)) with the experimental results. The hardening functions can predict the mobilization of strengths very accurately, which suggests that the proposed hardening functions are reasonable.

4.3 Plastic potential function

The non-associated plastic flow rule is adopted. Dilation is introduced into a plastic potential function to avoid excessively large dilatancies. The dilation is defined as changes in volume resulting from shear distortion of an element of materials. The plastic potential function differs from the yield function, but is formulated in analogy to the yield function, namely,

when ,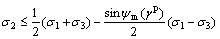

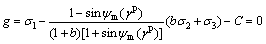 (12a)

when ,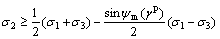

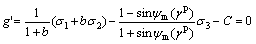   (12b)

where  is a mobilized angle of dilatancy. C is a constant. Similar to the yield function Eq. (8), the plastic potential function in terms of stress invariants can also be determined.

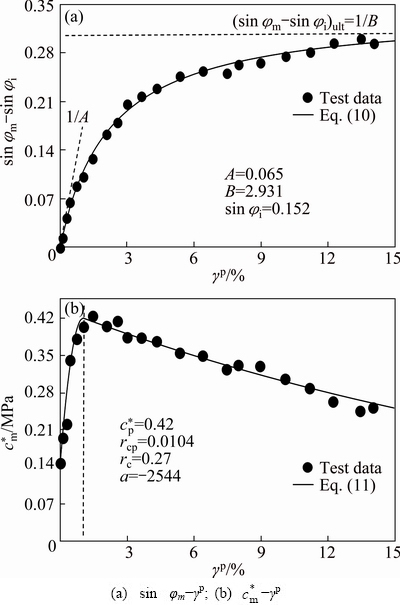
Fig. 8 Prediction of mobilized frictional and cohesive components for diatomaceous soft rock

It is clear that a constant dilatancy angle is not sufficient for this model to predict the behavior of soft rock. DETOURNAY [39], ZHAO and CAI [40] found the dependence of dilatancy angle on plastic strain and gave a equation to estimate the dilatancy angle. To determine the dilatancy angle, a stress-dilatancy relationship can be used, which not only defines the relationship between a friction angle and a dilation but also links a yield function and a yield potential function. ROWE [41] developed a stress dilatancy model that has been proved that it is accurate for sands. However, the model cannot be used in cohesive geomaterials. Thus, VERMEER and BORST [6] further modified the equation in different forms and obtained the more suitable form for cohesive geomaterials as

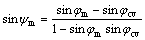                   (13)

where φ_cv is a constant. It is referred to as the “friction angle of constant volume”. The mobilized dilatancy angle is a function of plastic strain as the mobilized friction angle does. It is initially negative and increases with the increase of φ_m. The negative values must not be used for solid materials; instead ψ_m=0 can be useful for φ_m<φ_cv. Generally, the dilatancy angle is assumed to a constant artificially. However, from Eq. (13), it is clear that the dilatancy angle can be easily determined according to the friction angle. The excessive dilatancies can be avoided when predicting the mechanical behavior of materials.

4.4 Framework of elasto-plastic constitutive model

The total incremental strain is composed of the elastic and plastic incremental components

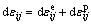                           (14)

The elastic strain increment is calculated by the generalized Hooke’s law, and the plastic strain increment is determined as

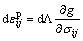                            (15)

where  is the plastic multiplier that is determined from the consistency condition df=0.

The elasto-plastic constitutive relationship can be represented as

                            (16)

where 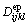 is the elasto-plastic stiffness matrix determined based on the yield function and plastic potential function

            (17)

where A is the hardening modulus, and

                        (18)

H is the proposed hardening functions Eqs. (10) and (11),  is the elastic matrix,

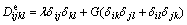            (19a)

                   (19b)

and λ, G, E, μ, and δ_ij are the Lame constant, shear modulus, elastic modulus, Poisson ratio and Kronecker delta, respectively.

4.5 Model parameters

There are 12 parameters needed to be determined in the proposed constitutive model. These parameters can be classified into the following three categories: elastic parameters, yield parameters and dilatancy parameters, and all of these except b can be obtained from conventional triaxial tests.

The elastic parameters include elastic modulus E and Poisson ratio μ which can be obtained directly from conventional tests. Many evidences have been illustrated that the elastic modulus E is dependent on confinement pressure. Herein, E suggested by JANBU [42] is adopted

                           (20)

where p_a is the atmospheric pressure, K is the modulus number, and m is the exponent constant that determines the rate of variation of E with σ₃. K and m can be determined from conventional triaxial tests by plotting E versus σ₃ on a lg-lg scale.

The yield parameters include the peak mobilized cohesion , plastic strain r_cp, initial mobilized friction angle φ_i, and constants b, n, a, r_c, A and B. Parameters , r_cp, a and r_c can be determined from the relationship of c^* and r^p shown in Fig. 8(b).  is the maximum cohesion at r^p=r_cp. a is obtained by plotting c^*_m-c^*_p versus (γ^p-γ_cp)². n and r_c are obtained from  versus ln γ^p. φ_i is directly obtained from Fig. 3 or Fig. 8(a). According to Eq. (10), A and B are obtained based on the following equation:

                    (21)

Actually, 1/A and 1/B are the initial tangent and asymptotic value of the hyperbola, respectively, as shown in Fig. 8(a).

5 Verification

The consolidated undrained triaxial tests of the diatomaceous soft rock in Fig. 1 are utilized to verify the proposed constitutive model. Table 2 lists the model parameters for the soft rock.

Table 2 Parameters of proposed constitutive model

Figure 9 shows the comparison of the proposed model prediction with the test data for the soft rock. The results indicate that the proposed constitutive model can reflect the strain softening of the soft rock and predict the experimental results well. Comparison with the ideal elastic-plastic constitutive model proposed by YU et al [30], the proposed constitutive model can reflect the strain softening behavior of materials. In addition, the strain hardening behavior can also be simulated, which will be discussed in the following. Furthermore, the proposed model can predict the whole stress-strain relationship better than the model in Ref. [15] due to the fact that the mobilization of cohesion component is considered.

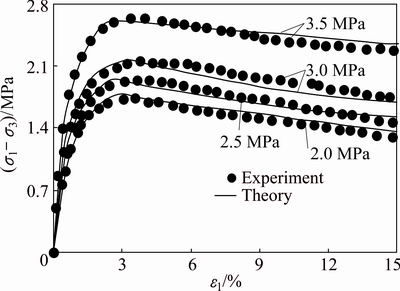
Fig. 9 Verification of proposed constitutive model

Singular points are formed at the intersections of the yield function/plastic potential function as shown in Fig. 5, which causes the flow vector not to be determined uniquely. For the conventional triaxial test, the Lode angle is equal to -30°. When 0≤b<1, the corners exist at θ_σ=-30°, where numerical difficulties will also be encountered. When b=1, due to the disappearance of corners, the flow vectors are determined uniquely. However, in this case, the mathematical overflow will be encountered. To overcome the singularities, the yield function for the explicit value θ_σ=-30° can be obtained.

       (22)

Analogy to the yield function, the singularity of the plastic function can also be solved. Note that parameter b has no effect on the predicted results under conventional triaxial conditions. This is because the yield function at θ_σ=-30° is independent of b as shown in Eq. (22) as well as the plastic potential function, which cause the flow vectors to be also independent of b.

Figure 10 shows the relationship between mobilized yield envelope and stress path of the soft rock. The slopes of yield envelope at different strain levels represent the change of the mobilized friction angle, and the intercept represents the change of mobilized cohesion. The changes of the cohesive and frictional components are identical with that in Fig. 3. The stress paths of σ₃=2.0 MPa and σ₃=3.5 MPa are plotted in Fig. 10. The strain softening behavior of the soft rock can also be illustrated by the relationship between stress path and strength envelope as shown in Fig. 6.

Fig. 10 Illustration of stress path and mobilization of strength

The dash line in Fig. 10 represents another type of stress path. If the stress path always increases, the strain hardening can be simulated by the proposed constitutive model. Figure 10 suggests that the occurrence of strain hardening or strain softening is not only decided by the stress level but also depends on strength component, i.e., the mobilized cohesion or the mobilized friction. All of the evidences clearly support that the proposed constitutive is a mixed hardening/softening constitutive model. However, herein, it should be noted that only the conventional undrained consolidated tests are available, so the verification for the tests of different stress paths cannot be conducted. The performance of the proposed constitutive model for different stress paths is only investigated theoretically.

The proposed constitutive model is developed by considering the unified strength theory. As mentioned above, the unified strength theory belongs to a three dimensional criterion and can form a series of strength criteria when b takes different values. So, the constitutive model has two advantages. One advantage is that the model can simulate the behavior under the complex stress state, the other is that materials can be modeled by selecting an appropriate b.

Due to the insufficiency of polyaxial test data for soft rock, we cannot investigate the effect of b and the intermediate principal stress σ₂ on stress strain relationship. For simplicity, these effects are examined by analyzing the change of friction angle under complex stress conditions. An equivalent friction angle and cohesion can be obtained based on the unified strength theory. Figure 11 shows the comparison of the equivalent friction angle with the friction angle reported by BISHOP [34] under the complex stress states. The results indicate that the equivalent friction angle agrees well with the experiment result. Thus, the comparison also suggests that the proposed constitutive model can reflect the effect of b and σ₂ on the mechanical behavior of materials.

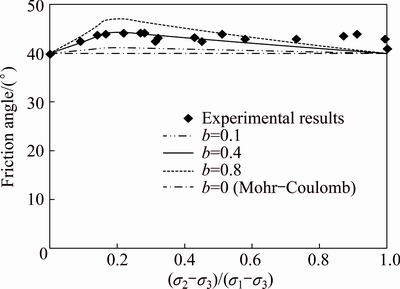
Fig. 11 Comparison of equivalent friction angle with experimental results reported by BISHOP [34]

6 Discussion

The above analysis indicates that the friction component of soft rock always increases during loading. However, some evidences show that the frictional components of some materials first increase to a peak value and then decrease gradually to a certain value with deformation [7,43]. Figure 12 shows the mobilization of strength of granite reported by MARTIN [7]. It is clear that the mobilization of friction is different from that of the soft rock and clay shown in Figs. 3 and 4.

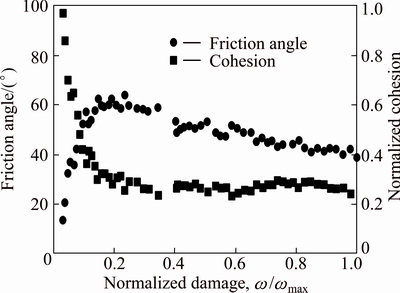
Fig. 12 Mobilzation of friction and cohesion of granite as function of damage (after MARTIN [7])

It is clear that the hardening function Eq. (10) cannot predict the friction angle in Fig. 12. We found that the mobilized friction angle in Fig. 12 can be expressed in terms of a hump function:

                (23)

where A, B and C are constants of material, which can be determined from conventional triaxial tests. Taking the derivative  results in the following equation:

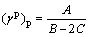                            (24)

Substitution of Eq. (24) into Eq. (23) gives

                       (25)

When the plastic strain tends to be infinite,

                            (26)

Figure 13 compares the experimental results with the theoretical results of Eq. (23). The results indicate that the hardening/softening function Eq. (23) agrees well with the experimental results.

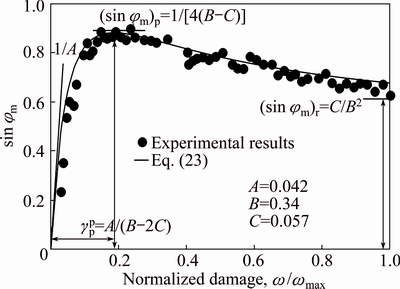
Fig. 13 Comparison of Eq. (23) with experimental results (test data after MARTIN [7])

Note that the hardening/softening function Eq. (23) will reduce to be the hardening function Eq. (10) when A=C. An extended constitutive model can be established by using the hardening/softening function Eq. (23) to replace the hardening function Eq. (10) and to be incorporated into the yield function Eq. (7) and the plastic potential function Eq. (12).

7 Conclusions

1) Based on the experiments of a diatomaceous soft rock, the mobilization of strength is investigated. The results indicate that the mobilized friction and cohesion of soft rock depend on plastic strain. A hyperbolic hardening function for the mobilized friction and a mixed parabolic and exponential equation for the mobilized cohesion are proposed. The hardening functions are illustrated by tests of soft rock.

2) A unified strength theory is introduced and verified by polyaxial tests of geomaterials. The results indicate that the unified theory is versatile and can reflect the effect of the intermediate principle stress.

3) In view of the unified strength theory and the mobilization of strength components, the yield function is given. The plastic potential function is determined by using the non-associated plastic flow rule. An elasto-plastic constitutive model is developed and verified. The results indicate that the proposed constitutive model can accurately predict the behavior of soft rock.

4) The proposed constitutive model describes not only the strain softening behavior but also the strain hardening of mateirals, which is decided by the stress level and the dominated strength component. The intermediate principal stress σ₂ and parameter b have significant effect on predicting the behavior of materials.

5) A hump hardening/softening function for mobilized friction is proposed to extend to a more generalized condition based on tests of other type rocks. The hyperbolic function is a special case of the hump function. A generalized constitutive model can be developed if the hump function is considered.

References

[1] ADACHI T, OKA F. An elasto-plastic constitutive model for soft rock with strain softening [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1995, 19: 233-247.

[2] ZHANG F, YASHIMA A, YE G L, ADACHI T, OKA F. An elastoplastic strain hardening and strain softening constitutive model for soft rock considering the influence of intermediate stress [J]. Soils and Foundations, 2003, 43(5): 107-117.

[3] ZHOU C Y, ZHU F X. An elasto-plastic damage constitutive model with double yield surfaces for saturated soft rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47: 385-395.

[4] FU Y, IWATA M, DING W, ZHANG F, YASHIMA A. An elastoplastic model for soft sedimentary rock considering inherent anisotropy and confining-stress dependency [J]. Soils and Foundations, 2012, 54(4): 575-589.

[5] LI Hang-zhou, LIAO Hong-jian, XIONG Guang-dong, HAN Bo, ZHAO Gui-ping. A three dimensional statistical damage constitutive model for geomaterials [J]. Journal of Mechanical Science and Technology 2015, 29(1): 71-77.

[6] VERMEER P A, de BORST R. Non-associated plasticity for soils, concrete and rock [J]. Heron, 1984, 29: l-64.

[7] MARTIN C D. The strength of massive Lac du Bonnet granite around underground openings [D]. Manitoba: University of Manitoba, Winnipeg, 1993.

[8] HAJIABDOLMAJID V. Mobilization of strength in brittle failure of rock [D]. Kingston, Ontario, Canada: Queen’s University, 2001.

[9] SCHMERTMANN J H, OSTERBERG J H. An experimental study of the development of cohesion and friction with axial strain in saturated cohesive soils [C]//Proceedings Research Conference on Shear Strength of Cohesive Soils. New York: ASCE, 1960: 643-694.

[10] SULEM J, VARDOULAKI, I. PAPAMICHOS E, OULAHNA A, TRONVOLL J. Elasto-plastic modeling of Red Wildmoor sandstone [J]. Mechanics of Cohesive-Frictional Materials, 1999, 4: 215-245.

[11] HAJIABDOLMAJID V, KASIER P K, MARTIN C D. Modelling brittle failure of rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39: 731-741.

[12] JAFARPOUR M, RAHMATI H, AZADBAKHT S, NOURI A, CHAN D, VAZIRI H. Determination of mobilized strength properties of degrading sandstone [J]. Soils and Foundations, 2012, 54(4): 658-667.

[13] ZHANG Kai, ZHOU Hui, SHAO Jian-fu. An experimental investigation and an elastoplastic constitutive model for a porous rock [J]. Rock Mechanics and Rock Engineering, 2013, 46: 1499-1511.

[14] POURHOSSEINI O, SHABANIMASHCOOL M. Development of an elasto-plastic constitutive model for intact rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 66: 1-12.

[15] LI Hang-zhou, LIAO Hong-jian, SONG Li, REN Jia-ning, LENG Xian-lun. Twin shear unified elastoplastic constitutive model considering strain softening behavior [J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(4): 720-728.

[16] LADE P V, MUSANTE H M. Three dimensional behavior of remolded clay [J]. Journal Geotechnical Engineering Division, ASCE, 1978, 104(2): 193-209.

[17] NAKAI T, MATSUOKA H, OKUNO N, TSUZUKI K. True triaxial tests on normally consolidated clay and analysis of the observed shear behavior using elastoplastic constitutive models [J]. Soils and Foundations, 1986, 26(4): 67-78.

[18] PRASHANT A, PENUMADU D. Effect of intermediate principal stress on overconsolidated kaolin clay [J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2004, 130(3): 284-292.

[19] KUMRUZZAMAN M, YIN J H. Influence of the intermediate principal stress on the stress–strain–strength behaviour of a completely decomposed granite soil [J]. Geotechnique 2012, 62(3): 275-280.

[20] YE G L, YE B, ZHANG F. Strength and dilatancy of overconsolidated clays in drained true triaxial tests [J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2014; DOI: 10.1061/(ASCE) GT.1943-5606.0001060.

[21] MOGI K. Experimental rock mechanics [M]. London: Taylor and Francis, 2007.

[22] MICHELIS P. Polyaxial yielding of granular rock [J]. Journal Engineering Mechanics, ASCE, 1985, 111(8): 1049-1066.

[23] HAIMSON B, CHANG C. A new true triaxial cell for testing mechanical properties of rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37: 285-296.

[24] CHANG C, HAIMSON B. True triaxial strength and deformability of the German Continental deep drilling program (KTB) deep hole amphibolites [J]. Journal Geophysical Research, 2000, 105: 18999-19013.

[25] DU Kun, LI Xi-bing, LI Di-yuan, WENG Lei. Failure properties of rocks in true triaxial unloading compressive test [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(2): 571-581.

[26] YU M H. Advances in strength theories for materials under complex stress state in the 20th century [J]. Applied Mechanics Reviews, 2002, 55(3): 169-218.

[27] LI H Z, LIAO H J, REN J N, XIONG G D, ZHAO G P, NING C M. Comparison of strength criteria of rock under complex stress state [C]//Proceedings of International Symposium on Geomechanics from Micro to Macro, Is-Cambridge, Cambridge, 2014: 715-720.

[28] YU M H. Unified strength theory and applications [M]. Berlin: Springer, 2004.

[29] YU M H, MA G W, QIANG H F, ZHANG Y Q. Generalized plasticity [M]. Berlin: Springer, 2007.

[30] YU M H, YANG S Y, FAN S C, MA, G W. Unified elasto-plastic associated and non-associated constitutive model and its engineering applications [J]. Computers and Structures 1999, 71: 627-636.

[31] LIAO Hong-jian, NING Chun-ming, YU Mao-hong, MASARU A, ZHAO Shu-de. Experimental study on strength deformation time relationship of soft rock [J]. Rock and Soil Mechanics, 1998, 19(2): 8-13.

[32] MARTIN C D. Seventeenth Canadian geotechnical colloquium: The effect of cohesion loss and stress path on brittle rock strength [J]. Canadian Geotechnical Journal, 1997, 34(5): 698-725.

[33] HANDIN J. On the Coulomb–Mohr failure criterion [J]. Journal Geophysical Research, 1969, 74: 5343-5348.

[34] BISHOP A W. Shear strength parameters for undisturbed and remoulded soil specimens [C]//Proc Roscoe Memorial Symp. Cambridge, 1972: 3-58.

[35] YU M H, HE L N. A new model and theory on yield and failure of materials under the complex stress state [C]//JONO M, INOUE T, editors. Mechanical Behaviour of materials-VI, (ICM-6). Oxford: Pergamon, 1991: 841-846.

[36] YU Mao-hong, HE Li-nan, SONG Ling-yu. Twin shear stress theory and its generalization [J]. Science in China Series A, 1985, 28(11): 1174-1183.

[37] YU Mao-hong, XIA Gui-yu, KOLUPAEV A V. Basic characteristics and development of yield criteria for geomaterials [J]. Journal Rock Mechanics and Geotechnical Engineering, 2009, 1(1): 71-88.

[38] MA L, XU H, TONG Q, DONG L, ZHANG N, LI J. Post-yield plastic frictional parameters of a rock salt using the concept of mobilized strength [J]. Engineering Geology, 2014, 177: 25-31.

[39] DETOURNAY E. Elastoplastic model of a deep tunnel for a rock with variable dilatancy [J]. Rock Mechanics and Rock Engineering, 1986, 19: 99-108.

[40] ZHAO X G, CAI M. A mobilized dilation angle model for rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47: 368-384.

[41] ROWE P W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact [C]//Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, London: 1962: 500-527.

[42] JANBU N. Soil compressibility as determined by oedometer and triaxial tests [C]//Proc Eur Conf Soil Mech Found Eng, Wiesbadem: 1963: 19-25.

[43] de SOUZA NETO E A, PERIC D, OWEN D R J. Computational methods for plasticity [M]. New York: John Wiley & Sons Ltd, 2008.

基于强度发挥的软岩弹塑性本构模型

李杭州¹，熊光东¹，赵桂平²

1. 西安交通大学 土木工程系，西安 710049；

2. 西安交通大学 航天航空学院，西安 710049

摘  要：在塑性力学的框架范围内研究弹塑性本构模型，分析软岩的强度变形特性。结果表明，软岩的黏聚力和内摩擦角是塑性应变的函数，在此基础上，提出双曲线型函数的发挥内摩擦角以及指数和多项式混合型的发挥黏聚力函数模型。基于统一强度理论和材料强度的发挥特性，确定软岩的屈服函数，采用非相关联流动法则确定塑性势函数，建立软岩的弹塑性本构模型并对其进行验证，结果表明所建立的本构模型可以较好地预测软岩的力学行为特性。分析所建立本构模型的优点，结果显示所建立的本构模型为硬化/软化混合型本构模型。进一步扩展更具有普遍性的硬化/软化驼峰型发挥内摩擦角函数。

关键词：本构模型；发挥强度参数；统一强度理论；软岩

(Edited by Yun-bin HE)

Foundation item: Projects (51279155, 51009114) supported by the National Natural Science Foundation of China; Project (xjj2014127) supported by the Fundamental Research Funds for the Central Universities, China

Corresponding author: Hang-zhou LI; Tel: +86-29-83395117; E-mail: lihangzhou77@163.com

DOI: 10.1016/S1003-6326(16)64173-0

Abstract: A new elasto-plastic constitutive model is presented in the framework of plasticity theory. The strength characteristics of a diatomaceous soft rock is investigated. The friction angle and cohesion of soft rock are mobilized as a function of plastic strain. A hyperbolic hardening function for the mobilized friction and a mixed parabolic and exponential equation for the mobilized cohesion are proposed. In view of the unified strength theory and the mobilizations of strength components, a yield function is given. A plastic potential function is determined by using the non-associated plastic flow rule. An elasto-plastic constitutive model is developed and verified. The results indicate that the proposed model can predict the behavior of soft rock accurately. The advantages of the proposed constitutive model are analyzed. The evidences support that the proposed constitutive model is a mixed hardening/softening model. A hump hardening/softening function for mobilized friction is extended to a more generalized condition.