DOI: 10.11817/j.issn.1672-7207.2018.06.016
具有混合时变时滞主从神经网络的指数采样同步控制
陈刚1, 2,王信1, 2,肖伸平1, 2,杜博文1, 2,王聪聪1, 2,罗昌胜1, 2
(1. 湖南工业大学 电气与信息工程学院,湖南 株洲,412007;
2. 电传动控制与智能装备湖南省重点实验室,湖南 株洲,412007)
摘 要:
变时滞的主从神经网络指数采样同步控制问题,运用Lyapunov-Krasovskii泛函方法以及线性矩阵不等式方法对其进行研究。通过构造新的增广Lyapunov-Krasovskii泛函,并对其导数采用一系列不等式方法进行界定,获得具有更小保守性的时滞相关指数同步判据。同时,基于最大采样间隔以及衰减率,得到可行控制器。最后,通过数值算例及仿真证明此方法的优越性以及可行性。
关键词:
主从神经网络;Lyapunov-Krasovskii泛函;指数采样同步控制;
中图分类号:TP273 文献标志码:A 文章编号:1672-7207(2018)06-1432-08
Sampled-data exponential synchronization of master-slave neural networks with time-varying mixed delays
CHEN Gang1, 2, WANG Xin1, 2, XIAO Shenping1, 2, DU Bowen1, 2, WANG Congcong1, 2,LUO Changsheng1, 2
(1. School of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou 412007, China;
2. Key Laboratory for Electric Drive Control and Intelligent of Hunan Province, Zhuzhou 412007, China)
Abstract: Sampled-data exponential synchronization problems for master-slave neural networks with time-varying mixed delays were investigated with the Lyapunov-Krasovskii functional approach and linear matrix inequality(LMI).By constructing the novel Lyapunov-Krasovskii functions and estimating the derivative of them with a set of inequality methods, exponential synchronization criteria with time-varying delays were derived, which had less conservative. Then, depending upon the maximum sampling interval and decay rate, the desired sampled-data controller was achieved. The numerical example and simulation results verify the superiority and effectiveness of the approach.
Key words: master-slave neural networks; Lyapunov-Krasovskii function; sampled-data exponential synchronization
神经网络(neural networks)已经广泛运用于各种工程领域,如模式识别、静态图像处理、联想储存以及组合优化等[1-5]。神经网络在大规模综合电子回路的实现过程中,神经元之间的信息交互往往会产生神经元时滞现象。而此时滞往往是导致系统震荡、发散和不稳定的重要原因,因此,对时滞相关神经网络的研究具有实际与理论意义。系统中的时滞项存在许多形式,常见的有离散时滞与分布时滞。在研究时滞系统的方法中,Lyapunov-Krasovskii泛函方法以及线性矩阵不等式方法(LMI)得到广泛运用。例如,在对时滞系统稳定性的研究中,利用Lyapunov-Krasovskii泛函方法构建Lyapunov增广泛函,并对其导数进行界定,可以得到线性矩阵不等式形式的稳定性判据。至今已有许多稳定性判据被推导[6-9]。同样,在对时滞神经网络的无源性、耗散性、全局稳定性、指数稳定性以及同步性等的研究中,推导出大量线性矩阵不等式形式的判据[10-11]。基于Lyapunov稳定性定理,可从2个方面获得更低保守性判据:一个是构建更加合适的Lyapunov-Krasovskii泛函,另一个是利用更好的不等式界定方法,界定泛函中的交叉项。在构建Lyapunov-Krasovskii泛函时,大多采用增广泛函方法[1-6]。而在研究界定交叉项时,主要采用自由权矩阵方法[11] 、积分不等式方法[12]以及凸优化方法[13]等。近年来,同步控制问题[14]被广泛研究,包括时滞反馈控制、自适应控制、模糊控制、脉冲控制以及采样控制在内的控制方法被运用于同步控制问题中。主、从神经网络同步控制同样可以利用这些控制方法,如ZHANG等[15-17]基于线性矩阵不等式方法以及Lyapunov-Krasovskii泛函方法对混合时滞主从神经网络指数采样同步控制进行了研究,得到1个控制该神经网络同步的线性矩阵不等式判据以及可行控制器。本文作者在文献[16]的基础上,研究具有离散与分布时滞的主从神经网络指数采样同步控制问题,构建新的增广Lyapunov-Krasovskii泛函。对泛函导数进行估计,获得具有更小保守性的指数同步性判据以及可行控制器,并通过数值计算以及仿真结果证明该方法的优越性和可行性。
1 问题描述
采用如下标号:矩阵上标“T”和“-1”分别表示转置矩阵以及逆矩阵;Rn和Rn×n分别代表n维向量和n×n维矩阵;矩阵P>0代表矩阵P是正定的;diag{b1,…,bn}表示块对角矩阵;0和I分别表示合适维度的零矩阵以及合适维度的单位矩阵;Sym{P}代表矩阵PT+P;标记“*”表示块对阵矩阵中的对称项。
考虑下面的混合时滞神经网络:
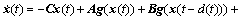
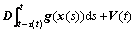 (1)
(1)
其中:x(t)=[x1(t),x2(t),…,xn(t)]T∈Rn,为t时间神经元状态向量;g(t)=[g1(t),g2(t),…,gn(t)]T∈Rn,为神经元激励函数向量,且有g(0)=0;C=diag{a1,…,an},是1个正定对称矩阵;A=(aij)n×n,B=(bij)n×n,D=(dij)n×n,表示连接权矩阵;V(t)=[V1(t),…,Vn(t)]T,为外部输入向量;d(t)和τ(t)分别表示离散时滞与分布时滞,并且满足以下条件:
(C1) 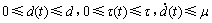 ;
;
(C2) 
其中:d ,τ和μ都为常数。
假设1[16]:系统(1)中的激励函数gi(·)是连续的且满足
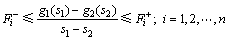 (2)
(2)
其中:S1≠S2;Fi-和 Fi+为已知实恒定值。
设定系统(1)是主系统,则系统(1)的从系统可以写成以下形式:
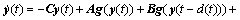
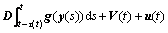 (3)
(3)
其中:C,A,B和D与系统(1)中等价;u(t) ∈ Rn,为合适的控制输入。
据文献[1-5],通过定义误差信号为r(t)=y(t)-x(t),误差系统可以写成以下形式:
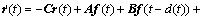
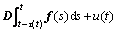 (4)
(4)
其中:f (t) = g (y(t))-g (x(t))。必须指出的是,f (t)依赖于y(t)和x(t),这里用f (t)代替f (x(t),y(t))。
假设控制信号由零阶保持函数发生,其保持以下时间次序:
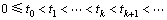
则状态反馈控制器可以写成以下形式:
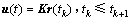 (5)
(5)
其中:K为采样反馈控制增益矩阵;tk 为第k个采样时间,且满足当k趋向于无穷大时,tk 也趋向无穷大;r(tk)表示tk采样时刻状态向量r(t)的离散值。
 (6)
(6)
其中:h为正标量,代表最大采样间隔。
将(5)代入系统(4),可以得到下面误差系统:
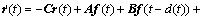
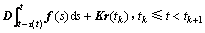 (7)
(7)
这里,引入指数同步性的概念。
注释1:设mk=t-tk,mk+1=tk+1-t,据式(6)可以得出在系统(7)中,有0≤mk<h,0<mk+1≤h。又因为mk和mk+1是关于t的一次函数,所以,有

或者
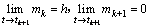
定义1:若误差系统(7)是指数稳定的,则主系统(1)与从系统(3)指数同步。换言之,存在2个常数 ρ>0,α>0,
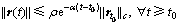 (8)
(8)
其中: 。
。
引理1[17]:对于所有对称正定矩阵X及可积函数{w(s) | s ∈ [α, β]},满足
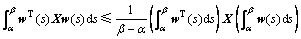
引理2[18]:对于任意向量w1和 w2,正定对称矩阵X,任意合适矩阵S以及标量β∈(0,1),当条件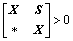 成立时,有
成立时,有
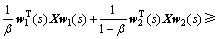
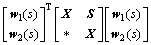
引理3[19]:对于任意正定对称矩阵X,2个标量β>α>0以及可积函数w(s),有

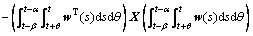
引理4[17]:存在合适维度的矩阵Ω1,Ω2和Ω3,其中Ω1是对称矩阵,Ω2是对称正定矩阵,则有
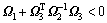
当且仅当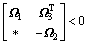 或者
或者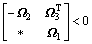 时成立。
时成立。
2 主要结果
定义:
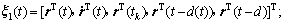
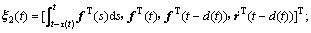
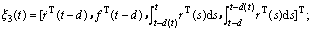
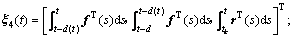
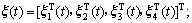

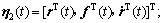
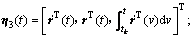
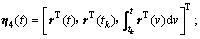
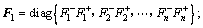

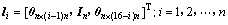 ;
;
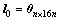 。
。
定理1:在条件(C1)下,给定正常数d和τ以及常数γ和μ,若存在正定对称矩阵P∈Rn×n,Pa∈R2n×2n,Pb∈Rn×n,Qi∈R3n×3n (i=1, 2),Z1∈R3n×3n,Zi∈Rn×n(i=2,3,4),M∈Rn×n,U∈R3n×3n,对称阵Yi∈Rn×n(i=1,2),X5∈Rn×n,正定对角阵Vi∈Rn×n(i=1,2),以及任意矩阵O∈R2n×2n,H∈R3n×5n,Xi∈Rn×n(i=1,2,3,4),G∈Rn×n,L∈Rn×n,且有以下矩阵不等组成立:
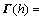
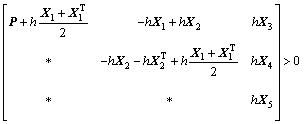 (9)
(9)
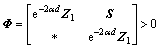 (10)
(10)
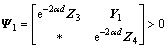 (11)
(11)
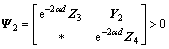 (12)
(12)
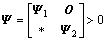 (13)
(13)
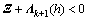 (14)
(14)
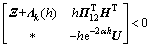 (15)
(15)
其中:
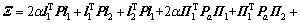
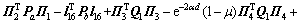
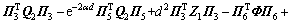

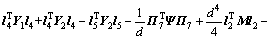
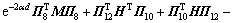
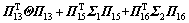 ;
;
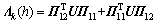 ;
;
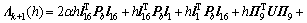
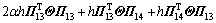 ;
;
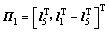 ;
;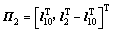 ;
;
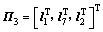 ;
;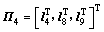 ;
;
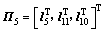 ;
;
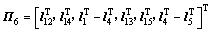 ;
;
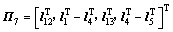 ;
;
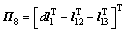 ;
;
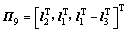 ;
;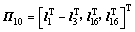 ;
;
 ;
;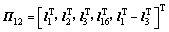 ;
;
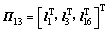 ;
;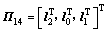 ;
;
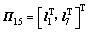 ;
;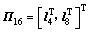 ;
;
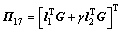 ;
;
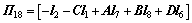 ;
;
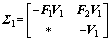 ;
;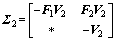 ;
;
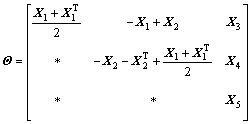 。
。
则主系统(1)与从系统(3)是指数同步的,其衰减率为α。另外,据系统(7)中的可行控制增益矩阵求得K=G-1L。
证明:构建下面的增广泛函:
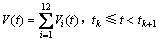 (16)
(16)
其中:
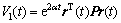 ;
;
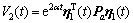 ;
;
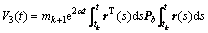 ;
;
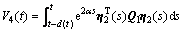 ;
;
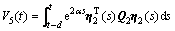 ;
;
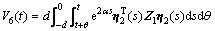 ;
;
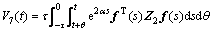 ;
;
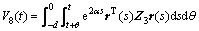 ;
;
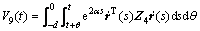 ;
;
 ;
;
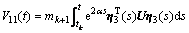 ;
;
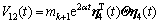 。
。
对V(t)求导,可得
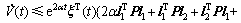
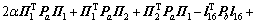

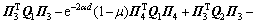
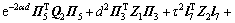
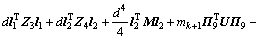



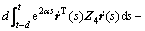
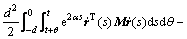
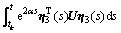 。
。
根据引理1和引理2,可知
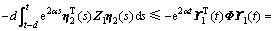
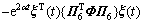
其中: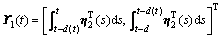 。
。
根据引理1,可知
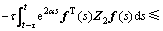
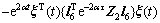
这里,引入2个零项等式:
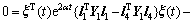
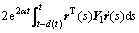 (17)
(17)
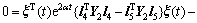
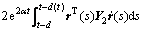 (18)
(18)
又根据引理1和引理2,并将式(17)和(18)中的积分项代入,根据文献[8]中的推理,可得
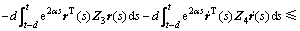
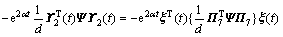
其中:
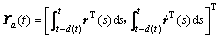 ;
;
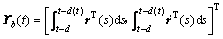 ;
;
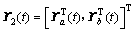 。
。
由引理3,可得

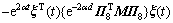
运用自由权矩阵方法,对任意适合维度的自由矩阵H,有下面的不等式成立:
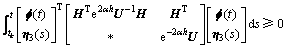
其中:
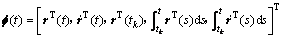 。
。
故可得
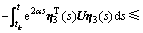
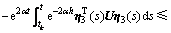
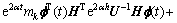

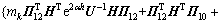

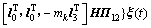 。
。
根据误差系统(7),对于任意合适的矩阵G,L以及标量γ,有
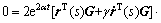
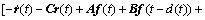
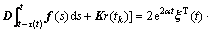
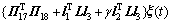
同时,根据不等式(2),对于任意i=1,2,…,n,有
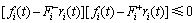
对于合适维度的正定对角矩阵V1和V2,可得
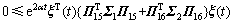
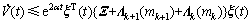 (19)
(19)
根据引理4,式(14)和(15)等同于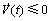 ,t∈[tk, tk+1)。
,t∈[tk, tk+1)。
根据文献[16],当P>0以及式(9)成立时,存在充分小的正标量δ和σ,有
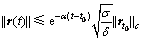 (20)
(20)
因此,系统(7)是指数稳定的,其衰减率为α。根据定义1,主系统(1)与从系统(3)是指数同步的。其指数同步率为α。证毕。
注释2: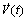 无法直接用Matlab计算。由计算结果以及注释1,已知
无法直接用Matlab计算。由计算结果以及注释1,已知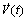 是关于mk或mk+1的一次函数,因此,求解
是关于mk或mk+1的一次函数,因此,求解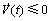 ,等同于求
,等同于求
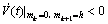 ,
,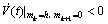
其结果见式(14)与(15)。
注释3:引理2中β的取值并不影响时滞d(t)的取值,因此,d(t)可以等于0或者d。
定理2:在条件(C2)下,给定正常数d 和τ以及常数γ和μ,若存在正定对称矩阵P∈Rn×n,Pc∈R4n×4n,Pb∈Rn×n,Qi∈R3n×3n (i=1, 2),Z1∈R3n×3n,Zi∈Rn×n(i=2,3,4),M∈Rn×n,U∈R3n×3n ,对称阵Yi∈Rn×n(i=1,2),X5∈Rn×n,正定对角阵Vi∈Rn×n(i=1,2),以及任意矩阵O∈R2n×2n,H∈R3n×5n,Xi∈Rn×n(i=1,2,3,4),G∈Rn×n,L∈Rn×n,且有下面不等式组成立:
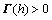 ,
,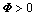 ,
,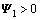 ,
,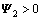 ,
,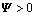
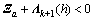 ,
,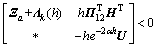
其中:Γ(h),Φ,Ψ1,Ψ2,Ψ,Ξ,Π1,Π2和Pa在定理1中定义,且
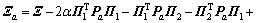
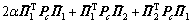 ;
;
 ;
;
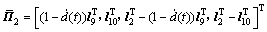 。
。
则主系统(1)与从系统(3)是指数同步的。另外,据系统(7)中的可行控制增益矩阵求得K=G-1L。
证明:构建以下增广泛函:
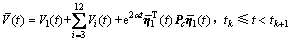
其中:V1(t),Vi (t)(i=3,…,12)在定理1中被定义。同理,可以证明定理2的结论。
注释4:在条件(C2)下,无法直接用Matlab计算。因为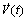 对
对 是一次函数,所以,可同时计算
是一次函数,所以,可同时计算 =-μ和
=-μ和 =μ时的2种条件。
=μ时的2种条件。
当系统没有分布时滞时,神经网络(1)和(3)可以写成下列形式:
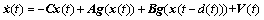 (21)
(21)
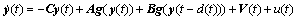 (22)
(22)
同样地,误差系统(4)可写成
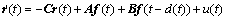 (23)
(23)
根据定理1与定理2,并将增广泛函中的V7(t)去掉,可以得到下面2个定理。
定理3:在条件(C1)下,给定正常数d以及常数γ和μ,若存在正定对称矩阵P∈Rn×n,Pa∈R2n×2n,Pb∈Rn×n,Qi∈R3n×3n (i=1, 2),Z1∈R3n×3n,Zi∈Rn×n(i=3,4),M∈Rn×n,U∈R3n×3n ,对称阵Yi∈Rn×n(i=1,2),X5∈Rn×n,正定对角阵Vi∈Rn×n(i=1,2),以及任意矩阵O∈R2n×2n,H∈R3n×5n,Xi∈Rn×n(i=1,2,3,4),G∈Rn×n,L∈Rn×n,且有下面不等式组成立:
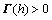 ,
,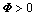 ,
,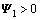 ,
,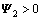 ,
,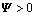 ;
;
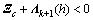 ,
,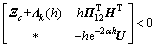
其中:Γ(h),Φ,Ψ1,Ψ2,Ψ,Ξ,Z2和τ在定理1中被定义,且
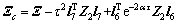 。
。
则主系统(21)与从系统(22)是指数同步的,其衰减率为α。另外,系统(23)中的可行控制增益矩阵求得为K=G-1L。
定理4:在条件(C2)下,给定正常数d以及常数γ,μ,如果存在正定对称矩阵P∈Rn×n,Pc∈R4n×4n,Pb∈Rn×n,Qi∈R3n×3n (i=1, 2),Z1∈R3n×3n,Zi∈Rn×n(i=3,4),M∈Rn×n,U∈R3n×3n ,对称阵Yi∈Rn×n(i=1,2),X5∈Rn×n,正定对角阵Vi∈Rn×n(i=1,2),以及任意矩阵O∈R2n×2n,H∈R3n×5n,Xi∈Rn×n(i=1,2,3,4),G∈Rn×n,L∈Rn×n,且有下列不等式组成立:
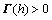 ,
,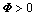 ,
,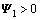 ,
,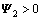 ,
,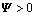
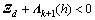 ,
,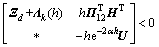
其中:Γ(h),Φ,Ψ1,Ψ2和Ψ在定理1中被定义,Ξa,Z2和τ在定理2中被定义,且
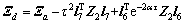
则主系统(21)与从系统(22)是指数同步的,其衰减率为α。另外,系统(23)中的可行控制增益矩阵求得,为K=G-1L。
3 仿真实例
例1 考虑系统主系统(1)与从系统(3)以及下列参数:
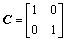 ,
,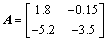 ,
,

假设d=1,τ=0.5,γ=0.15,μ=0.25,F1-= F2-=0和F1+= F2+=1。利用定理1与定理2,得到在不同采样间隔h下的最大允许α,其计算结果见表1。与文献[15]和文献[16]中结果相比,可知本文方法具有更小的保守性。
利用定理2,当h=0.1,α=0.796 7时,利用Matlab工具箱可以计算得到1个可行增益控制器:
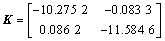
表1 例1中不同h下的最大允许α
Table 1 Maximum allowed α for different h in Example 1
例2 考虑系统主系统(21)与从系统(22)以及下列参数:
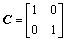 ,
,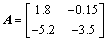 ,
,
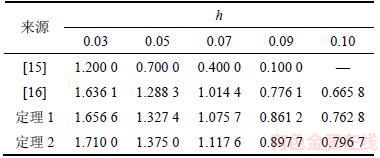
假设激励函数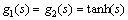 ,以及d=1,τ=0.5,γ=0.15,μ=0.25,F1-= F2-=0和F1+= F2+=1,利用定理3与定理4,得到在不同采样间隔h下的最大允许α,其计算结果见表2。与文献[16]对比,可知本文方法具有更小的保守性。
,以及d=1,τ=0.5,γ=0.15,μ=0.25,F1-= F2-=0和F1+= F2+=1,利用定理3与定理4,得到在不同采样间隔h下的最大允许α,其计算结果见表2。与文献[16]对比,可知本文方法具有更小的保守性。
利用定理4,当h=0.1,α=0.807 6,离散时滞d(t)=(et/ et+1),初始状态为x(t)=[0.6,0.7]T,y(t)=[0.8,0.5]T,t∈[-1,0]时,可以得到1个可行增益控制器:
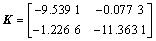
无控制输入时的状态轨迹见图1。根据上面的增益控制器,控制输入(5)以及误差系统(23)的响应曲线分别见图2和图3。从图2和图3可见:主系统(21)与从系统(22)在该控制器下是同步的。
表2 例2中不同h下的最大允许α
Table 2 Maximum allowed α for different h in Example 2
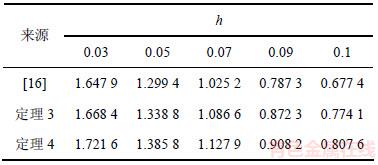
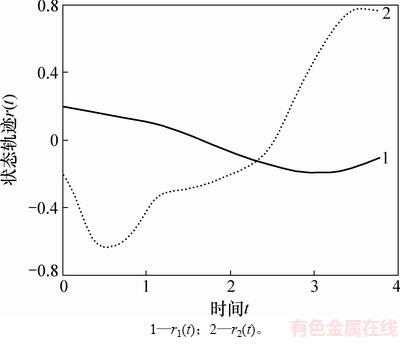
图1 例2中无控制输入误差系统(23)的状态响应
Fig. 1 State response of error system (23) without control input in Example 2
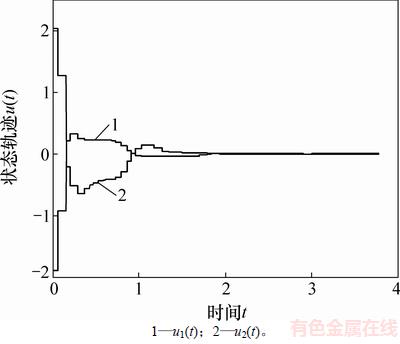
图2 例2中控制输入u(t)与时间t的关系
Fig. 2 Relationship between control input u(t) and time in Example 2
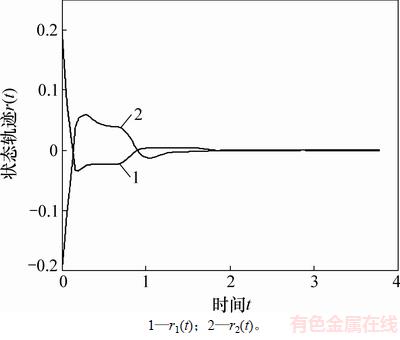
图3 例2中误差系统(23)的状态响应
Fig. 3 State responses of error system (23) in Example 2
4 结论
1) 运用神经网络建模,并将其与计算机系统相结合,能够解决很多工程领域的难题,如模式识别问题、联想储存、工程优化问题等。
2) 利用Lyapunov-Krasovskii泛函方法以及构建新的增广泛函,得到具有更小保守性的线性矩阵不等式形式的指数同步控制判据。并且通过比较系统在 (C1)与(C2)2种情况下的最大允许时滞,当考虑到更多时滞信息的情况下,所获得的稳定性判据具有更小的保守性。数值算例及仿真结果证明了此方法的优越性与可行性。
参考文献:
[1] YU Jianjiang, ZHANG Kanjian, FEI Shumin. Improved results on passivity analysis of discrete-time stochastic neural networks with time-varying delay[J]. Journal of Central South University (Science and Technology), 2009, 40(Z1): 63-67.
[2] BAI Yonggiang, CHEN Jie. New stability criteria for recurrent neural networks with interval time-varying delay[J]. Neurocomputing, 2013, 121(18): 179-184.
[3] GE Chao, HUA Changchun, GUAN Xinping. New delay-dependent stability criteria for neural networks with time-varying delay using delay-decomposition approach[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(7): 1378-1383.
[4] ZHANG Chuanke, HE Yong, JIANG Lin, et al. Delay-dependent stability criteria for generalized neural networks with two delay components[J]. IEEE Transactions on Neural Networks & Learning Systems, 2014, 25(7): 1263-1276.
[5] ZHANG Chuanke, HE Yong, JIANG Lin, et al. Delay-dependent stability analysis of neural networks with time-varying delay:a generalized free-weighting-matrix approach[J]. Applied Mathematics & Computation, 2017, 294(C): 102-120.
[6] ZENG Hongbing, HE Yong, WU Min, et al. Free-matrix-based integral inequality for stability analysis of systems with time-varying delay[J]. IEEE Transactions on Automatic Control, 2015, 60(10): 2768-2772.
[7] RAJA R, ZHU Quanxin, SENTHILRAJ S, et al. Improved stability analysis of uncertain neutral type neural networks with leakage delays and impulsive effects[J]. Applied Mathematics & Computation, 2015, 266(C): 1050-1069.
[8] ZENG Hongbing, HE Yong, WU Min, et al. Stability analysis of generalized neural networks with time-varying delays via a new integral inequality[J]. Neurocomputing, 2015, 161(C): 148-154.
[9] FATTAHI M, VASEGH N, MOMENI H R. Stabilization of a class of nonlinear discrete time systems with time varying delay[J]. Journal of Central South University (Science and Technology), 2014, 21(10): 3769-3776.
[10] WANG Xin, SHE Kun, ZHONG Shouming, et al. New result on synchronization of complex dynamical networks with time-varying coupling delay and sampled-data control[J]. Neurocomputing, 2016, 214: 508-515.
[11] WU Ming, LIU Fang, SHI Peng, et al. Exponential stability analysis for neural networks with time-varying delay[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society, 2008, 38(4): 1152-1156.
[12] XIAO Shenping, ZHANG Xianming. New globally asymptotic stability criteria for delayed cellular neural networks[J]. IEEE Transactions on Circuits & Systems II Express Briefs, 2009, 56(8): 659-663.
[13] KWON O M, JU H P. New delay-dependent robust stability criterion for uncertain neural networks with time-varying delays[J]. Applied Mathematics & Computation, 2008, 205(1): 417-427.
[14] YU Wenwu, CAO Jinde. Synchronization control of stochastic delayed neural networks[J]. Physica A Statistical Mechanics & Its Applications, 2007, 373(1): 252-260.
[15] ZHANG Chuanke, HE Yong, WU Min. Exponential synchronization of neural networks with time-varying mixed delays and sampled-data[J]. Neurocomputing, 2010, 74(1/2/3): 265-273.
[16] WU Zhengguang, SHI Peng, SU Yonghe, et al. Exponential synchronization of neural networks with discrete and distributed delays under time-varying sampling[J]. IEEE Transactions on Neural Networks & Learning Systems, 2012, 23(9): 1368-1376.
[17] RAKKIYAPPAN R, LATHA V P, ZHU Quanxin, et al. Exponential synchronization of Markovian jumping chaotic neural networks with sampled-data and saturating actuators[J]. Nonlinear Analysis Hybrid Systems, 2017, 24: 28-44.
[18] PARK P G, LEE W I, LEE S Y. Auxiliary function-based integral inequalities for quadratic functions and their applications to time-delay systems[J]. Journal of the Franklin Institute, 2015, 352(4): 1378-1396.
[19] KWON O M, JU H P, LEE S M. New augmented Lyapunov-Krasovskii functional approach to stability analysis of neural networks with time-varying delays[J]. Nonlinear Dynamics, 2014, 76(1): 221-236.
(编辑 陈灿华)
收稿日期:2017-07-12;修回日期:2017-09-20
基金项目(Foundation item):湖南省自然科学基金项目(2018JJ4075);国家自然科学基金资助项目(61672225,61304064)(Project(2018JJ4075) supported by the Natural Science Foundation of Hunan Province; Projects(61672225, 61304064) supported by the National Natural Science Foundation of China)
通信作者:陈刚,博士,副教授,从事时滞系统,鲁棒控制研究;E-mail:drchengang@163.com
摘要:对于具有混合时变时滞的主从神经网络指数采样同步控制问题,运用Lyapunov-Krasovskii泛函方法以及线性矩阵不等式方法对其进行研究。通过构造新的增广Lyapunov-Krasovskii泛函,并对其导数采用一系列不等式方法进行界定,获得具有更小保守性的时滞相关指数同步判据。同时,基于最大采样间隔以及衰减率,得到可行控制器。最后,通过数值算例及仿真证明此方法的优越性以及可行性。


