电弧炉电极调节系统的反馈线性化鲁棒控制
高媛，刘小河，史述东
(北京信息科技大学 自动化学院，北京，100192)
摘 要：
调节系统的反馈线性化鲁棒控制问题。应用微分几何的线性反馈方法对电弧炉电极调节系统的非线性部分进行处理，并在此基础上设计鲁棒控制器，进行MATLAB数字仿真。仿真结果表明，反馈线性化鲁棒控制具有更快的跟踪性能，超调量较小，比PID和单纯的反馈线性化控制效果好。
关键词：
中图分类号：TP273 文献标志码：A 文章编号：1672-7207(2011)S1-0228-05
Feedback linearization robust control of
arc furnace electrode regulator system
GAO Yuan, LIU Xiao-he, SHI Shu-dong
(School of Automation, Beijing Information Science and Technology University, Beijing 100192, China)
Abstract: The method of feedback linearization robust control for arc furnace electrode regulator system is discussed. With the linear feedback method of differential geometry dealing with non-linear part of electric arc furnace system, the controller was designed, and several simulations was done. Simulation results show that the feedback linearization robust control has shorter response time and smaller overshoot than the PID control and simplex feedback linearization control have.
Key words: arc furnace electrode regulator; feedback linearization; robust control
电弧炉是一种利用电弧作为热源的炉子，是目前应用的最为普遍的一种炼钢方法。电弧炉系统是一个多变量、非线性、强耦合的时变系统，随机干扰严重。因此，如何通过电极调节系统控制合适的弧长并使之稳定，是电弧炉控制系统的重要研究方面。近年来，很多学者将智能控制等方法应用于电弧炉电极调节系统中，且已取得了一定成果，但是由于先验知识的缺乏，从而导致控制效果需要在实际应用中进行进一步的改进[1-2]。反馈线性化鲁棒控制是将反馈线性化的控制方法和鲁棒结合，形成的一种混合控制方法。其基本思想是通过适当的非线性状态反馈和非线性坐标变换，将一个非线性系统变换成为一个线性系统，然后再对系统加入鲁棒控制器，改善系统性能，增强系统的鲁棒性。本文作者将这种控制方法应用到电弧炉电极调节系统中，有效地克服了不确定性干扰对系统的影响，使系统的动静态品质得到了进一步提升。
1 电弧炉电极调节系统的描述
电弧炉电极调节系统可以用一个非线性传递算子来描述其动态特性。其中，电极调节器可用线性传递函数描述，电弧炉主电路可由一组非线性状态方程来描述。对于单相电弧炉系统，可以把电弧炉主电路视为将电弧弧长映射为电弧电流的非线性环节，即
(1)
其中：I为电弧电流有效值；L为电弧弧长。电弧炉调节器系统框图如图1所示。图中放大器、电机、测速反馈以及减速器为线性系统。
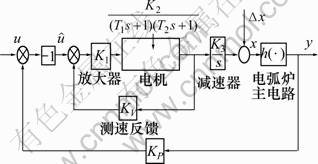
图1 单相电弧炉电极调节系统方框图
Fig.1 Block diagram of simple-phase arc furnace electrode regulation system
由图1得系统微分方程为
(2)
令
，
，
，
，
，
则
，
，
。
即电弧炉系统可描述为如下仿射系统的形式
(3)
其中：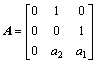
，
。
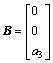2 电弧炉电极调节系统的反馈线 性化
2.1 单输入单输出系统的反馈线性化
对于如下单输入单输出系统：
(4)
式中，
是n维向量；f(x)和g(x)为n维光滑向量函数；u和y为标量；h(x)为标量函数。当系统(4)的相对阶与系统的阶数相同时，系统可以精确反馈线性化。存在状态反馈公式
把输入输出简化为
，式中，ρ为阶数，v为反馈控制信号。
2.2 电弧炉系统的反馈线性化
对于系统(3)，求Lie导数可得：系统相对阶r=3，与系统阶数n相同，所以电弧炉电极调节系统可以精确反馈线性化。
令
，
，
，则反馈线性化中的状态反馈线性化律为：
(5)
那么，可以将原非线性系统变换为线性系统：
(6)
式(6)可写作：
，
其中，
，
，
。
3 电弧炉电极调节系统鲁棒控制
3.1 不确定非线性系统的鲁棒控制
对于如下不确定非线性系统
(7)
其中：
为系统的状态变量； 
，
分别是系统的输入向量及输出；?f(x)和?g(x)分别是系统的状态不确定性及输入不确定性；f(x)，?f(x)，g(x)和?g(x)是光滑向量场。
假设1 系统(7)的不确定性满足匹配条件即存在光滑函数D(x): Rn→Rm，E(x): Rn→Rm×m使得对
，有?f(x)=G(x)D(x)，
。根据文献[3]，设系统输入变换为
，N为维数适合的矩阵且其逆矩阵存在，那么，系统(7)可进行线性化变换，并且线性化控制律为
(8)
令
，定义误差向量
，其中各分量是
根据线性化律(8)，可以写出系统(7)的误差动态方程是
(9)
由于(M, N)能控，则存在反馈阵
，
，使矩阵M-NK的特征根均具有负实部。
假设2 对于
，存在非负连续函数
ρ1(x)和ρ2(x)，
(10)
(11)
其中，||·||表示Rm空间的2范数；||·||ico表示Rm×m空间的无穷范数。
为了使系统输出y按照指数规律跟踪期望输出yd及其补偿不确定性对系统的影响，按照补偿原理设计的控制信号v分为以下2个部分
(12a)
(12b)
(12c)
其中，
，ε和α是给定的常数，ε >0，
；
是矩阵P的最大特征值；P是正定对称阵，为如下李雅普诺夫方程的解
(13)
结论[4]：如果不确定非线性系统(7)满足假设1和假设2，那么在控制律(8)和(12)的作用下，输出y按照指数规律跟踪期望输出yd。
3.2 电弧炉系统的鲁棒控制
在电弧炉电极调节系统存在弧长干扰的情况下，假设弧长干扰为?x (有界且相对于x1比较小)，它随时间可变。将干扰代入式子(3)可知：
(14)
整理可得：
(15)
令
，
，
，则系统可记作：
(16)
在理论研究中，用
近似电弧炉主电路，其与实际系统模型还存在一定的误差，可将这个误差和上述电弧炉系统的弧长干扰dx一起考虑，看作系统的不确定性，记作?f(x)，则电弧炉电极调节系统可表示为如下式子
(17)
其中：误差
。
因为
，
，所以，可得
。与标称系统(7)对比，可知
。这样，式(12)中的控制信号为：
(18)
(19)
在以上控制律作用下，输出y可以按照指数规律跟踪期望输出yd。
4 仿真研究
下面以单相电弧炉电极调节系统的控制为例，来验证上述反馈线性化鲁棒控制的应用效果。调节器的任务是对于给定电弧电流，能迅速调节电机使电机升降以得到合适的电弧弧长L，从而获得合适的电弧电流以熔炼金属。电弧炉电极调节系统(图1)中的参数值如下：K1=30.49，K2=2.45，K3=0.038，T1+T2=0.172，T1T2=0.000 425，KV=0.05，KP=1。
参考三阶系统传函为
。
选取c0=19 000，c1=2 900，c2=45。
设正定对称矩阵为P，代入李雅普诺夫方程
，可以求得：
，
，α=2，ε =0.01，
因此，
仿真过程中用来近似主电路部分。
给系统加入阶跃信号和方波信号的仿真结果如图2和图3所示。由图2和图3可以看出：反馈线性化鲁棒控制比单纯的反馈线性化控制的调节时间短，超调量较小。给系统加入白噪声干扰，仿真结果如图4所示。由图4可以看出：反馈线性化鲁棒控制的抗干扰能力比PID和单纯的反馈线性化控制效果要好。
图2 阶跃响应仿真结果
Fig.2 Simulated result of step response
图3 方波响应仿真结果
Fig.3 Simulated result of square-wave response
图4 存在白噪声干扰时各种控制方法对比
Fig.4 Comparison of different control methods by adding white noise
5 结论
针对电弧炉电极调节系统这一非线性系统，采用了反馈线性化的方法处理系统的非线性部分，并设计了鲁棒控制器，当系统存在较小干扰时可以有效地抑制干扰，优化系统性能。通过对单相电弧炉电极调节系统的仿真结果分析可以看出，该控制方法调节过程较短，超调量较小，抗干扰能力比PID和单纯的反馈线性化控制效果要好。仿真结果对于同类非线性系统的鲁棒控制，具有较强的理论意义和参考价值。
参考文献：
[1] 张向军, 管萍, 刘小河. 电弧炉的间接自适应模糊鲁棒控制[J]. 北京信息科技大学学报, 2009, 24(4): 51-56.
ZHANG Xiang-jun, GUAN Ping, LIU Xiao-he. Indirect adaptive fuzzy robust control of arc furnace[J]. Journal of Beijing Information Science and Technology University, 2009, 24(4): 51-56.
[2] 黄亮， 赵辉. BP网络规则PID在电弧炉电极调节系统中的实现[J]. 天津理工大学学报, 2010, 26(2): 50-53.
HUANG Liang, ZHAO Hui. Implementation of BP network rules PID in electrode regulator system of arc furnace[J]. Journal of Tianjin University of Technology, 2010, 26(2): 50-53.
[3] 王晓亮, 单雪雄.飞艇姿态跟踪系统的研究[J]. 应用数学和力学, 2006, 2(7): 806-811.
WANG Xiao-liang, SHAN Xue-xiong. Study of airship attitude tracking system[J]. Applied Mathematics and Mechanics, 2006, 2(7): 806-811.
[4] LI Lin-lin, YANG Guo-jun, ZHAO Chang-an. Robust controller design for satellite attitude tracking system[J]. Chinese Journal of Aeronautics, 2001, 14(2), 94-99.
[5] 张耀辉, 刘小河. 基于反馈线性化的电弧炉电极调节系统控制[J]. 机床与液压, 2008, 36(7): 264-267.
ZHANG Yao-hui, LIU Xiao-he. Control of regulator system of arc furnace based on feedback linearization[J]. Machine Tool & Hydraulics, 2008, 36(7): 264-267.
[6] Marino R, Tomei P. 非线性系统设计[M]. 姚郁, 贺风华, 译. 北京: 电子工业出版社, 2006: 122-138.
Marino R, Tomei P. Nonlinear control design[M].YAO Yu, HE Feng-hua, transl. Beijing: Publishing House of Electronics Industry, 2006: 122-138.
(编辑 陈爱华)
收稿日期：2011-04-15；修回日期：2011-06-15
基金项目：国家自然科学基金资助项目(51077004)；北京市自然科学基金资助项目(4082010)
通信作者：刘小河(1955-)，男，河南沁阳人，博士，教授，博士生导师，从事非线性系统控制和自适应控制等研究；电话：13910235819；E-mail：liuxiaohe551026@163.com
摘要：讨论电弧炉电极调节系统的反馈线性化鲁棒控制问题。应用微分几何的线性反馈方法对电弧炉电极调节系统的非线性部分进行处理，并在此基础上设计鲁棒控制器，进行MATLAB数字仿真。仿真结果表明，反馈线性化鲁棒控制具有更快的跟踪性能，超调量较小，比PID和单纯的反馈线性化控制效果好。
