J. Cent. South Univ. Technol. (2010) 17: 1264-1270

DOI: 10.1007/s11771-010-0630-1

Forward kinematics analysis of parallel manipulator using modified global Newton-Raphson method

YANG Chi-fu(杨炽夫), ZHENG Shu-tao(郑淑涛), JIN Jun(靳军), ZHU Si-bin(朱思斌), HAN Jun-wei(韩俊伟)

State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150001, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Key words:

parallel manipulator; forward kinematics; global Newton-Raphson; real-time system；

1 Introduction

Parallel manipulator has the advantages of high rigidity, large output force and torque, high accuracy, low moment of inertia and payload capacity, due to the parallel path and averaged link to moving platform error, compared to serial manipulator [1]. It has been extensively studied due to its superior performance and widely applied in various fields such as high fidelity simulators with hydraulic driven system, spacecraft- mounted motion system and spherical radio telescopes [2-3]. For configuration designing, the kinematics is needed to calculate the strokes of actuators and reachable workspace of parallel mechanism. In addition, the singularity of the parallel manipulator cannot be analyzed without kinematics. Furthermore, the forward kinematics in real-time control system is more critical for workspace control scheme. Hence, forward kinematics analysis with an efficient and real time method is very significant for design, control, singularity and workspace analysis of parallel manipulator.

Kinematics of parallel manipulator can be largely divided into two categories, inverse kinematics and forward kinematics [4]. The inverse kinematics is easily realized using closed-form solution [5]. However, the forward kinematics is very complicated for a set of highly nonlinear equations [6]. Recently, most researchers have investigated the forward position problem, and several methods have been proposed [7-9]. Since the number of real solutions is not known, many of these studies are established on the basis of a simplified structure to reduce the nonlinearity of the loop closure equations, such that an analytical approach can be performed to obtain the complete solution set [10]. However, due to manufacturing errors and technology limitations, the simplified or idealized structures may be practically infeasible. There also exist numerical methods that can be used to compute all of the forward position solutions of mechanism that have a more general configuration. These methods rely on the numerical continuation method or exhaustive mono- dimensional search algorithms to solve the polynomial form of the loop closure equations [11-12]. However, the polynomial equations have to be derived separately for different types of parallel manipulators, and the involved computations of these methods are very elaborate. DIDRIT et al [13] presented an approach for obtaining all real forward position solutions of general parallel manipulators using interval analysis, which does not require the polynomial loop closure equations. MERLET [14] used interval analysis to solve forward position problems in parallel manipulators. Yet, these methods are based on interval analysis and the Hansen’s algorithms to search a bounded domain of the moving platform require a considerable amount of computation time. JI and WU [15] showed a concise closed-form solution to the forward kinematics of 6-6p Stewart platform. However, the closed-form solution and its derivations are arduous and time-consuming for real-time system, whose period needs to be 2 ms.

Focusing on different methods for solving the finite displacement problem, it should be noted that they are faced with a great challenge when considering their capacity of generality, automation and efficiency. In view of its simplicity and fast convergence rate, a numerical approach based on the differential loop closure equations and the Newton-Raphson (NR) iterative algorithms, developed earlier for the displacement analysis of multi- loop spatial mechanisms [16], provides an attractive alternative. This method and its variants have been fully studied [17]. Highlighting its quadratic convergence in the solution neighborhood as the main advantage, the estimation methodologies are often used in practice, but not widely applied to the 6-DOF parallel robots. Unfortunately, the numerical stability of this method is highly dependent on the accuracy of the initial approximation of the solution vector. Besides, the NR algorithms can converge only to the particular solution that is closest to the initial approximation. PARIKH and LAM [18] proposed a hybrid strategy where a neural network achieves the starting approximation for the Newton algorithm. The main drawback is that the training, testing and validation for each specific platform demand enormous information from the workspace of each specific mechanism. The use of redundant sensors is another alternative [19]. Sensor measurements in the equation system considerably reduce calculation time and enable correlation of solution to search the corresponding real movement. The disadvantages are that the economic cost is high and the robot sensor system is complex, and the fact is that the number and location of the redundant sensors must be carefully chosen to define a single solution. In addition, the measurement noise and round-off errors should also be reduced.

The traditional NR algorithms for forward kinematics of parallel robots may diverge far away from a root under the initial guesses, even in the nonsingular workspace. For raveling out the problem, a monotonic operator automatically chosen via computer with constraint condition was brought into NR algorithms. The highly nonlinear equations of relationship between actuator positions and generalized spatial pose were gained using geometrical method for 6-DOF parallel robots. By Taylor expansion and Newton type iteration, the MGNR algorithm was developed to solve the nonlinear equations, with a view of estimating the effective direct solution of 6-DOF parallel robots for any initial guesses in the nonsingular workspace without divergence.

2 Kinematics description

The 6-DOF parallel manipulator is composed of a fixed base (down platform) and a moving platform (upper platform) with six actuators supporting it, all actuators are connected with a moving platform and a base with Hooke joints, as shown in Fig.1.

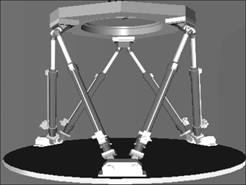
Fig.1 Configuration of 6-DOF parallel manipulator

Fig.2 depicts the definition of coordinate systems, where l_i (i=1, 2, …, 6) represents the length of the ith actuator. The B coordinate system is the body coordinate system fixed to the moving platform, origin O_B of B is the geometry center of the moving platform, axis X_B is the symmetrical line of upper gimbal long spacing of the upper platform, while the L coordinate system is the base coordinate system for the inertial frame. The linear motion denoted as surge (q₁), sway (q₂) and heave (q₃) move along X_L, Y_L and Z_L axes of base coordinate system, respectively, and the angular motion are labeled as roll (q₄), pitch (q₅) and yaw (q₆), which are

Fig.2 Definition of Cartesian system for parallel manipulator

Euler angles of platform on X_B, Y_B and Z_B axes, respectively. The body coordinate system B and the base coordinate system L are superposition in the initial state q_i=0.

The forward kinematics function of the 6-DOF parallel manipulator may be described as:

            (1)

where  represents generalized spatial displacement (position and orientation); and x_i (i=1, …, 6) represents the position of the ith actuator.

3 Forward kinematics under MGNR

Define that c is position vector, c=[q₁, q₂, q₃]^T, and β is rotation Euler angle vector, β=[q₄, q₅, q₆]^T. The upper platform rotates around X-Y-Z under Z-Y-X order.

The position vector c can be projected to the base coordinate system via rotation matrix R parameterized using Euler angles:

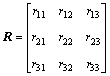                           (2)

where r_ij (i, j=1, 2, 3) is the element of rotation matrix R.

r₁₁=cos q₅ cos q₆;  

r₁₂=cos q₆ sin q₅ sin q₄-sin q₆ cos q₄;

r₁₃=sin q₆ sin q₄+cos q₆ sin q₅ cos q₄;

r₂₁=sin q₆ cos q₅;               

r₂₂=cos q₆ cos q₄-sin q₆ sin q₅ sin q₄;

r₂₃=sin q₆ sin q₅ cos q₄-cos q₆ sin q₄;   

r₃₁=-sin q₅;        

r₃₂=cos q₅ sin q₄;  

r₃₃=cos q₅ cos q₄. 

Therefore, upper gimbal coordinate vector a_i (i= 1, …, 6) in body coordinate system B are transformed to base coordinate system L with projection method.

                                (3)

where (i=1, 2, …, 6) represents upper gimbal coordinate rector in base coordinate system B.

Coordinate vector a_i in body coordinate system and b_i in base coordinate system are constant for the 6-DOF parallel manipulator. The length of actuators may be calculated by

i=1, 2, …, 6         (4)

The displacement of the ith actuator (x_i) is expressed as

x_i=l_i-l₀                                      (5)

where l₀ represents the initial length of actuators at the initial pose [0 0 0 0 0 0]^T. It should be noted that the initial length of each actuator is identical.

Define that x_m is the actual position vector measured by position sensors embedded in actuators. Combining Eqs.(3)-(4) with Eq.(5), there is

                         (6)

where x(Θ) represents the calculated position vector of legs at the pose Θ. Eq.(6) is expanded at the initial  value  in terms of the first-order Taylor series expansion.

                (7)

where  represents the partial derivation of the function  at  The matrix form of Eq.(7) is shown as

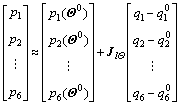                (8)

where q_i⁰ (i=1, 2, …, 6) represents the element of the initial value  represents the Jacobian matrix and can be rewritten as

                        (9)

where H represents transformation matrix between angular velocity in {L} and derivation of Euler angle β; A represents coordinate matrix of upper gimbal, A=[a₁, …, a₆]; l′ represents normalized length matrix of actuators, l′=[l₁, l₂, …, l₆]; l_i′ and H are given as follows:

 i=1, 2, …, 6         (10)

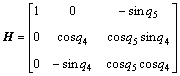               (11)

The Jacobian matrix is allowed to be singular in general parallel robots. Yet, the parallel manipulator is mechanically designed to avoid such a singularity in the workspace, only a generalized displacement can be solved in the workspace for a set of actuator lengths under the MGNR algorithm.

Making use of the modified global NR algorithm, the real-time solution of system states of the parallel manipulator may be computed for the input of actual actuator length with the following equation:

 (0＜λ＜1)      (12)

where x_j-1 represents the calculated actuator length related to  via Eqs.(3)-(5), and j represents iteration number, j=1, 2, …, n.

The MGNR algorithm automatically selects a value of descent operator which satisfies the following equations during iteration for Eq.(12):

＜                       (13)

                                   (14)

where D is workspace of the parallel manipulator.

For the case that Eqs.(13)-(14) are true with the value λ₀=0.6 (0.6 is chosen for λ in the first iteration), otherwise, λ=λ₀^k, which satisfies that Eqs.(13)-(14) are true after k times justification during the jth iteration under MGNR, is selected as the value of descent operator. With respect to iteration, the value of operator λ is automatically selected in terms of the above process via program.

The termination condition, which is also the objective function of the MGNR algorithm, is given as

＜ε                   (15)

j≤n                                      (16)

where ε is a infinite decimal; and n is the maximal number of iteration.

4 Results and discussion

In order to clarify and verify the performance (accuracy, real time and convergence) of the modified global Newton-Raphson algorithm for 6-DOF parallel manipulator, a specified 6-DOF parallel manipulator was utilized to evaluate the MGNR algorithm. The initial generalized displacement is zero, and six identical actuators are of the same length with zero positions in initial state. With configuration parameters available, the actuator positions can be calculated with known generalized displacement of moving platform under closed-form solution, and the generalized spatial states of moving platform of the 6-DOF parallel manipulator may be estimated by the algorithm proposed in this work under actual actuator positions measured by position sensors. The joint coordinate matrices A and B of the 6-DOF parallel manipulator are shown as (unit is m):

(17)

(18)

The initial length of actuators l₀ is 3.05 m, while the generalized coordinate  should be zero for a set of zero actuator displacements. Applying the proposed algorithm to a real-time industrial computer, the spatial states of the 6-DOF parallel manipulator was computed by Eq.(12) with actuator position x_m=0, the termination condition of the MGNR algorithm was set as ε=1×10^-9 and n=4. The sample time of the real time system was fixed to 2 ms. The solution of the MGNR algorithm is given  as

[1.7×10^-16, 1.1×10^-16, -1.5×10^-16, 0.5×10^-16,

 0.05×10^-16, 1.0×10^-16]^T                  (19)

The maximal linear error is 1.7×10^{-16 m in linear motion, 1}×10^-16 rad in angular motion for this computation, which can be neglected considering the fact that the maximal error is much smaller than the generalized precision requirement. Hence, the MGNR algorithm can be used to solve 6-DOF displacements with ignored errors for 6-DOF parallel manipulator. With a view of better confirming the accuracy of the presented algorithm, a generalized coordinate  that was far away from the initial state was given to the manipulator, =[c  β]^T, c=[0.1  0.2  0.3]^T m, β=[0.02  0  0]^T rad. The position of actuators (x₁) can be calculated by Eqs.(4)-(5) with closed-form solutions with regard to the desired coordinate

x₁=[-0.092 9, -0.233 9, -0.250 8, -0.119 8, -0.348 4,

-0.336 6]^T                               (20)

Based on the MGNR algorithm, the generalized coordinate  related to the position of actuators x₁ was solved, which is shown as follows

[0.1, 0.2, 0.3, 0.02, -1.2×10^-16, -0.8×10^-16]^T (21)

The maximal error is 9×10^{-15 m in surge, -1.2}× 10^-16 rad in roll for the desired generalized coordinate. In order to confirm the accuracy of the MGNR algorithm, five different generalized coordinates of the parallel robots were assumed to be the real pose of platform, and the direct solutions relative to the actuator displacements with respect to real poses were solved with the MGNR algorithm. The real and estimated poses of the parallel robots are shown in Table 1.

From Table 1, it can be seen that the maximal absolute error is 2.09×10^{-10 m in yaw, 2.05}×10^-11 rad in roll for the five estimated generalized poses with the MGNR algorithm. Consequently, the accuracy of the MGNR algorithm for the 6-DOF parallel manipulator can be higher than the termination condition 1×10^{-9 m in linear motion and 1}×10^-9 rad in angular motion. It should be noted that the precision can far satisfy the requirements for such a long stroke 6-DOF parallel manipulator in practice.

The parallel robots always alter its generalized spatial pose continuously during movement. On the assumption that the actual trajectory of the moving platform of the parallel robots is a random signal in surge, the actual actuator displacements of the parallel robots were solved using analytical method concerning the real trajectory, and then the estimated trajectory was computed with the actual actuator displacements as inputs by using MGNR algorithm. The estimated generalized pose of the 6-DOF parallel robots compared with the real pose is depicted in Figs.3-4, and the maximal errors of the forward kinematics under specified linear and angular motion with the MGNR algorithm in all DOFs are shown in Figs.5-6.

Table 1 Real and estimated generalized poses of parallel robots

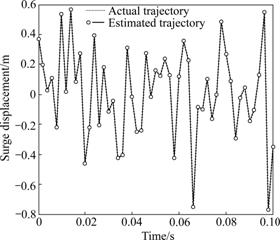
Fig.3 Comparison of actual and estimated trajectories in surge

Comparison between the actual pose and estimated pose indicates that the trajectories of parallel manipulator achieved by the proposed MGNR algorithm are fully consistent with the real trajectories, and the maximal error is -9.967×10^{-10 m in linear motion, and 4.936}×10^-10 rad in angular motion for dynamic motion. The estimated errors of the MGNR algorithm for the 6-DOF parallel robots are less than 1×10^{-9 m and 1}×10^-9 rad for the random motion. Hence, for both constant and dynamic movements, the forward kinematics with the MGNR algorithm can solve direct solution of 6-DOF parallel robots with high accuracy, which is much higher than the set precision of algorithm (1×10^-9 m in linear motion and 1×10^-9 rad in angular motion).

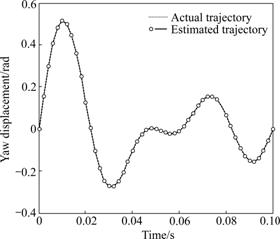
Fig.4 Comparison of actual and estimated trajectories in yaw

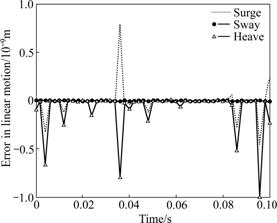
Fig.5 Errors in linear motion of forward kinematics

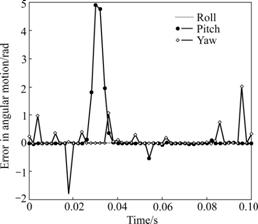
Fig.6 Errors in angular motion of forward kinematics

To confirm the performances of MGNR algorithm in practice, an actual 6-DOF parallel manipulator is given in Fig.7. The sampling time is set to 1 ms for the experimental system.

Fig.7 Experimental 6-DOF parallel manipulator

Under consideration, only the actuator positions can be measured by position sensors simultaneously during motion. The performance of the presented algorithm for forward kinematics of 6-DOF parallel manipulator may be evaluated through comparing the measured actuator positions with those calculated with the estimated pose of MGNR, which can be also referred in Ref.[20]. A pitch motion (1(?)/2 Hz) is applied to the platform, the computed and measured actuator positions are shown in Fig.8. The errors between measured and estimated leg positions are depicted in Fig.9.

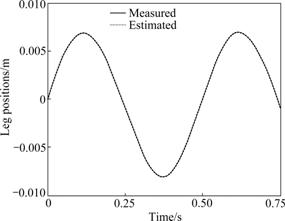
Fig.8 Comparison of estimated and measured leg positions

The dot line is the estimated leg positions, and the solid line is measured leg positions by position sensors embedded in actuators in Fig.8. As can be seen from Fig.8 and Fig.9, the estimated actuator positions are consistent with measured actuator positions; the maximal error between estimated and measured positions is less than 1×10^{-9 m. Hence, the proposed algorithm for forward kinematics can solve the generalized pose of moving platform with high accuracy, which can be applied to actual 6-DOF parallel manipulator.}

Besides the accuracy of the proposed algorithm, the executed time and convergence of the MGNR algorithm were also tested via experiment. In practical real-time control system, the property of real time of the algorithm is very important for closed loop control scheme. The MGNR algorithm was executed in MATLAB/RTW/xPC, which was a real-time operation system, and the executed computer was an industrial control computer with Advantech Pentium IV2.4G and on-time RT-OS32 real time kernel. The maximal iteration number of the algorithm was set to five, and precision of iteration was  1×10^{-9 m}. The executed time of MGNR algorithm and Newton-Raphson algorithm are shown in Table 2.

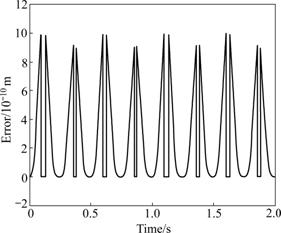
Fig.9 Errors between estimated and measured leg positions

Table 2 Executed time of algorithm in real-time systems

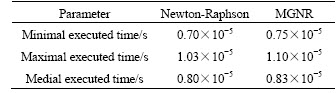
The initial guesses for both NR and MGNR algorithms are zero. The medial executed time of the MGNR algorithm is 0.83×10^-5 s, which is 0.03×10^-5 s longer than that of Newton-Raphson algorithm. Although the medial computed time of the MGNR algorithm is longer than that of NR, the property of real time of MGNR and Newton-Raphson is not distinct for either 1 or 2 ms real-time system. The evaluation for computed time of the NR and MGNR algorithms is under the same initial guess that two algorithms can converge to the real solution. However, if the initial guess value is selected away from the root, the NR algorithm may be divergent during iteration, which is more dangerous for the system involved the generalized displacements as feedback. Fortunately, the presented MGNR algorithm can converge to the real solutions regardless of the initial guess value included in the workspace. An initial guess value far away from the root of forward kinematics was chosen for both NR and MGNR algorithms in the workspace of the parallel manipulator. The convergence characteristics are shown in Fig.10.

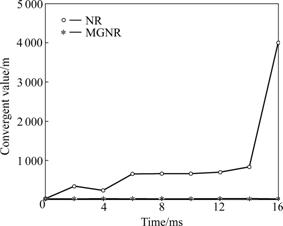
Fig.10 Curves of convergence for NR and MGNR algorithms

As shown in Fig.10, the NR algorithm diverges under the initial guesses far away from the real solution after one time iteration, and the trend for solution of NR algorithm is quickly kept away from the effective root. While the MGNR algorithm converges to the optimal solution after one times iteration. Therefore, the proposed MGNR algorithm can be used to deal with the forward kinematics problem even the initial guess value is chosen far away from the root of 6-DOF parallel manipulator.

5 Conclusions

(1) The MGNR algorithm is developed, and the proposed algorithm can solve the actual solution of direct kinematics problem for 6-DOF parallel manipulator without divergence even if the initial guess value is chosen far away from the root.

(2) The forward kinematics is defined to solve the position and orientation of moving platform with a set of given positions of actuators for 6-DOF parallel manipulator, and the highly nonlinear equations of the forward kinematics are derived based on geometrics.

(3) The accuracy, effectiveness and convergence of the proposed algorithm are confirmed in a real time system for a specified 6-DOF parallel manipulator; and the algorithm can estimate and converge to the real solution of the forward kinematics in real time, which is much less than 1 ms.

References

[1] MERLET J P. Parallel manipulator [M]. Norwell, MA: Kluwer Academic Publishers, 2000: 6-12.

[2] CHIN J H, SUN Y H, CHENG Y M. Force computation and continuous path tracking for hydraulic parallel manipulators [J]. Control Engineering Practice, 2008, 16(6): 697- 709.

[3] HE Qing-hua, HE Xiang-yu, ZHU Jian-xin. Fault detection of excavator’s hydraulic system based on dynamic principal component analysis [J]. Journal of Central South University of Technology, 2008, 15(5): 700-705.

[4] Bande P, Seibt M, Uhlmann E, SAHA S K, RAO P V M. Kinematics analysis of Dodekapod [J]. Mechanism and Machine Theory, 2005, 40(6): 740-756.

[5] Jaime G A, Jose M R M, Gursel A. Kinematics and singularity analyses of a 4-DOF parallel manipulator using screw theory [J]. Mechanism and Machine Theory, 2006, 41(9): 1048-1061.

[6] PETUYA V, GUTIERREZ J M, ALONSO A, ALTUZARRA O, HERNANDEZ A. A numerical procedure to solve non-linear kinematic problems in spatial mechanism [J]. International Journal for Numerical Methods in Engineering, 2008, 73(6): 825-843.

[7] JIN Y, CHEN I M, YANG G L. Kinematic design of a 6-DOF parallel manipulator with decoupled translation and rotation [J]. IEEE Transactions on Robotics, 2006, 22(3): 545-551.

[8] BARON L, ANGELES J. The direct kinematics of parallel manipulator under join-sensor redundancy [J]. IEEE Transactions on Robotics and Automation, 2000, 16(1): 12-19.

[9] LEE T Y, SHIM J K. Improved dialytic elimination algorithms for the forward kinematics of the general Stewart-Gough platform [J]. Mechanism and Machine Theory, 2003, 38(6): 563-577.

[10] SELFRIDGE R G, MATTHEW G K. Forward analysis of some special Stewart platforms [J]. Journal of Robotic System, 2000, 17(10): 517-526.

[11] RAGHAVAN M. The Stewart platform of general geometry has 40 configurations [J]. ASME Journal of Mechanical Design, 1993, 115(2): 227-282.

[12] KAMRA R, KOHLI D, DHINGRA A K. Forward displacement analysis of a six-DOF parallel manipulator actuated by 3R3P and 4R2P chains [J]. Mechanism and Machine Theory, 2002, 37(6): 619- 637.

[13] DIDRIT O, PETITOT M, WALTER E. Guaranteed solution of direct kinematic problems for general configuration of parallel manipulator [J]. IEEE Transactions on Robotics and Automation, 1998, 14(2): 259-265.

[14] MERLET J P. Solving the forward kinematics of a Gough-type parallel manipulator with interval analysis [J]. International Journal of Robotics Research, 2004, 23(3): 221-235.

[15] JI Ping, WU Hong-tao. A closed-form forward kinematics solution for the 6-6P Stewart platform [J]. IEEE Transactions on Robotics and Automation, 2001, 17(4): 522-526.

[16] Quarteroni A, Sacco R, Saleri F. Numerical mathematics [M]. Berlin: Springer, 2000: 80-87.

[17] KELLEY C T. Solving nonlinear equations with Newton’s method [M]. Philadelphia: SIAM, 2003: 158-165.

[18] PARIKH P J, LAM S S Y. A hybrid strategy to solve the forward kinematics problem in parallel manipulators [J]. IEEE Transactions on Robotics, 2005, 21(1): 18-25.

[19] Rocco V, Vincenzo P C. Accurate and fast body pose estimation by three point position data [J]. Mechanism and Machine Theory, 2007, 42(9): 1170-1183.

[20] KIM H S, CHO Y M, LEE K. Robust nonlinear task space control for 6 DOF parallel manipulator [J]. Automatic, 2005, 41(9): 1591-1600.

(Edited by LIU Hua-sen)