文章编号:1004-0609(2013)08-2104-06
7055铝合金加筋板蠕变时效成形有限元仿真
湛利华1,许晓龙2,贾树峰2,阳 凌2
(1. 中南大学 机电工程学院,长沙 410083;
2. 中南大学 高性能复杂制造国家重点实验室,长沙 410083)
摘 要:
基于铝合金时效成形机理的蠕变统一本构方程,应用大型商业化有限元软件MSC.Marc,对其进行二次开发,实现7055铝合金加筋板蠕变时效成形过程仿真模拟,结合ATOS Professional软件分析加筋板成形后回弹率,并通过实验研究验证仿真结果的正确性。结果表明:单纯静力加载后加筋板的回弹量为16.14%,而经过蠕变时效后加筋板的回弹量降低为10.34%,筋条对构件蒙皮的回弹起到一定的抑制作用;蠕变时效后加筋板的几何形状是由筋板的塑性变形与构件的蠕变应变共同决定的。
关键词:
中图分类号:TG146.21 文献标志码:A
Finite element simulation for creep age forming of 7055 aluminum alloy stiffened panel
ZHAN Li-hua1, XU Xiao-long2, JIA Shu-feng2, YANG Ling2
(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
2. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)
Abstract: The creep unified constitutive equations based on aluminum alloy aging forming mechanism were further developed by the large scale commercial finite element software MSC.Marc, and 7055 aluminum alloy stiffened panel creep age forming process simulations were completely conducted. Then springback of the stiffened plate after forming was calculated by ATOS Professional software, and its correctness was verified by experimental studies. The results show that, the springback of the stiffened plate under the simple static load is 16.14%, while it reduces to 10.34% after creep age forming, which shows that ribs play some certain role on the springback of the skin in the process of creep age forming. And the geometry shape of the stiffened plate after creep age forming is jointly determined by the plastic deformation of the ribs and the creep strain of the workpiece.
Key words: aluminum alloy 7055; creep age forming; finite element simulation; springback
在20世纪80年代初,为了解决整体壁板的成形难题而开发了的一项利用金属的蠕变特性、将成形与时效同步进行的成形方法[1-2],即蠕变时效成形技术。目前,该技术在国外得到深入研究并已应用于实际生产中[3-7],如美国B-1B超音速战略轰炸机上下机翼壁板等;而在国内由于缺乏必要的基础研究和技术储备,该技术尚未得到工程化应用。
已有研究[8-11]表明,经过蠕变时效成形后的工件,卸载后均存在一定的回弹量,在一定条件下其回弹量甚至高达70%,这严重影响工件的成形精度。对此国内外学者开展了一系列工作,研究蠕变时效对铝合金材料成形成性的影响,HO等[8]研究了760 mm×760 mm尺寸板件在不同厚度下的回弹行为,得到板件成形后回弹率随着壁板厚度增加而减小的规律;李超等[9]研究了7B04铝合金在不同时效条件下的蠕变行为,分析了加工条件对材料微观组织与力学性能的影响;HO等[10]研究了工件在发生单、双曲率弯曲时的蠕变时效成形行为,发现相同工况下工件在双曲率弯曲时发生的回弹比单曲率要小等。然而这些研究工作的对象绝大部分为铝合金蒙皮,目前仅个别学者对带筋工件进行了蠕变时效行为研究[12-17]。甘忠等[15]和黄霖等[16-17]研究不同铝合金材料整体壁板回弹变化,但均未对筋条在蠕变时效成形过程中对回弹的影响展开研究,其研究成果不能有效指导复杂构件的实际成形。
使用Fortran语言通过二次开发,将7055铝合金蠕变时效统一本构方程嵌入到有限元软件MSC.MARC中,对带筋铝合金壁板蠕变时效成形过程进行数值模拟,结合ATOS Professional软件分析工件回弹,并开展相应工况下加筋板蠕变时效成形实验研究,验证仿真模型的准确性。
1 蠕变时效统一本构方程
选取7055铝合金材料进行等温蠕变时效实验,实验温度为120 ℃,时效时间为24 h,得到190.0、252.2、308.9、357.8 MPa 4种恒应力作用下的蠕变曲线;并通过宏观性能及微观组织分析,分别获得不同时效条件下7055铝合金屈服强度及析出相尺寸的大小。参考文献[8]对铝合金板材蠕变时效成形本构方程的研究,结合时效析出硬化、位错硬化、固溶强化、位错密度和析出相半径等因素在蠕变时效中的演变机制,建立一套完整的7055铝合金蠕变时效统一本构方程[18],具体方程如下:
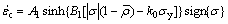 (1)
(1)
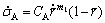 (2)
(2)
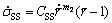 (3)
(3)
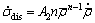 (4)
(4)
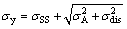 (5)
(5)
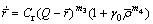 (6)
(6)
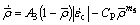 (7)
(7)
式中: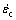 为蠕变应变率;
为蠕变应变率;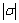 为时效应力绝对值;
为时效应力绝对值;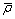 为归一化位错密度;
为归一化位错密度; 为时效硬化强度变化率;
为时效硬化强度变化率;  为固溶强化强度变化率;
为固溶强化强度变化率;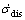 为位错硬化强度变化率;
为位错硬化强度变化率;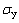 为材料屈服强度;
为材料屈服强度;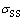 为固溶强化强度;
为固溶强化强度;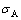 为时效硬化强度;
为时效硬化强度;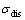 为位错硬化强度;
为位错硬化强度; 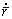 为归一化析出相半径变化率;
为归一化析出相半径变化率;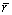 为归一化析出相半径;
为归一化析出相半径; 为归一化位错密度变化率;A1、B1、k0、CA、m1、CSS、m2、n、A2、Cr、Q、
为归一化位错密度变化率;A1、B1、k0、CA、m1、CSS、m2、n、A2、Cr、Q、 、m3、m4、A3、CP和m5为材料常数。
、m3、m4、A3、CP和m5为材料常数。
将实验得到的蠕变曲线、屈服强度及析出相半径与理论计算曲线作比较,并以其差值作为目标函数进行优化处理,具体分析见参考文献[18],得到本构方程中材料常数值,如表1所列。本构方程与实验数据的拟合情况见图1。
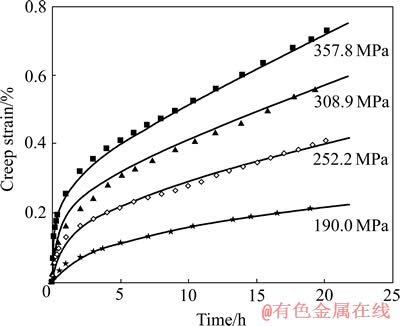
图1 7055铝合金蠕变时效实验数据与拟合曲线
Fig. 1 Creep age test data and fitting curves of 7055 aluminum alloy
表1 120 ℃下7055铝合金蠕变时效本构方程材料常数值
Table 1 Determined constants in creep age forming constitutive equations for 7055 aluminum alloy at 120 ℃

2 蠕变时效有限元仿真
2.1 有限元模型建立
研究对象加筋工件采用7055铝合金材料,其几何尺寸如图2所示。工件的长宽规格为281 mm×272 mm,其中横向(即弯曲方向)上的筋条厚度为4 mm,纵向筋条厚度为2 mm,所有筋条高度为18 mm,工件的蒙皮厚度为2 mm。

图2 7055铝合金加筋板的几何尺寸
Fig. 2 Geometry of 7055 aluminum alloy stiffened panel (Unit: mm)
根据蠕变时效成形工艺,对加筋板进行单曲率弯曲时效成形,建立相应的有限元模型,如图3所示。其中,成形模具型面为曲率半径R0 =1 m的钢材圆柱面(即工件成型的目标曲面),其厚度为12 mm。工件与模具型面之间使用4个可支撑工件质量的弹簧连接。采用3D壳单元对壁板工件与模具型面划分网格,同时为保证计算精度,将壁板工件沿厚度方向剖分为5层单元。
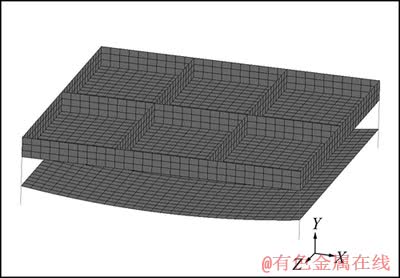
图3 7055铝合金加筋板有限元分析模型
Fig. 3 Finite element analysis model of 7055 aluminum alloy stiffened panel
2.2 蠕变时效有限元分析过程
为了探究筋条在蠕变时效前后对工件成形回弹的影响,开展如下对比研究。
首先,进行常温下单纯静力加载时的仿真计算,此时并没有考虑蠕变时效过程。具体的有限元分析步骤如下:
(1) 在壁板工件上施加适当的均布载荷,使弹簧压缩且工件的4个角与模具型面相接触;
(2) 继续在工件上施压,使其发生形变并与模具型面完全紧密接触;
(3) 常温环境中保持载荷和工件变形5 min后卸载。
其次,进行加筋板的蠕变时效成形仿真计算。使用Fortran语言编写用户子程序CREEP,将7055铝合金蠕变时效统一本构方程嵌入到MSC.Marc中进行有限元分析。根据蠕变时效成形工艺过程,结合有限元模型,建立以下分析步骤:
(1)、(2)步骤与常温静力加载仿真步骤相同;
(3) 将工件加热至120 ℃,保持热力载荷和壁板工件变形24 h。在恒定时效温度(120 ℃)下,工件发生蠕变和应力松弛,部分弹性变形转变为塑性变形,材料内部应力水平下降;
(4) 卸载,工件自然回弹。
2.3 有限元仿真结果
分别对加筋板的常温静力加载与蠕变时效的仿真结果进行研究,分析两种工况下加筋板的成形情况与回弹大小。
2.3.1 常温静力加载的结果分析
分析静力加载仿真结果发现,静力加载完毕时加筋板的最大等效应力为428.5 MPa,卸载后加筋板的最大等效应力为342.4 MPa,如图4所示。同时分析卸载后加筋板等效塑性应变云图(图5)发现,加筋板的筋条沿曲率方向发生了一定的塑性变形,但是加筋板的蒙皮部分仍然处于弹性变形阶段。
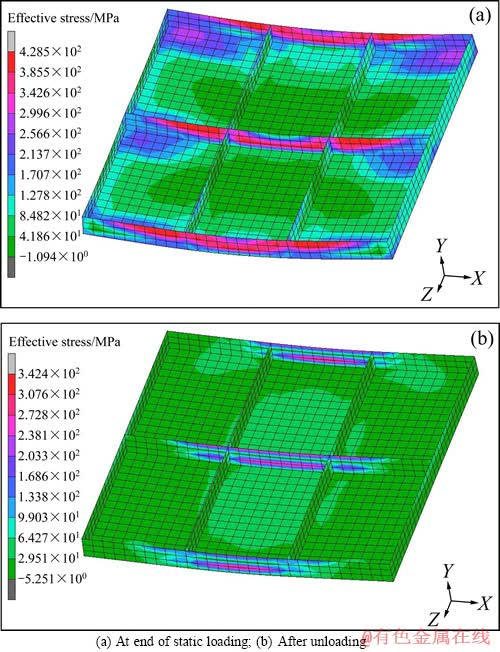
图4 静力加载过程中7055铝合金加筋板的等效应力
Fig. 4 Equivalent stress of 7055 aluminum alloy stiffened panel in static loading process

图5 静力加载后7055铝合金加筋板等效塑性应变
Fig. 5 Equivalent plastic strain of 7055 aluminum alloy stiffened panel after static loading
将卸载后的加筋板蒙皮网格文件导入ATOS Professional软件中进行截面圆拟合处理,分析测得经过静力加载后,工件蒙皮的曲率半径Rf为1 182.07 mm。根据回弹公式SP=(Rf-R0)/Rf (其中,SP为工件回弹率,Rf为工件回弹后曲率半径,R0为模具型面曲率半径)计算得到,工件经过常温静力加载后的回弹为16.14%,可以看出加筋板发生的回弹比较少。分析发现,这主要是由于加筋板的筋条在静力加载阶段即发生了塑性变形,一定程度上抑制了工件蒙皮的回弹,这对后续研究工件蠕变时效成形的回弹特征至关重要。
2.3.2 蠕变时效的结果分析
图6所示为7055铝合金加筋板蠕变时效成形后的等效应力云图。由图6可得,加载完毕时(蠕变时效开始前)加筋板的最大等效应力为482.5 MPa,随着蠕变时效的进行,发生应力松弛现象,时效结束时,加筋板的最大等效应力减小到260.1 MPa,而在卸载后,加筋板的最大等效应力为178.4 MPa。同样分析加筋板等效塑性应变云图(如图7所示)发现在卸载后,加筋板的筋条发生了一定的塑性变形,而加筋板的蒙皮仍然处于弹性变形阶段。
同样使用ATOS Professional软件分析蠕变时效后的加筋板蒙皮,分析测得经过蠕变时效后,工件蒙皮的曲率半径Rf为1 115.36 mm。根据回弹公式SP=(Rf-R0)/Rf计算可以得到,工件的回弹为10.34%。因此可以得到加筋板在经过蠕变时效后,发生的回弹小于静力加载后的结果,两者相差5.8%。首先,静力加载结束后,加筋板筋条发生的塑性变形,在一定程度上抑制了工件蒙皮的回弹;其次,随着蠕变时效的进行,工件一部分的弹性变形转变为塑性变形,进一步抑制了回弹的发生。最终,加筋板工件会发生更小的回弹。
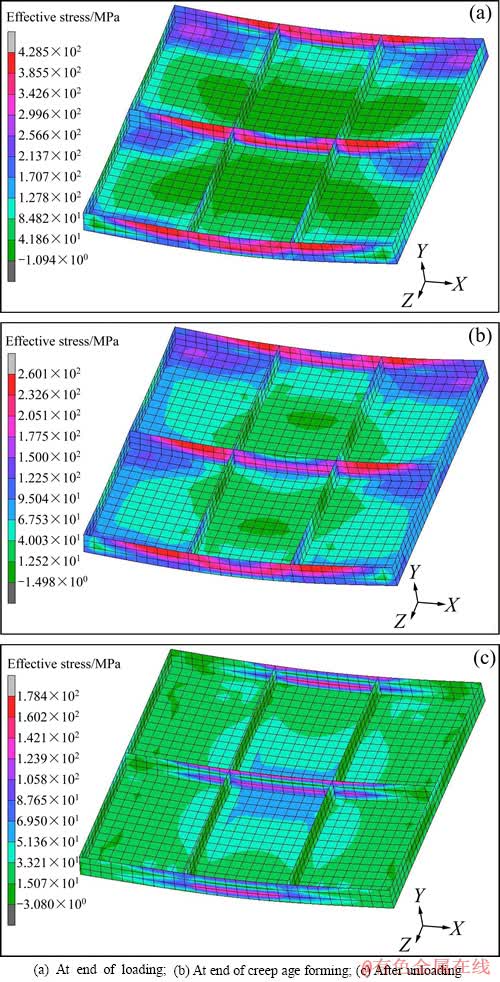
图6 蠕变时效过程中7055铝合金加筋板等效应力
Fig. 6 Equivalent stress of 7055 aluminum alloy stiffened panel in creep age forming process

图7 蠕变时效后7055铝合金加筋板等效塑性应变
Fig. 7 Equivalent plastic strain of 7055 aluminum alloy stiffened panel after creep age forming
3 实验研究
为了验证有限元仿真结果的准确性,进行与有限元模拟相同工艺条件下的实验研究。蠕变时效实验工装采用筋板类模具,如图8所示,其中筋板模面曲率半径为1 m,通过调节模具上端的螺钉高度进行加载。为了避免在加载过程中螺钉的冲挤造成构件筋条的人为变形,加载前,在加筋板与螺钉之间添加一块薄钢板保护构件筋条。

图8 蠕变时效成形实验工装
Fig.8 Experiment tooling of creep age forming
首先,进行常温静力加载实验。调节螺钉高度对构件施加载荷,并保证构件蒙皮与下模紧密接触;保持构件几何变形5 min后卸载;其次,进行高温蠕变时效实验。首先,对构件加载并保证其与下模紧密贴合;然后将模具与构件放入时效炉中进行高温处理,设定构件的时效温度为120 ℃,时效总时间为24 min;最后,结束高温,打开炉门,在构件空冷结束后卸载螺钉加载,使构件回弹。图9所示为蠕变时效试验结束后的加筋工件。在实验结束后,采用ATOS COMPACT SCAN设备对试验件蒙皮表面进行扫描,得到加筋板蒙皮的三维网格数据,并导入ATOS Professional软件中处理得到加筋板蒙皮试验后的曲率半径值。

图9 蠕变时效后工件
Fig. 9 Workpiece after creep aging forming
通过ATOS Professional软件分析得到,经过静力加载试验后,加筋板蒙皮的曲率半径为1 215.25 mm,而有限元仿真得到的蒙皮曲率半径为1 182.07 mm,计算得到两者的相对误差为2.73%;同时经过蠕变时效试验后,加筋板蒙皮的曲率半径为1 124.64 mm,而有限元仿真得到的蒙皮曲率半径为1 115.36 mm,计算得两者的相对误差为0.83%。由此可见,试验和仿真结果之间误差很小,充分证明有限元仿真模型的准确性。
4 结论
1) 给定尺寸的加筋板在进行单纯静力加载后,仅是构件筋条部分发生了塑性变形,蒙皮仍处于弹性变形状态。筋条的塑性变形在一定程度上抑制了构件的回弹,最终决定其几何形状,卸载后构件的回弹为16.14%。
2) 对加筋板进行蠕变时效处理时,随着蠕变时效的进行,构件部分弹性变形转变为塑性变形,塑性变形量的增加进一步抑制回弹的发生,卸载后,构件发生了10.34%的回弹,回弹量减小。
3) 经过蠕变时效成形,加筋板的几何形状是由初始加载引起的构件塑性变形与后面的蠕变时效两者共同作用的结果。
REFERENCES
[1] MITCHELL C H. Autoclave age forming large aluminum aircraft panels[J]. Journal of Mechanical Working Technology, 1989, 20: 477-488.
[2] DENISE M H. Age forming technology expanded in an autoclave[C]// General Aviation Aircraft Metting and Exposition. Wichita, KS: SAE, 1985: 850-885.
[3] SALLAH M, PEDDIESON J, FOROUNDASTAN S. A mathematical model autoclave age forming[J]. Journal of Materials Processing Technology, 1991, 28(9): 211-219.
[4] LEVER A, PRIOR A. Finite element analysis of shot peening[J]. Journal of Materials Processing Technology, 1998, 80: 304-308.
[5] LIN J, HO K C, DEAN T A. An integrated process for modelling of precipitation hardening and springback in creep age forming[J]. International Journal of Machine Tools and Manufacture, 2006, 46(11): 1266-1270.
[6] JEUNECHAMPSA P P, HO K C, LIN J, PONTHOT J P, DEAN T A. A closed form technique to predict springback in creep age forming[J]. International Journal of Mechanical Sciences, 2006, 48(6): 621-629.
[7] NARIMETL S P, PEDDIESON J JR, BUNCHANAN G R, FOROUNDASTAN S. A simulation procedure for panel age forming[J]. Journal of Engineering Materials and Technology, 1998, 120(2): 183-190.
[8] HO K C, LIN J, DEAN T A. Constitutive modeling of primary creep for age forming an aluminum alloy[J]. Journal of Materials Processing Technology, 2004, 153: 122-127.
[9] 李 超, 万 敏, 黄 霖. 7B04铝合金蠕变过程中析出相的影响因素[J]. 航空材料学报, 2009, 29(2): 13-17.
LI Chao, WAN Min, HUANG Lin. Effect on precipitation phases of 7B04 aluminum alloy during creep process[J]. Journal of Aeronautical Materials, 2009, 29(2): 13-17.
[10] HO K C, LIN J, DEAN T A. Modelling of springback in creep forming thick aluminium sheets[J]. International Journal of Plasticity, 2003, 20(4/5): 733-751.
[11] GAN Zhong, ZHU Jia-zan, ZHANG Lei. Research on springback compensation of mold surface for age forming of integral panel[J]. Journal of Plasticity Engineering, 2010, 17(5): 15-18.
[12] 黎俊初, 邹 唤, 熊洪淼, 谭险峰, 常 春. 筋板类LY12铝合金零件蠕变时效成形有限元分析[J]. 塑性工程学报, 2010, 17(2): 24-27.
LI Jun-chu, ZOU Huan, XIONG Hong-miao, TAN Xian-feng, CHANG Chun. FE analysis on creep age forming of Al alloy LY12 ribbed-plate parts[J]. Journal of Plasticity Engineering, 2010, 17(2): 24-27.
[13] NACEUR H, GUO Y Q, BEN-ELECHI S. Response surface methodology for design of sheet forming parameters to control springback effects[J]. Computers and Structures, 2006, 84(26/27): 1651-1663.
[14] KARAFILLIS A P, BOYCE M C. Tooling design in sheet metal forming using springback calculations[J]. International Journal of Mechanical Sciences, 1992, 34(2): 113-131.
[15] 甘 忠, 张 磊, 许旭东, 袁 胜. 整体壁板时效成形模具回弹补偿的工艺研究[J]. 塑性工程学报, 2010, 17(5): 15-18.
GAN Zhong, ZHANG Lei, XU Xu-dong, YUAN Sheng. Research on springback compensation of mold surface for age forming of integral panel[J]. Journal of Plasticity Engineering, 2010, 17(5): 15-18.
[16] 黄 霖, 万 敏, 吴向东, 迟彩楼, 季秀升, 李善良, 张新娟. 整体壁板时效成形的回弹预测及模面补偿技术[J]. 航空学报, 2009, 30(8): 1531-1536.
HUANG Lin, WAN Min, WU Xiang-dong, CHI Cai-lou, JI Xiu-sheng, LI Shan-liang, ZHANG Xin-juan. Prediction of springback and tool surface modification technology for age forming of integral panel[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(8): 1531-1536.
[17] 黄 霖, 万 敏. 铝合金厚板时效成形回弹补偿算法[J]. 航空学报, 2008, 29(5): 1406-1410.
HUANG Lin, WAN Min. Compensation algorithm for springback in age forming for aluminum alloy plate[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1406-1410.
[18] ZHAN Li-hua, LIN Jian-guo. Experimental studies and constitutive modelling of the hardening of aluminium alloy 7055 under creep age forming conditions[J]. International Journal of Mechanical Sciences, 2011, 53: 595-605.
(编辑 李艳红)
基金项目:国家重点基础研究发展计划资助项目(2010CB731700);国家自然科学基金重点基金项目(51235010)
收稿日期:2012-09-19;修订日期:2013-06-08
通信作者:湛利华,教授,博士;电话:0731-88830254;E-mail: yjs-cast@csu.edu.cn
摘 要:基于铝合金时效成形机理的蠕变统一本构方程,应用大型商业化有限元软件MSC.Marc,对其进行二次开发,实现7055铝合金加筋板蠕变时效成形过程仿真模拟,结合ATOS Professional软件分析加筋板成形后回弹率,并通过实验研究验证仿真结果的正确性。结果表明:单纯静力加载后加筋板的回弹量为16.14%,而经过蠕变时效后加筋板的回弹量降低为10.34%,筋条对构件蒙皮的回弹起到一定的抑制作用;蠕变时效后加筋板的几何形状是由筋板的塑性变形与构件的蠕变应变共同决定的。
[9] 李 超, 万 敏, 黄 霖. 7B04铝合金蠕变过程中析出相的影响因素[J]. 航空材料学报, 2009, 29(2): 13-17.
[12] 黎俊初, 邹 唤, 熊洪淼, 谭险峰, 常 春. 筋板类LY12铝合金零件蠕变时效成形有限元分析[J]. 塑性工程学报, 2010, 17(2): 24-27.
[15] 甘 忠, 张 磊, 许旭东, 袁 胜. 整体壁板时效成形模具回弹补偿的工艺研究[J]. 塑性工程学报, 2010, 17(5): 15-18.
[16] 黄 霖, 万 敏, 吴向东, 迟彩楼, 季秀升, 李善良, 张新娟. 整体壁板时效成形的回弹预测及模面补偿技术[J]. 航空学报, 2009, 30(8): 1531-1536.
[17] 黄 霖, 万 敏. 铝合金厚板时效成形回弹补偿算法[J]. 航空学报, 2008, 29(5): 1406-1410.


