- Abstract:
- 1 Introduction▲
- 2 Governing equation...▲
- 3 Formulation of pro...▲
- 4 Boundary condition...▲
- 5 Case study▲
- 6 Conclusions▲
- References
- Figure
- Fig. 1 Concentrated source acting on saturated porous media with incompressible fluidhalf space (a) and source over circular region acting on saturated porous media with incompressible fluid half space (b)
- Fig. 2 Variation of normal stress σzz with distance r due to concentrated normal force
- Fig. 3 Variation of normal stress σzz with distance r due to concentrated tangential force
- Fig. 4 Variation of normal stress σzz with distance r due to concentrated pressure source
- Fig. 5 Variation of pore pressure p with distance r due to concentrated normal force
- Fig. 6 Variation of pore pressure p with distance r due to concentrated tangential force
- Fig. 7 Variation of pore pressure p with distance r due to concentrated pressure source
- Fig. 8 Variation of tangential stress σzr with distance r due to concentrated normal force
- Fig. 9 Variation of tangential stress σzr with distance r due to concentrated tangential force
- Fig. 10 Variation of tangential stress σzr with distance r due to concentrated pressure source
- Fig. 11 Variation of normal stress σzz with distance r due to normal force over circular region
- Fig. 12 Variation of normal stress σzz with distance r due to tangential force over circular region
- Fig. 13 Variation of normal stress σzz with distance r due to normal force over circular region
- Fig. 14 Variation of pore pressure p with distance r due to normal force over circular region
- Fig. 15 Variation of pore pressure p with distance r due to tangential force over circular region
- Fig. 16 Variation of pore pressure p with distance r due to pressure source over circular region
- Fig. 17 Variation of tangential stress σzr with distance r due to normal force over circular region
- Fig. 18 Variation of tangential stress σzr with distance r due to normal force over circular region
- Fig. 19 Variation of tangential stress σzr with distance r due to pressure source over circular region
- Fig. 20 Variation of normal stress σzz with distance r due to normal force (frequency domain)
- Fig. 21 Variation of normal stress σzz with distance r due to tangential source (frequency domain)
- Fig. 22 Variation of normal stress σzz with distance r due to pressure source (frequency domain)
- Fig. 23 Variation of pore pressure p with distance r due to normal force (frequency domain)
- Fig. 24 Variation of pore pressure p with distance r due to tangential force (frequency domain)
- Fig. 25 Variation of pore pressure p with distance r due to pressure source (frequency domain)
- Fig. 26 Variation of tangential stress σzr with distance r due to normal force (frequency domain)
- Fig. 27 Variation of tangential stress σzr with distance r due to tangential force (frequency domain)
- Fig. 28 Variation of tangential stress σzr with distance r due to pressure source (frequency domain)
J. Cent. South Univ. (2016) 23: 1232-1242
DOI: 10.1007/s11771-016-0373-8
Interaction due to various sources in saturated porous media with incompressible fluid
Rajneesh Kumar1, Ibrahim A. Abbas2, 3, 4
1. Department of Mathematics, Kurukshetra University, Kurukshetra, Haryana, India;
2. Department of Mathematics, Faculty of Science and Arts-Khulais, University of Jeddah, Saudi Arabia;
3. Nonlinear Analysis and Applied Mathematics Research Group (NAAM), Department of Mathematics,King Abdulaziz University, Jeddah, Saudi Arabia;
4. Department of Mathematics, Faculty of Science, Sohag University, Sohag, Egypt
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract:
The disturbance due to mechanical and thermal sources in saturated porous media with incompressible fluid for two-dimensional axi-symmetric problem is investigated. The Laplace and Hankel transforms techniques are used to investigate the problem. The concentrated source and source over circular region have been taken to show the utility of the approach. The transformed components of displacement, stress and pore pressure are obtained. Numerical inversion techniques are used to obtain the resulting quantities in the physical domain and the effect of porosity is shown on the resulting quantities. All the field quantities are found to be sensitive towards the porosity parameters. It is observed that porosity parameters have both increasing and decreasing effect on the numerical values of the physical quantities. Also the values of the physical quantities are affected by the different boundaries. A special case of interest is also deduced.
Key words:
1 Introduction
The dynamic response due to various sources in a saturated porous media with incompressible fluid are of great interest in geophysics, acoustic, soil and rock mechanics and many earthquake engineering problems.
BIOT [1] derived the basic equations of poroelastisity on the basis of energy principles. PREVOST [2] rederived these equations by use of mixture theory. ZENKIEWICZ et al [3], ZENKIEWICZ and SHIOMI [4] derived the basic equations of poroelasticity by the use of principle of continuum mechanics. GATMIRI and KAMALIAN [5] adopted the later approach because it is more flexible and is based on a set of parameters with a clear physical interpretation to discuss different type of problems. GATMIRI and NGUYEN [6] investigated two-dimensional problem for saturated porous media with incompressible fluid.
GATMIRI and JABBARI [7-8] discussed time domain Green’s functions for unsaturated soil for two-dimensional and three-dimensional solutions. GATMIRI and ESLAM [9] discussed the scattering of harmonic waves by a circular cavity in a porous medium by using complex function theory approach. GATMIRI et al [10] also discussed the two-dimensional transient thermo-hydro-mechanical fundamental solution of multiphase porous media in frequency and time domains.
BAI and LI [11] obtained the solutions for cylindrical cavity in saturated thermoporoelastic medium. KAUSHAL et al [12] discussed the response of frequency domain in generalized thermoelasticity with two temperatures. KUMAR et al [13] also discussed elastodynamics of an axisymmetric problem in an anisotropic liquid-saturated porous medium. LIU et al [14] discussed the relaxation effects of a saturated porous media using the two-dimensional generalized thermoelastic theory. SUVOROV and SELVADURAI [15] derived the constitutive equations of thermo- poroelasticity by using eigenstrain-eigenstress approaches. LIU et al [16] presented a model of the equations of a generalized theory with relaxation times for a saturated porous medium and investigated a two- dimensional problem due to time-dependent thermal/ mechanical source.
OLIVEIRA et al [17] discussed boundary element formulation of axisymmetric problems for an elastic half space.The influence of the finite initial strains on the axisymmetric wave dispersion in a circular cylinder embedded in a compressible elastic medium was discussed by AKBAROV and GULIEV [18]. GORDELIY and DETOURNA [19] investigated the displacement discontinuity method for modelling axisymmetric cracks in an elastic half-space. JABBARI and DEHBANI [20-21] studied axisymmetric and spherical symmetric problems in porothermoelastic solids. ABBAS [22] studied the natural frequencies of a poroelastic hollow cylinder. For our contribution, several problems have been solved by finite element method and analytical method [23-31]. LIU and CHEN [32] studied the problem of a micromechanical analysis of the fracture properties of saturated porous media.
In the present work, the disturbance is due to concentrated source and source over circular region in the time domain and frequency domain in saturated porous media with incompressible fluid. The transformed components of displacement, stress and pore pressure are obtained and depict graphically to show the effect of porosity on the resulting quantities.
2 Governing equations
Following GATMIRI and NGUYEN [6], the field equations are as follows.
Equation of motion:
 (1)
(1)
Generalized Darcy’s law:
 (2)
(2)
Constitutive relation:
 (3)
(3)
Flow conservation for the fluid phase:
 (4)
(4)
where ui is the displacement of the solid skeleton; p denotes the fluid pressure; Wi represents the average displacement of the fluid relative to the solid. The elastic constants λ and μ are drained Lame’s constants. ρf is the fluid density; ρs is the solid density; ρ=(1-n)ρs+nρf is the density of solid-fluid mixture and m=ρf/n is the mass parameter where n is the porosity; k is the permeability coefficient. α and M are material parameters which describe the relative compressibility of the constituents. fi and γ denote the body force and the rate of fluid injection into the media, respectively.
Equations (1) and (2) with the aid of Eqs. (3) and (4) in the absence of body force and the rate of fluid injection into the media can be reduced to
 (5)
(5)
 (6)
(6)
where



3 Formulation of problem
We consider a saturated porous media with incompressible fluid whose boundaries are parallel to the plane z=0 in the cylindrical polar coordinate system (r, θ, z). We consider a two dimensional axi-symmetric problem with symmetry about z-axis, so that all the quantities are maintained independent of θ and  The complete geometry of the problem is shown in Figs. 1(a) and (b). We assume the components of displacement vector as
The complete geometry of the problem is shown in Figs. 1(a) and (b). We assume the components of displacement vector as
 (7)
(7)
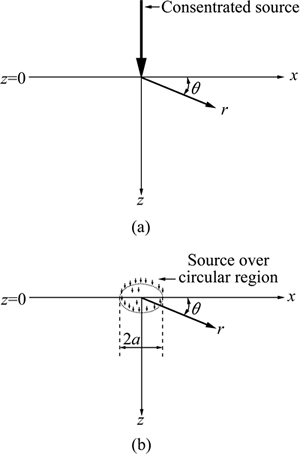
Fig. 1 Concentrated source acting on saturated porous media with incompressible fluidhalf space (a) and source over circular region acting on saturated porous media with incompressible fluid half space (b)
We define the non-dimensional quantities:
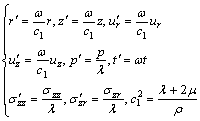 (8)
(8)
where ω is the constant having the dimensions of frequency.
The displacement components ur and uz are related to the potential functions  and
and  as
as
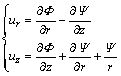 (9)
(9)
We define the Laplace and Hankel transforms as follows:
 (10)
(10)
 (11)
(11)
where Jn( ) is the Bessel function of the first kind of index n.
Making use of the dimensionless quantities defined by Eq. (8) on Eqs. (5) and (6) and with the aid of Eqs. (7) and (9) (after suppressing the prime) and applying the Laplace and Hankel transforms defined by Eqs. (10) and (11) on the resulting quantities after simplification, we obtain
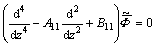 (12)
(12)
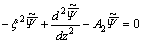 (13)
(13)
where


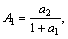
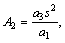






 and
and 
Using the solution of Eqs. (13) and (15) and satisfying the radial conditions that  and
and  as z→∞, we obtain the values of
as z→∞, we obtain the values of  and
and  as follows:
as follows:
 (14)
(14)
 (15)
(15)
 (16)
(16)
where m1 and m2 are given by  when n=1, 2, are the roots of Eq. (15);
when n=1, 2, are the roots of Eq. (15); 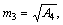 where
where  and the coupling constants are given by
and the coupling constants are given by 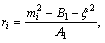 i=1, 2.
i=1, 2.
4 Boundary conditions and solution of problem
The boundary conditions at z=0 are
 (17)
(17)
where P1 and P3 are the magnitudes of the forces; P2 is the constant pressure applied on the boundary; F(r) and δ( ) are the known functions defined later in the manuscript.
Applying Laplace and Hankel transforms, we have
 (18)
(18)
The stress components are obtained with the aid of Eqs. (3), (7), (10), (11), (16) and (17) as
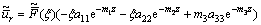 (19)
(19)
 (20)
(20)
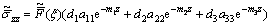 (21)
(21)
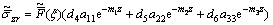 (22)
(22)
 (23)
(23)
where


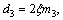

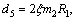
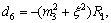






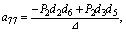



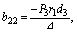

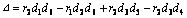 and
and 

① For normal force P2=P3=0;
② For tangential force P1=P2=0;
③ For pressure source P1=P3=0.
5 Case study
5.1 Case 1: Concentrated source
The solution due to concentrated source is obtained by substituting
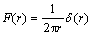 (24)
(24)
Applying Laplace and Hankel transforms on Eq. (24), we obtain

5.2 Case 2: Source over circular region
The solution due to source over the circular region of non-dimensional radius a is obtained by setting F(r)=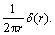 Applying Laplace and Hankel transforms on these quantities, we obtain
Applying Laplace and Hankel transforms on these quantities, we obtain
5.3 Frequency domain
In this case we assume the time harmonic behaviour as

and the boundary conditions Eq. (19) takes the form:

The expressions for displacement, stress and pore pressure in frequency domain can be obtained by replacing s by iω in the expressions of time domain Eqs. (2)-(23).
5.4 Special case
In the absence of porous incompressible fluid, the boundary conditions can be reduced to
 and the corresponding expressions for stress components in elastic half space, we obtain
and the corresponding expressions for stress components in elastic half space, we obtain
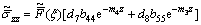 (25)
(25)
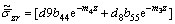 (26)
(26)
where

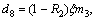



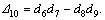
Taking P3=0 and P1=0 in Eqs.(25)-(26), we obtain respectively the stress components for the normal and tangential forces.
5.5 Numerical results and discussion
For numerical computation, the following values of the various physical parameters are taken from GATMIRI and NGUYEN [6]:
λ=12.5 MPa,μ=8.33 MPa,Ks=105 MPa,
Kf=0.22×104 MPa,ρs=2600 kg/m3,ρf=1000 kg/m3,
k=0.001 m/s, α=1, n=0.3, ω=1.
The values of normal stress σzz, tangential stress σzs and pore pressure p for fluid saturated incompressible porous medium (FSPM) and empty porous medium (EPM) are shown due to concentrated source and source applied over the circular region. The computation is carried out for two values of dimensionless time t=0.50 and t=0.75 at z=1 in the range 0≤r≤10.
The solid lines either without central symbols or with central symbols represent the variations for t=0.1, whereas the dashed lines with or without central symbols represent the variations for t=0.50. Curves without central symbols correspond to the case of FSPM whereas those with central symbols correspond to the case of EPM.
5.6 Time domain
Figure 2 shows the variation of normal stress component σzz w.r.t distance r for both FSPM and EPM due to concentrated normal force. The value of σzz first increases in the range 0≤r≤7 and then starts decreasing for FSPM as r increases and in the case of EPM, its value oscillates as r increases for both values of time.
Figure 3 shows the variation of normal stress component σzz w.r.t distance r for both FSPM and EPM due to concentrated tangential force. The value of σzz oscillates for FSPM as r increases for both values of time whereas in the case of EPM, the value of σzz starts with sharp decrease and then oscillates for both values of time as r increases.
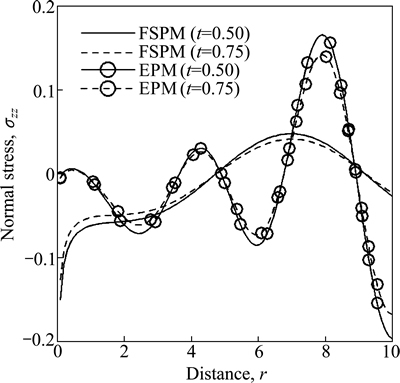
Fig. 2 Variation of normal stress σzz with distance r due to concentrated normal force
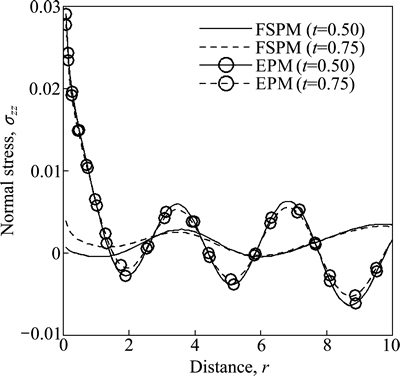
Fig. 3 Variation of normal stress σzz with distance r due to concentrated tangential force
Figure 4 shows the variation of normal stress component σzz w.r.t distance r for FSPM due to concentrated pressure source. The value of σzz is more in the range 3≤r≤6 and less in the range 6≤r≤9 for FSPM as r increases for time t=0.50 whereas for the time t=0.75 its value converges near the boundary surface.
Figure 5 shows the variation of pore pressure p w.r.t distance r for FSPM due to concentrated normal force. The value of p decreases in the range 0≤r≤3.5 and then oscillates for FSPM as r increases for time t=0.50 whereas for the time t=0.75 the value of p decreases and then oscillates as r increases.
Figure 6 shows the variation of pore pressure p w.r.t distance r for FSPM due to concentrated tangential force. The value of p decreases sharply for FSPM and then oscillates as r increases for both values of time.
Figure 7 shows the variation of pore pressure p w.r.t distance r for FSPM due to concentrated pressure source. The value of p converges near the boundary surface for FSPM as r increases for time t=0.50 whereas for the time t=0.75 the value of p increases sharply and then oscillates as r increases.

Fig. 4 Variation of normal stress σzz with distance r due to concentrated pressure source
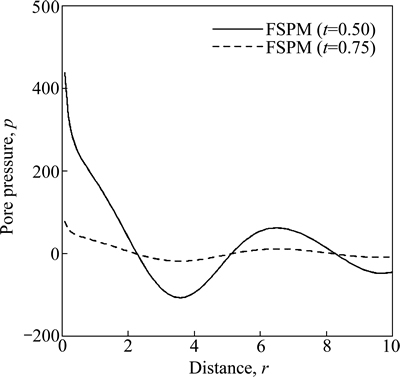
Fig. 5 Variation of pore pressure p with distance r due to concentrated normal force

Fig. 6 Variation of pore pressure p with distance r due to concentrated tangential force
Figure 8 shows the variation of tangential stress σzr w.r.t distance r for both FSPM and EPM due to concentrated normal force. The value of σzr first decreases in the range 0≤r≤3 and then oscillates for FSPM as r increases for both value of time whereas the value of σzr decreases sharply and then oscillates for EPM as r increases for both value of time.

Fig. 7 Variation of pore pressure p with distance r due to concentrated pressure source
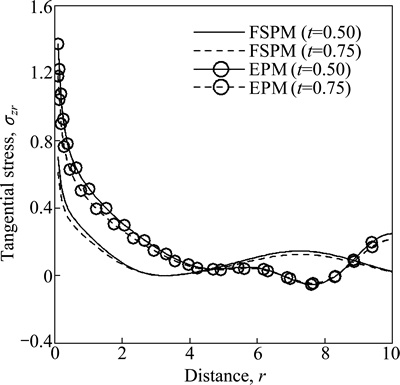
Fig. 8 Variation of tangential stress σzr with distance r due to concentrated normal force
Figure 9 shows the variation of tangential stress σzr w.r.t distance r for both FSPM and EPM due to concentrated tangential force. The value of σzr first increases monotonically and then converges near the boundary surface for FSPM and for EPM its value almost closes zero as r increases for both values of time.
Figure 10 shows the variation of tangential stress σzr w.r.t distance r for FSPM due to concentrated pressure source. The value of σzr first increases and then oscillates for FSPM as r increases for time t=0.50 whereas for the time t=0.75 the value of σzr starts with initial increase and then converges near the boundary surface.

Fig. 9 Variation of tangential stress σzr with distance r due to concentrated tangential force
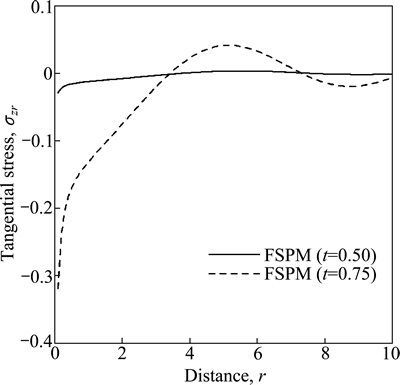
Fig. 10 Variation of tangential stress σzr with distance r due to concentrated pressure source
Figure 11 shows the variation of normal stress σzz w.r.t distance r for both FSPM and EPM due to normal force over circular region. The value of σzz first increases in the range 0≤r≤7 and then starts decreasing for FSPM as r increases and in the case of EPM, its value oscillates as r increases for both values of time.
Figure 12 shows the variation of normal stress σzz w.r.t distance r for both FSPM and EPM due to tangential force over circular region. The value of σzz starts oscillating for FSPM as r increases for both values of time and the value of σzz for EPM first decreases and then starts oscillating as r increases for both values of time.
Figure 13 shows the variation of normal stress σzz w.r.t distance r for FSPM due to pressure source over circular region. The value of σzz first increases in the range 0≤r≤6 then decreases for FSPM as r increases for both values of time.

Fig. 11 Variation of normal stress σzz with distance r due to normal force over circular region

Fig. 12 Variation of normal stress σzz with distance r due to tangential force over circular region
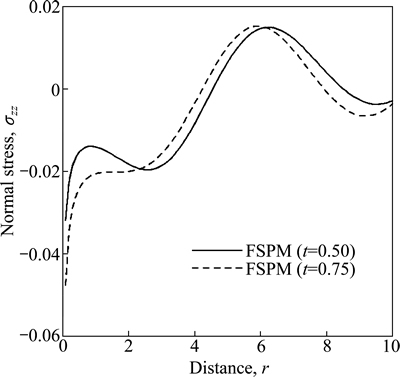
Fig. 13 Variation of normal stress σzz with distance r due to normal force over circular region
Figure 14 shows the variation of pore pressure p w.r.t distance r for FSPM due to normal force over circular region. The value of p decreases sharply in the range 0≤r≤3.5 and then oscillates as r increases for both values of time.

Fig. 14 Variation of pore pressure p with distance r due to normal force over circular region
Figure 15 shows the variation of pore pressure p w.r.t distance r for FSPM due to tangential force over circular region. The value of premain almost close to zero for FSPM as r increases for time t=0.5 whereas for the time t=0.75 the value of p decreases sharply and then oscillates as r increases.
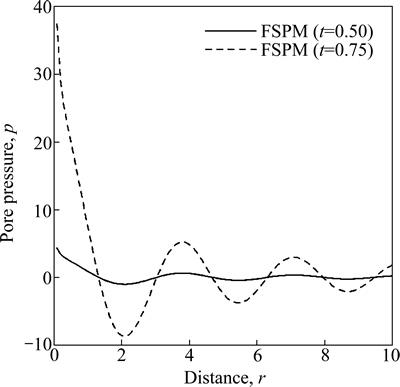
Fig. 15 Variation of pore pressure p with distance r due to tangential force over circular region
Figure 16 shows the variation of pore pressure p w.r.t distance r for FSPM due to pressure source over circular region. The value of p starts with initial increase and then oscillates for FSPM as r increases for time t=0.50 whereas for the time t=0.75 the value of p increases sharply in the range 0≤r≤5 and then starts decreasing as r increases.
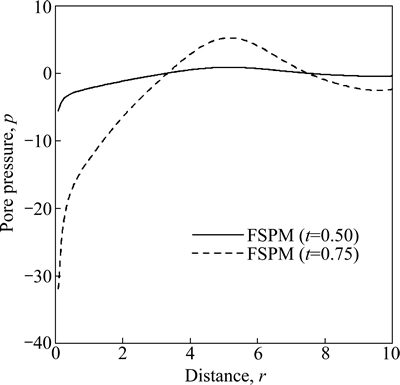
Fig. 16 Variation of pore pressure p with distance r due to pressure source over circular region
Figure 17 shows the variation of tangential stress σzr w.r.t distance r for both FSPM and EPM due to normal force over circular region. The value of σzr first decreases and then oscillates for FSPM as r increases for both value of time whereas the value of σzr decreases gradually and then oscillates for EPM as r increases for both value of time.

Fig. 17 Variation of tangential stress σzr with distance r due to normal force over circular region
Figure 18 shows the variation of tangential stress σzr w.r.t distance r for both FSPM and EPM due to tangential force over circular region. The value of σzr first increases monotonically and then remains almost close to zero for FSPM for both values of time and first increases monotonically and then converges near the boundary surface for the time t=0.75 for EPM as r increases.
Figure 19 shows the variation of tangential stress σzr w.r.t distance r for FSPM due to pressure source over circular region. The value of σzr increases sharply and then oscillates as r increases for FSPM for both value of time.

Fig. 18 Variation of tangential stress σzr with distance r due to normal force over circular region

Fig. 19 Variation of tangential stress σzr with distance r due to pressure source over circular region
5.7 Frequency domain
Figure 20 shows the variation of normal stress component σzz w.r.t distance r for both FSPM and EPM due to concentrated normal force. The value of σzz first increases monotonically in the range 0≤r≤2 and then start oscillating for FSPM as r increases for both values of time where its value oscillates as r increases for t=0.50 and converges near the boundary surface for t=0.75 for EPM.
Figure 21 shows the variation of normal stress component σzz w.r.t distance r for both FSPM and EPM due to concentrated tangential force. The value of σzz first decreases sharply and then starts oscillating for FSPM as r increases for both values of time where its value oscillates as r increases for both values of time for EPM.
Figure 22 shows the variation of normal stress component σzz w.r.t distance r for FSPM due to con-centrated pressure source. The value of σzz first decreases and then start oscillating for FSPM as r increases for both values of time.

Fig. 20 Variation of normal stress σzz with distance r due to normal force (frequency domain)

Fig. 21 Variation of normal stress σzz with distance r due to tangential source (frequency domain)

Fig. 22 Variation of normal stress σzz with distance r due to pressure source (frequency domain)
Figures 23 and 25 show the variation of pore pressure p w.r.t distance r for FSPM due to concentrated normal and pressure sources. The value of p first increases sharply in the range 0≤r≤2 and then oscillates for FSPM as r increases for both values of time.
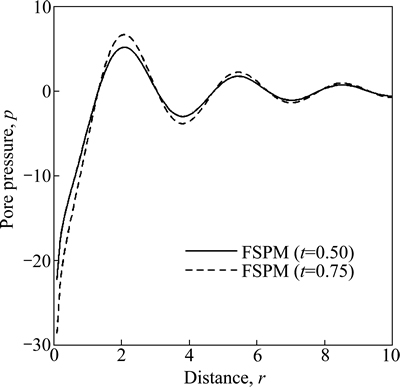
Fig. 23 Variation of pore pressure p with distance r due to normal force (frequency domain)
Figure 24 shows the variation of pore pressure p w.r.t distance r for FSPM due to concentrated tangential source. The value of p decreases and then oscillates for FSPM as r increases for both values of time.

Fig. 24 Variation of pore pressure p with distance r due to tangential force (frequency domain)
Figure 26 shows the variation of tangential stress σzr w.r.t distance r for both FSPM and EPM due to concentrated normal force. The value of σzr first increases sharply and then starts oscillating for time t=0.50 whereas for the time t=0.75, the value of σzr first increases and then converges near the boundary surface as r increases for FSPM. And for EPM it value first increases monotonically and then starts oscillating for time t=0.50 whereas for the time t=0.75 the value of σzr converges near the boundary surface as r increases.

Fig. 25 Variation of pore pressure p with distance r due to pressure source (frequency domain)

Fig. 26 Variation of tangential stress σzr with distance r due to normal force (frequency domain)
Figure 27 shows the variation of tangential stress σzr w.r.t distance r for both FSPM and EPM due to concentrated tangential source. The value of σzr decreases gradually for time t=0.50 whereas for the time t=0.75 the value of σzr first increases and then converges near the boundary surface as r increases for FSPM and for EPM it value first decreases monotonically and then starts to oscillate for time t=0.50 whereas for the time t=0.75 the value of σzr converges near the boundary surface as r increases.
Figure 28 shows the variation of tangential stress σzr w.r.t distance r for FSPM due to concentrated pressure source. The value of σzr decreases gradually and then starts oscillating for time t=0.50 whereas for the time t=0.75 the value of σzr first decreases and then converges near the boundary surface for FSPM as r increases.

Fig. 27 Variation of tangential stress σzr with distance r due to tangential force (frequency domain)

Fig. 28 Variation of tangential stress σzr with distance r due to pressure source (frequency domain)
6 Conclusions
1) In the present work, we obtain the components of displacement, stress and pore pressure due to concentrated source and source over circular region in the time domain and frequency domain in saturated porous media with incompressible fluid.
2) Near the application of the source, the porosity effect decreases the values of σzz for normal force, tangential force and pressure source where it increases the values of σzr fornormal force and tangential force but decreases the values for pressure source, due to concentrated source in the time domain.
3) In frequency domain, porosity effect increases the values of σzz, σzr and p for normal force, tangential force and pressure source for source over circular region. Also away from the source the porosity effect decreases the values of σzz for normal force and increases the values for tangential force and pressure source whereas it decreases the value of σzr for normal force and monotonically increases for tangential force and pressure source.
4) Thus, the problem analyzed is a significant problem of continuum mechanics. The results obtained as a consequence of this research work should be beneficial for researchers working on saturated porous media with incompressible fluid. By introducing various sources, the assumed model presents a more realistic model for future study.
References
[1] BIOT M A. Theory of propagation of elastic waves in fluid saturated porous solid I-low frequency range [J]. Journal of the Acoustical Society of America, 1956, 28: 168-178.
[2] PREVOST J H. Mechanics of continuous porous media [J]. International Journal of Engineering Science, 1980, 18: 787-800.
[3] ZENKIEWICZ O C, CHANG C T, BETTESS P. Drained, undrained, consolidating and dynamic behavior assumptions in soils [J]. Geotechnique, 1980, 30(4): 385-395.
[4] ZENKIEWICZ O C, SHIOMI T. Dynamic behavior of saturated porous media: The generalized Biot formulation and its numerical solution [J]. International Journal of Numerical and Analytical Methods in Geomechanics, 1984, 8: 71-96.
[5] GATMIRI B, KAMALIAN M. On the fundamental solution of dynamic poroelastic boundary integral equations in the time domain [J]. The International Journal of Geomechanics, 2002, 2(4): 381-398.
[6] GATMIRI B, NGUYEN K V. Time 2D fundamental solution for saturated porous media with incompressible fluid [J]. Commun Numer Methods Eng, 2005, 21: 119-132.
[7] GATMIRI B, JABBAR I. Time domain Green’s functions for unsaturated soil. Part I: 2-D solution [J]. International Journal of Solid and Structure, 2005, 42: 5971-5990.
[8] GATMIRI B, JABBAR I. Time domain Green’s functions for unsaturated soil. Part II: 3-D solution [J]. International Journal of Solid and Structure, 2005, 42: 5991-6002.
[9] GATMIRI B, ESLAM I. The scattering of harmonic waves by a circular cavity in a porous medium: Complex function theory approach [J]. International Journal of Geomechanics, 2007, 7(5): 371-381.
[10] GATMIRI B, MAGHOUL P, DUHAMEL D. Two-dimensional transient thermo-hydro-mechanical solutions of multiphase porous media in frequency and time domain [J]. International Journal of Solid and Structure, 2010, 47: 595-610.
[11] BAI B, LI T. Solutions for cylindrical cavity in saturated thermoporoelastic medium [J]. Acta Mechanica Solida Sinica, 2009, 22(1): 85-94.
[12] KAUSHAL S, KUMAR R, MIGLANI A. Responce of frequency domain in generalized thermoelasticity with two temperature [J]. Journal of Engineering Physics and Thermophysics, 2010, 83(5): 1080-1088.
[13] KUMAR R, GARG N R, MIGLANI A. Elastodynamics of an axisymmetric problem in an anisotropic liquid-saturated porous medium [J]. Journal of Sound and Vibration, 2003, 261: 697-714.
[14] LIU G, DING S, YE R, LIU X. Relaxation effects of a saturated porous media using the two dimensional generalized thermoelastic theory [J]. Transp Porous Med, 2011, 86: 283-303.
[15] SUVOROV A P, SELVADURAI A P S. Macroscopic constitutive equations of thermo-poroelasticity by using eigenstrain-eigenstress approaches [J]. Philosophical Magazine, 2011, 91(18): 2317-2342.
[16] LIU G, DING S, YE R, LIU X. Relaxation effects of a saturated porous media using the two-dimensional generalized thermoelastic theory [J]. Transp Porous Med, 2011, 86: 283-303.
[17] OLIVEIRA M M F, DUMONT N A, SELVADURA A P S. Boundary element formulation of axisymmetric problems for an elastic half space [J]. Engineering Analysis with Boundary Elements, 2012, 36(10): 1478-1492.
[18] AKBAROV S D, GULIEV M S. The influence of the finite initial strain on the axisymmetirc wave dispersion in a circular cylinder embedded in a compressible elastic medium [J]. International Journal of Mechanical Science, 2010, 52(1): 89-95.
[19] GORDELIY E, DETOURNA E. Displacement discontinuity method for modeling axisymmetric cracks in an elastic half-space [J]. International Journal of Solids and Structures, 2011, 48(19): 2614-2629.
[20] JABBARI M, DEHBANI H. An exact solution for classic coupled thermoelasticity in axisymmetric cylinder [J]. Journal of Solid Mechanics, 2010, 2(2): 129-143.
[21] JABBARI M, DEHBANI H. An exact solution for quasi-static poro-thermoelasticity in spherical coordinate [J]. Iranian Journal of Mechanical Engineering, 2011, 12(1): 86-108.
[22] ABBAS I. Natural frequencies of a poroelastic hollow cylinder [J]. Acta Mechanica, 2006, 186(1/2/3/4): 229-237.
[23] OTHMAN M I, ABBAS I A. Effect of rotation on plane waves in generalized thermomicrostretch elastic solid: Comparison of different theories using finite element method [J]. Canadian Journal of Physics, 2014, 92(10): 1269-1277.
[24] ABBAS I A, ZENKOUR A M. Dual-phase-lag model on thermoelastic interactions in a semi-infinite medium subjected to a ramp-type heating [J]. Journal of Computational and Theoretical Nanoscience, 2014, 11(3): 642-645.
[25] ABBAS I A, KUMAR R, REEN L S. Response of thermal source in transversely isotropic thermoelastic materials without energy dissipation and with two temperatures [J]. Canadian Journal of Physics, 2014, 92(11): 1305-1311.
[26] ABBAS I A, KUMAR R. Deformation due to thermal source in micropolar generalized thermoelastic half-space by finite element method [J]. Journal of Computational and Theoretical Nanoscience, 2014, 11(1): 185-190.
[27] ABBAS I A. Eigenvalue approach in a three-dimensional generalized thermoelastic interactions with temperature-dependent material properties [J]. Computers & Mathematics with Applications, 2014, 68(12): 2036-2056.
[28] KUMAR R, GUPTA V, ABBAS I A. Plane deformation due to thermal source in fractional order thermoelastic media [J]. Journal of Computational and Theoretical Nanoscience, 2013, 10(10): 2520-2525.
[29] KUMAR R, ABBAS I A. Deformation due to thermal source in micropolar thermoelastic media with thermal and conductive temperatures [J]. Journal of Computational and Theoretical Nanoscience, 2013, 10(9): 2241-2247.
[30] BAI B, LI T. Irreversible consolidation problem of a saturated porothermoelastic spherical body with a spherical cavity [J]. Applied Mathematical Modelling, 2013, 37: 1973-1982.
[31] ABBAS I A. Generalized thermoelastic interaction in a functional graded material with fractional order three-phase lag heat transfer [J]. Journal of Central South University. (In press)
[32] LIU Ming-chao, CHEN Chang-qing. A micromechanical analysis of the fracture properties of saturated porous media [J]. International Journal of Solids and Structures, 2015, 63: 32-38.
(Edited by DENG Lü-xiang)
Received date: 2015-01-27; Accepted date: 2015-05-20
Corresponding author: Rajneesh Kumar, PhD; E-mail: Rajneesh_kuk@rediffmail.com
Abstract: The disturbance due to mechanical and thermal sources in saturated porous media with incompressible fluid for two-dimensional axi-symmetric problem is investigated. The Laplace and Hankel transforms techniques are used to investigate the problem. The concentrated source and source over circular region have been taken to show the utility of the approach. The transformed components of displacement, stress and pore pressure are obtained. Numerical inversion techniques are used to obtain the resulting quantities in the physical domain and the effect of porosity is shown on the resulting quantities. All the field quantities are found to be sensitive towards the porosity parameters. It is observed that porosity parameters have both increasing and decreasing effect on the numerical values of the physical quantities. Also the values of the physical quantities are affected by the different boundaries. A special case of interest is also deduced.
- Interaction due to various sources in saturated porous media with incompressible fluid


