Discussion and prediction on decreasing flow stress scale effect
SHEN Yu(申 昱), YU Hu-ping(于沪平), RUAN Xue-yu(阮雪榆)
National Die and Mold CAD Engineering Research Center, Shanghai Jiaotong University,
Shanghai 200030, China
Received 17 May 2005; accepted 6 September 2005
Abstract:
Based on crystal plasticity theory and surface layer model, relation of flow stress to billet dimension and grain size was built, and rationality of derived relation was verified with tensile tests of different size billets. With derived expressions, relation of decreasing flow stress scale effect to billet dimension, grain size as well as billet shape was discussed and predicted. The results show that flow stress is proportional to billet size; with decrease of grain size, flow stress is less influenced by billet dimension. When both cross section area and grain size are same, flow stress decrease of rectangular section billet or sheet is larger than that of circular section billet.
Key words:
microforming; flow stress; scale effect; billet dimension; crystal plasticity theory; surface layer model; Hall-Petch relation;
1 Introduction
With the continuous development of science and technology, especially the rapid progress of electronic industry and micromachine, microparts are needed more and more, and their technical requirements are higher and higher[1]. Under such circumstance, in 1990s, microforming technology came into being, that is, traditional plastic forming process was applied to micro scale to produce batch micro metal parts. As a completely new plastic processing technology, microforming is a such technology that is used to produce parts with at least submillimetre in two dimensions by plastic deformation of materials[2]. The typical processes of microforming can be classified into micro extrusion, micro sheet metal, micro die forging, etc. Up to now, this technology has been partially used in electronic industry for the production of microparts like micro screws, contact springs and IC socket etc. With the continuous development of technologies, applied fields of microforming are rapidly extended to machinery, chemical industry, aerospace, biology, etc, and its status is more and more important in these fields.
However, existing studies[3－9] show that during microforming, with the downscaling of billet dimension, flow stress is very sensitive to billet dimension, and a series of explicit scale effects emerge, which result in the failure of traditional (macro) forming process and theories. As a result, scale effects have been the bottleneck of microforming technology. Of these scale effects, decreasing flow stress scale effect, which is defined as decrease of flow stress with the downscaling of billet size, results in the disability of transition in traditional forming process and theory to micro scale, so design of microforming process and die is influenced, even the development and application of microforming are hindered.
Just due to reasons mentioned above, up to now, there have been some studies on decreasing flow stress scale effect[11－13]. ENGEL and EGERER[7] as well as GEIGER and ECKSTEIN[3] did upsetting test with different size small cylinder billets and found that flow stress of billet is decreased with the downscaling of billet size. Similarly, Raulea et al[10] studied how microforming process is affected by the ratio of grain size to sheet thickness, and found that along the direction of sheet thickness, with the decrease of grain quantity(at least one grain), yield strength of material is decreased remarkably. To this kind of scale effect, ENGEL and ECKSTEIN[9] explained with surface layer model: for microparts, the share of grains representing the surface layer becomes high compared to the grains that are surrounded entirely by other grains. From metal physics theory it is known that free surface grains show less hardening compared with the inner volume grains which can be explained by the different mechanisms of dislocation movement and pile-up and by the fact that they are less subjected to compatibility restrictions. Thus, the integral flow stress that is measured in upsetting or tensile tests is a function of the share of surface grains. This share increases with grain size and with miniaturization.
It can be seen from existing studies that surface layer model can explain the decreasing flow stress scale effect phenomena well. However, in order to study this kind of scale effect more thoroughly and systematically, to find relation of flow stress to billet dimension and grain size, even to predict and control this scale effect, to provide relevant information for design of microforming process and die, in this study, based on crystal plasticity theory and surface layer model, decreasing flow stress scale effect was discussed and predicted.
2 Relation of flow stress to billet dimension and grain size
It is considered by surface layer model[9] that as dislocations can not be stored on free surface of billet, and grains on free surface are less constrained, flow stress near free surface is lower than that of inner part. Therefore, the whole flow stress of billet can be regarded as a weighted average of the inner grains and the outer grains flow stresses, and expression of flow stress is shown below[9]:
(1)
(2)
where 
is flow stress of billet, 
and 
are inner grains area fraction and inner grains flow stress of billet cross section respectively; 
and 
are surface layer grains area fraction and surface layer grains flow stress of billet cross section respectively. Here is equivalent to flow stress of polycrystal, namely traditional flow stress, and is equivalent to flow stress of single grain.
By substituting Eqn.(2) into Eqn.(1) and simplifying, one can obtain
(3)
In addition, it is known from crystal plasticity theory, that traditional grain diameter d and flow stress of billet satisfy Hall-Petch equation[14－16]:
(4)
where coefficients σ0 and K denote the resistance of dislocation movement in grain and the influence of neighboring grains respectively. Therefore, it can be regarded that σ0 is equivalent to flow stress of single grain, equal to , and σ=σ0+Kd－1/2 is traditional flow stress, equal to . By substituting Hall-Petch equation and σ0 into Eqn.(3), one can obtain
(5)
Now consider coefficient . According to definition of mentioned above, can be expressed as
(6)
where C is circumference of billet cross section, and A is cross section area of billet. By substituting Eqns.(2) and (6) into Eqn.(5), one can obtain
(7)
It can be seen from Eqn.(7) that not only flow stress is closely related to grain size, but also dimension and shape of billet.
3 Experimental verification
In order to verify the rationality of flow stress expression Eqn.(7) derived above, according to specification of national standard GB/T 228－2002[17], tensile tests were performed with different diameter copper wire. In order to remove work hardening and observe scale effect more clearly, tested billets were heated in inert gas to grow equiaxed grains. Billet dimensions and scale factors are shown in Table 1.
Table 1 Experimental parameters
Tests were done at ambient temperature with Zwick/Roell Z020 universal test machine which has 1μm displacement precision and 0.5％ load preci- sion. The loading speed was quasistatic. During testing process, load was recorded at fixed time interval, and the whole test equipment are shown in Fig.1.
Through the disposal to load-displacement data obtained from tests, flow stress-logarithmic strain curves of different diameter billets were obtained, shown in Fig.2.
Fig.1 Equipment of tensile test
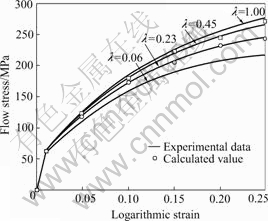
Fig.2 Curves of flow stress—logarithmic strain
Under the condition of same grain size and strain, by use of Eqn.(7) and flow stress-logarithmic strain curves of 
=1 and =0.06 obtained from tests, flow stress-logarithmic strain curves of =0.45 and =0.23 were calculated, and comparison with test curves is shown in Fig.2.
It is obvious that calculated results with Eqn.(7) are well fitted with experimental data, which sufficiently illustrates the rationality of expression built above.
4 Discussion and prediction of decreasing flow stress scale effect
It can be seen from above derivation that flow stress is not only related to grain size, but also dimension and shape of billet. Therefore, based on expression built above, decreasing flow stress scale effect was discussed and predicted from aspects like billet dimension, grain size, as well as shape of billet etc.
4.1 Influence of billet dimension
In order to discuss influence of billet dimension on flow stress conveniently, according to Eqn.(7), the concept of scale effect factor 
was introduced:
(8)
By substituting Eqn.(8) and Hall-Petch equation into Eqn.(7), one can obtain
(9)
where 
is flow stress of traditional macro scale, and coefficient 
, which is relevant to grain diameter, denotes sensitivity of flow stress on scale effect factor. Relation of flow stress to scale effect factor is shown in Fig.3.
Fig.3 Relation of flow stress to scale effect factor
It can be found from Fig.3 that with the increase of scale effect factor η, that is with the decrease of billet dimension, flow stress is linearly decreased, and decreasing flow stress scale effect is gradually emerged; when billet is in macro scale, namely when η→0, σf =σ, namely flow stress of traditional macro scale, which is irrelevant to billet dimension, so decreasing flow stress scale effect vanishes.
It is also known from Eqn.(9) that decreasing velocity of flow stress is determined by coefficient 
, which is a function of grain diameter and increases with the increase of grain size. When grain size is tiny, approaches 0, and Eqn.(9) is changed into a horizontal line σf =σ, thus no decreasing flow stress scale effect is emerged; when grain size is increased, is gradually increased, and decreasing velocity of flow stress is increased, namely under same billet dimension, flow stress is decreased more, so decreasing flow stress scale effect is more remarkable.
4.2 Influence of grain size
Similarly, according to Eqn.(9), when billet dimension is constant, relation of flow stress to grain size has not been the traditional relation governed by Hall-Petch equation, shown in Fig.4.
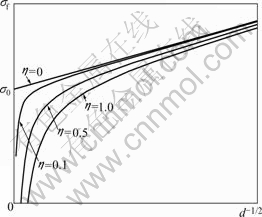
Fig.4 Relation of flow stress to grain size
It can be found from Fig.4 that with the increase of grain size, flow stress is gradually decreased. Through the comparison of curves with different billet size, it can also be seen that with the increase of billet dimension, decreasing speed of flow stress is gradually decreased, till constant K, namely decreasing flow stress scale effect is gradually weakened with increasing billet dimension, which is consistent with Fig.3.
It can also be found that with the decrease of grain size, difference of flow stress between different size billets is decreased, namely decreasing flow stress scale effect is not remarkable; when grain size is approaching 0, decreasing flow stress scale effect disappears, that is flow stress is irrelevant to billet dimension. Therefore, decreasing flow stress scale effect can be controlled by decreasing grain size.
4.3 Influence of billet shape
According to Eqn.(8), namely the definition of scale effect factor, the decreasing flow stress scale effect is also influenced by billet shape. The influence of usual cross section shape on this kind of scale effect was discussed below.
4.3.1 Circular cross section
For circular cross-section billet with diameter D, its scale effect factor is
Accordingly, flow stress is changed into
(11)
4.3.2 Rectangular cross section
For rectangular cross section with thickness δ and width b, its scale effect factor is
(12)
Accordingly, flow stress is changed into
(13)
Further, when b is much larger than thickness δ, namely billet is sheet, scale effect factor is changed into
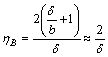(14)
Accordingly, flow stress is changed into
(15)
4.3.3 Influence of cross section shape
Consider circular and rectangular cross section with same area A, there are below equations:
Circular cross section:
(16)
Rectangular cross section:
(17)
Consider expression 
:
(18)
and
≤
(19)
By substituting Eqns.(16) and (17) into Eqn.(19), and simplifying yields
≤
＜1 (20)
It can be found that under the same cross section area and grain size, flow stress decrease of rectangular cross section billet or sheet is bigger than that of circular cross section billet, namely the decreasing flow stress scale effect is more liable to happen.
5 Conclusions
1) In micro scale, flow stress is not only related to grain size, but also billet size and shape.
2) Under the condition of constant grain size, flow stress is proportional to billet size.
3) With decrease of grain size, flow stress is less influenced by billet dimension, that is decreasing flow stress scale effect is gradually weakened.
4) Billet shape has a significant influence on decreasing flow stress scale effect. Under the condition of same cross section area and grain size, flow stress decrease of rectangular cross section billet or sheet is larger than that of circular cross section billet, and decreasing flow stress scale effect is more liable to happen.
5) What has been done in this paper theoretically contributes to the further control of this scale effect as well as the design of process and die in microforming.
References
[1] GEIGER M, ENGEL U, VOLLERTSEN F, ROLAND K, ARTHUR M. Metal forming of micro parts for electronics [J]. Production Engineering, 1994, 2(1): 15－18.
[2] GEIGER M, KLEINER M, ECKSTEIN R, TIESLER N, ENGEL U. Microforming [J]. Annals of the CIRP, 2001, 50(2): 445－462.
[3] GEIGER M, ECKSTEIN R. Microforming[A]. Kiuchi M, Nishimura h, Yanagimoto j. Advanced Technology of Plasticity[C]. Japan: Yokohama, 2002. 327－338.
[4] GEIGER M, ENGEL U. Microforming-a challenge to the plasticity research community-addressed to the 40th anniversary of the JSTP [J]. Journal of the JSTP, 2002, 43(494): 171－172.
[5] TIESLER N, ENGEL U. Microforming-effects of miniaturization [A]. Pietrzyk. Metal Forming 2000[C]. Rotterdam: Balkema, 2000. 355－360.
[6] GEIGER M, VOLLERTSEN F, KALS R. Fundamentals on the manufacturing of sheet metal microparts [J]. Annals of the CIRP, 1996, 45(1): 277－282.
[7] ENGEL U, EGERER E. Basic research on cold and warm forging of microparts [J]. Key Engineering Materials, 2003, 236(1): 449－456.
[8] TIESLER N, ENGEL U, GEIGER M. Basic Research on Cold Forming of Microparts[A]. Kiuchi m, Nishimura h, Yanagimoto j. Advanced Technology of Plasticity[C]. Japan: Yokohama, 2002. 379－384.
[9] ENGEL U, ECKSTEIN R. Microforming-from basic research to its realization [J]. Journal of Materials Processing Technology, 2002(1): 35－44.
[10] RAULEA L. V, GOVAERT L.E, BAAIJENS F P T. Grain and specimen size effects in processing metal sheets[A]. GEIGER M. Advanced Technology of Plasticity[C]. Nuremberg: Springer, 1999. 939－944.
[11] PICART P, MICHEL J F. Effects of size and texture on the constitutive behaviour for very small components in sheet metal forming [A]. GEIGER M. Advanced Technology of Plasticity[C]. Nuremberg: Springer, 1999. 895－900.
[12] KOCA?DA A, PREJS T. The effect of miniaturization on the final geometry of the bent products[A]. Pietrzyk. Metal Forming 2000[C]. Rotterdam: A. A. Balkema, 2000, 375－378.
[13] RICHELSEN A B, VAN DER GIESSEN E. Size effects in sheet drawing [A]. 9th International Conference on Sheet Metal [C]. Belgium: Leuven, 2001. 263－270.
[14] Polusion. Physical Basis of Plastic Deformation [M]. HUANG Ke-qin. Beijing: Metallurgical Industry Press, 1989. 225－230.(in Chinese)
[15] Yang Jue-xian. Physical Basis of Metal Plastic Deformation[M]. Beijing: Metallurgical Industry Press, 1988. 105－134.(in Chinese)
[16] CHEN Li-qing, KANETAKE N. Finite element polycrystal model simulation of cold rolling textures in deformation processed two-phase Nb/Al metal-metal composites [J]. Trans Nonferrous Met Soc China, 2005, 15(1): 64－71.
[17] GB/T 228-2002, Metallic materials–Tensile testing at ambient temperature [S].
Corresponding author: SHEN Yu; Tel: +86-21-62934611; E-mail: shenyu@sjtu.edu.cn
(Edited by LI Xiang-qun)
