一种新的考虑柔顺度要求的结构拓扑优化方法
易继军1, 2,荣见华2,曾韬1
(1. 中南大学 机电工程学院,湖南 长沙,410083
2. 长沙理工大学 汽车与机械工程学院,湖南 长沙,410004)
摘要:为了解决拓扑优化分析计算量大和材料分布等问题,提出一种不影响算法收敛性的设计空间调整手段。针对体积约束和柔顺度最小的结构拓扑优化问题,采用变体积约束限的方法控制柔顺度变化的步长,然后,根据优化准则法,提出一种新的考虑柔顺度要求的结构拓扑优化方法。研究结果表明:该方法具有较高的求解效率,同时能够获得较好0~1分布特征的优化拓扑。
关键词:
中图分类号:TH122 文献标志码:A 文章编号:1672-7207(2011)07-1953-07
A new structural topology optimization method subject to compliance
YI Ji-jun1, 2, RONG Jian-hua2, ZENG Tao1
(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
2. School of Automobile and Mechanic Engineering, Changsha University of Science and Technology,
Changsha 410004, China)
Abstract: Based on the fact that the structural domain need be divided into some finite element meshes when structural topology optimization is made, and some optimization problems may need a large finite element mesh, a new structural topology optimization method was proposed. The minimum compliance topology optimization of continuum structures was dealt with volume constraint. The moving of compliance and process of iteration were controlled by the varying volume constraint, an optimality criteria was incorporated, and a new structural topology optimization method subject to compliance was proposed. The results show that the proposed method has higher efficiency, and is robust and practicable, making the optimum structure obtained with 0-1 distribution material property.
key words: topology optimization; compliance; volume constraint; design space adjustment; optimality criteria
连续体结构拓扑优化方法主要有均匀化方法[1-2] (Homogenization)、实体各向同性材料惩罚法[3-4](Solid isotropic material with penalization, SIMP)、渐进结构优化方法[5-6](Evolutionary structural optimization, ESO)、水平集方法[7-8] (Level set method)、独立连续拓扑变量及映射变换方法(Independent continuous mapping, ICM)[9-10]和拓扑描述函数法(Topology description function, TDF)[11]等。SIMP法及ICM方法将拓扑优化问题转化为材料分布问题来处理,因此,需要将最终求得的材料布局解释为待求的结构拓扑。另外,采用ICM法和SIMP法,在迭代优化过程中,被删除的大量材料单元仍以较小的刚度和质量存在于结构中,一方面,易引起结构总刚度矩阵病态以及结构出现虚假的局部模态;另一方面,结构分析的规模始终保持为最大设计域的规模,其分析计算量大。为了解决上述问题,本文作者针对体积约束和柔顺度最小的结构拓扑优化问题,首先采用有理分式材料模型,建立结构刚度矩阵与拓扑变量的关系,然后,根据优化准则法 (OC)[12],提出一种考虑柔顺度要求和基于设计空间调整的结构拓扑优化方法。
1 单元拓扑变量与过滤函数
1.1 单元拓扑变量
类似于ICM方法,设置第i号单元的拓扑变量为ti。当拓扑变量ti=0时,表示该单元不存在;当拓扑变量ti=1时,表示该单元存在;当拓扑变量0<ti<1时,表示该单元为从无到有的过渡状态。
1.2 过滤函数
用过滤函数fv(ti)和fk(ti)识别单元体积和单元刚度,单元性质参数识别采用如下公式:
![]() (1)
(1)
其中:Vi和[Ki]分别表示拓扑变量为ti对应的单元体积和单元刚度矩阵;![]() 和
和![]() 分别表示单元固有体积和单元固有的刚度矩阵。这里取
分别表示单元固有体积和单元固有的刚度矩阵。这里取![]() 。
。
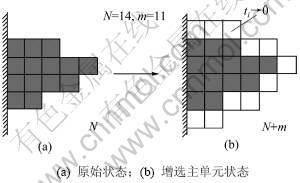
为了有利于设计空间减缩和扩展的实现,过滤函数fk(ti)必须合理地设计。设计空间灵敏度反映新的设计变量增加对目标函数或约束条件的影响[13]。因为设计空间的变化数学上是一个不连续的过程,Kim等采用增选主单元状态和方向导数计算了设计空间灵敏 度[14]。图1所示为设计空间的一个增选主单元状态,在结构周边引入一层接近于0的低密度材料单元,而这些单元的增添对目标函数或约束条件影响很小。本文在设计空间扩展时采用类似的措施(引入一层人工材料单元),而在设计空间减缩时,将一些具有很小拓扑变量的材料单元从结构上去掉,这些单元的删除对目标函数或约束条件影响也是很小的。
图1 增选主单元状态概念
Fig.1 Concept of pivot phase
设计空间灵敏度的定义,要求fk(ti)具有下列特性:
![]() (2)
(2)
注意到将用于设计变量灵敏度的典型函数![]() ,用于设计空间灵敏度是不稳定的。因为它在ti=0处斜率为0。参考Stolpe和Svanberg提出的有
,用于设计空间灵敏度是不稳定的。因为它在ti=0处斜率为0。参考Stolpe和Svanberg提出的有
理分式材料模型[15],设![]() ,则
,则![]() 具有式(2)的特性。
具有式(2)的特性。
2 设计空间的缩减和扩展
将结构分为可设计和不可设计区域,设可设计区域的单元数为P,其单元编号可设为ip(p=1, 2, …, P),可设计单元的拓扑变量![]() 在迭代计算中在0到1之间变化;不可设计区域的单元数为Q,其单元编号可设为nq(q=1, 2, …, Q),不可设计单元的拓扑变量
在迭代计算中在0到1之间变化;不可设计区域的单元数为Q,其单元编号可设为nq(q=1, 2, …, Q),不可设计单元的拓扑变量![]() 在迭代计算中不变。
在迭代计算中不变。
因此,将具有体积约束的最小柔顺度的拓扑优化问题写为:
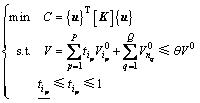 (3)
(3)
其中:V0为整个设计域的初始体积;![]() 为第n个单元固有体积;θ(0<θ<1)为优化目标体积比;V为优化
为第n个单元固有体积;θ(0<θ<1)为优化目标体积比;V为优化
后的结构体积。类似于SIMP方法,这里设置非零的下限![]() ,以确保优化过程中减缩有限单元模型规模后结构仍保持非奇异。
,以确保优化过程中减缩有限单元模型规模后结构仍保持非奇异。
另外,为了使迭代中的优化拓扑有较好的0~1分布特征,同时两相邻迭代步的优化拓扑变化较小,这里采用以体积约束限渐进的方式,将模型(3)转化为变体积约束限的系列模型(4)进行求解。这种变体积约束限的求解模式使柔顺度小量变化,又能使拓扑设计变量在某一小邻域移动,且具有较好的0~1分布特征。
 (4)
(4)
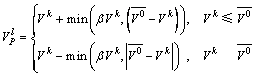 (5)
(5)
其中:![]() ;β为体积约束限变化因子,
;β为体积约束限变化因子,
可在0.01~0.10间取值;Vk为第k迭代步的结构拓扑体积;![]() (l=1, 2, …, J)在一轮优化迭代中不变,且在下一轮迭代时按式(5)变化。
(l=1, 2, …, J)在一轮优化迭代中不变,且在下一轮迭代时按式(5)变化。
为了易于求解具有较大规模有限元网格模型的优化问题,这里采用一些优化迭代步将拓扑变量很小的单元从结构上去掉,而其他单元拓扑变量不变的策
略。即设置![]() ,使得
,使得![]() <
<![]() <
<![]() (p=1, 2, …, P),ε为一小量。把每个可设计的保留单元的拓扑变量
(p=1, 2, …, P),ε为一小量。把每个可设计的保留单元的拓扑变量![]()
与阈值![]() 相比较来确定单元是否存在的状态,基于方程(6),挑选用于单元删除的最潜在的候选单元,即将这些单元看成将要消失的单元。
相比较来确定单元是否存在的状态,基于方程(6),挑选用于单元删除的最潜在的候选单元,即将这些单元看成将要消失的单元。
![]() (6)
(6)
为了确保优化迭代中的结构非奇异,使优化迭代正常进行,同时,结构优化时具有设计空间的扩展(增添单元)功能。这里采用在结构边界和孔洞周围附加人工材料单元的办法来确保结构刚度矩阵非奇异。人工材料单元附加的具体方法见文献[5, 15]。这里将人工材料单元的弹性模量设为占据该空间的原始材料单元的弹性模量,仅将人工材料单元的拓扑变量取为![]() ,人工材料单元参与结构参数计算和优化迭代。根据人工材料单元拓扑变量的变化情况,对设计空间进行扩展(即增添单元)。设增添单元的阈值为
,人工材料单元参与结构参数计算和优化迭代。根据人工材料单元拓扑变量的变化情况,对设计空间进行扩展(即增添单元)。设增添单元的阈值为![]() ,基于方程(7),挑选用于单元增添的最潜在的候选单元,即将这些单元看成将要增添的单元。
,基于方程(7),挑选用于单元增添的最潜在的候选单元,即将这些单元看成将要增添的单元。
![]() (7)
(7)
设计空间缩减和扩展的准则表为:
![]() ≤
≤![]() ,
,![]() (8)
(8)
式中:nd和na分别为集合Nd和Na的单元个数;![]() ,
,![]() 和
和![]() 为小的经验参数值。
为小的经验参数值。
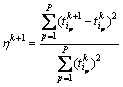 (9)
(9)
若式(8)成立,则执行式(10)和(11)的操作:
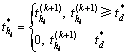 (10)
(10)
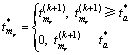 (11)
(11)
当执行式(10)和(11)的操作后,非零的![]() 所对应的单元材料特性参数编号变为保留单元的特性参数编号,为零的
所对应的单元材料特性参数编号变为保留单元的特性参数编号,为零的![]() 所对应的单元材料特性参数编号变为无材料单元所对应的特性参数编号。若式(8)成立,则执行式(10)和(11)的操作,这一轮的拓扑优化就完成了设计空间的减缩和扩展,否则,该轮拓扑优化不进行设计空间的减缩和扩展。若结构有对称性要求,每轮迭代需对所有拓扑变量ti进行对称性处理。
所对应的单元材料特性参数编号变为无材料单元所对应的特性参数编号。若式(8)成立,则执行式(10)和(11)的操作,这一轮的拓扑优化就完成了设计空间的减缩和扩展,否则,该轮拓扑优化不进行设计空间的减缩和扩展。若结构有对称性要求,每轮迭代需对所有拓扑变量ti进行对称性处理。
当优化迭代求解接近最优结构时,满足式(6)的单元已经很少,此时,适当提高![]() ,对于满足条件的单元执行式(12)和(13)的操作:
,对于满足条件的单元执行式(12)和(13)的操作:
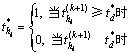 (12)
(12)
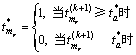 (13)
(13)
3 灵敏度分析
在有限元分析中结构静平衡方程可表示成:
![]() (14)
(14)
结构柔顺度可写为:
![]() (15)
(15)
对方程(15)求导得到:
![]() (16)
(16)
因为[K]-1是对称矩阵,由方程(16)可得到:
![]() (17)
(17)
因为设计变量ti仅与第i号单元相关,因此,方程(17)可写为:
![]() (18)
(18)
考虑ti作为变量变化,第i号单元刚度矩阵的导数可表示为:
![]() (19)
(19)
将方程(19)代入方程(18)得到:
![]() (20)
(20)
体积对设计变量ti的导数为:
![]() (21)
(21)
4 优化模型的求解
拓扑优化问题式(4)的Lagrangian函数为:
![]()
![]() (22)
(22)
当t取极值t*时,上述Lagrangian函数满足K-T条件:
 (23)
(23)
式(23)又可写为:
 (24)
(24)
将方程(20)和(21)代入方程(24)中的第1式得:
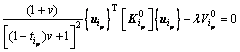 (25)
(25)
即
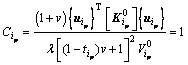 (26)
(26)
令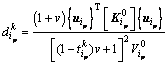 ,则
,则![]() 。将方程(26)作为优化设计准则,得到基于优化准则法的迭代公式如下:
。将方程(26)作为优化设计准则,得到基于优化准则法的迭代公式如下:
 (27)
(27)
式中:![]() 为阻尼系数,引入
为阻尼系数,引入![]() 的目的是为了确保数值计算的稳定性和收敛性。
的目的是为了确保数值计算的稳定性和收敛性。
5 拉格朗日乘子的计算
用方程(27)进行设计变量的更新需求解![]() ,而求解
,而求解![]() 需先求得拉格朗日乘子
需先求得拉格朗日乘子![]() 。
。
假设当迭代计算由第k步更新到第k+1步时,结构体积由![]() 变化到
变化到![]() 。
。
令![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,由式(21)可得:
,由式(21)可得:
![]()
![]() (28)
(28)
由方程(26),(27)和(28)整理得方程(29),即可求解![]() 。
。
![]()
![]() (29)
(29)
6 算例
6.1 一端面固支的短悬臂梁结构拓扑优化设计
如图2所示是一根短悬臂梁的经典例子。左端固定,梁的尺寸是Lx=0.16 m,Ly=0.10 m,厚度t=0.02 m,在自由端面中部20 mm长区域铅垂方向施加F= 50 kN/m的均布线载荷(为了避免应力集中和计算结果与划分网格的关联度大,所有算例均采用均布载荷);弹性模量E=210 GPa,泊松比![]() =0.3,密度为7.8 t/m3。初始设计区域为0.16 m×0.10 m×0.02 m的立体区域,将其划分为80×50×2即8 000个八节点六面体单元网格。为了评价结构拓扑的性能,Liang等[16]提出了性能指标的概念。文献[17]中拓扑的性能指标PI=1.253 3[18],而采用本文的方法得到拓扑PI= 1.275 5。这表明本文的方法得到拓扑结构性能比文献[17]中的优,同时它的计算效率更高。
=0.3,密度为7.8 t/m3。初始设计区域为0.16 m×0.10 m×0.02 m的立体区域,将其划分为80×50×2即8 000个八节点六面体单元网格。为了评价结构拓扑的性能,Liang等[16]提出了性能指标的概念。文献[17]中拓扑的性能指标PI=1.253 3[18],而采用本文的方法得到拓扑PI= 1.275 5。这表明本文的方法得到拓扑结构性能比文献[17]中的优,同时它的计算效率更高。
参数设置如下:优化目标体积比![]() ;体积约束限系数
;体积约束限系数![]() ;阻尼系数
;阻尼系数![]() ;过滤函数系数
;过滤函数系数![]() ;拓扑变量下限值
;拓扑变量下限值![]() (i=1, 2, …, P);拓扑变量变化阀值
(i=1, 2, …, P);拓扑变量变化阀值![]() 。设置单元删除阀值
。设置单元删除阀值 ![]() 初始值为0.01,当优化结构接近约束体积后提高
初始值为0.01,当优化结构接近约束体积后提高![]() 到0.05,单元增加阀值
到0.05,单元增加阀值![]() 为
为![]() 。
。
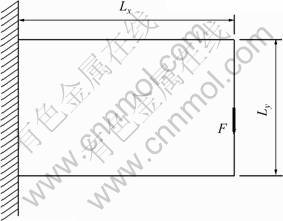
图2 短悬臂梁初始设计区域
Fig.2 Initial design domain for a short cantilever
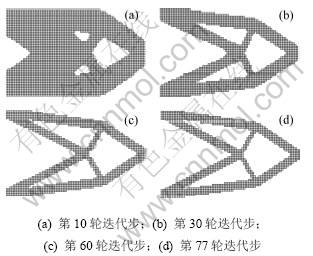
采用本文方法得到的悬臂梁拓扑结构演化历程如图3所示,共进行77轮迭代。图3(a)所示为第10轮迭代后得到的拓扑结构,结构的体积为2.468 8×10-4 mm3,柔顺度为0.072 034 2;图3(b)所示为第30轮迭代后得到的拓扑结构,结构的体积为1.350 4×10-4 mm3,柔顺度为0.136 74;图3(c)所示为第60轮迭代后得到的拓扑结构,结构的体积为1.0×10-4 mm3,柔顺度为0.133 01;图3(d)所示为第77轮迭代后得到的拓扑结构,结构的体积为9.6×10-5 mm3,柔顺度为0.130 37。
图3 本文方法得到的短悬臂梁结构拓扑演化历程
Fig.3 Evolutionary history of a short cantilever structure obtained by proposed method
图4所示为结构达到最优时拓扑变量的分布状态。从图4可以看出:结构只存在少量的低密度单元,最优结构接近完全的0~1分布。

图4 拓扑变量值分布图
Fig.4 Topology variable value distribution diagrams of topology structures
6.2 简支梁结构拓扑优化设计
如图5所示简支梁,一端固定铰支座,另一端为可以横向滚动的铰支座,梁的尺寸是Lx=0.16 m,Ly= 0.03 m,厚度t=0.02 m,在梁的上边缘中部20 mm长的区域铅垂方向施加F=50 kN/m的均布线载荷。弹性模量E=210 GPa,泊松比![]() =0.3,密度为7.8 t/m3。初始设计区域为0.16 m×0.03 m×0.02 m的立体区域,将其划分为128×24×2即6 144个八节点六面体单元网格。
=0.3,密度为7.8 t/m3。初始设计区域为0.16 m×0.03 m×0.02 m的立体区域,将其划分为128×24×2即6 144个八节点六面体单元网格。

图5 简支梁初始设计区域
Fig.5 Initial design domain for a simply supported beam
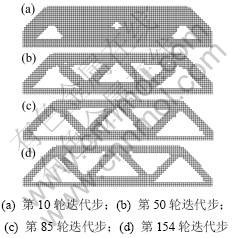
采用本文方法得到的悬臂梁拓扑结构演化历程如图6所示。经过154轮迭代步达到最优拓扑(见图6(d))。
图6 本文方法得到的简支梁结构拓扑演化历程
Fig.6 Evolutionary history of a simply supported beam structure obtained by proposed method
7 结论
(1) 借鉴有理分式材料模型, 建立了结构刚度矩阵与拓扑变量的关系,给出了不影响光滑求解算法收敛特性的设计空间调整策略和手段。
(2) 根据优化准则法,结合变体积约束限措施,提出了一种考虑柔顺度要求和基于设计空间调整的结构拓扑优化方法。
(3) 算例表明该方法能获得较好0~1分布特征的优化拓扑,能解决材料分布和分析计算量大的问题。
参考文献:
[1] Cheng G D, Olhoff N. An investigation eoncerning optimal design of solid elastic plates[J]. International Journal of Solids and Structures, 1981, 17(3): 305-323.
[2] Bendsoe M P, Kikuchi N. Generating optimal topologies in structural design using a homogenization method[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224.
[3] Belblidia F, Lee J E B, Rechak S, et al. Topology optimization of plate structures using a single- or three-layered artificial material model[J]. Advances in Engineering Software, 2001, 32(2): 159-168.
[4] Giuseppe C A. Hierarchical solution of large-scale three- dimensional topology optimization problems[C]//The 1996 ASME Design Engineering Technical and Computer in Engineering Conference Miechigan. Miechigan State University, 1996.
[5] 荣见华, 唐国金, 罗银燕, 等. 考虑位移要求的大型三维连续体结构拓扑优化数值技术研究[J]. 工程力学, 2007, 24(3): 20-27.
RONG Jian-hua, TANG Guo-jin, LUO Yin-yan, et al. A research on the numerical topology optimization technology of large three-dimensional continuum structural considering displacement requirements[J]. Engineering Mechanics, 2007, 24(3): 20-27.
[6] 荣见华, 姜节胜, 胡德文, 等. 基于应力及其灵敏度的结构拓扑渐进优化方法[J]. 力学学报, 2003, 35(5): 584-591.
RONG Jian-hua, JIANG Jie-sheng, HU De-wen. A structural topology evolutionary optimization method based on stresses and their sensitivity[J]. Acta Mechanica Sinica, 2003, 35(5): 584-591.
[7] Wang X, Wang M Y, Guo D. Structural shape and topology optimization in a level-set-based framework of region representation[J]. Structural and Multidisciplinary Optimization, 2004, 27(1/2): 1-19.
[8] 欧阳高飞, 张宪民. 结构拓扑优化中水平集方法的快速初始化研究[J]. 应用基础与工程科学学报, 2008, 16(1): 136-143.
OUYANG Gao-fei, ZHANG Xian-min. Research on fast initialization for the level set method in structural topology optimization[J]. Journal of Basic Science and Engineering, 2008, 16(1): 136-143.
[9] Sui Y K, Yang D Q. A new method for structural topological optimization based on the concept of independent continuous variables and smooth model[J]. Acta Mechanica Sinica, 1998, 18(2): 179-185.
[10] 隋允康, 叶红玲, 刘建信, 等. 追究根基的结构拓扑优化方法[J]. 工程力学, 2008, 25(A02): 7-19.
SUI Yun-kang, YE Hong-ling, LIU Jian-xin, et al. A structural topological optimization method based on exploring conceptual root[J]. Engineering Mechanics, 2008, 25(A02): 7-19.
[11] 郭旭, 赵康. 基于拓扑描述函数的连续体结构拓扑优化方法[J]. 力学学报, 2004, 36(5): 522-526.
GUO Xu, ZHAO Kang. A new topology description function based approach for structural topology optimization[J]. Acta Mechanica Sinica, 2004, 36(5): 522-526.
[12] 程耿东. 工程结构优化设计基础[M]. 北京: 水利电力出版社, 1984: 161-170.
CHENG Geng-dong. The base of optimal design of engineering structure[M]. Beijing: The Publishing Company of Water and Electricity, 1984: 161-170.
[13] Jang I G, Kwak B M. Design space optimization using design space adjustment and refinement[J]. Structural and Multidisciplinary Optimization. 2008, 35(1): 41-54.
[14] Kim I Y, Kwak B M. Design space optimization using a numerical design continuation method[J]. Int J Numer Methods Eng, 2002, 53: 1979-2002.
[15] Stolpe M, Svanberg K. An alternative interpolation scheme for minimum compliance topology optimization[J]. Structural and Multidisciplinary Optimization, 2001, 22(2): 116-124.
[16] Liang Q Q, Steven G P. A performance-based optimization method for topology design of continuum structures with mean compliance constraints[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191(13/14): 1471-1489.
[17] Suzuki K, Kikuchi N. A homogenization method for shape and topology optimization[J]. Computer Methods in Applied Mechanics and Engineering, 1991, 93(3): 291-318.
[18] RONG Jian-hua, LIANG Qing-quan. A level set method for topology optimization of continuum structures with bounded design domains[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(17/18): 1447-1465.
(编辑 陈灿华)
收稿日期:2010-06-28;修回日期:2010-09-02
基金项目:国家自然科学基金资助项目(10472016,10872036);国家高技术研究发展计划(“863”计划)项目(2008AA04Z118);湖南省高等学校科学研究项目(09C074)
通信作者:易继军(1977-),男,湖北钟祥人,博士研究生,从事结构设计与优化;电话:15874980592;E-mail: jijunyi@gmail.com