基于组合进化算法的混沌时间序列重构相空间参数选取-有色金属在线

Abstract: A method of combinative evolutionary algorithm optimized parameters of phase space reconstruction is proposed for predicting chaotic time series. First, it establishes an information entropy optimum mathematical model in phase space for embedding dimension and delay time. It then solves these two parameters with an improved combinative evolutionary algorithm (CEA) simultaneously. The chaotic time series are predicted using least squares support vector machine. The results show that it not only determines two parameters at the same time, but also can improve the performance of chaotic time series prediction.

Key words: chaotic time series; combinative evolutionary algorithm; prediction; information entropy

混沌系统在现实生活中普遍存在，混沌时间序列的分析与预测都是在重构相空间中进行的，因此相空间重构在混沌时间序列分析和预测中有着重要意义。相空间重构方法是由Takens^[1]提出的，其中延迟时间τ和嵌入维数m的正确选取是相空间重构成功的关键所在。目前对2个参数的选取主要有2类方法，一类是认为两者互不相关，即延迟时间τ和嵌入维数m的选取可以独立进行，如文献[2]先采用互信息方法选取延迟时间τ，然后采用伪最近邻域方法确定嵌入维数m。文献[3]则先采用自相关方法选取τ，然后利用G-P方法确定合适的m。另一类方法是认为延迟时间τ和嵌入维数m是相关的，如时间窗口方法^[4]、C-C方法^[5]等，它们明确了延迟时间τ和嵌入维数m具有整体的乘积关系。然而上述方法重构的相空间并不一定最佳，不能很好地保持原动力系统整体的特性。文献[6]验证了在不同延迟时间τ和嵌入维数m选择下，一些典型混沌系统在预测时具有不同的误差，这进一步说明相空间重构参数τ和m是整体相关的。信息熵是系统整体性的一种度量，在复杂系统时间序列尤其是混沌时间序列的分析中具有重要作用。如文献[7-8]分别应用条件熵解决了混沌时间序列的时滞判定和求解嵌入维数m。但是上述2个文献只是孤立讨论了重构参数τ和m与信息熵的关系，没有将2个重构参数τ和m用信息熵模型统一表示出来。文献[9]首先建立延迟时间τ和嵌入维数m的信息熵优化模型，将τ和m作为一个整体，然后利用基本遗传算法对优化模型进行求解，结合Elman网络进行混沌时间序列预测。然而，基本遗传算法具有收敛速度慢、易陷入局部最优等缺点，难以满足混沌时间序列实时预测的目的。此外，神经网络存在过拟合、易陷入局部极小值、网络结构的选择过分依赖于经验等缺陷。进化算法(evolutionary algorithms，EA)是近年发展起来的一种模仿生物进化规律而演化出的全局优化方法，它通过交叉、变异和选择算子不断优化群体，直至收敛于全局最优解^[10]。在过去的几十年中，研究人员对EA中的交叉、变异算子进行了大量的研究，并且提出了许多有益的建议和结论，这些已有的经验和结论对改进进化算法的性能非常有帮助。同时我们还观察到，几乎所有的进化算法在求解优化问题时仅采用单一的交叉算子结合单一的变异算子，这样一来，算法的搜索多样性缺陷就不可避免。基于统计理论的最小二乘支持向量机(LSSVM)是近年来机器学习领域的重要成果之一，其训练过程遵循结构风险最小化原则，结构参数在训练过程中根据样本数据自动确定，不易发生过拟合现象，将支持向量机的学习问题转化为求解线性方程组问题，不存在局部极小值问题，因此，LSSVM可成功克服神经网络的缺陷，在混沌时间序列分析和预测中有广泛的应用^[11-12]。本文作者首先建立延迟时间τ和嵌入维数m在相空间中的信息熵优化模型，使相空间中的重构坐标最大限度独立的同时又保持其动力学关系。然后提出一种改进的组合进化算法求解该信息熵优化模型，扩充了两个重构参数所具有的整体性关系。最后结合最小二乘支持向量机对几个混沌时间序列进行预测，实验结果表明了该方法的有效性。

1 τ和m的信息熵优化模型

1.1 信息熵模型

假设2个随机变量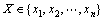和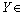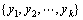，其先验概率分别为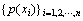和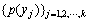。信息熵可定义为^[9]：

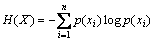(1)

式(1)描述了随机变量X的不定性，即为消除X的不确定性所需要的平均信息量。类似地可以定义联合熵

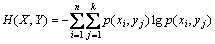(2)

其中：p(x_i，y_j)为联合概率。

根据条件概率p(x_i|y_j)定义条件熵

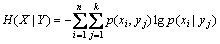(3)

式(3)描述了已知Y后X“残留”的不定性。一般有H(X)≥H(X|Y)，即已知Y后有利于消除X的不定性，特别地H(X|Y)=0表示Y已知后X的不定性完全消除，即Y能够完全确定X。由式(1)，(2)和(3)可以推出

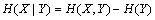(4)

1.2 相空间重构参数τ和m信息熵优化模型

假设混沌系统产生的时间序列为x(1)，x(2)，…，x(n)，…，根据嵌入定理，总存在合适的维数m，时间延迟τ的相空间X(n)=(x(n)，x(n+τ)，…，x(n+(m-1)τ))∈R^m，(n=1，2，…)，使得重构相空间中的“轨线”与原混沌系统在微分同胚意义下是等价的^[9]。即存在一个光滑映射F:R^m→R^m能复原出原混沌系统的“运动过程”，相空间点的轨迹为

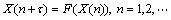(5)

其中：。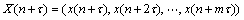

把式(5)表示为分量形式有

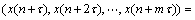
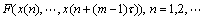(6)

式(6)可进一步化简为时间序列形式

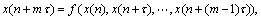
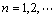(7)

式(7)表明：在合适的时间延迟τ和嵌入维数m选择下，f能反映原系统的“运动形式”。由于混沌系统的复杂性，要具体明确f的解析形式是困难的。下面先讨论f中τ和m所具有的一般熵关系，然后利用最小二乘支持向量机来逼近f。

由于混沌系统具有高度非线性的特点，因此所观测到的时间序列具有确定的随机性，即未来某时刻的值具有不确定性。式(7)说明，在知道x(n)，x(n+τ)，…，x(n+(m-1)τ)后可以恰好确定x(n+mτ)，即在知道特定的m个时刻的值x(n)，x(n+τ)，…，x(n+(m-1)τ)后未来某时刻x(n+mτ)的不确定性完全消除，而在知道其他m个时刻的值或少于m个时刻的值都不能完全消除x(n+mτ)的不确定性。因此，为了消除未来某时刻的不确定性，时间延迟τ和嵌入维数m是紧密联系的。时间序列的不确定性可以用信息熵来刻画，所以可以建立时间延迟τ和嵌入维数m的熵关系。记X₁=x(n)，X₂=x(n+τ)，…，X_m=x(n+(m-1)τ)， X_m₊₁= x(n+mτ)，用H(X_m₊₁)表示x(n+mτ)的不定性，根据条件熵的定义，有H(X_m₊₁|X_m)表示已知X_m后X_m₊₁仍“残留”不定性，因为只知x(n+(m-1)τ)的信息不足以确定x(n+mτ)，显然有H(X_m₊₁|X_m)＞0。以此类推，根据式(7)有

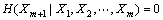(8)

因此，得到求τ和m的优化模型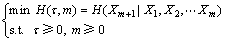^[9]：

(9)

根据式(4)将条件熵转化为联合熵，则

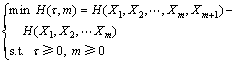(10)

在式(9)或(10)表示的优化问题中，由于目标函数中的熵函数是含时间延迟τ和嵌入维数m的一个很复杂的表达式，传统的基于梯度信息的优化方法很难求解。基于组合进化算法具有收敛速度快、全局寻优能力强的特点，本文提出一种改进的组合进化算法来求解。

2 改进的组合进化算法优化τ和m

2.1 改进的组合进化算法

2.1.1 种群初始化

由进化算法的机理可知，交叉操作对种群的依赖性较强，而进化算法的搜索速度主要依赖于交叉操作。若随机初始化种群个体则不利于搜索问题的全局最优解，可能会导致增加迭代次数来达到近似最优解，这势必会增加了算法的计算量。佳点集方法是一种有效的、可以减少实验次数的实验方法。在相同取点数个数的条件下，佳点序列要比其他方法选取的点序列更均匀^[13]。因此，本文采用佳点集方法产生初始种群，从而保证了种群个体的多样性。图1所示为采用佳点集方法产生的规模为80的初始种群个体分布。

从图1可以看出：与随机方法相比，佳点集方法生成的初始种群个体分布均匀，具有较好的多样性。

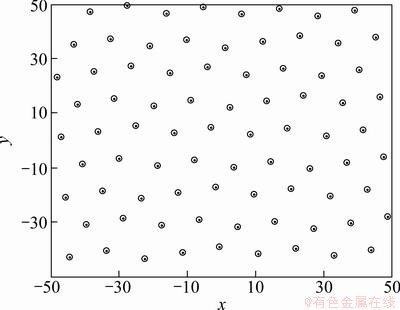
图1 佳点集方法产生的初始群体分布

Fig. 1 Initial individuals with good point set method

2.1.2 组合交叉和变异策略

交叉算子是进化算法搜索整个决策空间的重要操作，它通过组合父代个体的信息形成新的子代个体，是决定进化算法是否收敛的关键。在进化算法中，常用的交叉算子有单点交叉算子、多点交叉算子、单形交叉算子和算术交叉算子等。变异算子也是进化算法的重要操作，它可以避免算法陷入局部最优，同时也能保持种群的多样性。在进化算法中，常用的变异算子有非均匀变异、多样性变异和边界变异等。

在过去的十多年中，进化算法研究人员对其交叉算子和变异算子进行了大量的研究，并且得到了一些定性和定量的结论，例如已经得到哪些交叉算子适合于全局搜索，哪些交叉算子能平衡算法的全局和局部搜索能力，哪些变异操作能加快算法的收敛速度等。这些已有的知识和经验对改进进化算法的性能非常有帮助。然而，在设计进化算法时，它们却没有被系统地利用。另外，在求解不同的优化问题时，到底选取哪种交叉算子结合哪种变异算子，没有什么系统的规律可循，只有不断地进行实验调试，这一过程需要复杂的计算量。同时还观察到，目前大部分进化算法仅采用单一的交叉算子结合单一的变异算子，这样一来，算法在搜索多样性方面的局限将不可避免。一般来说，期望不同的交叉算子结合不同的变异算子具有不同的特征，产生的新个体能保持群体的多样性，利用它们可以相互补充以求解不同类型的优化问题，从而增强了算法的通用性。

基于上述分析，本文提出一种基于知识库的组合进化算法，即首先建立交叉算子知识库和变异算子知识库，在进化过程中从2个知识库中随机组合知识产生若干个新的个体，从而保证种群个体的多样性，其思路可由图2予以解释。

本文采用2组交叉算子，即单形交叉算子^[14]和算术交叉算子与3组变异算子，分别是非均匀变异、多样性变异和边界变异^[15]，也就是图2中的s=2，r=3。

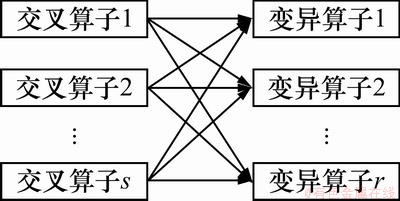
图2 组合交叉算子和变异算子示意图

Fig. 2 Illustration of combining crossover and mutation

上述2组交叉算子和3组变异算子在设计进化算法时频繁使用，它们所具备的特征也已被广泛研究。该组合策略的基本特点是：单形交叉算子和算术交叉算子在关于进化算法的文献中使用最为普遍，因为单形交叉算子在算法初期具有较强的全局搜索能力，而在算法后期具有较强的局部搜索能力；算术交叉算子产生的后代个体一定在2个父代个体之间的连线上，如果接近全局最优解的个体进行交叉操作，对找到全局最优很有帮助。边界变异、非均匀变异和多样性变异在关于进化算法的文献中使用也很普遍。边界变异算子具有很强的局部搜索能力；非均匀变异在进化初期具有较强的全局搜索能力，在进化后期具有较强的局部搜索能力；多样性变异算子具有较强的全局搜索能力。

2.1.3 算法步骤

基于知识库的组合进化算法流程图如图3所示。

2.1.4 数值实验

为验证改进组合进化算法的有效性，选择4个标准测试函数，它们是f₁，f₂，f₃和f₄进行仿真实验。4个函数的具体表达式如下：

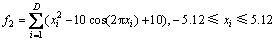
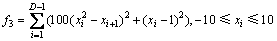
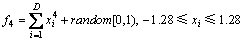
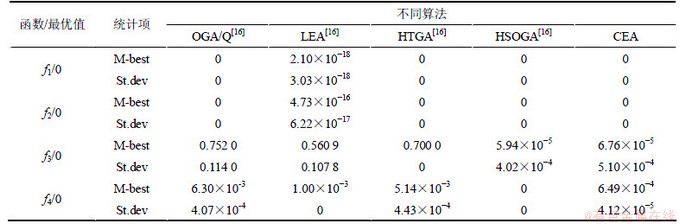
函数f₁，f₂和f₄的维数设置为D=30，f₃的维数为D=100，4个测试函数的全局极小值都为0，函数f₂和f₃为多峰函数，具有多个局部极小点，在搜索过程中易陷入局部最优，这些函数能检验算法的多峰搜索能力。对所有函数，本文算法的参数设置为：种群规模N=200，交叉概率p_c=0.8，变异概率p_m=0.1，最大迭代次数为3 000。其他算法的参数设置见各自文献。对每个函数，在相同的条件下独立运行了30次实验，记录其平均最优值(M-best)和标准差(St.dev)。将本文算法记为CEA，并与其他4种性能较好的算法，即OGA/Q算法^[16]、LEA算法^[16]、HTGA算法^[16]和HSOGA算法^[16]的实验结果进行了比较。表1给出了5种算法对4个函数的寻优结果。

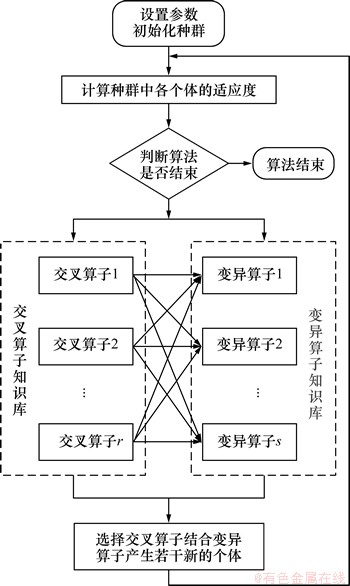
图3 组合进化算法流程图

Fig. 3 Flow chart of combination evolutionary algorithm

从表1可以看出：对于函数f₁和f₂，CEA算法30次实验中一致地找到全局最优解，对于函数f₃和f₄的实验结果也非常接近最优解。与OGA/Q算法相比，CEA算法在函数f₃上得到的结果要优于OGA/Q算法，在函数f₁，f₂和f₄上得到的结果相似。与LEA算法相比，CEA算法在函数f₁，f₂和f₃上得到的结果要优于LEA算法，在函数f₄上得到的结果相似。与HTGA算法相比，CEA算法在函数f₃上得到的结果要优于HTGA算法，在函数f₁，f₂和f₄上的结果两者相当。与HSOGA算法相比，除了函数f₄上得到的结果稍差外，在其他3个函数上得到了相似的结果。基于以上比较分析可以得出：CEA算法具有较强的全局寻优性能，优于或相似于其他算法。

表1 5种算法对4个测试函数的实验结果比较

Table 1 Experimental results of five algorithms on four benchmark functions

2.2 改进的组合进化算法优化τ和m

式(10)所示的信息熵模型中重构参数时间延迟τ和嵌入维数m优化的思想是通过迭代算法搜索一组重构参数(τ，m)，使目标函数达到最小。本文采用前面所描述的改进组合进化算法(CEA)来进行优化时间延迟τ和嵌入维数m，将定义域内一组重构参数序列(τ，m)作为CEA算法中的个体，各个体的适应度函数取式(10)。基于CEA优化信息熵模型重构参数τ和m的具体步骤如下：

Step 1 设置参数，采用佳点集方法初始化种群,每个个体对应于信息熵模型(10)中的一组重构参数 (τ，m)。

Step 2 计算个体的适应度，即直接计算在给定参数τ和m的条件下联合熵|H(X₁，X₂，…，X_m₊₁)-H(X₁，X₂，…，X_m)|作为个体x的适应度。采用矩阵标识法^[8]来计算联合熵H(X₁，X₂，…，X_m)。

Step 3 判断是否满足迭代终止条件，若满足，则迭代结束输出最优时间延迟和嵌入维数(τ，m)；否则继续执行Step 4。

Step 4 组合不同的交叉算子和变异算子产生新的子代个体，然后返回Step 2。

3 实例仿真与分析

为了验证本文方法的有效性，使用最小二乘支持向量机(LSSVM)对混沌时间序列进行预测实验。LSSVM预测模型的核函数类型和参数设置与文献[12]相同。为了评价预测效果引入如下评判标准：

均方误差(MSE)：

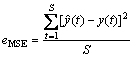(11)

均方根误差(RMSE)：

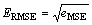(12)

绝对误差(e(t))：

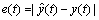(13)

相对误差(e_r(t))：

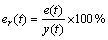(14)

其中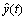：，y(t)和S分别表示预测值、真实值和样本大小。

3.1 预测Lorenz吸引子时间序列

Lorenz吸引子系统的方程为

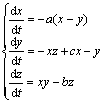(15)

当c≥28时，Lorenz系统(15)处于混沌状态。选取系统参数a=10，b=8/3，c=28，初始值为(0.003 1，0.192 8，0.420 8)，采样时间为0.01 s生成变量x的数据，得到Lorenz系统混沌时间序列如图4所示。

利用前1 500组数据作为训练样本集，进行训练建立LSSVM预测模型，用后1 000组数据作为检验样本集，用来测试LSSVM预测模型的有效性。本文方法中的改进CEA算法参数设置为：种群规模N=20，交叉概率p_c=0.8，变异概率p_m=0.1，最大迭代次数为100，得到最优的重构参数为：嵌入维数m=9，时间延迟τ=4。表2给出了本文方法与文献[9]中的方法对Lorenz时间序列的预测结果比较。

从表2可以看出：本文方法对Lorenz吸引子系统的预测结果明显优于文献中其他方法重构相空间上的预测结果，同时也说明了该方法能得到合适的重构参数，提高了预测精度。图5所示为本文方法的预测误差。从图5可知，本文方法具有较小的预测误差。

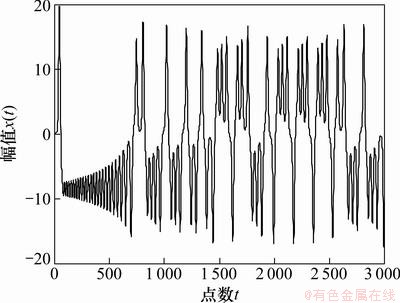
图4 c=28时的Lorenz混沌时间序列

Fig. 4 Lorenz chaos time series with c=28

表2 Lorenz混沌时间序列的预测结果比较

Table 2 Forecasting results of Lorenz chaos time series

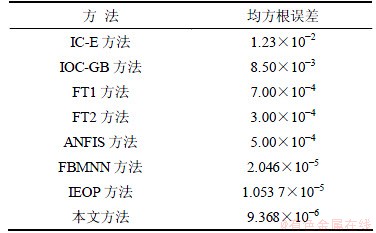
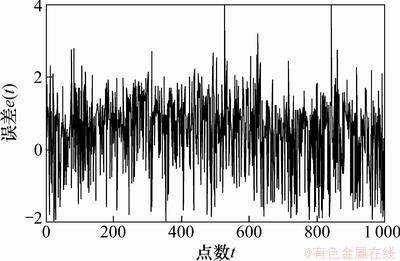
图5 Lorenz混沌时间序列的预测误差

Fig.5 Forecasting error of Lorenz chaos time series

3.2 预测Mackey-Glass时间序列

Mackey-Glass混沌时间序列预测通常被认为是检验和比较各种非线性模型和算法的一个标准测试问题。Mackey-Glass系统为：

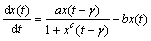(16)

其中：γ为时滞参数，当γ≥17时，系统(16)呈现出混沌性。选取参数a=0.2，b=0.1，c=10，γ=17，初始值x(0)=1.2，步长为h=0.1，采用四阶Runge-Kutta法生成1 000个数据，图6所示为γ=17时的Mackey-Glass混沌时间序列。

把前500组数据作为训练样本集，进行训练建立LSSVM预测模型，后500组数据作为检验样本集，用来测试LSSVM模型的性能。利用第3节中的改进组合进化算法(CEA)优化相空间重构参数，得出m=10和τ=6，即Mackey-Glass系统重构相空间嵌入维数m=10，延迟时间τ=6。

表3给出了本文方法与文献[9]中的方法得到的预测结果比较。从表3可知，对Mackey-Glass数据进行预测，本文方法得到的结果要比文献中其他方法得到的结果要优。图7给出了本文方法的预测误差。从图7可以看出，本文方法具有较高的预测精度。

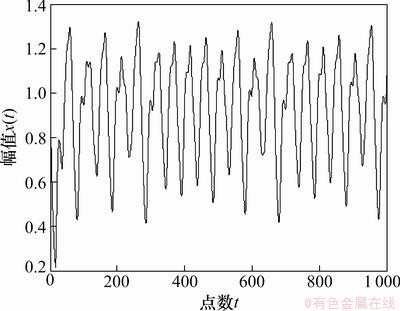
图6 τ=17时的Mackey-Glass混沌时间序列

Fig. 6 Mackey-Glass chaos time series with τ=17

表3 Mackey-Glass时间序列的预测结果比较

Table 3 Forecasting results of Mackey-Glass time series

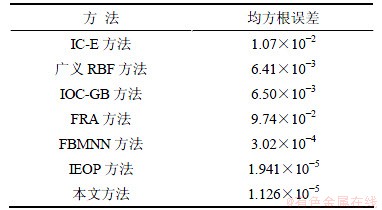
图7 Mackey-Glass混沌时间序列的预测误差

Fig. 7 Forecasting error of Mackey-Class chaos time series

3.3 预测加拿大山猫时间序列

加拿大山猫时间序列是Mackezie河流域每年捕获的加拿大山猫数量，它在一定程度上反映了Mackezie河流域山猫种群的大小。因此，对它进行预测有利于这一区域系统种群动态的研究。这组时间序列数据共有114个，对应的年份为1821—1934年，其被广泛用来测试非线性模型的预测能力^[13]。对114个数据取基为10的对数后所构成的时间序列如图8所示。

将前100个数据作为训练样本集，用来训练建立LSSVM预测模型，后12个数据作为检验样本集，用来测试LSSVM模型的性能。利用第3节中的改进组合进化算法(CEA)优化相空间重构参数，得出m=8和τ=3，即加拿大山猫时间序列重构相空间嵌入维数m=8，延迟时间τ=3。

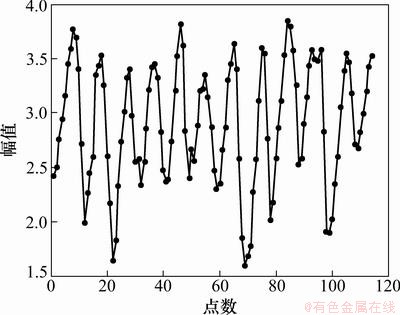
图8 加拿大山猫数据(log₁₀尺度)时间序列

Fig. 8 Canada lynx data time series

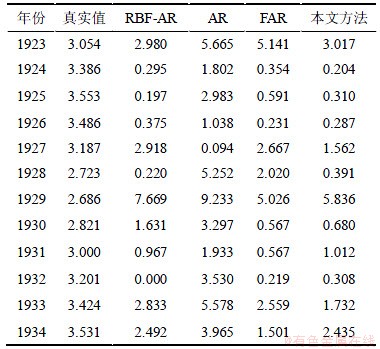
表4给出了本文方法与RBFAR方法^[13]、AR方法^[13]和FAR方法^[13]对加拿大山猫时间序列的预测结果比较，表4中的结果以相对误差的形式给出。从表4可知，与文献中其他方法相比，本文方法具有较高的预测精度。

表4 加拿大山猫时间序列的预测结果比较

Table 4 Forecasting results of Canada lynx time series %

4 结论

(1) 鉴于时间延迟τ和嵌入维数m的整体相关性，利用信息熵知识建立了τ和m的信息熵优化模型。

(2) 提出一种组合进化算法来求解信息熵优化模型，通过建立交叉算子和变异算子知识库，组合知识以产生新的个体，增强算法的全局搜索能力。

(3) 该方法无需知道混沌时间序列的解析模型，只需要其历史数据，采用LSSVM进行训练建立混沌时间序列的预测模型，可以实现很好的预测。

参考文献：

[1] Takens F. Dynamical systems and turbulence[M]. Berlin: Springer-Verlag Press, 1981: 366-381.

[2] Fraser A M. Information and entropy in strange attractors[J]. IEEE Transactions on Information Theory, 1989, 35(2): 245-262.

[3] Albano A M, Muench J, Schwartz C, et al. Singular-value decomposition and the grassberger-procaccia algorithm[J]. Physical Review A, 1988, 38(6): 3017-3026.

[4] Kugiumtzis D. State space reconstruction parameters in the analysis of chaotic time series-the role of the time window length[J]. Physica D, 1996, 95(1): 13-28.

[5] Kim H S, Eykholt R, Salas J D. Nonlinear dynamics delay times and embedding windows[J]. Physica D, 1999, 127(1): 48-60.

[6] Ataei M, Lohmann B, Khaki-sedigh A, et al. Model based method for estimating an attractor dimension from uni/multi- variate chaotic time series with application to Bremen climatic dynamics[J]. Chaos, Solitons and Fractals, 2004, 19(5): 1131-1139.

[7] 田玉楚. 混沌时间序列的时滞判定[J]. 物理学报, 1997, 46(3): 442-447.

TIAN Yuchu. Delay indentification in chaotic time series[J]. Acta Physica Sinica, 1997, 46(3): 442-447.

[8] 肖方红, 阎桂荣, 韩宇航. 混沌时序相空间重构参数确定的信息论方法[J]. 物理学报, 2005, 54(2): 550-556.

XIAO Fanghong, YAN Guirong, HAN Yuhang. Information theory approach to determine embedding parameters for phase space reconstruction of chaotic time series[J]. Acta Physica Sinica, 2005, 54(2): 550-556.

[9] 马千里, 彭宏, 张春涛. 基于信息熵优化相空间重构参数的混沌时间序列预测[J]. 物理学报, 2010, 59(11): 7623-7629.

MA Qianli, PENG Hong, ZHANG Chuntao. Chaotic time series prediction based on information entropy optimized parameters of phase space reconstruction[J]. Acta Physica Sinica, 2010, 59(11): 7623-7629.

[10] Wang Y P, Dang C Y. An evolutionary algorithm for global optimization based on level-set evolution and Latin squares[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(5): 579-595.

[11] Suykens J A K, Vandewalle J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300.

[12] 龙文, 梁昔明, 龙祖强, 等. 基于改进蚁群算法优化参数的LSSVM短期负荷预测[J]. 中南大学学报, 2011, 42(11): 3408-3414.

LONG Wen, LIANG Ximing, LONG Zuqiang, et al. Parameter selection for LSSVM based on modified ant colony optimization in short-term load forecasting[J]. Journal of Central South University, 2011, 42(11): 3408-3414.

[13] 龙文. 求解两类优化问题的混合进化算法及其应用[D]. 长沙: 中南大学信息科学与工程学院, 2011: 56-58.

LONG Wen. Hybrid evolutionary algorithms for solving two classes optimization problems and applications[D]. Changsha: Central South University. School of Information Science and Engineering, 2011: 56-58.

[14] Wang Y, Cai Z X, Zhou Y R, et al. Constrained optimization based on hybrid evolutionary algorithm and adaptive constraint- handling technique[J]. Structural and Multidisciplinary Optimization, 2009, 37(4): 395-413.

[15] 梁昔明, 龙文, 秦浩宇, 等. 基于种群个体可行性的约束优化进化算法[J]. 控制与决策, 2010, 25(8): 1129-1132.

LIANG Ximing, LONG Wen, QIN Haoyu, et al. Constrained optimization evolutionary algorithm based on individual feasibility of population[J]. Control and Decision, 2010, 25(8): 1129-1132.

[16] 江中央, 蔡自兴, 王勇, 等. 求解全局优化问题的混合自适应正交遗传算法[J]. 软件学报, 2010, 21(6): 1296-1307.

ZHANG Zhongyang, CAI Zixing, WANG Yong, et al. Hybrid self-adaptive oxthogonal genetic algorithm for solving global optimization problems[J]. Journal of Software, 2010, 21(6): 1296-1307.

(编辑陈爱华)

收稿日期：2012-10-04；修回日期：2012-12-20

基金项目：贵州省科学技术基金资助项目(黔科合J字[2013]2082号)；贵州省教育厅125重大科技专项项目(黔教合重大专项字[2012]011号)

通信作者：龙文(1977-)，男，湖南隆回人，博士，讲师，从事建模与智能优化研究；电话：13639086822；E-mail：lw084601012@gmail.com

摘要：研究一种基于组合进化算法优化相空间重构参数的混沌时间序列预测方法。该方法首先建立时间延迟τ和嵌入维数m在相空间中的信息熵优化模型，然后提出一种改进的组合进化算法同时求解2个重构参数τ和m，结合最小二乘向量机进行混沌时间序列预测。实验结果表明，该方法能够确定合适的相空间重构参数τ和m，提高预测精度。