Development of initial conditions based on attraction of simplest walking model
AN Kang(安康), CHEN Qi-jun(陈启军)
(College of Electronics and Information Engineeing, Tongji University, Shanghai 201804, China)
Abstract: Passive dynamic walking is important for the development of bipedal walking robots. A robust walking model would have a large basin of attraction and require few steps to reach the fixed point. The development of the initial conditions in the basin of attraction of the simplest walking model was discussed. The results show that starting with the initial conditions inside some stripes in the basin of attraction, the model needs fewer steps to approach the periodic fixed point. All paths started with the initial conditions inside the basin of attraction will either pass through a stripe of the region around the fixed point or start within this region.
Key words: passive dynamic walking; attraction basic; biped robots
CLC number: TP242.6 Document code: A Article ID: 1672-7207(2011)S1-0584-05
1 Introduction
Biped walking has an important role in the study of robot motion. Many sophisticated biped prototypes have been built by several important research institutes and companies over the last decades for the understanding of human’s motion. Human’s motion might be a passive dynamic process. McGeer[1-2] introduced his idea of passive dynamic walking, that a biped machine with no actuator and no control could walk stably on a shallow slope. He indicated that human walking is like an unactuate double pendulum where the swing leg is powered only by gravity.
Passive dynamic walking is a periodic walking motion. Garcia et al[3-4] introduced the simplest passive dynamic walking model with stable periodic gait. Schwab et al[5-6] investigated the relationship between the stability and the basin of attraction of the simplest walking model. Hobbelen et al[7] further studied this walking motion by stating that achieving stable periodic gait is possible without locally stabilizing the walking trajectory at every instant in time. However, there is still a problem that these models are sensitive with even a small disturbance. This means that the size of allowable disturbances and the development of these disturbances are important for the stability of the periodic walking motion. In this paper, the development of the initial conditions in the basin of attraction is focused on knowing more about the stability of the periodic passive walking motion.
2 Walking model
The walking model used in this paper is the simplest walking model, which was conceived by Garcia et al[3]. Fig.1 shows the walking model can perform a periodic walking motion on a shallow slope γ using gravity g. The model has two rigid legs with length l, connected by a frictionless hinge at the hip. The mass of this model is only distributed over the hip and two feet. By making the foot mass m much smaller than the hip mass M (m＜＜ M), the influence of the swing foot is negligible in the motion of the model.
Fig.1 Typical passive walking step
The walking step begins at the instant that the two legs are both on the slope. Just after the stance foot hits the slope at heelstrike, and the swing foot is away from the ground. Here there is an assumption that the collision at heelstrike is a no-bounce process and the double support occurs instantaneously. The stance foot acts as a hinge while the swing foot swings freely until the swing foot makes contact with the slope again. Then a new step begins. During the step, the swing foot will briefly be below the floor level when the stance leg is near vertical which explains the inevitable scuffing problem of straight legged walkers. In physical models, knees or powered ankles, 3D motion, or leg shortening measures would solve the problem, but the complexity of the model would increase.
3 Analysis of model
3.1 Equations of motion for swing phase
A global vector X=(xstf, ystf, xhip, yhip, xswf, yswf) which defines the coordinates of the hip and two feet (stance foot and swing foot) describes the whole configuration of the walking model. Define (0, 0) is the coordinate of the contact point of the stance foot in the fixed orthogonal system of coordinates with Ox along the walking slope and Oy directed upward. θ is the angle of the stance leg with respect to Oy, φ is the clockwise angle between the stance leg and the swing leg. The whole configuration of the walking model can also be described by the generalized coordinates q=(θ, φ), the transfer function F between X and q is:
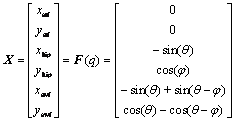(1)
The equations of motion are given below, where β= m/M and θ, φ are functions of time t.
(2)
The simplest walking model where the ‘foot’ is much smaller than the ‘leg’ was studied. Setting β=0 and rescaling time by 
Eq.(3) can be yielded:
(3)
3.2 Heelstrike
When the swing foot hits the ground at heelstrike, the geometric collision condition is
φ-2θ=0 (4)
Here it is assumed that the collision at heelstrike is a fully inelastic impact and the double stance occurs instantaneously. The angular momentum is conserved through the collision at heelstrike. The equation of the angular momentum conservation relations is given below, where the ‘+’ means ‘just after the impact’, and the ‘-’ means ‘just before the impact’:
(5)
From Eq.(5), it is known that although the walking system has four independent initial conditions 
only 
at the start of the step determine the next step. The mapping from one step to the next is 
When it starts with 
which is the initial conditions at the beginning of the step n, the equations of motion (3) will be used until heelstrike occurs. Then Eq.(5) will be used to calculate the initial conditions of the next step 
4 Analysis of model
In this walking model, as mentioned above, are the only independent parameters. So we try to find the period-one gait that started with the initial conditions 
which equals 
, where 
is the initial conditions at the fixed point. After a few steps, when the step number is greater than n (n>i), it will return to the same initial conditions as the last step just after the heelstrike:
The initial conditions can be described by a linearization of the mapping function:
(6)
where 
The eigenvalues of the Jacobian J can determine the stability of the periodic gait. If both eigenvalues are within the unit circle, then the periodic gait is stable and there is a region of initial conditions surrounding the periodic solution that converge to it. This region is called the basin of attraction. If one or both eigenvalues are outside the unit circle, then the gait is unstable.
From Garcia, it is known that there is a stable period-one walking gait for slopes less than about 0.015 rad. Fig.2 shows |λ|max, the maximum of the eigenvalues of J, versus the slope angle γ. If the maximum of the eigenvalues of J is less than 1, the stable period-one gait can be found.
Fig.2 Maximum of eigenvalues of J versus slope angle γ
5 Results
All the initial conditions inside the basin of attraction will lead to a periodic gait. The sequence of the initial conditions spirals towards the fixed point.
5.1 Basin of attraction
Fig.3 shows the basin of attraction with the number of steps starting with the initial conditions to the fixed point. Because the basin of attraction of this model is a very small and thin region, the vertical axis was changed to represent the sum of the stance leg angle θ and scaled angular velocity 
so, the shape becomes better[5]. The fixed point in this picture is (0.200 3, 0.000 5) at a slope of γ=0.009 rad. The colors in the basin of attraction signify the speed of convergence to the fixed point from the initial conditions. The lighter the color is, the more steps the model takes to reach the fixed point. For example, starting from point A, after 11 steps, the initial condition will converge to the fixed point. In this model, the radius of the converging region was set around the fixed point to 0.5%θ. If the initial condition is in this region, it is considered to converge to the fixed point. It is can also be seen that there are some dark stripes in the light region of the basin of attraction. It needs fewer steps for the initial conditions in the dark stripes to converge to the fixed point than the points close to the fixed point. Formerly it was expected that the points close to the fixed point would generally converge faster than points far away. However, it can be seen that some points far away can converge faster than points close to the fixed point. The average number of steps of the initial conditions inside the basin of attraction converge to the fixed point is 12.
If started inside region F, the walker will take a few steps but eventually fall forwards. If started inside region B, the initial conditions will lead it to fall backwards. The farther away the initial condition from the basin of attraction, the smaller the number of successful steps before falling down.
Fig.3 Basin of attraction shaded according to number of steps to reach fixed point (*)
5.2 Development of initial conditions
The left side of Fig.4 shows the paths from the initial conditions towards the fixed point. Every turning point is an initial condition. If started with any initial condition inside the basin of attraction, there will be a sequence of steps spiraling counterclockwise towards the periodic fixed point. We separate the basin of attraction into three parts with two lines that pass through the stable periodic fixed point and the unstable periodic fixed point respectively (see Fig.5). Here, the unstable fixed point is another periodic solution found by our numerical simulation. The eigenvalues of the Jacobian J of this fixed point are outside of the unit circle. So, the initial condition of this fixed point is unstable. The solution of this unstable fixed point is (0.193 9 - 0.01). The initial conditions inside region 1 move towards the lower left region of region 2 (see Figs.4(a) and (b)). The next steps of all the initial conditions inside region 1 will be in region 2. When started with the initial conditions from region 3, the walker will take a few steps then go into the upper right region of region 2 (see Figs.4(c) and (d)). Therefore, all paths started with the initial conditions inside the basin of attraction will either pass through region 2 or start within the region. After the initial conditions get into region 2, the paths spiral towards the periodic fixed point.
The right side of Fig.4 shows the respective motion trajectories of the legs. The walker is started with the initial conditions inside the basin of attraction. After a few steps, the walker is close to the periodic fixed point.
Fig.4 Paths from some initial conditions to fixed point (a, (b), (c), (d)) and motion trajectories of two legs ((a′), (b′), (c′), (d′))
Fig.5 Three regions in basin of attraction (Functions of two lines are y-0.2x+0.039 6=0; y-0.375x+0.083=0)
6 Conclusions
(1) The initial conditions inside the basin of attraction lead to a periodic motion. The sequence of the initial conditions is like a spiral towards the periodic fixed point. If started with the initial conditions out of the basin of attraction, the walker will fall down eventually.
(2) There are some dark stripes in the light region of the basin of attraction. If started with the initial conditions in the dark stripes, it will take fewer steps to approach the periodic fixed point.
(3) The basin of attraction is separated into three parts. All paths started with the initial conditions inside the basin of attraction will either pass through a stripe of the region around the fixed point or start within this region.
(4) A robust walking model would have a large basin of attraction and require few steps to reach the fixed point. Therefore, understanding the properties of the basin of attraction is very helpful for designing a robust walking model. This is the reason why we intend to continue research on the basin of attraction, and try to find a solution to improve the performance of the basin of attraction.
References
[1] McGeer T. Passive dynamic walking[J]. International Journal of Robotics Research, 1990, 9(2): 62-82.
[2] McGeer T. Passive walking with knees[C]//Proceedings of the IEEE International Conference on Robotics and Automation, Los Alamos, California, IEEE Computer Society, 1990: 1640-1645.
[3] Garcia M, Chatterjee A, Ruina A, et al. The simplest walking model: Stability, complexity, and scaling[J]. ASME Journal of Biomechanical Engineering, 1998, 20(2): 281-288.
[4] Garcia M, Chatterjee A, Ruina A. Speed, efficiency, and stability of small-slope 2d passive-dynamic bipedal walking[C]//Proc IEEE Int Conf Robotics and Automation, Piscataway, NJ, 1998: 2351-2356.
[5] Schwab A L, Wisse M. Basin of attraction of the simplest walking model[C]//Proceedings of DETC’01, ASME 2001, Pittsburgh, Pennsylvania, 2001: 9-12.
[6] Wisse M, Schwab A L, Linde R Q, et al. How to keep from falling forward: elementary swing leg action for passive dynamic walkers[J]. IEEE Trans On Robotics, 2005, 21(3): 393-401.
[7] Hobbelen D E G, Wisse M. Controlling the walking speed in limit cycle walking[J]. International Journal of Robotics, 2008, 27(3): 989-1005.
(Edited by LONG Huai-zhong)
Received date: 2011-04-15; Accepted date: 2011-06-15
Foundation item: Project(2009AA04Z213) supported by the National High-Tech Research and Development Program of China; Project(2010DFA2210) supported by the International Technology Cooperation Program; Project(10GG11) supported by Shanghai Shuguang Program, China; Project(XD1404800) supported by Shanghai Technical Personnel Program
Corresponding author: CHEN Qi-jun; Tel: +86-13651751103; E-mail: gjchen@mail.tongji.edu.cn
