J. Cent. South Univ. Technol. (2010) 17: 1327-1335

DOI: 10.1007/s11771-010-0638-6

Effects of interface slip and semi-rigid joint on elastic seismic response of steel-concrete composite frames

QI Jing-jing(戚菁菁), JIANG Li-zhong(蒋丽忠)

School of Civil and Architectural Engineering, Central South University, Changsha 410075, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Key words:

composite frame; interface slip; semi-rigid joint; dynamic characteristic; shearing stiffness; rotation stiffness; seismic response；

1 Introduction

In recent years, there have been many fierce earthquakes all over the world that bring about a lot of losses of people’s life and property. The main reason causing casualties is the collapse of buildings. Therefore, studying the seismic behavior of structure systems becomes imperative. Composite frames are widely used in practical engineering because of their small cross section, light mass and high bearing capacity as well as excellent earthquake resistance. Since 1980s, the researchers abroad have studied the seismic behavior of composite frame structures. ELGHAZOULI et al [1] analyzed the influence of key parameters, related to the structural configurations and design loads, on the inelastic seismic behavior of composite frame. LEON [2] proposed a rational, mechanistic approach to the design and analysis of partially restrained frames for seismic loads. PILUSO et al [3] assessed the seismic reliability of a 3D steel-concrete composite building, taking into account both randomness and uncertainty. However, the composite frame systems still belong to a new research and development field at home. Only a few researchers conducted some theoretical and experimental studies on the seismic behavior of composite frame. JIANG et al [4-5] studied the elastic-plasticity seismic responses of composite frames and presented the simplified restoring force model for composite structure; ZONG et al [6] and SHI et al [7] conducted experimental investigations on seismic performances of composite frames.

However, the influences of joint types and interface slip on seismic responses of composite frames were not systematically studied. As for joint types, a lot of research results demonstrate that the semi-rigid joint has great effects on basic mechanic behavior and stability as well as seismic behavior of steel frame [8-11]. Compared with steel frame, composite frames can enhance rigidity and stability as well as better ductility and dissipation energy. But the semi-rigid joint reduces the integral stiffness of composite frame to a certain extent. And the stiffness change will influence the dynamic behavior of composite frame directly. Because of the lack of research literatures about effects of semi-rigid joint on seismic response of composite frame, the mechanic property and failure mechanism are not fully understood. As far as the interface slip is concerned, the investigators at home and abroad conducted deep research on interface slip effects of composite components [12-14], but the influences of interface slip on seismic response of composite frame were not systematically studied. For this reason, further research and application of composite frames are affected. So far, since there have been no special codes for composite structure design in China, the designers have to refer to other related codes, which lead to uneconomic and unreasonable design. Therefore, in order to reduce seismic hazards, it is essential to analyze the seismic responses of semi-rigid joint composite frame considering interface slip and propose strategies and advices for seismic design of composite frame.

In this work, on the basis of finite element model of partial composite beams [15], the element stiffness matrix of semi-rigid joint composite frame in partial connection was derived. Through developing MATLAB program, the dynamic analysis of semi-rigid composite frames considering interface slip was conducted. Introducing two non-dimensional coefficients related to connector shearing rigidity and joint rotational stiffness, the effects of interface slip and semi-rigid joint were transferred to quantitative parametric analysis. The influences of interface slip and semi-rigid joint on dynamic characteristics and elastic seismic responses of composite frame were studied.

2 Element stiffness matrix of composite frame considering interface slip and semi- rigid joint

When dynamic analysis of frame structure is conducted, there will be some common calculation models such as layer model, member system model, and member system-layer model. Because the member system model can well analyze structure stress and damage state, it becomes the ideal choice for structure dynamic analysis. The key of adopting member system model is to establish the element stiffness matrix of beam-column elements. In order to derive the element stiffness matrix of semi-rigid joint composite frame beam in partial connection (see Fig.1), the following assumptions are made.

(1) Both of steel and concrete materials are in elastic stage. Before cracking, the tension and the compression elastic modulus of concrete are equal.

(2) The shear connector between steel beam and concrete slab is in elastic stage, and the shearing force of single connector (Q) and the interface slip between steel beam and concrete slab (s) satisfy equation Q=Ks, where K is the shear stiffness of connector.

(3) Allowing for the enough deformability of flexible connectors, the action of shear connectors is assumed to be uniformly distributed along the beam length.

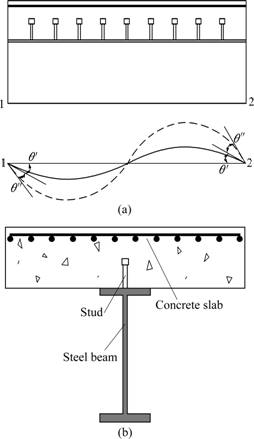
Fig.1 Schematic diagrams of composite beam (andare relative rotation angles of beam and column at both ends, respectively): (a) Semi-rigidly connected composite frame beam element; (b) Cross-section of composite beam

(4) After the deformation of composite beam, the cross-sections of steel beam and concrete slab remain plane.

(5) No matter what loads the composite beam is subjected to, the deflections of steel beam and concrete slab remain the same at any position, namely ignoring the vertical separation between concrete slab and steel beam.

(6) The effects of shearing deformation are not considered.

Based on finite element model of partial composite beam derived by LI and ZHAO [15], the force- displacement relation equation is obtained:

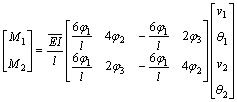        (1)

where M₁ and M₂ are the bending moments of the beam end; θ₁ and θ₂ are the angles of rotation because of bending; v₁ and v₂ are the deflections of beam end. Subscripts 1 and 2 are related to the first and second beam end, respectively; l is the length of the composite beam;

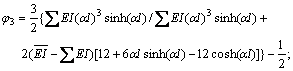
and α comes from Newmark theory

and is the nondimensional parameter related to materials, section physical dimensions and shear stiffness of contact surface; k is the shear modulus of the interface between concrete slab and steel beam, k=K/d, d is spacing interval between studs;  is the elastic flexural rigidity of composite beam section considering fully combined action of concrete slab and steel beam;  is the assembled extensional stiffness of composite beam section;  is the elastic flexural rigidity of composite beam section without combined action of concrete slab and steel beam.

The rotational angles of both ends considering semi-rigid joint are expressed as  and , as shown in Fig.1,

                            (2)

The relationship between moment and rotation angle at a joint is

                        (3)

where K₁ and K₂ are the joint rotation stiffnesses of ends 1 and 2, respectively.

According to Eqs.(1) and (3), we have

(4)

Eq.(4) is simplified as

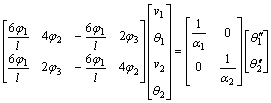   (5)

Introducing   and

γ₁ and γ₂ are the non-dimensional parameters related to the ratio of joint rotation stiffness to beam linear stiffness.

Substituting Eq.(2) into Eq.(5), the relationship between relative rotation angle and displacement is obtained:

(6)

where

;

;

;

.

In order to simplify Eq.(6), some parameters are assumed:

Then, there exists

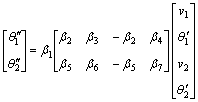             (7)

Substituting Eq.(7) into Eq.(3), we have

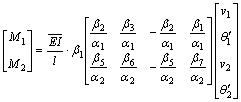       (8)

According to finite element model of partial composite beam derived by LI and ZHAO [15], there exists

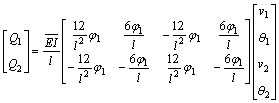 (9)

Substituting Eqs.(2) and (7) into Eq.(9) yields:

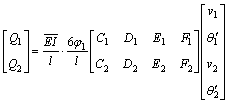        (10)

where Q₁ and Q₂ are the shearing forces of beam ends;

Integrating Eqs.(8) and (10), the element stiffness matrix of composite frame beam considering interface slip and semi-rigid joint is

(11)

where

Therefore, the element stiffness matrix of composite frame beam is symmetrical.

As for element stiffness matrix of composite frame column, the element stiffness matrix of one-way flexural column in Ref.[16] is used:

k_ce=

(12)

whereandare calculated according to Ref.[16].

3 Free vibration characteristics of composite frame structure considering interface slip and semi-rigid joint

The free vibration equation of composite frame system ignoring damping force is

                           (13)

where M is the consistent mass matrix; and K is the global stiffness matrix composed of element stiffness matrixes according to traditional finite element method.

The free vibration without considering damping force is harmonic vibration, namely

                          (14)

where is the eigenvector; and is the angular velocity.

Substituting Eq.(14) into Eq.(13) and eliminating the non-zero itemyield

                               (15)

whereis the eigenvalue.

Eq.(15) is the system of homogeneous algebraic equation. Therefore, the free vibration frequency of composite frame is transferred to a generalized eigenvalue problem. In this work, the subspace iteration method was used to solve the generalized eigenvalue problem. Through developing MATLAB program, the free vibration frequencies were calculated and the mode diagrams were drawn.

In order to analyze the influences of interface slip and semi-rigid joint on free vibration characteristic of composite frame, a two-span six-floor composite frame was considered. The composite frame is made of steel-concrete composite beams and steel columns, the floor is 3 m in height, and the span is 6 m in length. The section of steel column is 200 mm×200 mm×12 mm ×8 mm (Height×Width×Flange thickness×Web thick-

ness), and the section of steel beam in composite beam is 300 mm×150 mm×10 mm×6 mm (Height×Width× Flange thickness×Web thickness). The concrete slab is  1 200 mm in width and 140 mm in length. The material of steel is Q235. The joint connection style is shown in Fig.2 and structural features are found in Ref.[17]. The initial rotational stiffness is 1.263×10¹⁰ N?mm/rad. All the joints have the same initial rotational stiffness, so  is obtained.

The mode analysis of composite frame was conducted by developing MATLAB program. Moreover, the free vibration frequencies of composite frames with different joint types were calculated by taking account of interface slip, and compared with that in Ref.[18]. The first six frequencies of composite frame system considering different factors are listed in Table 1. Known from Table 1, the interface slip and semi-rigid joint reduce the free vibration frequencies of composite beams obviously. The semi-rigid joint has great effects on lower frequencies of composite beam. As for higher frequencies, whether semi-rigid joint is considered or  not, there is not a great difference. When the interface slip and semi-rigid joint are both taken into account, the frequencies are in good agreement with finite element analysis results. Therefore, the above element stiffness matrix of composite beam considering interface slip and semi-rigid joint can analyze composite beam accurately.

The first four modes of composite frame system are shown in Fig.3. These modes are in agreement with those in Ref.[18].

In order to analyze the influences of interface slip and semi-rigid joint on dynamic behavior of composite frame system quantitatively, two non-dimensional parameters α and γ are introduced. An array of various α (α=1, 3, 5, 15, ∞) is assumed to reflect the change of shear connection degree of composite beam. Parameter γ responds to the connection degree of joints through the ratio of joint rotational stiffness to beam linear stiffness. In Eurocodes 3 and 4, the frame joints are divided into hinge joint, semi-rigid joint and rigid joint through varying γ from 0 to ∞. The frequencies changing with α and γ are shown in Fig.4.

As shown in Fig.4, the trends of frequencies in different orders changing with α and γ are in substantial agreement. When α＜5, all frequencies increase to a certain degree with the increment of α; when α＞5, the frequencies do not have significant change with the change of α. It is shown that the interface slip influences the free vibration frequencies of composite frame beam within a certain range. It is known from Fig.4 that all frequencies increase obviously as γ grows when γ＜10, and the amplification of frequencies reduces significantly when γ＞10. As γ＞50, the curves become fairly flat and the frequencies remain basically unchanged. It is implied that when γ is relatively small, the increment of semi-rigid connected degree of joint will decrease the free vibration frequencies of composite frame. However, along with the increment of joint rotational stiffness, the frequency amplifications become smaller.

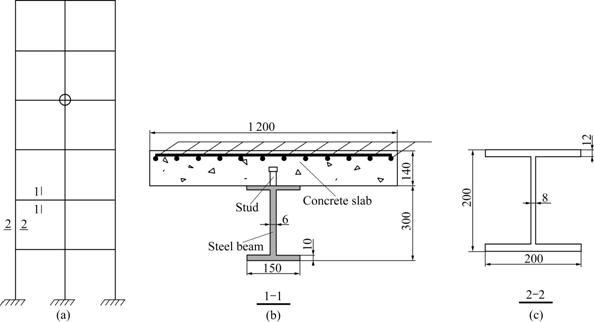
Fig.2 Diagram of calculation example (Unit: mm): (a) Composite frame; (b) Cross-section of steel-concrete composite beam;      (c) Cross-section of steel column

Table 1 Comparison of free vibration frequencies of steel-concrete composite frame (ω: rad/s)

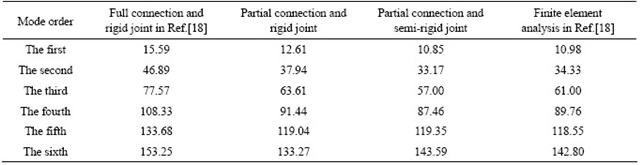
Fig.3 Vibration modes of composite frame system: (a) The first mode; (b) The second mode; (c) The third mode; (d) The fourth mode

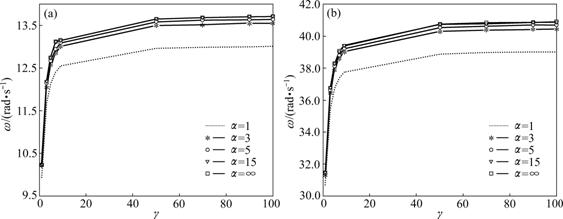
Fig.4 Frequencies of composite frame varying with α and γ: (a) The first order; (b) The second order

The distribution range of the composite frame frequency interval becomes wide with the reduction of joint rotational stiffness and shear connection degree, namely, the free vibration period interval range broadens. It is suggested that the maximum response of composite frame can be obtained in different sections of seismic excitation. In that case, it is highly possible for composite frame to resonate under seismic loads, which is unfavorable to composite frame system. Therefore, the characteristics analyzed above have considerably practical significance for composite frame design.

4 Elastic seismic response analysis of composite frame structure considering interface slip and semi-rigid joint

The differential motion equation of structures subjected to seismic loads is:

               (16)

where M, C, and K are respectively the mass matrix, damping matrix and stiffness matrix of multi-degree of freedom system. Damping matrix C adopts Rayleigh damping matrix. In order to solve the above equation, Wilson-θ method was used. When θ＞1.366, the method is unconditionally stable, so in this work, assume θ= 1.400.

In this work, the seismic analysis of plane composite frame in previous section was conducted. The selected earthquake wave is EI Centro wave whose peak acceleration is 3.41 m/s². The first- and second-order mode damping ratios are ξ₁=0.05 and ξ₂=0.07, respectively. Through developing MATLAB program, the elastic seismic responses of semi-rigid joint composite frame considering interface slip were calculated. The horizontal floor displacements of composite frame under seismic loads considering the interface slip and semi-rigid joint are shown in Figs.5 and 6, respectively.

The elastic time history analysis of composite frame subjected to seismic loads taking interface slip into account is depicted in Fig.5. It is observed that the floor displacements of composite frame considering interface slip are slightly larger than those ignoring interface slip. The time history curves of both are fundamentally coincident, and the effects of interface slip on floors have the same trend.

As shown in Fig.6, when considering semi-rigid joint, the elastic seismic response peak value of composite frame system is distinctly greater than that of rigid composite frame. The distinction is more obvious over time, especially in later vibration. The higher the floor, the greater the distinction. Because the semi-rigid joints reduce the global stiffness of composite frame, the horizontal displacement of composite frame increases. Upon completion of the above analysis, it is essential to consider the influences of semi-rigid joint when the seismic response of composite frame is analyzed, otherwise, the calculation results are unsafe.

The parameter analysis of elastic seismic response of composite frame considering interface slip and semi-rigid joint is demonstrated in Fig.7. When γ＜5, with the increase of γ, the horizontal displacements of floors increase obviously. It is concluded that the increase of joint rotational stiffness increases the horizontal displacement of composite frame. In this range, α has no significant influence on horizontal displacement, which means that the interface slip has nearly no effect on it. When γ＞5, along with the increase of γ and α, the displacement decreases distinctly. After γ and α increase to a certain degree (namely γ＞50 and α＞5), the displacement has no evident change. But with the increment of floors, the effect of γ is greater. When γ=5, the horizontal displacements reach the maximum value. Therefore, when composite frame is designed, rational semi-rigid joints and shear connectors should be chosen. Through quantitative analysis, the optimum design is conducted in order to make full use of the advantages of materials and save cost.

On the basis of the moment, when the horizontal displacement peak value appears, the envelope diagrams of horizontal floor displacements are drawn and shown in Fig.8. The curves demonstrate that the difference between horizontal displacement peak values considering different factors becomes larger with the increase of floor. The horizontal displacement taking interface slip and semi-rigid joint into account grows fastest, and the horizontal displacement only considering interface slip grows more slowly. The one ignoring the effects of interface slip and semi-rigid joint is the most slowly growing curve. From the above, it becomes obvious that the effects of interface slip and semi-rigid joint on seismic response increase with the increase of floor, and the influence of semi-rigid joint is more remarkable.

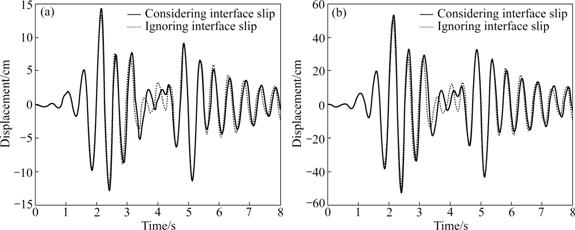
Fig.5 Influences of interface slip on elastic seismic response of composite frame: (a) The first floor; (d) The fourth floor

Fig.6 Influences of connection mode on elastic seismic response of composite frame: (a) The first floor; (d) The fourth floor

Fig.7 Horizontal displacement peak value of composite frame: (a) The first floor; (f) The sixth floor

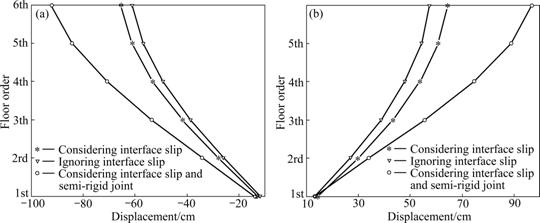
Fig.8 Horizontal displacement peak value envelop diagrams of composite frame floor under seismic loads: (a) The minimum value;    (b) The maximum value

5 Conclusions

(1) The analysis method for dynamic behavior and seismic response of composite frame considering the effects of interface slip and semi-rigid joint is presented. The method is convenient, effective and practical because of less nodal degrees of freedom.

(2) The interface slip of composite frame reduces its free vibration frequencies, especially to lower order frequencies.

(3) The joint stiffness has great effects on dynamic characteristic of composite frame. The free vibration frequencies of semi-rigid joint composite frame are obviously lower than that of rigid joint composite frame. When γ＜50, it is necessary to consider the effects of semi-rigid joint on dynamic characteristic of composite frame.

(4) The interface slip will increase the seismic response of composite frame, especially when α is relatively small, the seismic responses are more sensitive to interface slip.

(5) With the increase of joint rotational stiffness, the elastic seismic responses of composite frame do not decrease all the time. The trend is to increase firstly and then decrease. The influence of joint rotational stiffness on elastic seismic responses is more significant with the increase of floor and is related to the ratio of joint rotational stiffness to linear stiffness of composite frame.

References

[1] ELGHAZOULI A Y, CASTRO J M, IZZUDDIN B A. Seismic performance of composite moment-resisting frames [J]. Engineering Structure, 2008, 30: 1802-1819.

[2] LEON R T. Analysis and design problems for PR composite frames subjected to seismic loads [J]. Engineering Structure, 1998, 20: 364-371.

[3] PILUSO V, RIZZANO G, TOLONE I. Seismic reliability assessment of a two-story steel-concrete composite frame designed according to Eurocode 8 [J]. Structural Safety, 2009, 31(5): 383-395.

[4] JIANG Li-zhong, CAO Hua, YU Zhi-wu. Elastic-plastic earthquake response of steel-concrete composite frame structure [J]. Journal of Railway Science and Engineering, 2005, 2(3): 1-8. (in Chinese)

[5] JIANG Li-zhong, WANG Chen. Elastic-plastic earthquake response of steel-concrete composite frame structure [J]. Journal of Railway Science and Engineering, 2008, 5(2): 7-11. (in Chinese)

[6] ZONG Zhou-hong, LIN Dong-xin, FANG Zhen-zheng, QIU Fa-wei. Experimental research on seismic behavior of a two-story concrete filled steel tubular composite frame [J]. Journal of Building Structures, 2002, 23(2): 27-35. (in Chinese)

[7] SHI Qi-yin, ZHANG Ke-qiang, BAI Guo-liang. The experimental study of the behavior of the two-lay three-story composite frame composed of steel beams and steel concrete columns under cyclic-loading [J]. Journal of Shaanxi Institute of Technology, 1996, 12(3): 50-57. (in Chinese)

[8] LI T Q, MOORE D B, NETHERCOT D A, CHOO B S. The experimental behavior of a full-scale, semi-rigidly connected composite frame: overall considerations [J]. Journal of Constructional Steel Research, 1996, 39:167-191.

[9] WONG Y L, YU T, CHAN S L. A simplified analytical method for unbraced composite frames with semi-rigid connections [J]. Journal of Constructional Steel Research, 2007, 63: 961-969.

[10] WANG J F, LI G Q. A practical design method for semi-rigid composite frames under vertical loads [J]. Journal of Constructional Steel Research, 2008, 64: 176-189.

[11] WANG J F, LI G Q. Testing of semi-rigid steel-concrete composite frames subjected to vertical loads [J]. Engineering Structures, 2007, 29: 1903-1916.

[12] AYOUB A. A force-based model for composite steel-concrete beams with partial interaction [J]. Journal of Constructional Steel Research, 2005, 61: 387-414.

[13] RANZI G, ZONA A. A steel-concrete composite beam model with partial interaction including the shear deformability of the steel component [J]. Engineering Structures, 2007, 29: 3026-3041.

[14] NIE J G, CAI C S, M.ASCE P E. Steel-concrete composite beams considering shear slip effects [J]. Journal of Structural Engineering, 2003, 129(4): 495-506.

[15] LI Guo-qiang, ZHAO Xin. A finite element model of partial composite girders [J]. Chinese Quarterly of Mechanics, 2006, 27(3): 454-462. (in Chinese)

[16] LI Guo-qiang, SHEN Zu-yan. Elastic and elastic-plastic analysis and computation theory of steel frame system [M]. Shanghai: Shanghai Scientific and Technical Press, 2006: 7-201. (in Chinese)

[17] SHI Wen-long. Experimental and theoretical study on semi-rigid beam-to-column composite joints with flush end-plate connection [D]. Shanghai: Tongji University, 2006: 11-184. (in Chinese)

[18] HU Da-zhu, LI Guo-qiang, SUN Fei-fei. Practical analysis of natural periods for semi-rigidly connected multi-story composite frames [J]. World Earthquake Engineering, 2008, 24(2): 68-73. (in Chinese)

(Edited by CHEN Wei-ping)