
J. Cent. South Univ. (2019) 26: 3279-3294
DOI: https://doi.org/10.1007/s11771-019-4252-y

Role of matrix structure and flaw size distribution modification on deflection hardening behavior of polyvinyl alcohol fiber reinforced engineered cementitious composites (PVA-ECC)
Kamile TOSUN FELEKOGLU1, Eren GODEK2
1. Department of Civil Engineering, Dokuz Eylül University, Izmir 35390, Turkey;
2. Department of Construction Technology, Hitit University, Corum 19169, Turkey
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract:
The multiple cracking and deflection hardening performance of polyvinyl alcohol fiber reinforced engineered cementitious composites (PVA-ECC) under four-point flexural loading have been investigated. Matrices with different binder combinations and W/B ratios (from 0.44 to 0.78) providing satisfactory PVA fiber dispersion were specially designed. Effect of pre-existing flaw size distribution modification on deflection hardening behavior was comparatively studied by adding 3 mm diameter polyethylene beads into the mixtures (6% by total volume). Natural flaw size distributions of composites without beads were determined by cross sectional analysis. The crack number and crack width distributions of specimens after flexural loading were characterized and the possible causes of changes in multiple cracking and deflection hardening behavior by flaw size distribution modification were discussed. Promising results from the view point of deflection hardening behavior were obtained from metakaolin incorporated and flaw size distribution modified PVA-ECCs prepared with W/B=0.53. The dual roles of W/B ratio and superplasticizer content on flaw size distribution, cracking potential and fiber-matrix bond behavior were evaluated. Flaw size distribution modification is found beneficial in terms of ductility improvement at an optimized W/B ratio.
Key words:
Cite this article as:
Kamile TOSUN FELEKOGLU, Eren GODEK. Role of matrix structure and flaw size distribution modification on deflection hardening behavior of polyvinyl alcohol fiber reinforced engineered cementitious composites (PVA-ECC) [J]. Journal of Central South University, 2019, 26(12): 3279-3294.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-019-4252-y1 Introduction
Continuous reinforcing bars are placed at the appropriate locations of brittle concrete in order to withstand the imposed tensile and shear stresses. Fibers, on the other hand, are not efficient in withstanding the tensile stresses since they are discontinuous and randomly distributed throughout the cementitious matrix. Due to this reason, in most fiber reinforced cementitious composite (FRCC) applications, fibers are not used to improve the strength (either tensile or other) of cement based composites. Rather, the role of fibers is to control or limit the cracking of composite, and to alter the behavior of composite once the matrix has cracked. Presence of fibers in throughout the composite provides effective controlled local cracking if there are enough homogeneously distributed fibers in matrix. However, fibers may also improve the ductility of the material or more properly, its energy absorption capacity [1].
The advantages of fiber reinforcement listed in the previous paragraph is often limited due to the lack of proper fiber-matrix compatibility, and in most cases FRCC exhibits tensile softening and/or deflection softening behavior in tension and flexural loading, respectively. Failure of such ordinary FRCC is usually characterized by single crack opening and widening process. In this failure mode, the load-bearing ability drops gradually rather than catastrophically as the fracture propagates [2]. By focusing on the fiber-matrix and interface design parameters more systematically, high performance fiber reinforced cementitious composites (HPFRCCs) presenting strain hardening and multiple cracking behaviors in both tension and bending are successfully developed in the last two decades [3-6]. These short fiber (metallic and/or non-metallic) reinforced cement based composites usually contain less than 2%-3% fiber by volume, which satisfies the ease of processing [7]. A specially designed and optimized composite from the viewpoints of matrix packing density, fiber strength and interface bond properties is required for ultra-high performance version of HPFRCCs [8].
Over the past two decades, LI’s research group at the University of Michigan, USA has developed a highly ductile version of HPFRCC known as engineered cementitious composite (ECC), popularly known as “bendable concrete” [9, 10]. ECC exhibits remarkable tensile strain (3%-7%) and deflection capacity with a moderate volume fraction (equal to or less than 2%) of short polymeric fibers (usually PVA fibers) which are at least 100 times higher than a structural concrete. At the same time, compressive strength of ECC is similar to that of moderate and high strength concretes (40-70 MPa) [11]. When an ECC is loaded (flexure or shear) to beyond the elastic range, the inelastic deformation is associated by micro- cracking with continued load carrying capacity across these cracks. The crack width first increases, but reaches to a more or less steady state value beyond about 1% strain, the crack width stabilizes at a definite value (usually less than 100 μm) depending on matrix, fiber and interface properties of ECCs. Multiple cracking provides a means of energy dissipation at the material level and prevents localized fracture in the structure [12]. The ductility of ECC is the sum total of distributed deformation resulting from the micro-cracks. The tight crack width in ECC has advantageous implications on structural durability, and the minimization of repair needs subsequent to severe loading of ECC members [9].
2 Design and concept of tailoring matrix flaw size distribution of ECC
The theoretical framework of ECC design was first established in early 90’s and efforts to reach better models have continued since then [13]. According to micromechanics based design theory of ECC, two complimentary criteria have been proposed to attain a multiple micro-cracking response. These are the strength criterion and the energy criterion. Details of the micromechanical model and a brief summary of recent developments can be found in Refs. [14, 15], respectively.
In order to achieve energy criterion, fiber bridging strength (σo) should be increased by using a high fiber volume fraction, a strong fiber, a better fiber dispersion, and/or strong fiber/matrix bond. Due to cost restraints and poor workability related inhomogeneous fiber dispersion, a high fiber volume fraction (>2% by volume) is not applicable with conventional mixing and molding techniques. A strong fiber also incurs higher material cost. A strong fiber/matrix bond can be engineered; however, excessively high bond leads to fiber rupture that violates the energy criterion. Tuning the fiber’s mechanical and geometric properties and the fiber/matrix interface properties for a given matrix is a key element in ECC design [15].
On the other hand, the strength criterion states that the tensile stress to initiate a crack from a pre-existing flaw (σcr: cracking strength) must be below the bridging capacity of the fibers (σo) crossing that crack. For a brittle matrix composite such as HPFRCC, σcr is determined by the matrix fracture toughness (Km) and the largest crack-like flaw (c) in the section normal to the maximum principal stress. Low Km brings low σcr and leads to high strain and deflection capacity for ECC design at given fiber and interface properties [16].Recently, there are results implying that the flaw size is a key parameter that correlates well with matrix cracking strength which directly can be correlated with the matrix fracture toughness [17]. The size and spatial distributions of pre-existing flaws exist in cement based matrix (entrapped air voids, weak boundaries between phases, cracks induced by shrinkage), possess random nature and strongly depend on mixing, compacting and curing conditions. In practice it is difficult to quantitatively characterize the natural flaw system. Usually specimens sliced normal to longitudinal direction into sections using a diamond saw, and the cutting surface is observed under optical microscope to examine the large pore size distribution at this section [18, 19].
The role of flaw size and distribution on multiple cracking performances can be explained as follows: crack initiation starts at the largest and most favorably oriented flaw and progressively works its way to smaller and smaller flaws as the tensile load increases. On each crack plane, the load shed by the matrix is taken over by the bridging fibers. The load carried by the bridging fiber is a function of fiber bridging capacity (σo), varies from one crack plane to another due to the inevitable spatial non-uniformity in fiber dispersion. The micro-crack density typically increases with increasing tensile load. If actual tensile stress exceeds the fiber bridging capacity on any given crack plane, that crack localizes into a fracture that terminates the multiple cracking process. It should be noted that very small flaws with cracking strength higher than the lowest fiber bridging capacity of already existing cracked planes will never be activated. This leads to the inefficient use of composite multiple cracking potential. Therefore, to achieve saturated multiple cracking, sufficient number of large flaws must exist in the matrix. Only those flaws larger than critical flaw size (cmc) can be activated prior to reaching fiber bridging stress and contribute to multiple cracking [18].
The viability of achieving saturated multiple cracking in ECC though tailoring of pre-existing flaw size distribution in matrix under tensile loading is demonstrated [18]. Adding sufficient number of single size artificial flaws improved the multiple cracking behavior of composites. The concept of tailoring matrix flaw size distribution for saturated multiple cracking is schematically presented in Figure 1 [18]. The introduced artificial flaws should have sizes larger than the lower bound of critical flaw size (cmc). The introduced artificial flaws have sizes larger than cmc and will be superposed to natural flaw system. In practice the size of the particle used as artificial flaws can be selected as the size of the largest voids observed in the cracked sections. Since the σcr is bounded by steady state stress, larger flaws will not significantly influence or slightly reduce σcr.

Figure 1 Scheme of flaw size tailoring for ECC mix (adopted from Ref. [12]):
In this study, similar concept introduced by Ref. [18] which explained in previous paragraph is applied under flexural loading. The effect of polymeric bead addition (as artificial flaws) in four different PVA-ECCs prepared with varying W/B ratios and metakaolin content is investigated in terms of flexural deflection capacity and multiple cracking potential. For this purpose, load-mid-point deflection behavior of PVA-ECCs under four-point flexural loading is tested. Natural flaw size distribution throughout the composites in the absence of artificial flaws was determined via cross sectional analysis. The effects of flaw size distribution modification on first cracking strength, flexural strength, deflection capacity and relative toughness is discussed with respect to W/B ratio. Two different indices have been proposed based on toughness and deflection potential. The effectiveness of these indices in terms of reflecting deflection hardening potential is also compared with relative toughness values. Possible causes of improvements in crack density and equivalent total crack widths by the addition of polymeric beads are discussed with the aid of flaw size distribution and residual crack analyses.
3 Experimental program
3.1 Materials, mixing sequence and mix proportions
CEM I 42.5R type Portland cement and metakaolin supplied from Cimentas Cement Plant-Turkey and Powerpozz-USA are used as binder phases, respectively. The chemical, physical and mechanical properties of Portland cement procured from supplier are presented in Tables 1 and 2, respectively.
Table 1 Chemical composition of Portland cement (mass fraction, %)

Table 2 Physical and mechanical properties of portland cement
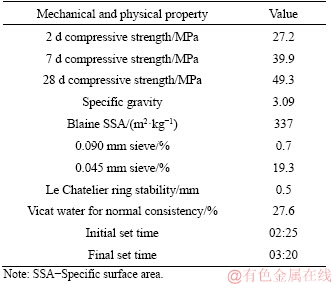
The chemical composition of metakaolin consists of 52%-54% SiO2 and 42%-44% Al2O3 and some impurities (Fe2O3, CaO, MgO, Na2O, K2O, TiO2 and SO3) less than 3%. Limestone powder with high CaCO3 purity (99%) is used as inert aggregate phase. The specific gravity and Blaine fineness values of limestone powder are 2.65 and 538 m2/kg, respectively. In order to maintain appropriate workability, a polycarboxylate-based superplasticizer is also employed in matrix compositions. The pH, specific gravity and solid content values of this admixture are 6.5%, 1.18%-1.20% and 35.7%, respectively. PVA fiber with 39 μm diameter and 12 mm length from Kuraray (Japan) is used for the purpose of providing deflection hardening behavior. The specific gravity, tensile strength, elastic modulus and elongation capacity of PVA fibers are 1.3,1620 MPa, 42.8 GPa and 6%, respectively. Single size polyethylene (PE) beads with a diameter of 3 mm are used as artificial flaws for the purpose of matrix flaw size distribution modification. PE beads are supplied by PETKIM-Turkey (YYPE I668). Due to the highly hydrophobic and smooth surface structure of PE beads, no bonding is expected between cement matrix and bead surface. Bead-matrix interface will behave like an embedded crack and act as single size artificial flaw in composites [18]. Since the maximum flaw size observed at the cracked sections of specimens with natural flaws was usually 3-8 mm, bead size was selected as 3 mm which is assumed to be greater than critical flaw size (cmc) (Figure 1(b)).
Hobart mixer is used for mixing approximately 1.5 dm3 fresh mortar for each set of three composites. First, cement, limestone powder and metakaolin (if exist in the mix) are dry mixed for 30 s at low speed ((62±5) r/min) and then water + superplasticizer is added into the mix and continued to mix at high speed ((125±10) r/min) for 3 min until a homogeneous slurry is obtained. The fibers are then slowly added to the wet mix and high speed mixing is prolonged until the fibers will disperse in the mix. In the case of flaw size distribution modified specimen preparation, 1 min of additional high speed mixing is performed after bead addition. The workability of fiber reinforced mixtures has been measured by using a flow-table conforming the ASTM C1437 [20] standard requirements. Flow diameters of fiber reinforced fresh mixtures are maintained 130-150 mm by adjusting the amount of polycarboxylate-based superplasticizers. For each mix, three prismatic specimens of 25 mm×60 mm×285 mm are cast with slight vibration. Another set of 1.5 dm3 of mixing is performed with the same mixture proportion and three prismatic specimens of 40 mm×40 mm×160 mm are cast for compressive strength tests confirming to ASTM C349 [21]. Specimens are demolded for 1 d after casting and subjected to lime saturated water curing at (20±1) °C for 28 d.
The mixture proportions and required superplasticizer dosages of four mixtures prepared with different W/B ratios are presented in Table 3. Matrices with various W/B ratios are selected for the purpose of investigating the influence matrix fracture toughness on the flexural cracking behavior. In normal ECC mix without explicit control of flaw size distribution, low matrix toughness is often used [22]. Higher W/B ratios providing relatively lower matrix toughness are more suitable for ECC design, provided that enough bond still present between fiber and matrix [18]. Fiber dosage is kept constant for all mixtures (2% by total volume).
Binder phase of the first mix is only cement (845 kg/m3) and W/B ratio is 0.44. This set is labeled as 0.44C. This mixture is designed as the strongest one in terms of strength. Binder phase of the second mix is equally cement and metakaolin (372 kg/m3 for each). Metakaolin is used as a viscosity enhancer for the purpose of improving the fiber dispersion homogeneity. However, high mixing water demand of metakaolin increased the required W/B ratio to 0.53 and superplasticizer demand also increased for a constant workability (to achieve similar to that of 0.44C). This mixture is labeled as 0.53M. Increase in the W/B ratio decreased the superplasticizer demand of third and fourth mixtures (labeled as 0.63M and 0.78M). Another set of all mixtures was prepared with 6% bead addition by total volume and labeled with additional capital “B”. The fresh rheology of ECC matrix directly governs the fiber dispersion, which also influences both the feasibility and density of multiple cracking. Poor fiber distribution will lead to a reduced effective fiber dosage at the weakest cross section within the specimen [22]. Due to this reason, fiber homogeneity is ensured for all mixtures by checking the presence of any fiber coagulation or balling in fresh mixes.
3.2 Mechanical experiments
3.2.1 Flexural test methodology
Four-point flexural loading tests are performed by using a deformation controlled testing machine (Figure 2). The mid-span length of 86.7 mm is one-third of the simply supported clear span length of 260 mm. Mid-span deflection is measured with an LVDT and deflection rate is kept constant throughout the testing interval (1 mm/min). The resulting load vs mid-span deflection curves and the area shed by three individual specimens are plotted up to 18 mm mid-point deflection value (Figure 3).
The behaviors of deflection hardening composites under flexural loading are different from ordinary fiber reinforced concrete. Due to this reason, parameters describing their flexural performance derived from load-deflection curve are schematically presented in Figure 4.
Table 3 Matrix mix proportions


Figure 2 Schematically presentation of three-point flexural test setup (a), three-point flexural test setup (b), and presentation of deflection and multiple-cracking (c)

Figure 3 Resulting load vs mid-point deflection curves and area shed by three individual specimens:

Figure 4 Parameters of deflection hardening composites derived from load-deflection curves
The first sudden drop at load carrying capacity is accepted as the first cracking point which is assumed to be close to the limit of proportionality (LOP). However, the determination of first cracking point or LOP is complicated for some samples when there is a continuous slope change at the initial linear portion of load displacement curves [23]. In this case, two tangents were prolonged from the linear portions of curves and the vertical intersection point with the curve was accepted as the first cracking point. Similar methodology was previously applied by KIM et al [5] and SHAIKH [7] for the determination of LOP point. The first cracking strength and deflection at first cracking (δLOP) of composites are determined using the first cracking load data (PLOP) and corresponding deflection value.
The ultimate flexural strengths of composites are determined using the point where softening starts in the load-deflection curve. Peak load (Ppeak) is the y-axis value and corresponding x-axis value is the deflection capacity (δpeak) of this point.
The maximum load is usually higher than the first cracking load due to multiple cracking and deflection hardening behavior of ECC. Deflection hardening PVA-ECC exhibits much higher energy absorption capacity compared to deflection softening composites. The energy absorption of fiber composites is also termed as toughness which is defined as the area under the load-deflection curve up to a given deflection. The current ASTM C 1609 [24] specifies the deflection limit up to 1/150th of the span. However, depending upon the composite’s ductility, this limit needs to be adjusted and for deflection hardening fiber composites [5, 7]. For this reason, calculation of toughness parameters at a definite deflection ratio is not capable of reflecting the exact toughness capacity of deflection hardening composites [7]. Various attempts for calculating the toughness values can be found in Refs. [25, 26]. As an alternative methodology, relative toughness (Tpeak) value of each composite has been determined by integrating the area under the load-deflection curve until the deflection capacity is consumed which corresponds to peak load point [7]. Furthermore, a toughness index proposed by SHAIKH [7] is calculated as Ipeak. Ipeak is the ratio of Tpeak to the area of the load–deflection curve up to limit of proportionality (TLOP). According to Refs. [5, 7], the numerator of the index is considered the energy up to deflection corresponding to peak load and the denominator is considered the elastic energy. Higher Ipeak values indicate more ductile composites exhibiting deflection hardening behavior.
3.2.2 Compression test methodology
Compressive strength tests were also performed for the purpose of controlling the structural strength grade of ECCs. ASTM C349 [21] standard was used. Specimens with 40 mm×40 mm×160 mm size were prepared with the same mixing, molding and curing conditions with the flexural test specimens. Specimens were broken into two parts under third point flexural tests at 28th day. Compression tests were performed to the broken portions of three 40 mm×40 mm×160 mm prismatic samples for each series. The compressive strengths were calculated and their averages were considered as the compressive strength for the corresponding series.
3.3 Residual crack analysis
The residual crack widths and crack counts of all specimens after loading are determined by linear line intersection point counting method. Two lines are drawn to the cracked surface of unloaded specimen. The width of each crack intersecting this line is captured with a portable optical microscope (Dino-lite pro up to 500× magnification). Crack widths are measured from 5 megapixel resolution images by Dinocapture software. Scale calibration was performed for each corresponding magnification. Residual cracks with largest width are assumed as major crack based on observations on cracked specimens. The fiber bridging capacity was exhausted at these major crack sections and the number of these major cracks was usually less than three and in most cases only a single crack was enlarged while others was closing.
The minor cracks exhibit elastic recovery after unloading the specimens owing to their steady state conditions. However, major cracks have no or negligible elastic recovery after unloading the specimens since these cracks are significantly widened after peak load (Griffith type crack). Therefore, these major crack or cracks are excluded from the crack number and width analysis in order to calculate relatively high accurate crack widths.
3.4 Natural flaw size distribution analysis
After the completion of crack analysis, each prismatic composite was sliced down to the longitudinal direction as shown in Figure 5 by using a ceramic saw. The cutting surface of each piece was observed under optical microscope to examine the large pore (flaw) size (>1 mm) distribution at individual section. Totally 8 pieces with approximate thickness of 10-15 mm are scanned from each specimen.
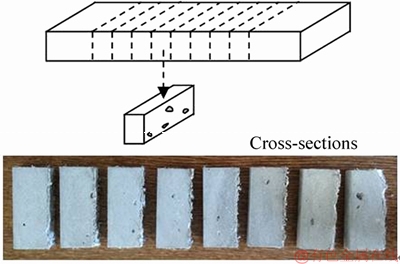
Figure 5 Prismatic composite (25 mm×60 mm×285 mm) slices and cross-sections of a specimen used in macro flaw size distribution analysis
4 Results and discussion
4.1 First cracking and flexural strength
The calculated average first cracking (σLOP) and flexural stress (σpeak) values of specimens with natural flaw size distribution and with bead modification according to the method described in Section 3.2 are presented in Figures 6(a) and (b), respectively. Standard deviations of three specimens are also marked with lines. In general, both stress values were decreased by increasing the W/B ratio. The highest flexural strength values were derived from 0.44C mix (highest cement content and lowest W/B ratio). This is expectable since hydration reactions in the presence of high mixing water contents produces more capillary porosity which decreases ultimate strengths. Addition of PE beads also slightly decreased the first cracking and flexural strength values with a few exceptions.
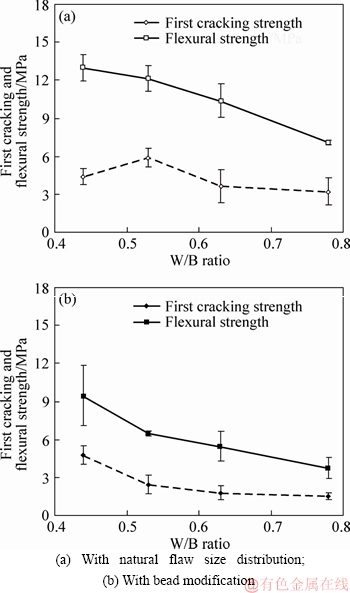
Figure 6 First cracking and flexural strength values of specimens:
4.2 Deflection at first cracking and peak load deflection capacity
Deflection values at first cracking (δLOP) and deflection capacities (δpeak) obtained from load vs mid-span deflection curves are plotted in Figure 7. Standard deviations of three specimens are also marked with lines. δLOP values are in the range of 0.1-0.3 mm for both unmodified and bead modified specimens and no relationship was found between δLOP and W/B ratio.
Deflection capacity (δpeak) of specimens increased with increasing W/B ratio up to a limit, and then decreased in the case of unmodified composites (Figure 7). Lower matrix fracture toughness due to increasing W/B ratio decreases the matrix cracking strength and as a result deflection capacity can be improved. Increasing W/B ratio also affects the transition zone between fiber and matrix and interface bond decreases at higher W/B ratios. In particular, high affinity of PVA fibers with cementitious matrix may result in fiber rupture due to excessive bond. A tolerable reduction in the fiber-matrix bond is beneficial for the improvement of deflection capacity of PVA fibers. If fiber debonding rather than rupture is observed, PVA fiber provides slip hardening phenomena after debonding and additional slippage at increasing stress contributes to deflection capacity of composite [27, 28]. However, excessive reduction in fiber-matrix bond may cause premature fiber slipping without any slip hardening process. Due to the dual role of fracture toughness and fiber matrix bond, there is an optimum W/B ratio for achieving the highest deflection capacity. In this study, the optimum W/B value is 0.63 for unmodified specimens.
Similar trend is observed in the case of bead modified specimens. Comparatively much higher deflection capacities were reached at the same W/B ratio (Figure 7). Highest deflection capacity is derived from composites with W/B=0.53 (8.71 mm). Furthermore, standard deviation of three specimens of this composite is comparatively low which indicates the consistent and robust deflection hardening behavior for these composites. However, the performance of composites at higher W/B ratio is more fluctuating and exhibits higher standard deviations.
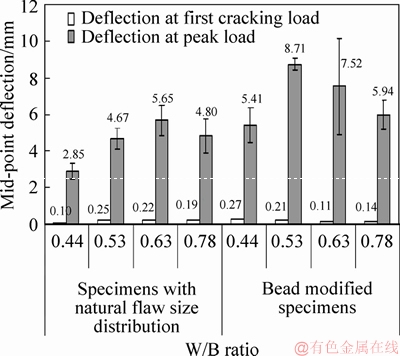
Figure 7 Deflection values at first cracking (dLOP) and deflection capacities (dpeak) obtained from load vs mid-span deflection curves
4.3 Effective flexural toughness, toughness and deflection hardening indices
Relative flexural toughness (Tpeak) values of each composite determined according to the method described in Section 3.2 are presented in Figure 8. Highest Tpeak values are derived from the mix with W/B=0.53 in both unmodified and modified specimens (above 6 kN·mm). Higher or lower W/B ratios cause decrease and/or significant fluctuations in Tpeak values. Addition of artificial flaws improves the Tpeak values up to W/B=0.53. However, toughness decrease is observed when artificial flaws are added to the mixtures at W/B ratios higher than 0.53.
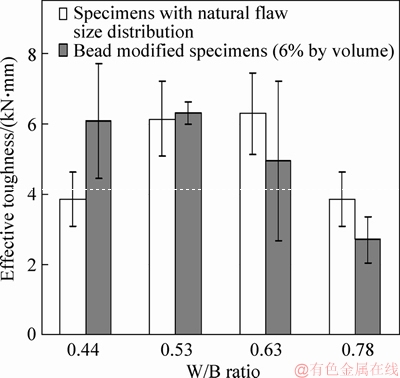
Figure 8 Relative flexural toughness (Tpeak) values of composites
In some cases, Tpeak values are unable to reflect the deflection capacity of composites. While the deflection capacity of 0.53M specimens with natural flaw size distribution (4.67 mm) is nearly the half of bead modified 0.53MB specimens (8.71 mm), the toughness values of both specimens are nearly the same. Due to this reason, effective toughness (Ipeak) and deflection hardening indices (IDH=δpeak/δLOP) are also calculated and presented in Figures 9(a) and (b), respectively. Similar trend is observed by increasing W/B ratio in both unmodified and modified cases. Bead modification improved the Ipeak and deflection hardening index (IDH) for specimens with W/B ratios higher than 0.53. On the other hand, due to the variability of load-deflection curves of bead modified 0.44CB specimens, Ipeak and IDH are lower than that of unmodified composites (0.44C). 0.53MB and 0.63MB are the best composites in terms of toughness and deflection hardening indices. However, 0.53MB can be selected due to the lower variation in indices values.

Figure 9 Effective toughness (a) and deflection hardening (b) indices of specimens
4.4 Crack density, average residual crack width and crack width distribution
Average number of cracks and residual crack widths formed after flexural loading are listed in Table 4. Bead addition significantly increases the number of cracks of specimens by two to three folds depending on W/B ratio. At the same time, bead modification decreases the residual crack widths (nearly half of unmodified) at all W/B ratios. There is no significant trend in terms of crack number or width as the function of W/B ratio for unmodified specimens. However, crack number decreases and simultaneously crack width increases with increasing W/B ratio for bead modified specimens. Crack number or average crack widths are not solely able to indicate the effective deflection hardening potential of composites since they are changing at the same time. Due to this reason, the parameter of equivalent total length of residual crack width is also calculated by multiplying the number of cracks with residual crack width of each individual specimen. Equivalent total length of residual crack width values against net deflection values at the stage of hardening (δpeak-δLOP) are plotted in Figure 10. According to this plot, there is a strong positive correlation between this value and net deflection values at the stage of hardening in both cases. The best performance in terms of saturated multiple cracking potential is derived from 0.53MB where standard deviation related error bars are also minimized. Equivalent total length of residual crack width is found to be a good indicator of effective deflection hardening potential and better reflects the variability of composites compared to toughness value and deflection hardening indices.
Residual crack width distributions of composites up to 300 μm with 20 μm intervals are plotted in Figure 11. Comparative crack width distributions of 0.44C and 0.44CB specimens are plotted in Figure 11(a). Most of the crack widths are lower than 120 μm when a high strength matrix is employed (W/B=0.44). The crack widths significantly shifted to lower values with the addition of PE beads. Researchers should note that a narrow crack width distribution is identical for ECC composites to ensure desired durability properties which is not examined in the concept of this study [9]. Replacement of half of cement with metakaolin and increase in W/B ratio caused a more dispersed crack width distribution (Figure 11(b), W/B=0.53). If 0.53M and 0.53MB curves are compared, it is valid that the presence of larger crack widths significantly reduces by PE bead modification. A major portion of residual crack widths are less than 140 μm for 0.53MB. Note that number of cracks are 26±3 and the average crack width is 69 μm for this set. Further increase in W/B ratio increased the scatter of crack width distribution as seen in the case of 0.63M (Figure 11(c)). Bead addition at this W/B ratio decreases the number of wider cracks (>120 μm) and increased the number of narrow cracks (<120 μm). However, there is still significant amount of wider cracks after bead modification. Presence of both narrow and wider cracks at 0.63MB specimens may be the source of high variation in crack number (20±13). At the highest W/B ratio, the role of bead modification on crack width distribution is not very significant (Figure 11(d)).
Table 4 Residual crack characteristics of PVA-ECCs


Figure 10 Positive correlation between equivalent total length of residual crack width and net deflection (Error bars indicate ±standard deviation)

Figure 11 Residual crack width distributions up to 300 mm with 20 mm intervals
Cumulative percentages of residual crack width distribution curves are plotted for the purpose of distinguishing the effects of different matrix structures (Figure 12). Nearly 93% of residual crack width is less than 100 μm for 0.44C composites. The ratio of narrow cracks less than 100 μm to total crack number decreases for composites prepared with higher W/B ratios with an exception at the highest W/B ratio (0.78M: 79%) (Figure 12(a)). Since the number of cracks counted at this composite is very low, narrow residual cracks widths are useless in terms of improved ductility. Due to the insufficient fiber bridging potential as a consequence of premature bond strength (extremely high W/B ratio significantly decreases the fiber-matrix bond), these composites fail to provide enough fiber bridging strength to satisfy the energy criteria requirements of ECC micromechanical theory. On the other hand, W/B=0.53 and W/B=0.63 seem to be more appropriate for the purpose of ductility improvement with a potentially higher fiber bridging strength. However, their narrow crack widths less than 100 μm are nearly half of the total crack count, which should be shifted to higher values. PE bead addition increases this ratio up to 80% which brings ductility improvement for both 0.53M and 0.63M composites (Figure 12(b)).

Figure 12 Cumulative crack width distributions:
Lowering the matrix fracture toughness by increasing W/B ratio positively influences the cracking potential of composites. At the same time, increasing the W/B ratio could decrease the fiber-matrix bond strength and fiber bridging strength simultaneously. Since PVA fibers possess high chemical affinity with cement matrix, extremely high bond strength may cause fiber rupture. Due to this reason, moderate bond strength is more appropriate for PVA-ECC composites for the purpose of presenting initial debonding and then slip with hardening (i.e. W/B=0.53-0.63). From this point of view, an optimum W/B ratio may be suggested as 0.53 in the presence of PE beads. If fiber-matrix bond is extremely reduced by matrix modification, average crack widths will enlarge and fibers at that opening cannot transfer the stress to the sides of crack opening. In most cases, a residual crack width below 100 μm is suitable to maintain the fiber bridging stress [14]. Based on the results presented in Figure 12(a), it can be concluded that multiple cracking and deflection hardening potential of 0.53M and 0.63M composites are not effectively utilized since nearly half of the crack widths are larger than 100 μm. As seen in Figure 12(b), modification of flaw size distribution by bead addition significantly increases the narrow crack width (less than 100 μm) of both 0.53MB and 0.63MB composites (above 80%).
Together considering the effective toughness, deflection capacity and crack width distribution results, 0.53MB composite seems to be the best alternative as a PVA-ECC exhibiting saturated deflection hardening behavior. Lower fiber-matrix bond strength of 0.63MB composite compared 0.53MB might be responsible for the variations in effective toughness and ductility values.
4.5 Cross-sectional flaw size distribution analysis
The measured flaw size distribution with 1 mm intervals up to 8 mm is plotted in Figure 13. Note that pores smaller than 1 mm equivalent diameter are not included to the flaw size distribution graphs. Large flaws are usually entrapped air voids. Size range of maximum flaws is increased from 4-5 mm up to 7-8 mm by increasing W/B ratio and by reducing superplasticizer dosage simultaneously. Since superplasticizers are employed to improve the compactability of mixtures, this kind of macro-pore structure modification can be expected despite the presence of higher amounts of water in mixtures. Numbers of flaws larger than 3 mm counted from cross-sections of three specimens of 0.44C, 0.53M, 0.63M and 0.78M are 9, 10, 35 and 28, respectively. Increase in maximum flaw size decreases the flexural strength and first cracking strength of composites. Since the presence of larger voids play a significant role in cracking initiation, the deflection capacity of composites is improved except 0.78M composites. There seems an optimum maximum flaw size for the highest deflection capacity. From the view point of matrix fracture energy, a lower cracking strength by employing a high W/B ratio is beneficial for crack initiation. However, excessively increasing the W/B ratio may negatively affect the fiber-matrix interface behavior as observed in 0.78M composites.

Figure 13 Natural flaw size distribution of 0.44C, 0.53M, 0.63M and 0.78M composites
The first cracking and flexural strengths of composites slightly decrease with the addition of artificial flaws (6% beads) (Figure 6). In steady state cracking, the matrix cracking strength is lower bounded by the steady state stress [12]. Since the size of the introduced artificial flaws is slightly less than the critical voids in matrix, presence of additional flaws has little adverse effect on matrix cracking strength.
The results show that through tailoring of pre-existing flaws (addition of 6% by volume of PE beads), deflection capacity and multiple cracking performances of composites can be improved (Figure 7, Table 4). A matrix design providing the targeted fiber-matrix interaction is the pre-condition of this improvement. Furthermore, a more robust multiple cracking performances with less variation in crack widths can be obtained. In mixes without explicit control of pre-existing flaws, large variation in tensile behavior may occur due to the flaw size sensitivity to processing. From this point, fiber- matrix bond behavior of 0.78M mixture is not suitable for consistent and robust multiple cracking (Table 4).
It should be noted that flaw size tailoring is only effective when the cracking strength at smaller flaws is higher than the fiber bridging capacity. Nevertheless, high cracking strength is typically the case in most HPFRCCs. On the other hand, the micro-pore structure of matrix (<1 mm) may also affect the matrix flexural strength and fracture energy [12]. Further study is needed to take the effect of composite micro-pore structure on multiple cracking potential into account.
4.6 Compressive strength
Compression test results are presented in Figure 14. Compressive strength values of ECCs are in the range of 30-70 MPa. Increase in W/B ratio decreases the compressive strength values which are in conformity with Abrams rule. It seems that 28 d is not enough to obtain the pozzolanic effect of metakaolin on compressive strength values. Higher W/B ratios are also responsible for the lower compressive strength of metakaolin incorporated specimens.
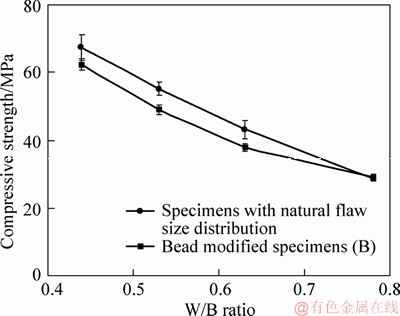
Figure 14 Compressive strength of ECCs with increasing W/B ratio (error bars indicate ±1 standard deviation)
A slight decrease in compressive strength is observed at all W/B ratios with the addition of 6% polymeric beads (maximum compression strength loss is less than 10%) (Figure 14). As reported in Section 4.1, this reduction is not as significant as in the case of flexural strength values. Such amounts of compressive strength loss is reasonable since pre-existing cracks or flaws usually close and stabilize under compression while acting as crack propagators under tension.
5 Conclusions
1) Optimum W/B ratio for achieving highest deflection capacity (5.63 mm at 260 mm span) is 0.63M for PVA-ECCs with natural flaw size distribution. Addition of PE beads improves the deflection capacity of all investigated PVA-ECCs and highest deflection capacity is obtained from 0.53MB mix (8.71 mm at 260 mm span).
2) Despite the improvements in deflection capacity, addition of PE beads slightly decreases the first cracking, flexural and compressive strength values with a few exceptions. However, strength values still can be accepted as similar to that of structural concrete values.
3) Flaw size distribution modification with bead addition significantly increases the number of cracks of specimens by two to three folds depending on W/B ratio. At the same time, bead modification decreases the residual crack widths (nearly half of unmodified) at all W/B ratios.
4) Relative flexural toughness (Tpeak) values may be unable to reflect the deflection capacity of composites exhibiting deflection hardening behavior such as ECC examined in this study. Due to this reason, effective toughness (Ipeak) and deflection hardening indices (IDH) are also calculated and found more effective to indicate the deflection capacity of composites.
5) Bead modification improves the Ipeak and IDH for specimens with W/B ratios higher than 0.53, 0.53MB and 0.63MB are the best composites in terms of toughness and deflection hardening indices. However, 0.53MB is preferable due to the lower variation in indices values.
6) Residual crack number or average crack widths are not solely able to indicate the effective deflection hardening potential of composites. The parameter of equivalent total length of residual crack width is proposed and a strong positive correlation is available between this value and net deflection values at the stage of deflection hardening in both cases.
7) The best performance in terms of saturated multiple cracking potential is derived from 0.53MB where standard deviation related error bars are also minimized. The number of cracks, average crack width and equivalent total length of residual crack width values of this composite are 26±3,(69±13) μm and 1.8 mm, respectively.
8) Natural flaw size distributions of PVA-ECCs are affected by W/B ratio and superplasticizer dosage. Size range of maximum flaws is increased from 4-5 mm up to 7-8 mm by increasing W/B ratio and by reducing superplasticizer dosage simultaneously. Increase in maximum flaw size decreases the flexural strength and first cracking strength of composites. Since the presence of larger voids plays a significant role in cracking initiation, deflection capacities of composites are improved except 0.78M composites. There seems an optimum maximum flaw size for the highest deflection capacity.
Acknowledgments
The authors would like to gratefully acknowledge the cooperation of Civil Engineers; Emin Demirkaya, Gülizar Sonmez, Selim Aykal AkIl and Sabri Kokmen for specimen preparation and testing are greatly appreciated. The authors are also thankful to Cimentas Group (Cementir Holding), Powerpozz-USA and Kuraray Co. Ltd. for supplying the materials used in this research.
References
[1] BENTUR A, MINDESS S. Fibre reinforced cementitious composites [M]. London: CRC Press, Technology & Engineering, 1990.
[2] LI J, ZHANG Y X. Evaluation of constitutive models of hybrid-fibre engineered cementitious composites under dynamic loadings [J]. Construction and Building Materials, 2012, 30: 149-160. DOI: 10.1016/j.conbuildmat.2011. 11.031.
[3] NAAMAN A E, REINHARDT H W. Proposed classification of HPFRC composites based on their tensile response [J]. Materials and Structures, 2006, 39(5): 547-555. DOI: 10.1617/ s11527-006-9103-2.
[4] LI V C, WU H C. Conditions for pseudo strain-hardening in fiber reinforced brittle matrix composites [J]. Journal of Applied Mechanics Review, 1992, 45(8): 390-398. DOI: 10.1115/1.3119767.
[5] KIM J D, NAAMAN A E, EL-TAWIL S. Comparative flexural behavior of four fiber reinforced cementitious composites [J]. Cement and Concrete Composites, 2008, 30(10): 917-928. DOI: 10.1016/j.cemconcomp.2008.08.002.
[6] KESKINATES M, FELEKOGLU B. The influence of mineral additive type and water/binder ratio on matrix phase rheology and multiple cracking potential of HTPP-ECC [J]. Construction and Building Materials, 2018, 173: 508-519. DOI: 10.1016/j.conbuildmat.2018. 04.038.
[7] SHAIKH F U A. Deflection hardening behavior of short fibre reinforced fly ash based geo-polymer composites [J]. Materials and Design, 2013, 50: 674-682. DOI: 10.1016/ j.matdes.2013.03.063.
[8] WILLE K, EL-TAWIL S, NAAMAN A E. Properties of strain hardening ultra-high performance fiber reinforced concrete (UHP-FRC) under direct tensile loading [J]. Cement and Concrete Composites, 2014, 48: 53-66. DOI: 10.1016/ j.cemconcomp.2013.12.015.
[9] LI V C. On engineered cementitious composites (ECC)—A review of the material and its applications [J]. Journal of Advanced Concrete Technology, 2003, 1(3): 215-230. DOI: 10.3151/jact.1.215.
[10] LI V C. Can concrete be bendable? [J]. American Scientist, 2012, 100(6): 484-493. https://www.researchgate.net/profile/ Victor_Li23/publication/275701732_Can_Concrete_Be_Bendable/links/5a53953d0f7e9bbc1056fbb0/Can-Concrete-Be-Bendable.pdf.
[11] RANADE R, ZHANG J, LYNCH J P, LI V C. Influence of micro-cracking on the composite resistivity of engineered cementitious composites [J]. Cement and Concrete Research, 2014, 58: 1-12. DOI: 10.1016/j.cemconres. 2014.01.002.
[12] WANG S. Micromechanics based matrix design for engineered cementitious composites [D]. USA: The University of Michigan, 2005. https://deepblue.lib.umich. edu/handle/2027.42/125251.
[13] KANDA T, LI V C. Effect of fiber strength and fiber-matrix interface on crack bridging in cement composites [J]. Journal of Engineering Mechanics, 1999, 125(3): 290-299. DOI: 10.1061/(ASCE)0733-9399(1999)125:3(290).
[14] LI V C, WANG S, WU C. Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite (PVA-ECC) [J]. ACI Materials Journal, 2001, 98(6): 483-492. https://www.researchgate.net/profile/Victor_Li23/ publication/279888212_Tensile_strain-hardening_behavior_or_polyvinyl_alcohol_engineered_cementitious_composite_PVA-ECC/links/58c6f96a4585150ab420dd1d/Tensile-strain-hardening-behavior-or-polyvinyl-alcohol-engineered-cementitious-composite-PVA-ECC.pdf.
[15] LI V C. Tailoring ECC for special attributes: A review [J]. International Journal of Concrete Structures and Materials, 2012b, 6(3): 135-144. DOI: 10.1007/s40069-012- 0018-8.
[16] LI V C, MISHRA D K, WU H C. Matrix design for pseudo- strain-hardening fibre reinforced cementitious composites [J]. Materials and Structures, 1995, 28(10): 586-595. DOI: 10.1007/BF02473191.
[17] LU C, LI V C, LEUNG C K. Flaw characterization and correlation with cracking strength in engineered cementitious composites (ECC) [J]. Cement and Concrete Research, 2018, 107: 64-74. DOI: 10.1016/j.cemconres.2018.02.024.
[18] WANG S, LI V C. Tailoring of pre-existing flaws in ECC matrix for saturated strain hardening [C]// Proceedings of FRAMCOS-5. Vail, Colorado, 2004: 1005-1012. https:// deepblue.lib.umich.edu/bitstream/handle/2027.42/84774/WangFramcos5.pdf?sequence=1&isAllowed=y.
[19] LI V C, WANG S. Microstructure variability and macroscopic composite properties of high performance fiber reinforced cementitious composites [J]. Probabilistic Engineering Mechanics, 2006, 21(3): 201-206. DOI: 10.1016/j.probengmech.2005.10.008.
[20] ASTM C1437. Standard test method for flow of hydraulic cement mortar [S]. ASTM International.
[21] ASTM C349. Standard test method for compressive strength of hydraulic-cement mortars (Using portions of prisms broken in flexure) [S]. ASTM International. DOI: 10.1520/ C0349-18.
[22] LI M, LI V C. Rheology, fiber dispersion, and robust properties of engineered cementitious composites [J]. Materials and Structures, 2013, 46(3): 405-420. DOI: 10.1617/s11527-012-9909-z.
[23] KANDA T, LI V C. Practical design criteria for saturated pseudo strain hardening behavior in ECC [J]. Journal of Advanced Concrete Technology, 2006, 4(1): 59-72. DOI: 10.3151/jact.4.59.
[24] ASTM C1609/C1609M. Standard test method for flexural performance of fiber-reinforced concrete (Using beam with third-point loading) [S]. ASTM International. DOI: 10.1520/ C1609_C1609M-12.
[25] TONOLI G H D, RODRIGUES FILHO U P, SAVASTANO H Jr, BRAS J, BELGACEM M N, LAHR F R. Cellulose modified fibres in cement based composites [J]. Composites Part A: Applied Science and Manufacturing, 2009, 40(12): 2046-2053. DOI: 10.1016/j.compositesa.2009.09.016.
[26] ZHOU J, PAN J, LEUNG C. Mechanical behavior of fiber-reinforced engineered cementitious composites in uniaxial compression [J]. Journal of Materials in Civil Engineering, 2015, 27(1): 04014111. DOI: 10.1061/ (ASCE)MT.1943-5533.0001034.
[27] KANDA T, LI V C. Interface property and apparent strength of high-strength hydrophilic fiber in cement matrix [J]. Journal of Materials in Civil Engineering, 1998, 10(1): 5-13. DOI: 10.1061/(ASCE)0899-1561(1998)10:1(5).
[28] LI V C, WU C, WANG S, OGAWA A, SAITO T. Interface tailoring for strain-hardening polyvinyl alcohol-engineered cementitious composite (PVA-ECC) [J]. Materials Journal, 2002, 99(5): 463-472. https://www.researchgate.net/profile/ Victor_Li23/publication/280224066_Interface_Tailoring_for_Strain-hardening_PVA-ECC/links/58c6f9afa6fdccde55e4134d/Interface-Tailoring-for-Strain-hardening-PVA-ECC.pdf.
(Edited by FANG Jing-hua)
中文导读
基体结构和缺陷尺寸分布改性对聚乙烯醇纤维增强工程水泥基复合材料(PVA-ECC)挠度硬化行为的影响
摘要:研究了聚乙烯醇纤维增强工程水泥基复合材料(PVA-ECC)在四点弯曲载荷作用下的多重开裂和挠度硬化性能, 设计了不同粘结剂组合和水胶比(W/B)(0.44~0.78)的矩阵,使PVA纤维得到了较好的分散。通过在混合物中加入直径为3 mm的聚乙烯微球(总体积为6%),比较研究了预先存在的缺陷尺寸分布修正对挠度硬化行为的影响。通过横断面分析,确定了无珠复合材料的自然缺陷尺寸分布。对弯曲加载后试件的裂纹数和裂纹宽度分布进行了表征,并讨论了缺陷尺寸分布改性引起多次裂纹和挠度硬化行为变化的可能原因。在W/B=0.53的条件下制备了含偏高岭土和缺陷尺寸分布改性的PVA-ECC, 得到了较好的挠度硬化行为。分析了W/B比和超增塑剂含量对缺陷尺寸分布、潜在开裂、和纤维-基体粘结行为的双重作用。在优化的W/B比下,发现了有利于改善延展性的尺寸分布修正。
关键词:纤维增强胶凝复合材料;偏高岭土;挠度硬化;多重开裂;缺陷尺寸分布
Foundation item: Project(114M246) supported by the Scientific and Technological Research Council of Turkey
Received date: 2018-10-15; Accepted date: 2019-02-26
Corresponding author: Eren GODEK, PhD Candidate, Lecturer; Tel: +90-364-2230800; E-mail: erengodek@hitit.edu.tr; ORCID: 0000-0002-3427-2317
Abstract: The multiple cracking and deflection hardening performance of polyvinyl alcohol fiber reinforced engineered cementitious composites (PVA-ECC) under four-point flexural loading have been investigated. Matrices with different binder combinations and W/B ratios (from 0.44 to 0.78) providing satisfactory PVA fiber dispersion were specially designed. Effect of pre-existing flaw size distribution modification on deflection hardening behavior was comparatively studied by adding 3 mm diameter polyethylene beads into the mixtures (6% by total volume). Natural flaw size distributions of composites without beads were determined by cross sectional analysis. The crack number and crack width distributions of specimens after flexural loading were characterized and the possible causes of changes in multiple cracking and deflection hardening behavior by flaw size distribution modification were discussed. Promising results from the view point of deflection hardening behavior were obtained from metakaolin incorporated and flaw size distribution modified PVA-ECCs prepared with W/B=0.53. The dual roles of W/B ratio and superplasticizer content on flaw size distribution, cracking potential and fiber-matrix bond behavior were evaluated. Flaw size distribution modification is found beneficial in terms of ductility improvement at an optimized W/B ratio.


