DOI: 10.11817/j.issn.1672-7207.2016.02.032

基于改进的非连续变形方法的洞室围岩稳定性分析

赵成龙¹，朱维申^{1, 2}，李术才^{1, 2}，虞松²

 (1. 山东大学 岩土与结构工程研究中心，山东 济南，250061；

2. 山东大学 土建与水利学院，山东 济南，250061)

摘 要：

工程，拓展非连续变形分析(DDA)的应用范围，将DDA中自带的平面应力问题转换为平面应变问题，对平面应变模型进行算法分析，并在VC++平台下程序实现；将岩体DDA方法平面应变模型应用于大型地下洞室开挖，并将模拟结果与已有大型洞室的物理实验结果进行对比。研究结果表明：DDA方法中平面应力模型的改进可行，与物理试验结果吻合度较好；洞室围岩的破坏与开挖的关系密切；DDA方法平面应变模型应用于大型地下工程，可以更好地分析洞室围岩的稳定性。

关键词：

DDA；平面应变模型；程序编制；洞室开挖；模拟试验；

中图分类号：TU443             文献标志码：A         文章编号：1672-7207(2016)02-0593-06

Stability analysis of cavern’s surrounding rock mass by improved discontinuous deformation analysis method

ZHAO Chenglong¹, ZHU Weishen^{1, 2}, LI Shucai^{1, 2}, YU Song²

(1. Geotechnical and Structural Engineering Research Center, Shandong University, Jinan 250061, China;

2. School of Civil and Hydraulic Engineering, Shandong University, Jinan 250061, China)

Abstract: In order to reflect the real rock engineering and expand the application range of discontinuous deformation analysis (DDA), the plane strain problem was considered, and its algorithm was analyzed and programmed based on VC++ platform. The plane strain model was applied to analyze the cavern excavation for large underground engineering. The results show that the algorithm of DDA is feasible and consistent with the results of laboratory tests well, and surrounding rock masses’ failure is related with the excavation process to a large degree. DDA plane strain model can be used to analyze the stability of cavern’s surrounding rock masses well.

Key words: DDA; plane strain model; programming; cavern excavation; simulation test

非连续变形分析(DDA)方法^[1]是一种新型数值分析方法，由于块体在计算过程的相对独立性，非连续类数值方法求算任意大位移问题在数学上不会遇到困难^[2-4]。它在满足弹性理论基本方程条件下解决了岩体的大变形和大位移问题, 既具有有限元理论基础的严密性，又具有离散元法可计算块体大位移的特点。DDA以位移作基本未知量, 主要适用于不连续块体系统。DDA方法研究的更多成果用在实际问题上，进行岩体非连续变形特征和破坏机制分析^[5-7]。目前，DDA理论已经取得了较大进展^[8-11]。马永政等^[12]在DDA程序中引进无网格节点位移插值模式；姜清辉 等^[13]对DDA采用的常加速度法进行拓展，给出求解块体系统运动方程的Newmark积分格式，并引入一种自适应阻尼，以保证求解的稳定性；高亚楠等^[14]采用有限变形理论对现有的DDA程序进行了改进；邬爱清等^[15]通过DDA高阶全多项式位移函数条件下的弹性力学推导，提出了一个逼近弹性力学连续位移函数真解的全多项式位移函数逼近方法。DDA方法本身考虑了岩体线弹性问题的平面应力问题，但是，由于隧道、大坝等地下洞室工程，在长轴方向上受结构的限制不可能产生应变，因此，通常用平面应变问题简化原有的计算，分析洞周围岩的应力和位移^[16]。本文作者将DDA中自带的平面应力问题转换为平面应变问题，拓展DDA的应用范围，以便更好地进行岩土工程稳定性分析，并与已有物理试验结果进行比较验证。

1  DDA理论

1.1  总体平衡方程

DDA方法中建立的总体平衡方程为

       (1)

其中：k_ii和k_ij为6×6的子阵；D_i和F_i分别为第i个块体的变形量子矩阵和荷载子矩阵，都是6×1子阵，

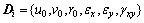          (2)

u₀和v₀为块体内指定点(x₀，y₀)的刚体位移；r₀为以指定点(x₀，y₀)为转动中心的转角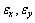；和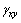分别为块体的正应变和剪应变。

1.2  块体位移

平衡方程求解后，可求得块体的D_i，从而块体中任意点的位移为

                (3)

式中：位移转换矩阵

 (4)

1.3  平面应变模型

弹性力学的平面问题包括平面应力问题和平面应变问题。2种平面问题的物理方程是不一样的。平面应力问题的物理方程为

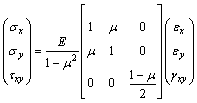      (5)

其中：E为弹性模量；μ为泊松比。将平面应力问题

的应力—应变关系中的弹性模量E换成，泊松比μ换成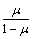，即可得平面应变问题的物理方程为

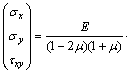
     (6)

式(6)中的矩阵E_i可以扩展为1个6×6的矩阵：

 (7)

DDA中块体i的弹性应力所产生的应变能为

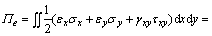
       (8)

其中：A为块体i的面积。

把对求极值得到的6个线性方程叠加到总体方程组中，得到平面应变条件下弹性应变能在平面应变条件下对总体方程的贡献：

2  算例验证

2.1  模型试验

朱维申等^[17]以1个大型水利工程为背景进行大型洞室围岩稳定性模型试验研究。图1所示为水电站附近的3组节理，为了简化，该模型试验只模拟N50^°E和N30^°W 方向2组节理。模型的几何比例尺为1:200，模型体的实际高×宽为1.7 m×1.6 m。计算域的外边界在垂直方向上，上、下各取为洞室最大高度的2倍以上, 水平方向则取洞宽的7倍以上。

采用先施加初始地应力而后开挖的加载方式。平面内的初始地应力为水平向σ_H=28.84 MPa，垂直向σ_V=13.35 MPa。主厂房自上而下分5步开挖。

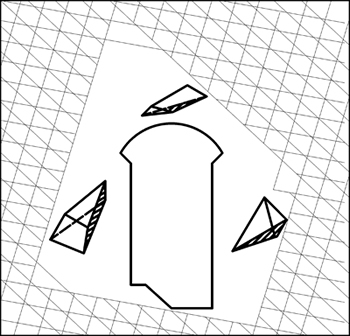
图1  水电站附近的节理

Fig. 1  Joint system around power house

在第1步至第3步的开挖过程中，洞室顶部围岩垂直方向和水平方向的位移均不明显，上下游两侧墙在垂直方向位移很小，在水平方向产生了向洞室内的位移，但其值很小。第4步开挖开始至第5步开挖完毕，洞室的顶部围岩向岩体内产生明显的垂直方向位移，最大位移约为0.1 cm。洞室两侧墙围岩则产生向洞室内的水平位移，最大位移量右侧壁约为0.3 cm，左侧壁约0.25 cm，其部位均在侧墙壁的中点，围岩位移曲线如图2所示。

在第1步至第3步的开挖过程中，厂房围岩基本不发生破坏，仅在第2步开挖时，顶部围岩中由两组节理和顶部临空面形成小三角岩块的崩落。由第4步开挖开始至第5步开挖完毕，下游侧墙出现沿2组节理与侧墙临空面形成的倒三角滑动岩体。上游侧墙围岩出现沿陡倾角节理面向洞内倾倒，沿缓倾角节理面向洞室内结构块体滑坍。

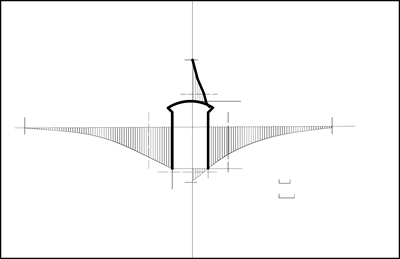
图2  围岩实验位移变化曲线

Fig. 2  Experimental displacement curve on downstream side wall surrounding rock

2.2  DDA数值模拟

2.2.1  模型建立

DDA计算模型如图3所示。洞室断面形式为圆拱直墙型，宽为0.200 m，左下游边墙垂直距离为0.255 m，底板到顶拱垂直距离为0.340 m。2组节理相互切割形成矩形块体单元，切割块体单元长×宽为 0.040 m×0.025 m。在一般情况下，洞室群厂房变形最大的位置位于洞室围岩中部位置，为了研究围岩深度和位移量的关系，在上、下游边墙中部位置各取1个监测断面。洞室的顶拱及上、下游边墙位移监测点布置如图4所示。

2.2.2  初始应力及力学参数

采用先施加初始地应力而后开挖的加载方式。初始地应力为水平向σ_L=-14.42 kPa，σ_L=14.42 kPa垂直向σ_H=-6.675 kPa。岩石力学参数如表1所示。

图3  DDA计算模型

Fig. 3  DDA computational model

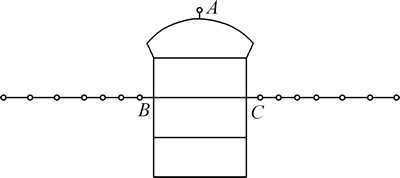
图4  测点布置图

Fig. 4  Measuring point layout diagram

表1  洞室岩体和节理的力学参数

Table 1  Mechanical parameters of rock mass and joints

2.2.3  开挖顺序

与洞室实际开挖顺序及实验相同，该主厂房洞室分5步开挖，开挖模式如图5所示。

图5  开挖模式示意图

Fig. 5  Excavation model diagram

2.3  结果对比

2.3.1  洞周围岩不同位置位移分析

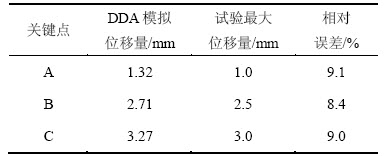
表2所示为地下洞室围岩关键点位移。由表2可知：开挖完成后，拱顶模拟最大位移为1.091 mm，试验最大位移为1.000 mm，相对误差为9.1%；上游边墙模拟最大位移为2.710 mm，试验值为2.500 mm，相对误差为8.4%；下游边墙模拟最大位移为3.270 mm，试验值为3.000 mm，相对误差为9.0%。

模拟位移与实验值相比偏大，说明把三维实验简化为二维问题进行数值模拟是有差异的。但是，拱顶及上下游边墙位移相对误差都在10%以内，说明这种位移预测方法可行，对实际工程有一定指导意义。上、下游边墙最大位移是拱顶位移的2倍多，此差异说明水平地应力较大。因此，在施工中，应重点加强对上下游边墙支护。

表2  地下洞室围岩关键点位移

Table 2  Key points’ displacements of underground cavern surrounding rock

2.3.2  上下游边墙围岩深度对位移的影响

图6和图7所示分别为上、下游边墙监测断面各测点位移量计算值与实验值对比曲线。从图6和图7可以看出：越靠近开挖洞室，上下游边墙向洞室内位移越大，远离洞室，围岩趋于稳定，位移变化不大，这与物理实验的位移变化趋势基本吻合。因此，在施工中，应适当加强开挖洞室附近的围岩支护。

2.3.3  洞室开挖的围岩破坏研究

洞室分步开挖过程如图8所示，图中圆圈的部位是掉块部位。

图6  上游边墙位移量计算值与实验值对比曲线

Fig. 6  Contrast curve of upstream wall displacement calculation value and experimental value

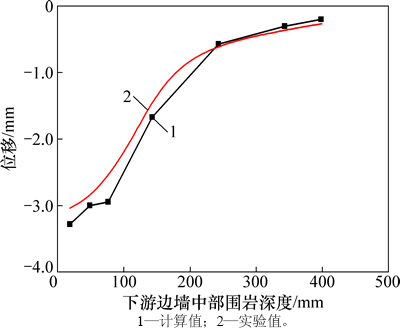
图7  下游边墙位移量计算值与实验值对比曲线

Fig. 7  Contrast curve of downstream wall displacement calculation value and experimental value

图8  DDA洞室的开挖过程

Fig. 8  Excavation processes of cavern

从图8可以看出：围岩的破坏与开挖的关系密切；开挖上部台阶时，围岩较为稳定；开挖下部台阶时，围岩变形较大；第1步开挖时，围岩较稳定，变形不大；第2步开挖时，拱顶靠近中部位置临空面有小的类三角岩块崩落；第3步开挖时，拱顶左肩无明显岩块掉落，拱顶右肩有小的岩块崩落，但是，总体来看，第1步至第3步开挖过程洞室围岩基本没有发生破坏。

第4步至第5步开挖时，上游侧墙出现沿节理面向洞室内滑塌的岩块，下游侧墙沿侧墙出现向临空面倾倒的块体，而且下游侧墙明显比上游侧墙坍塌得厉害。图8中圆圈部位是施工不稳定的地方，上下游侧墙明显比拱顶部位坍塌的厉害，因此，在施工中，尤其要加强上下游两侧边墙的支护。以上开挖围岩破坏的发展趋势与试验趋势基本一致。

3  结论

1) 通过物理试验和数值计算发现，在第1至第3步开挖过程中，洞室围岩基本处于稳定状态；第4步开挖至第5步开挖，洞室围岩产生了明显的不稳定现象，且两侧墙的围岩变形大于拱顶的围岩变形；离洞室越近，开挖临空效应越明显，围岩产生了较大变形和位移，稳定性变差。

2) 通过VC++平台，实现了平面应变模型在岩石破坏非连续变形分析中的应用，模拟结果和已有的物理实验结果吻合得较好，表明本文对DDA模型的改进合理、有效。

参考文献：

[1] SHI G H. Discontinuous deformation analysis: a new numerical model for the statics and dynamics of block system[D]. Berkeley: University of California. Department of Civil Engineering, 1988: 3-52.

[2] LIN C T, AMADEI B, JUNG J, et al. Extensions of discontinuous deformation analysis for jointed rock mass[J]. International Journal of Rock Mechanics and Mining Sciences& Geomechanics Abstracts, 1996, 33(1): 671-694.

[3] SHI G H. Block system modeling by discontinuous deformation analysis[M]. Southampton UK and Boston USA: Computational Mechanics Publications, 1993: 1-49.

[4] 裴觉民, 石根华. 岩石滑坡体的块体动态稳定和非连续变形分析[J]. 水利学报, 1993, 12(3): 28-34.

PEI Juemin, SHI Genhua. Block dynamic stability and discontinuous deformation analysis[J]. Journal of Hydraulic Engineering, 1993, 12(3): 28-34.

[5] WANG C Y, CHANG C T, SHENG J. Time integration theories for the DDA method with finite element Meshes[C]//Proceedings of the First International Forum on Discontinuous Deformation Analysis(DDA) and Simulations of Discontinuous Media. Albuquerque: TSI Press, 1996: 263-288.

[6] 张国新, 武晓峰. 裂隙渗流对岩石边坡稳定性的影响-渗流、变形耦合作用DDA法[J]. 岩石力学与工程学报, 2003, 22(8): 1269-1275.

ZHANG Guoxin, WU Xiaofeng. Influence of seepage on the stability of rock slope-coupling of seepage and deformation by DDA method[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(8): 1269-1275.

[7] LIN C T, AMADEI B, JUNG J, et al. Extensions of discontinuous deformation analysis for jointed rock masses[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1996, 33(7): 671-694.

[8] 黎勇, 冯夏庭, 栾茂田, 等. 非连续变形计算力学模型中的接触力元[J]. 东北大学学报(自然科学版), 2002, 23(11): 1112-1115.

LI Yong, FENG Xiating, LUAN Maotian, et al. Contact force element of discontinuous deformation computational mechanics model[J]. Journal of Northeastern University (Natural Science), 2002, 23(11): 1112-1115.

[9] 姜清辉. 三维非连续变形分析方法的研究[D]. 武汉: 中国科学院武汉岩土力学研究所, 2000: 69-118.

JIANG Qinghui. Research on three-dimensional discontinuous deformation analysis method[D]. Wuhan: Institute of Rock and Soil Mechanics. Chinese Academy of Sciences, 2000: 69-118.

[10] 何传永, 孙平, 吴永平, 等. 用DDA 方法验证倾倒边坡变形的制动机制[J]. 中国水利水电科学研究院学报, 2013, 11(2): 107-111.

HE Chuanyong, SUN Ping, WU Yongping, et al. Discussion on the deformation mechanism of topple rock slope using DDA method[J]. Journal of China Institute of Water Resources and Hydropower Research, 2013, 11(2): 107-111.

[11] 冯细霞, 邬爱清, 卢波. DDA 块体接触开-闭迭代研究[J]. 长江科学院院报, 2014, 31(4): 52-58.

FENG Xixia, WU Aiqing, LU Bo. Open-close iterations for DDA contacts[J]. Journal of Yangtze River Scientific Research Institute, 2014, 31(4): 52-58.

[12] 马永政, 郑宏, 李春光. 应用自然邻接点插值法的块体非连续变形分析[J]. 岩土力学, 2008, 29(1): 119-124.

MA Yongzheng, ZHENG Hong, LI Chunguang. Applying natural neighbor interpolation to discontinuous deformation analysis of block system[J]. Rock and Soil Mechanics, 2008, 29(1): 119-124.

[13] 姜清辉, 周创兵, 漆祖芳. 基于Newmark积分方案的DDA 方法[J]. 岩石力学与工程学报, 2009, 28(1): 2778-2783.

JIANG Qinghui, ZHOU Chuangbin, QI Zufang. Discontinuous deformation analysis method based on Newmark integration algorithm[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(1): 2778-2783.

[14] 高亚楠, 高峰, YEUNG M R. 基于有限变形理论的非连续变形分析方法改进[J]. 岩石力学与工程学报, 2011, 30(11): 2360-2365.

GAO Yanan, GAO Feng, YEUNG M R. Modification of discontinuous deformation analysis method based on finite deformation theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(11): 2360-2365.

[15] 邬爱清, 刘晓莹, 张杨, 等. 基于DDA的弹性力学全高阶多项式位移逼近方法及其实例验证[J]. 固体力学学报, 2014, 35(2): 142-149.

WU Aiqing, LIU Xiaoying, ZHANG Yang, et al. A DDA based complete and high order polynomial displacement approximation method in elastic mechanics and its cases verification[J]. Chinese Journal of Solid Mechanics, 2014, 35(2): 142-149.

[16] 沈明荣. 岩体力学[M]. 上海: 同济大学出版社, 1999: 45-94.

SHEN Mingrong. Rock mechanics[M]. Shanghai: Tongji University Press, 1999: 45-94.

[17] 朱维申, 何满潮. 复杂条件下围岩稳定性与岩体动态施工力学[M]. 北京: 科学出版社, 1996: 51-55.

ZHU Weishen, HE Manchao. stability of surrounding rock under complicated conditions and dynamic construction mechanics of rock masses[M]. Beijing: Science Press, 1996: 51-55.

(编辑  罗金花)

收稿日期：2015-02-20；修回日期：2015-04-20

基金项目(Foundation item)：国家自然科学基金重点资助项目(51139004，41072234)；教育部博士点基金资助项目(20110131110030)；山东省自然科学基金资助项目(ZR2011EL049)(Projects (51139004, 41072234) supported by the National Natural Science Foundation of China; Project (20110131110030) supported by the Research Fund for the Doctoral Program of Higher Education of China; Project (ZR2011EL049) supported by the Natural Science Foundation of Shangdong Province)

通信作者：李术才，教授，博士生导师，从事岩石断裂损伤和岩石稳定性分析研究；E-mail：lishucai@sdu.edu.cn

摘要：为了更符合实际工程，拓展非连续变形分析(DDA)的应用范围，将DDA中自带的平面应力问题转换为平面应变问题，对平面应变模型进行算法分析，并在VC++平台下程序实现；将岩体DDA方法平面应变模型应用于大型地下洞室开挖，并将模拟结果与已有大型洞室的物理实验结果进行对比。研究结果表明：DDA方法中平面应力模型的改进可行，与物理试验结果吻合度较好；洞室围岩的破坏与开挖的关系密切；DDA方法平面应变模型应用于大型地下工程，可以更好地分析洞室围岩的稳定性。