Relationship between partial and average atomic volumes of components in Au-Ni alloys
XIE You-qing1, 2
1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;
2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China
Received 25 August 2010; accepted 28 November 2010
Abstract: In the framework of systematic science of alloys, the average molar property (volume and potential energy) functions of disordered alloys were established. From these functions, the average molar property functions, partial molar property functions, derivative functions with respect to composition, general equation of relationship between partial and average molar properties of components, difference equation and constraining equation of different values between partial and average molar properties, as well as general Gibbs-Duhem formula were derived. It was proved that the partial molar properties calculated from various combinative functions of average molar properties of alloys are equal, but in general, the partial molar properties are not equal to the average molar properties of a given component. This means that the partial molar properties cannot represent the corresponding properties of the component. All the equations and functions established in this work were proved to be correct by calculating the results of partial and average atomic volumes of components as well as average atomic volumes of alloys in the Au-Ni system.
Key words: systematic science of alloys; partial molar volume; average atomic volume; Au-Ni system
1 Introduction
In the traditional thermodynamics of alloys, the average properties of components cannot be obtained by separating the total Q-function of the alloys, therefore, the average Q-property of components α is represented by the partial molar property 
. In the framework of systematic science of alloys [1-8], the average energy E-functions and average volume V-functions of alloys are formed respectively by adding average energy 
-functions and adding average volume 
-functions of components α (α=A, B). It means that the average properties 
(Q=E, V) of components can be obtained by separating the total Q-function of the alloys. In this study, the relationship functions between the average and partial molar properties were established. Taking volume property of Au-Ni system as an example, it was proved that in general the partial molar properties cannot represent the corresponding properties of the component.
2 Relationship between average and partial molar properties of components
In the framework of systematic science of alloys, the molar property of solid solution Qm is described by the combinative function of average molar property functions 
and 
of components A and B:
(1)
where xA and xB are the mole fractions of components A and B, respectively.
In the traditional thermodynamics of alloys, the average molar properties and of components A and B cannot be obtained by separating the molar properties of the solid solution, therefore, the average molar properties and of components A and B are represented respectively by partial molar properties 
and 
, and the definition of which is [9]
(2)
where Q is the total property of the solid solution; nA and
nB are the mole numbers of components A and B, respectively; T is temperature and P is pressure.
In this case, the total property Q of the solid solution can be described by the assembling function of partial molar property functions:
(3)
and
(4)
For Eq. (2), the partial derivative of Q with respect to nA (or nB) can be changed to Q with respect to xA (or xB):
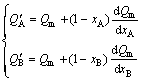(5)
Substituting Eq. (1) into Eq. (5), the general equation of relationship between partial and average molar properties of components can be obtained:
(6)
From the above equations, the following conclusions can be arrived.
1) From Eq. (5), it is known that the partial molar properties depend on the results of combinative functions of the solid solution, not on the average molar property functions of components A and B. This means that if various combinative functions have the same curves of the molar property of the solid solution as a function of composition, the partial molar properties obtained from the various combinative functions are the same, although their average molar property functions of components A and B may be obviously different.
2) From Eq. (6), it can be proved that the combinative function is identically equal to the assembling function:
(7)
and
so,
(8)
3) From Eq. (6), the difference equation between partial and average molar properties, and the constraining equation of difference values between partial and average molar properties of components A and B can be obtained:
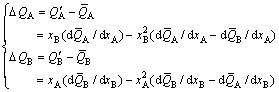(9)
(10)
The constraining equation of difference values Eq. (10) can be used to check the calculated results.
4) From Eq. (6), the general Gibbs-Duhem can be derived:
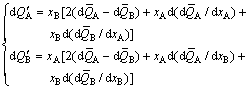(11)
(12)
5) From Eq. (6), the condition for the partial molar properties equal to the average molar properties of components A and B can be obtained:
(13)
or
(14)
3 Energy and volume functions of disordered alloys
According to the characteristic atoms arranging (CAA) model and characteristic crystals (CCM) mixing model, three kinds of average molar properties functions of components A and B for disordered alloys were established [1-8].
I-type:
(15)
II-type:
(16)
III- type:
(17)
where I is the coordination number,
and 
denote respectively atomic potential energies (
and 
) and volumes (
and 
) of primary characteristic atoms, or molar potential energies (
and 
) and molar volumes (
and 
) of primary characteristic crystals, as well as 
and 
denote respectively atomic potential energies (and ) and atomic volumes (and ) of the terminal characteristic atoms, or molar potential energies (and ) and molar volumes (and ) of terminal characteristic crystals; I=12, for FCC-solid solution.
By combining Eqs. (15), (16) and (17) and substituting them into Eq. (1), the nine combinative functions of average atomic/molar properties of the disordered alloys can be obtained (see Table 1). The derivative equations and functions of partial molar properties obtained from these combinative functions are respectively listed in Tables 2 and 3.
4 Atomic volumes of Au-Ni alloys
The Au-Ni system is a face center cubic (FCC) continuous solid solution [10-11]. According to the experimental values of lattice constants of pure Au- and Ni-metals, as well as Au(1-x)Nix alloys [12], the atomic volumes
and
of primary characteristic atoms and the atomic volumes
and 
of terminal characteristic atoms in the average atomic volume functions are obtained as listed in Table 4.
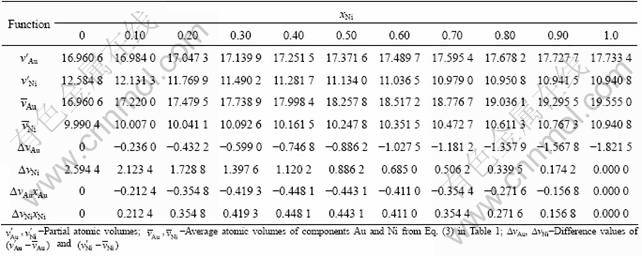
According to the parameters in Table 4, the results calculated by functions above are listed in Tables 5 and 6. From these results, the following knowledge is obtained.
1) The calculated values (Vcal) of average atomic volumes of Au(1-x)Nix alloys obtained from Eqs. (2)-(9) in Table 1 are equal to each other and in good agreement with the experimental atomic volumes (vexp). It means that Eqs. (2)-(9) in Table 1 can be used to calculate the average atomic volumes of Au(1-x)Nix alloys, if the average atomic volumes of components Au and Ni in the Au(1-x)Nix alloys is not needed.
2) The values (v′Au and v′Ni) of partial atomic volumes of components Au and Ni in the Au(1-x)Nix alloys obtained from Eqs. (2)-(9) in Table 1 are equal to each other, because the compositional dependences of average atomic volumes of Au(1-x)Nix alloys described by Eqs. (2)-(9) are the same.
3) The calculated values of average atomic volumes of components Au and Ni in the Au(1-x)Nix alloys obtained from Eqs. (2)-(9) in Table 1 are different from each other. This means that it is not an easy problem to determine components Au and Ni on the contribution to the volume of alloys, or to choose the volume function in Table 1 for Au-Ni system. This difficult problem was resolved for Au-Cu [13-15], Ag-Cu and Ti-Al systems through the study of volume and energy functions associated with electronic structures of alloys.
4) The difference values between partial and average atomic volume obtained from function 3 in Table 1 are the greatest. But these difference values obey the constraining equation 
. It is also proved that .
Table 1 Average property functions of disordered binary alloys (Q=E or V)
Table 2 Derivative equations of average property functions of disordered binary alloys (Q=E or V)
Table 3 Functions of partial molar (or partial atomic) properties of components for disordered binary alloys(Q=E or V)
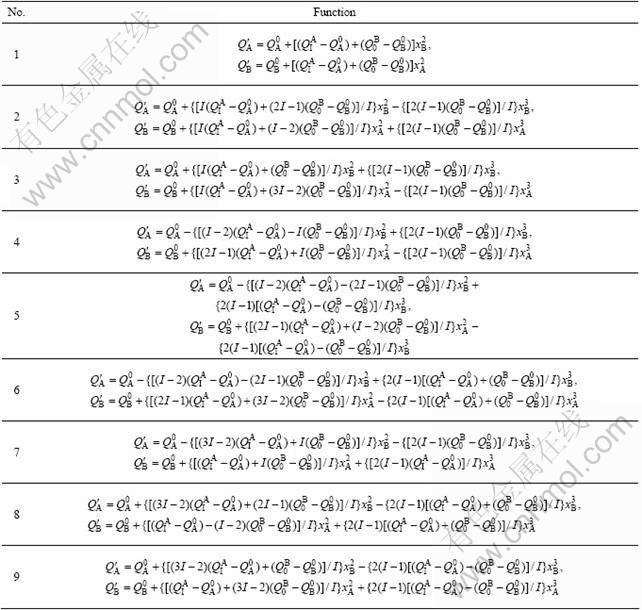
Table 4 Atomic volumes
, 
and 
in average volume functions of Au-Ni system
Table 5 Partial atomic volumes and average atomic volumes of Au-Ni system (a in 10-1nm; v in 10-3nm3)
Table 6 Atomic volumes of Au-Ni system obtained from Eq. (3) (v in 10-3nm3)
5 Conclusions
1) In the framework of systematic science of alloys, the energy and volume properties of alloys are described by combinative functions, from which the average molar/atomic properties of components can be obtained.
2) It is proved that the partial molar/atomic property cannot represent the average molar/atomic property of the component.
3) For a given alloy system, the energy and volume functions can be chosen through the study of volume and energy properties associated with electronic structures of alloys.
References
[1] XIE You-qing. Atomic energies and Gibbs energy functions of Ag-Cu alloys [J]. Science in China (Series E), 1998, 41(2): 146-156.
[2] XIE You-qing, ZHANG Xiao-dong. Atomic volumes and volumes functions of Ag-Cu alloys [J]. Science in China (Series E), 1998, 41(2): 157-168.
[3] XIE You-qing, ZHANG Xiao-dong. Electronic structure of Ag-Cu alloys [J]. Science in China (Series E), 1998, 41(3): 225-236.
[4] XIE You-qing, ZHANG Xiao-dong. Phase diagram and thermodynamic properties of Ag-Cu alloys [J]. Science in China (Series E), 1998, 41(4): 348-356.
[5] XIE You-qing, TAO Hui-jing, PENG Hong-jian, LI Xiao-bo, LIU Xin-bi, PENG KUN. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC TiAl2 type alloys [J]. Physica B, 2005, 366: 17-37.
[6] XIE You-qing, PENG Hong-jian, LIU Xin-bi, PENG KUN. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC Ti3Al-type alloys [J]. Physica B, 2005, 362: 1-17.
[7] XIE You-qing, LIU Xin-bi, PENG KUN, PENG Hong-jian. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC TiAl3-type alloys [J]. Physica B, 2004, 353: 15-33.
[8] XIE You-qing, PENG KUN, LIU Xin-bi. Influences of xTi/xAl on atomic states, lattice constants and potential energy planes of ordered FCC TiAl-type alloys [J]. Physica B, 2004, 344: 5-20.
[9] WALTER J M. Physical chemistry [M]. 5th Edition. London: Longman Group Limited, 1976: 229.
[10] WANG J, LU X G., SUNDMAN B, SU X, Thermodynamic assessment of the Au-Ni system [J]. CALPHAD, 2005, 29(4): 263-268.
[11] TOMISKA J, ERDELYI L, NECKEL A. Mass-spectrometric determination of thermodynamic activities of liquid alloy system Au-Ni and calculation of phase-diagram [J]. Metallk Z, 1977, 68: 734-739.
[12] PEARSON W B. Handbook of lattice spacings and structures of metals and alloys [M]. London: Pergamon, 1958.
[13] XIE You-qing, LI Yan-fen, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang. Systematic science of Au-Cu system based on experimental data of disordered alloys: Characteristic atom occupation patterns of Au3Cu, AuCu3, AuCu I and AuCu II [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(5): 1092-1104.
[14] XIE You-qing, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang. Volume sequences of characteristic atoms separated from experimental volumes of AuCu and AuCu3 compounds [J]. Transactions of Nonferrous Metals Society of China, 2009, 19(6): 1599-1617.
[15] XIE You-qing, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang. Potential energy sequences of characteristic atoms on basis of experimental heats of formation of AuCu and AuCu3 compounds (I) [J]. Transactions of Nonferrous Metals Society of China, 2009, 19(5): 1243-1256.
Au-Ni合金中组元的平均原子体积和偏摩尔体积的关系
谢佑卿1, 2
1. 中南大学 材料科学与工程学院，长沙 410083；
2. 中南大学 粉末冶金国家重点实验室，长沙 410083
摘 要：
在系统合金科学框架中建立有关无序合金的平均摩尔性质(体积和势能)的函数。通过对这些函数进行推导，可以得到平均摩尔体积函数、偏摩尔体积函数及派生出与成分相关的函数。在组元的偏摩尔性质和平均摩尔性质之间的普适方程、差分方程、在偏摩尔性质和平均摩尔性质之间不同参数的约束方程和普适的Gibbs-Duhem公式。可以证明从合金平均摩尔性质的不同函数计算的偏摩尔性质是相等的，但总体来说偏摩尔性质不等于给定组元的平均摩尔性质，即偏摩尔性质不能代表相应组元的摩尔性质。通过计算Au-Ni系中组元的偏摩尔体积和平均原子体积以及合金的平均原子体积，证明所建立的公式和函数的正确性。
关键词：
系统合金科学; 偏摩尔体积; 平均原子体积; Au-Ni系；
(Edited by FANG Jing-hua)
Foundation item: Project (51071181) supported by the National Natural Science Foundation of China; Project (2010FJ4034) supported by Natural Science Foundation of Hunan Province, China
Corresponding author: XIE You-qing; Tel: +86-731-88879287; E-mail: xieyouq2000@yahoo.com.cn
DOI: 10.1016/S1003-6326(11)60934-5
