Article ID: 1003-6326(2005)05-0997-06
Capillary wave formation on excited solder jet and fabrication of lead-free solder ball
ZHANG Shu-guang(张曙光), HE Li-jun(何礼君),
ZHU Xue-xin(朱学新), ZHANG Shao-ming(张少明),
SHI Li-kai(石力开), XU Jun(徐 骏)
(National Engineering Research Center for Nonferrous Metals Composites, General Research Institute for Nonferrous Metals, Beijing 100088, China)
Abstract:
A survey of solder ball production processes especially focusing on disturbed molten metal jet breakup process was made. Then the formation of capillary wave on tin melt jet in the way of rapid solidification was studied. A semi-empirical formula, which can be written as λ=Cvib(σ/ρ)1/3f-2/3 to predict the relationship between wavelength of capillary wave and frequency of imposed vibration was obtained. Sn-4.0Ag-0.5Cu lead free solder ball was successfully produced with tight distribution and good sphericity. The excited jet breakup process is promising for cost effectively producing solder ball.
Key words:
jet; breakup; capillary wave; disturbance; solder ball CLC number: TG425.1;
Document code: A
1 INTRODUCTION
As the electronic package technology drives towards high input/output (I/O) count and smaller packages with finer pitch, the leads are shifted from the periphery of the device to the area under the device. This scheme is called a real array packaging and is exemplified by the ball grid array(BGA) package. Solder balls used in these packages have severe specifications in diameter tolerance, roundness and surface quality, e.g., sphere size variation is required within ±3% from the mean sphere diameter to ensure a reliable package assembly, and this requirement is a challenge to conventional manufacturing methods for tiny metal balls[1].
There are many conventional processes used to produce solder balls. However, all have disadvantages in terms of low gaining or yield rate and are not economical. Gas atomization and centrifugal a wide atomization have the disadvantage of distribution in size, thus intensive classification is required. The sphericity of the solder balls made by the abovementioned atomization processes is also not perfect. Another process is cutting or stamping where a metal piece of uniform mass is cut from a solder wire or stamped from a solder foil. The solder pieces are introduced into a variable temperature oil bath where the pieces melt, spheroidize and solidify. The main shortcoming of the process is its low production rate and complicated procedures. Also, the process is not available to produce solder ball of materials with poor plastic deformation ability, e.g., bismuth-containing solder alloys, which is difficult to make small size solder wire or foil and thus the solder pieces of uniform mass.
The breakup of a liquid jet into discrete drops controlled by the application of a periodic disturbance to the jet has attracted considerable academic and industrial interest recently. This technology has been successfully used in the field of ink jet printing. In 1990s, Laboratory for Manufacturing and Productivity at Massachusetts Institute of Technology(MIT) led by Chun[2] first developed molten metal jet breakup process and termed UDS(Uniform droplet spray) process. Later, the application of UDS process for advanced material processing was studied, and soon many industrial applications including metal injection molding, hot isostatic pressing, BGA electronics packaging, net-shape spray deposition and rapid prototyping were offered[2, 3].
Recently, Orme et al[4-6] applied the process to direct writing technology and net-form manufacturing. Lee[7] studied liquid jet breakup and the formation of satellite droplet under the influence of different waveforms. Hitachi Metals Company have used this technology to manufacture solder ball[8].
In this paper, the production of solder ball by molten metal jet breakup process was mainly focused, the influences of processing parameters on the formation and growth of capillary wave of the jet were discussed, and the characteristics of Sn-4.0Ag-0.5Cu solder ball produced by this process were studied.
2 EXPERIMENTAL
The experimental apparatus comprises a crucible, a spray chamber, a gas control system, and a vibrator, as illustrated in Fig.1. The crucible, a pressurized liquid reservoir, has an orifice at the bottom and constrains molten metal controllable on its level. Immediately below the crucible and the orifice is the spray chamber, a sealed chamber capable of being evacuated and backfilled with protective gas to avoid the disruptive effects of oxidation, in which a coolant tank is located under the crucible. The gas control system creates an inert atmosphere in the spray chamber and forces the melt from the crucible and through the orifice to form a laminar jet. The vibrator is immersed in the molten metal of the crucible and serves to divide an issuing stream into droplets by imposing vibrations to the molten metal excited by a piezo-electric transducer.
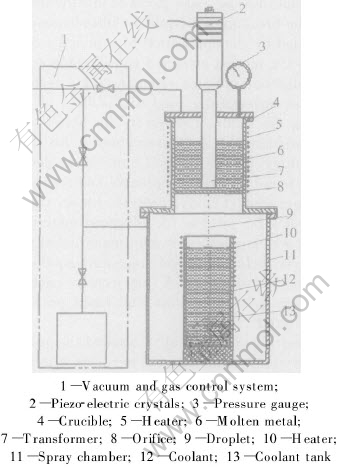
Fig.1 Schematic diagram of apparatus
The diameters of the orifices used in this work were 90μm and 180μm, respectively. The imposed vibration frequencies were 20.32, 4.79 and 2.94kHz, respectively. The spray chamber was evacuated and filled with nitrogen. Tin was melted to 560K, and then the continuous molten jet of tin was formed through the orifice with a velocity of 2m/s to 5m/s by applying nitrogen gas pressure typically 20kPa to 260kPa to the crucible. In order to observe the formation of capillary wave on molten metal jet, the coolant tank was filled with water to freeze the molten metal jet into a beaded jet before its breakup into droplets through adjusting the distance between the orifice and the water top level. The wavelength of capillary wave can be measured using the frozen beaded jet by image analyzer, and consequently, the influences of the orifice diameter and the vibration frequency on the capillary wavelength can be obtained.
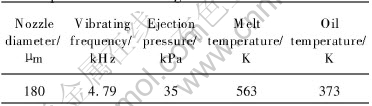
Solder balls can be produced by changing coolant from water to silicon oil in the coolant tank and adjusting the silicon oil temperature gradient. The process conditions used to produce Sn-4.0Ag-0.5Cu solder ball are listed in Table 1. The solder balls collected in the coolant tank were ultrasonically rinsed by acetone. The diameter distribution of the solder balls was analyzed by image analyzer, and the morphology of which was observed by scanning electronic microscopy(SEM).
Table 1 Process conditions used to produce Sn-4.0Ag-0.5Cu solder balls
3 RESULTS AND DISCUSSION
3.1 Capillary wave formation
Fig.2(a) shows the jet morphology photographed by image analyzer at orifice diameter of 90μm and no imposed vibration. Fig.2(b) shows the jet morphology at orifice diameter of 90μm and vibration frequency of 20.32kHz, the formation of sinusoidal capillary wave on the jet can be clearly observed. However, compared with Fig.2(b), the capillary wave doesnt appear on the jet with the orifice diameter of 180μm when the other experimental conditions are kept the same, as shown in Fig.2(c). When the vibration frequency shifts from 20.32kHz to 4.79kHz and the other experimental conditions are the same as above, the results are shown in Fig.3. Sinusoidal capillary wave on the jet can be clearly seen in both Fig.3(b) and Fig.3(c) for different orifice diameters. The case under vibrating frequency 2.94kHz is also the same as shown in Fig.3.
As can be seen clearly from the research results, the formation of the capillary wave depends on the relationship of the orifice diameter and imposed vibration frequency. The capillary wave can emerge on the jet surface for certain vibration frequency with different orifice diameters, as shown in Fig.3, or the capillary wave can not emerge as shown in Fig.2(c). Therefore, the first problem needs to be resolved is how to select the proper vibration frequency for certain orifice diameter in order to make the capillary wave form on the jet and breakup into droplets.

Fig.2 Jet morphologies at vibration frequency(f) and orifice diameter(d)
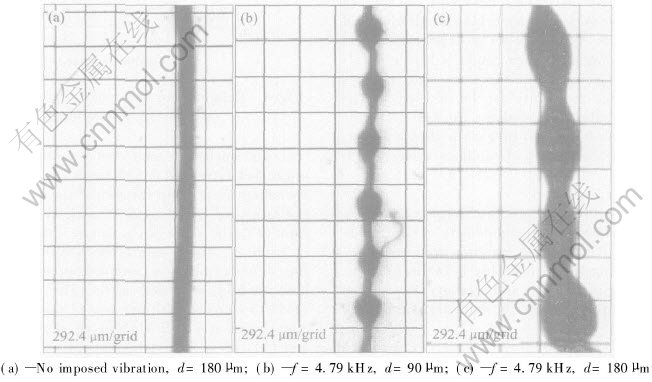
Fig.3 Jet morphologies at vibration frequency(f) and orifice diameter(d)
The study of liquid jets has a long and rich history. Rayleigh provided the foundation for breakup of liquid jets[9]. He developed the first linear stability analysis where he considered an infinitely long, circular, inviscid jet subject to a temporal disturbance growth. He found that disturbances of the radius grow exponentially with time and sinusoidally with space. The radial disturbance on the surface of the issuing jet will be unstable and grow resulting in droplet formation when the non-dimensional wave number β is less than unity, where β is defined as the ratio of the initial stream circumference to the wavelength of the imposed disturbance. In 1931, Weber[10] included aerodynamic terms to the theory proposed by Rayleigh. The inclusion of aerodynamic terms predicted the experimentally observed shorter stream breakup. The growth factors of inviscid flow were calculated by an energy method, the maximum growth rate occurs when the dimensionless wavelength (λm/dj) is 4.508 by Rayleighs analysis or 4.443 by Webers analysis for inviscid flow, where λm is the optimum capillary wavelength, and dj is the jet diameter. More detailed descriptions of the droplet formation process from capillary stream breakup can be found in the review articles by Bogy[11] and McCarthy[12]. In brevity, Lord Rayleighs study showed that if 0〈β〈1, i.e. the applied disturbance is chosen with its wavelength greater than the stream circumference, the capillary waves will become unstable and grow exponentially in time as e β t, ultimately resulting in droplet formation. Recently, Orme[13] showed that the most uniform droplet stream is the one that is perturbed with a disturbance whose frequency associated with the maximum β.
The mechanism of the relationship of capillary wave characteristics and perturbing conditions still remains unclear, however, lot of experimental and modeling studies have been conducted on it. Gallego-Juarez[14] pointed out the term that involves acceleration due to gravity can be omitted, if the frequency of vibration is above 10kHz. In this case, σ is about 0.1N/m, he got the threshold amplitude for the generation of capillary waves which is given by
δmo=2η[1/(πσρf2)]1/3(1)
where δmo is threshold amplitude; η, σ and ρ are viscosity, surface tension and density of the liquid, respectively; f is imposed vibrating frequency.
Considering the relationship between frequencies of driving oscillations and capillary waves, one can get the expression for the capillary wavelength λ
λ=[8πσ/(ρf2)]1/3(2)
Forrest[15] studied the modeling Faraday excitation of a viscous fluid, and got the predictions for the scaling between excitation wavelength and exciting frequency. For liquids with low non-dimensional wave number (corresponds to ultrasound frequency below 40kHz) the scaling between excitation wave number, k(k=2π/λ), and the exciting frequency, f, was determined to be
k=0.62616(σ/ρ)-1/3f2/3(3)
According to the exciting frequency and melt characteristics used in this experiment, and by combination with Eqns.(2) and (3) after substituting k=2π/λ into Eqn.(3) , the expression for the scaling between excitation wavelength and exciting frequency can be written as
λ=Cvib(σ/ρ)1/3f-2/3(4)
where Cvib is the value of imposed vibration coefficient.
By comparison of the research results of Eisenmenger, Forrest, MIT and this work, as shown in Fig.4, It can be concluded that the scaling between excitation wavelength and exciting frequency in molten metal jet breakup process is similar to that in ordinary medium jet breakup process predicted by Eisenmenger and Forrest, and the value of capillary wavelength locates closer to that predicted by Eisenmenger.
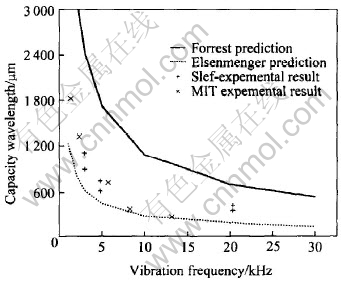
Fig.4 Relationship between vibrating frequency and capillary wavelength
The surface tension and density of liquid tin are 0.544N/m and 7000kg/m3[3], respectively. By substituting these values and the mean values of the measured wavelength λ(listed in Table 2) into Eqn.(4), the value of Cvib can be obtained as listed in Table 2. Also it can be seen from Table 2 and Fig.4, the capillary wavelength increases as the vibration frequency decreases. The value of Cvib tends to increase with increase of the vibrating frequency and the orifice diameter. From Eqns.(3) and (4), it can be gotten that the values of Cvib are 2.9 and 10, respectively. According to the experimental results of tin melt jet breakup process obtained by MIT and this work, the value of Cvib ranges from 3 to 7. So, it seems that the value of Cvib for molten metal ranges from 2.9 to 10 being located near the lower limit.
Generally, the issuing jet diameter is a little less than the orifice diameter, as shown in Table 2, due to the action of the surface tension. According to Rayleighs study, the jet is unstable to disturbances (axisymmetric) when the wavelength of the disturbance is greater than the circumference of the issuing jet. As can be seen from Table 2, the capillary wavelength is 365μm at vibration frequency of 20.32kHz and orifice diameter of 90μm and is larger than the circumference of 83μm in diameter jet but less than that of 159μm in diameter jet, and thus it makes the difference between Fig.2(b) and Fig.2(c). The capillary wavelength at vibrating frequency 4.79kHz is obviously larger than both the circumferences of 83μm and 159μm in diameter jets, and thus the sinusoidal capillary waves emerge in both cases. So does the case at vibrating frequency of 2.94kHz.
Therefore, Eqn.(4) can be simply used, though not very accurately, to predict the formation of the capillary wave under the selected frequency (generally bellow 40kHz) of imposed vibration for certain orifice diameter in order to ensure the breakup of molten metal jet into droplets.
3.2 Fabrication of lead-free solder balls
On the basis of the above experimental results, Sn-4.0Ag-0.5Cu solder ball with good sphericity and narrow distribution was produced by controlling the breakup of a continuous laminar jet into uniform droplets and then by slowly solidifying the droplets in the coolant tank filled with silicone oil, as shown in Fig.5 and Fig.6.
As the solder balls have not been precisely classified, there are some egg-like particles shown in Fig.5. The processing parameters, especially temperature gradient of the coolant, need further optimizing. Fig.6 shows the size distribution of three hundred balls picked up randomly from one of the batches. About 60 percent of the solder balls ranges between the narrow distribution of 3% of mean diameter of 280μm with a standard deviation of 10μm. A second peak appears near the diameter of 380μm in Fig.6. Taking into account two solder balls of the same size merging into a single one, the diameter of the new one is 1.26 times, i.e. 21/3 times that of the former. Though 380μm is 1.36 times the mean diameter of 280μm, a little more than the calculated value, we still ascribe the existence of the second peak in diameter distribution to the agglomeration of two droplets. The difference between the calculated and experimental values may result from imperfect roundness, not exactly the same size of the droplets and analysis error caused by the image instrument. The spheroidization process of the coalesced particle having not completed, exhibiting the incompleted form of dumbbell or snowman, is shown in Fig.7.

Fig.5 SEM photographs of Sn-4.0Ag-0.5Cu solder balls made by melt jet breakup process
Table 2 Imposed vibration coefficient and capillary wavelength values for
different orifice diameter and vibrating frequency

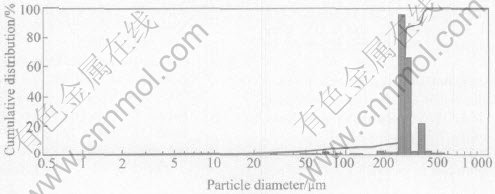
Fig.6 Droplet diameter distribution curve of Sn-4.0Ag-0.5Cu solder balls made by melt jet breakup process
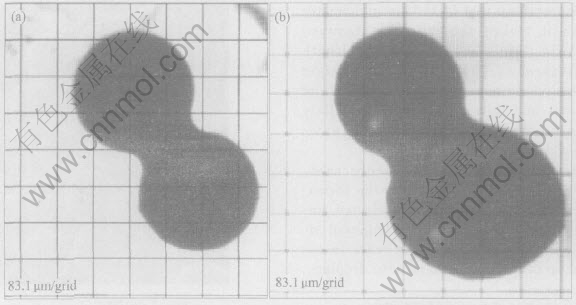
Fig.7 Coalesced particle morphologies exhibiting form of dumbbell formed by two particles similar in
size(a) and snowman formed by one big particle and a smaller one(b)
4 CONCLUSIONS
1) The formation of capillary wave of molten metal jet was observed and measured through rapidly solidification. It shows that molten metal jet can be broken-up into uniform droplets under the condition of good match of disturbance frequency with orifice diameter.
2) An empirical formula, which can be written as λ=Cvib(σ/ρ)1/3f-2/3, to predict the relationship between wavelength of capillary wave and frequency of imposed vibration was obtained, where the value of imposed vibration coefficient Cvib tends to increase with increase of disturbance frequency and orifice diameter, and particularly, the value of Cvib ranges from 3 to 7 for tin melt jet.
3) Sn-4.0Ag-0.5Cu lead free solder ball with narrow distribution and good sphericity was produced. The molten metal jet breakup process is promising for effectively manufacturing solder balls.
REFERENCES
[1]Lau J. Ball Grid Array Technology [M]. New York: McGraw-Hill, 1995.
[2]Yim P, Chun J H, Ando T, et al. Production and characterization of mono-sized Sn-38wt% Pb alloy balls [J]. International J of Powder Metall, 1996, 32(2): 155-164.
[3]Rocha J C. Control of the UDS process for the Production of Solder Balls for BGA electronics packaging [D]. Cambridge, MA, USA: Department of Mechanical Engineering, MIT, S.M. Thesis, 1997.
[4]Orme M, Smith R F. Enhanced aluminum properties by means of precise droplet deposition [J]. J of Manufacturing Sci Eng, 2000, 122: 484-493.
[5]Orme M, Courter J, Liu Q, et al. Charged molten metal droplet deposition as a direct write technology [A]. MRS 2000 Spring Meeting [C]. San Francisco, CA, USA: Materials Research Society, 2000.
[6]Orme M, Bright A. Recent advances in highly controlled molten metal droplet formation from capillary stream break-up with applications to advanced manufacturing [A]. 2000 TMS Annual Meeting [C]. Nashville, TN, USA: The Minerals, Metals & Materials, 2000.
[7]Lee Y T. The Influence of External Excited Waveform on Liquid Jet Breakup[D]. Taiwan: Cheng Kung University, 2001.
[8]Masayoshi D, Mitsuji S. Evaluation of lead-free solder balls produced by uniform droplet spray method [J]. Journal of Hitachi Metal Technology, 2002, 18: 43-50.
[9]Rayleigh J W S. On the instability of jets [A]. Proceedings of the Royal Society of London [C]. London: London Math Society, 1878. 4-13.
[10]Weber C. Zum zerfall eines flussigkeitsstrahles[ J]. Ztschr F Angew Math Und Mech, 1931, 11: 136-154.
[11]Bogy D B. Drop formation in a circular liquid jet [J]. Ann Rev Fluid Mech, 1979, 11: 207-228.
[12]McCarthy M. Review of stability of liquid jets and the influence of nozzle design [J].Chem Engineering, 1974, 7: 1-20.
[13]Orme M. On the genesis of droplet stream micro-speed dispersions [J]. Physics of Fluids A, 1991, 3(12): 2936-2947.
[14]Gallego-Juarez J A. High Powerful Ultrasound, Encyclopedia of Electrical and Electronics, Engineering [M]. New York: John Wiley & Sons Inc, 1999.
[15]Forrest B. Modeling Faraday Excitation of a Viscous Fluid [D]. USA: Department of Mathematics, Harvey Mudd College, 2002.
Foundation item: Project(2002AA322040) supported by the National High-Tech Research and Development Program of China
Received date: 2005-02-17; Accepted date: 2005-06-07
Correspondence: ZHANG Shu-guang, Professor, PhD; Tel: +86-21-62932569; Fax: +86-21-62933074; E-mail: zhangshug@sina.com


