J. Cent. South Univ. (2020) 27: 2424-2439
DOI: https://doi.org/10.1007/s11771-020-4459-y
A practical constitutive theory based on egg-shaped function in elasto-plastic modeling for soft clay
JIANG Jia-qi(蒋佳琪)1, 2, XU Ri-qing(徐日庆)1, 2, YU Jian-lin(俞建霖)1, 2,QIU Zhi-jian(裘志坚)3, QIN Jian-she(秦建设)3, ZHAN Xiao-bo(詹晓波)4
1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University,Hangzhou 310058, China;
2. Engineering Research Center of Urban Underground Space Development of Zhejiang Province,Hangzhou 310058, China;
3. Hangzhou Metro Group Co., Ltd., Hangzhou 310020, China;
4. Zhongtian Construction Group Limited Company, Hangzhou 310008, China
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract:
An exploratory discussion is presented on the application of egg-shaped function in elasto-plastic constitutive analysis for soft clay. Two main tasks of the paper are: 1) to propose a complete yield criterion based on egg-shaped function and supplement its definition in the deviatoric section, and then a yield criterion suitable for 3D stress conditions is obtained; 2) to elaborate its numerical implementation based on the drained triaxial tests. During the above discussion, a non-associated flow rule is proposed, in which the stress-dilatancy relationship in most classical theory is replaced by a linear dependence between the stress state parameter η and the rotation angle γ of the plastic potential surface. Thereafter, isotropic and kinematic hardening behavior is considered by employing the hardening parameter H, which can be expressed as the function of plastic work Wp. Finally, comparisons between numerical results and test data on Taizhou soft clay are made to verify the effectiveness of the proposed model.
Key words:
egg-shaped function; elastoplasticity; yield criterion; non-associated flow；
Cite this article as:
JIANG Jia-qi, XU Ri-qing, YU Jian-lin, QIU Zhi-jian, QIN Jian-she, ZHAN Xiao-bo. A practical constitutive theory based on egg-shaped function in elasto-plastic modeling for soft clay [J]. Journal of Central South University, 2020, 27(8): 2424-2439.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-020-4459-y1 Introduction
A variety of constitutive models with different levels of complexity have been proposed to simulate the elastoplastic behavior of cohesive and frictional materials. Among those models, the modified Cam clay (MCC) model [1] and the Mohr-Coulomb model are the most representative and popular in engineering analysis. Despite that, various extended formulations available for complex stress conditions can also be found in the geotechnical literature [2-10].
For establishing an efficient constitutive model, different mechanical behaviors should be taken into consideration, e.g., elastic properties, cohesion, pressure-sensitive yielding, viscoplasticity, plastic flow and anisotropy [11-13]. These properties are almost related to the performance of yield function and can be reproduced by various mathematical mechanisms. Latest researches corroborate that a micromechanical constitutive modeling appears to be more powerful because the microstructural effect (e.g., fabric, inter-aggregates contact, destructuring etc.) can be account for [14-16]. Both macro- and micro-scale tests show that the properties of undisturbed samples are significantly distinct from reconstituted one, such as stiffer stress-strain relationship, large-sized porous structure. From this perspective, many soil behaviors can be interpreted by a more reliable mechanism. For example, yielding is considered to be induced by the debonding or breakage of particles [17], and the local strains are highly non-uniform during the loading process [18, 19].
At early stage, most yield functions are linear and open in the meridian plane, such as the von Mises, the Mohr-Coulomb and the Druck-Prager criteria, and then gradually evolved into the non-linear and closed (cap model) type [20], e.g., MCC model. Similarly, the shape of yield curves in the deviatoric plane has evolved from circle to curved polygon (see Figure 1, classic yield criteria in the deviatoric plane are illustrated).
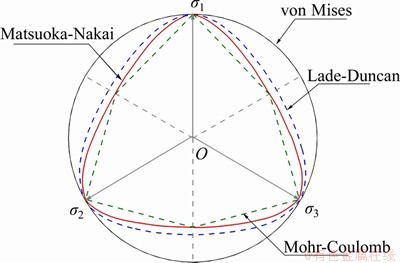
Figure 1 Yield locus of classic failure criteria in deviatoric plane
However, some classic yield criteria become inefficient when facing complex geotechnical problems. In such case, the spatially mobilized plane (SMP) criterion [21, 22] which is capable of considering the influence of intermediate principal stress, seems more useful. Since then, the 3D failure criterion has been widely recognized. For instance, MITSUTOSHI [23] developed a three-dimensional Coulomb strength model in which hypothesis of existence of the failure plane was emphasized. A 3D tij model based on the SMP criterion was proposed in elastoplastic modeling for normally and over-consolidated soils [24]. MORTARA [25-27] generalized the Lade-Duncan criterion and SMP criterion into a unified 3D elastoplastic constitutive framework. LU et al [28] developed a nonlinear unified strength model based on the characteristic stress concept. One remarkable feature for these yield criteria is: representations of meridian and deviatoric plane are coupled, which is adverse for geometric interpretation.
Generally speaking, the failure criterion for 3D stress state can be well established by various approaches through rigorous mathematical demonstration. At present, g(θ) method is widely applied for generalizing constitutive models [29-32]. Thus, three-dimensional yield surfaces are obtained by rotating yield curves from triaxial compression along the shape function g(θ) in the π-plane. More recently, another method called “Transformed Stress Method” has been proposed and successfully applied to generalize constitutive models [33-36]. As stated by YAO [33], discontinuous curvature may appear when the g(θ) method is employed for generalizing constitutive models, while such deficiency could be eliminated by a transformation mapping from the σi space to the transformed stress space as long as the deviator stress under the triaxial compression condition can be expressed explicitly by the stress invariants.
The egg-shaped function was firstly introduced into the elasto-plastic constitutive model by REN et al [37] and XU et al [38, 39], considering the following properties of egg-shaped function: 1) It’s a cap model in which properties such as bonding effect and pressure-sensitive yielding could be easily incorporated, and the corresponding yield curves in the meridional plane can be either “teardrop” type or “bullet” type, if appropriate parameters are selected. 2) It’s smooth, differentiable and retains full convexity in principal stress space. This eliminates the singularity and enables the use of an efficient implicit integration algorithm for the numerical procedure. However, REN and XU et al have not given further discussion about the deviatoric plane, and only several g(θ) expressions in literature are recommended. For example, Eq. (1) proposed by ZIENKIEWICZ and PANDE [40] is employed as the smooth approximation of the Mohr-Coulomb hexagonal deviatoric section. Certainly, such treatment is acceptable, while as for the completeness of this theory, it seems to be a little insufficient.
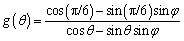(1)
where φ is the frictional angle.
In this paper, the egg-shaped function will be further developed to form a complete strength theory based on previous work, and its application in elastoplastic constitutive model will be discussed in detail. It will be helpful for readers to understand or apply this model in a more efficient way.
2 Yield and failure criterion
2.1 Egg-shaped function and its basic properties
The egg-shaped function was previously introduced by REN et al [37] and XU et al [38, 39] to characterize the yield and failure behavior of geomaterials, and can be rewritten in a generalized form:
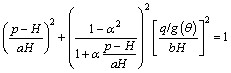(2)
Equation (2) is expressed in terms of mean stress p, deviatoric stress q and Lode angle θ, which are defined as:
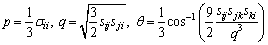(3)
where σij (i, j=1, 2, 3) is the Cauchy stress tensor and sij=σij-σkk·δij/3 presents the deviatoric stress tensor (where δij is the Kronecker delta). Note that, the stress discussed in this paper, for geomaterials, always refers to the effective stress.
Parameters a, b, α control the shape of the yield surface in the meridian plane. H is the hardening parameter, which can be represented as the function of plastic work Wp. Yield curve defined by Eq. (2) appears as a closed surface centered to the hydrostatic axis with curved generatrixes whose curvature is ruled by parameter α, which can be specified in the generalized range -1<α<1. In particular, for most geomaterials, a value less than
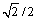is preferred, which is restricted by the requirement of convexity. Products aH and bH represent the radius of long and short axes, respectively. As it can be inferred from Eq. (2), the value of a, defined in the range a≥1, is able to characterize the bonding effect (or tensile strength) of cohesive soil (geomaterials) when a>1. Such bonding effect or tensile strength has been confirmed to be widely existing in natural materials. For example, an initial maximum strength line with bond cohesion σb>40 kPa was observed from the intact samples of Gulf Guinea [19]. Figure 2 shows the representative shape of yield surface governed by Eq. (2) for g(θ)=1.
As shown in Figure 2, yield surface governed by egg-shaped function can be either teardrop type or bullet type, and even elliptical type, depending on the value of α, positive or negative. On the other hand, as for cohesiveless soils, a=1 is needed; otherwise, the vertex of yield surface will not cross the coordinate origin.
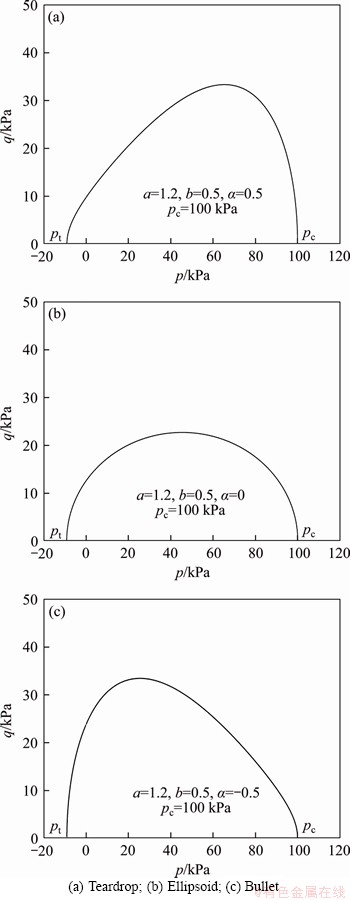
Figure 2 Representative shapes of egg-shaped yield function in meridian section:
The egg-shaped yield surface is compared with some other criteria [27, 41, 42] in the meridian plane for triaxial compression condition. As shown in Figure 3, in the normalized plane q/qmax, p/(pt+pc), a good agreement is obtained by appropriate parameter selection, only slight difference exists in the tensile-shear region for teardrop type. pc and pt are the yield strength under isotropic compression and tension, respectively. qmax represents the peak value of the yield curve. As indicated in Figure 2, pc and pt denote the intersection of the yield surface and the p-axis, respectively, Solving Eq. (2) by setting q=0 will yield
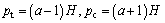(4)
g(θ) in Eq. (2) defines the shape of the yield surface in the deviatoric plane, and reflects the dependency of yield function on the Lode angle θ. Many shape functions for the π-plane have been proposed [43-48].
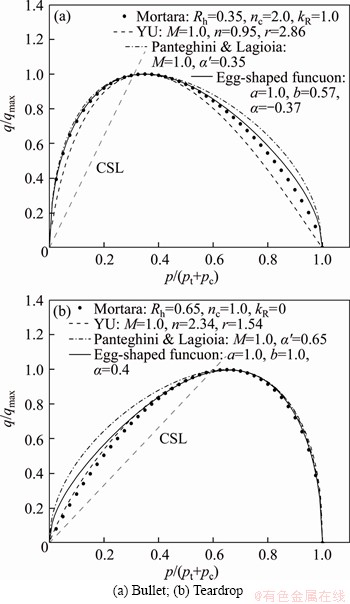
Figure 3 Comparison among some existing yield criteria in meridian plane:
2.2 Yield locus in deviatoric plane
In this section, an extended yield criterion based on the egg-shaped function (we may call it “dual egg-shaped yield criterion”) will be presented. To begin with, assuming that the meridional plane and deviatoric plane coincide at the origin, as depicted in Figure 4, and σ1-axis being the starting direction of θ. OQ represents the deviator stress in the π-plane.
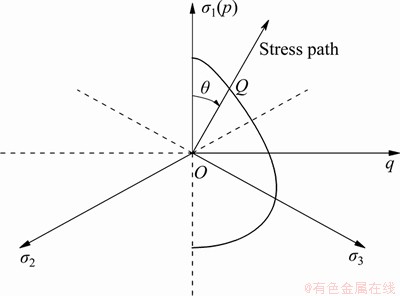
Figure 4 Schematic diagram of egg-shaped function in deviatoric plane
Then the egg-shaped function for deviatoric section can be rewritten as:
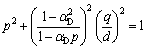(5)
where αD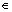
[0, 1] is a curvature parameter and subscript “D” refers to the deviatoric plane. Parameter d presents the radius of the short axis. Equation (5) can also be reformulated in polar coordinate as:
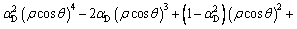
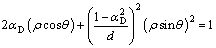(6)
The implicit function ρ(θ) determined by Eq. (6) is employed as the shape function g(θ) in the deviatoric plane. However, ρ(θ) is only defined in the range 0≤θ≤θ*. θ*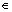[0, π/2] is a stagnation at which a minimum value ρ(θ*) is reached.Equation (6) is then differentiated and solved to obtain θ* and ρ(θ*):
(7a)
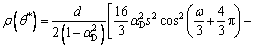
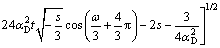(7b)
where
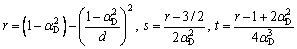(7c)
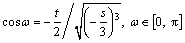(7d)
According to the property of g(θ), only values defined in the range [0, π/3] should be determined while the rest can be obtained from trigonometrical and periodic considerations. To match this property, a linear mapping is introduced here:
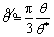(8)
Following the method of BARDET [29], a material parameter β is introduced which represents the strength ratio of triaxial extension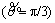 
to triaxial compression
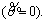Based on the previous derivation, it’s easy to identify that ρ(θ*)=β, so parameter d could be determined from β. According to the definition by BARDET, β varying from 0.5 to 1, can be related to the friction angle φ via
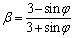(9)
Equation (9) implies that β decreases from 1 to 0.5 as φ increases from 0° to 90°. For most geotechnical materials, the friction angle is generally less than 45°, and the corresponding β is greater than 0.62. Figure 5 shows different shapes of g(θ) with different parameter β.
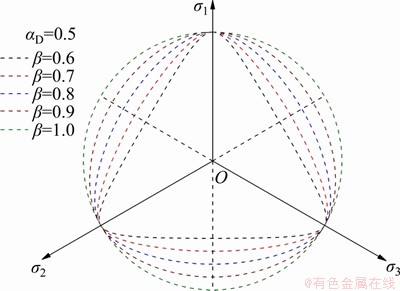
Figure 5 Effect of parameter β on yield curves in deviatoric plane
It can be concluded that g(θ) is continuous and differentiable for all values of θ, and decreases monotonically in the range 0≤θ≤π/3. Intuitively, the smaller the β is, the more the yield curves tend to be a triangle; In contrast, it is close to a circle when β approaches to 1. What’s more, the convexity can be guaranteed by a valid β.
The proposed egg-shaped g(θ) function is compared with some other Lode dependences for the same selected β (see Figure 6). Formulations used for comparison are reported in Table 1. Note that some formulations are given in a slightly different form with respect to their original formulation, so as to be consistent with the definition of the Lode angle given in this paper.
It can be observed from Figure 6 that, for a same β, the egg-shaped Lode dependence shows a very good agreement with the existing models when favorable parameters are selected. In addition, it can be clearly seen that as the curvature parameter αD increases from 0 to 1, the yield surface changes from circular to triangular shapes in the deviatoric plane.
By now, the proposed dual egg-shaped yield criterion is fully elaborated, with 5 model parameters a, b, α, αD and β needed to be determined. Figure 7 gives the dual egg-shaped yield surface in the principal stress space. Moreover, the hardening parameter H, which is related to the isotropic compression yield strength pc, also needs to be specified through suitable hardening laws.
3 Plastic potential and flow rule
The direction of plastic strain increment vector is determined by the plastic potential within the framework of elastoplastic constitutive theory. In form, plastic potential function can be either same or different from the yield function, i.e. associated and non-associated flow rule. For various yield function, including egg-shaped yield criterion discussed in this study, a non-associated flow rule is generally more representative of soil behavior than an associated one. In this section, a plastic potential theory based on the egg-shaped function is described to improve the performance of this constitutive model.
3.1 Strain decomposition
The total strain increment dεij is divided into elastic and plastic parts:
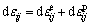(10)
Elastic strain increments part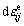
can be calculated using the generalized Hook’s law:
(11)
where K and G are the elastic bulk modulus and elastic shear modulus, respectively. Elastic bulk modulus K is generally determined by the rebound segment of isotropic compression test, which can be expressed as [49]:
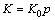(12)
Elastic shear modulus G can be determined by the unloading and reloading section of conventional triaxial test and can be approximately written as [50]:
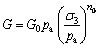(13)
where pa is the standard atmospheric pressure of about 101 kPa. In total, three elastic constants K0, G0 and n0 should be assigned.
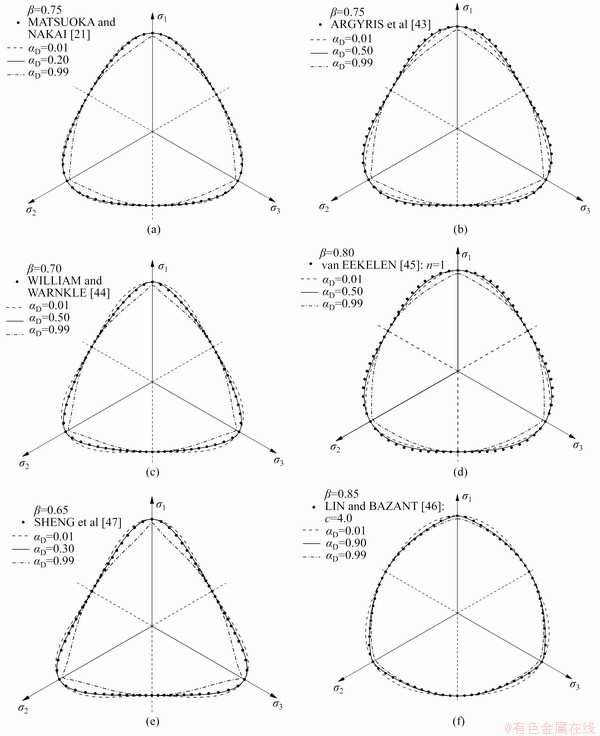
Figure 6 Comparison among some existing Lode dependences and function g(θ)
Table 1 Different Lode dependences in literature
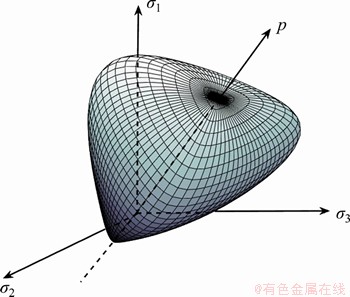
Figure 7 Dual egg-shaped yield surface in principle stress space
Plastic strain increments are determined by the plastic potential surface function Ω in the stress space. For a specific stress state, the direction of its plastic strain increment is perpendicular to the plastic potential surface, that is the so-called orthogonal flow rule, i.e.,
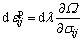(14)
where dλ is the plastic multiplier.
The concept of plastic potential surface function was applied to the analysis of soil deformation by ROSCOE and POOROOSHASB [51], based on experimental observation. POOROOSHASB et al [52] further pointed out that the plastic flow direction during loading is only related to the stress state, regardless of the stress path to this state. This argument was later verified by LADE and DUNCAN [53]. Nowadays, many constitutive models follow this principle [54]. More precisely, the following assumption is widely acknowledged by most constitutive theories (e.g. the Cam-Clay model):
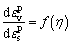(15)
Equation (15) implies that the plastic strain increment ratio is uniquely determined by the stress ratio η (η=q/p).
3.2 Egg-shaped plastic potential surface
To begin with, the corresponding parametric expression of the egg-shaped function can be expressed as:
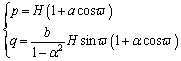(16)
Similarly, a plastic potential function Ω with the same form as egg-shaped function can be written as:
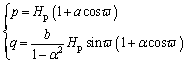(17)
Equations (16) and (17) which represent the yield surface and the plastic potential surface respectively employ the same model parameters a, b, α that can be obtained from the triaxial compression tests. The only difference is that the center of the plastic potential surface does not necessarily coincide with the center of yield surface, so an alternative parameter Hp of the plastic potential function is used to distinguish from the hardening center H of the yield surface. Moreover, extra rotation is required for Eq. (17) to improve the reliability of the plastic potential surface. As shown in Figure 8, a clockwise rotation of angle γ for the plastic potential surface can be achieved by:
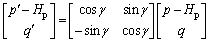(18)
where p′ and q′ refer to the mean stress and deviatoric stress after rotation.
For arbitrary stress state D on the stress path, Eqs. (16) and (18) both should be satisfied.
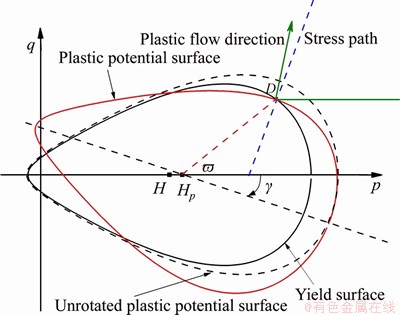
Figure 8 Inclined egg-shaped plastic potential surface
Furthermore, the plastic strain increment ratio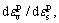 
i.e., the exterior normal direction of the plastic potential surface, can be determined by the experimental results.
Substituting Eq. (17) into Eq. (18) and differentiating, we can obtain:
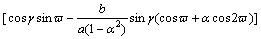(19)
Equations (18) and (19) can be solved jointly based on the known stress and the corresponding plastic strain increment ratio, which are obtained from the drained triaxial tests. Although it seems a little complicated, there is no difficulty in numerical solutions, e.g., MATLAB code. Then the unknow 
, Hp and γ are determined.
3.3 Experimental observation
In order to further investigate the evolution law of the inclined plastic potential surface above mentioned, five groups of drained triaxial tests were carried out, whose confining pressure were 25, 50, 100, 200 and 400 kPa, respectively. Test samples were taken from a construction site in Taizhou, China. The basic physical properties are given in Table 2.
Table 2 Physical and mechanical properties of soil sample
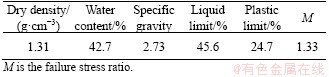
Remolded samples were used for triaxial tests. When preparing specimens, the dried soil samples were crushed into fine powder that could pass through a 0.5-mm sieve, then the screened samples were sealed and preserved. All the tests were done on 39.1-mm-diameter and 80-mm-high specimens that were carefully compacted in 4 layers. The initial void ratio e0 of all specimens was controlled at about 1.14. The drained triaxial tests were carried out with the GDS triaxial system (GDSTTS) at Zhejiang University.
At the beginning of the test, all the specimens were saturated under a back pressure of 300 kPa. After that, a B-check process was performed to confirm that its B value was at least 0.98 and then subsequent isotropic consolidation could be implemented. The loading process was controlled by deviatoric stress q and the corresponding loading rate was 0.08 kPa/min. This loading rate was selected to ensure that the excess pore pressure will not accumulate.
Table 3 shows the correspondence between the plastic strain increment ratio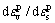 
of the test results and the rotation angle γ of the plastic potential surface. It can be concluded that the initial and final values of γ, denoted as γ0 and γd, changed a little under different confining pressure, and stabilized at around 80° and -55°, respectively. This observation implies that γ0 and γd are constants independent of the stress path.
Another notable feature is the transition of rotation angle γ from positive to negative. When γ<0, it corresponds to the counterclockwise tilt of the plastic potential surface (see Figure 10). One possible interpretation for this observation is: if we assume that γ≥0 always holds and γ=0 as it reaches the failure line. Under such condition, the plastic potential surface completely coincides with the yield surface when the failure state is reached. As we know, a significant characteristic of failure state is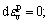 
in that case, the critical state line must pass through the peak of the plastic potential surface, as well as the yield surface. However, some research results [41, 55, 56] imply that the critical state line does not necessarily pass through the peak of the yield surface, no matter how the type of yield surface is. For example, according to the test results of this study, the critical state line generally intersects the egg-shaped yield surface on the left side of the center. So, when the soil fails, only counterclockwise rotation of the plastic potential surface that 
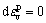can be guaranteed. At the same time, it can be found that the relative position of the intersection of the critical state line and the yield surface is also stable, which determines that the value of γd is less affected by the stress path.
3.4 Normalized rotation angle
A crucial argument in the critical state soil mechanics is that soil behavior is mainly determined by its current physical state (including stress, strain and void ratio etc.) and independent of the stress path [57]. YU [41] once introduced a state parameter which described the distance between current state and critical state to develop his constitutive model. Inspired by this method, a similar operation is taken into consideration whether the variation of the rotation angle γ can be characterized by the corresponding state parameters of the soil.
From the previous analysis we know, rotation angle γ varies in the range γ0-γd , and considering the stability of γ0 and γd , a normalized rotation angle variable γ′ is proposed:
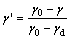(20)
Obviously, the normalized rotation angle γ′ranges from 0 to 1. Meanwhile, the stress ratio η is employed again as a state parameter based on Eq. (15). Since γ′ is a normalized parameter representing the change of angle, here we suggest another normalized parameter ξ to characterize the stress state:
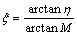(21)
The normalized parameter ξ also ranges from 0 to 1, whose geometric interpretation is defined as the angle ratio of stress vector direction (p, q) to the critical state line direction in the meridional plane. Intuitively, parameter ξ can also describe the difference between the current state and the critical state, not by the distance, but by the angle.
Table 3 Calculated value of rotation angle γ
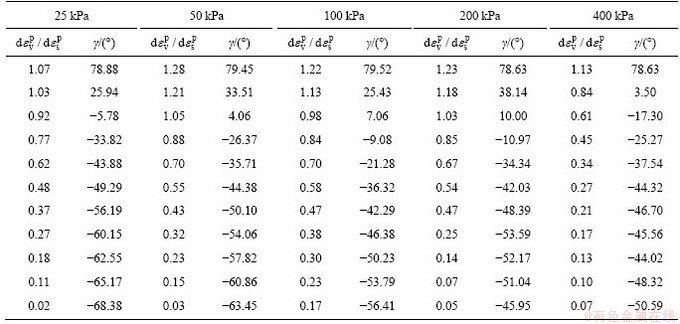
Figure 9 displays the relationship between parameters ξ and γ′, which are collected from the above drained triaxial tests. An approximate piecewise linear dependence exists between them. After further analysis, the segment point is located round the turning point where rotation angle γ changes from positive to negative. This transformation is caused by the irregular curvature distribution of the egg-shaped plastic potential surface during rotation. Thus, this relationship could be summarized as:
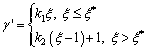(22)
where k1 and k2 are material constants to be determined, and two theoretical values of the endpoints (0, 0) and (1, 1) are taken into consideration. Then the segment point ξ* can be obtained by:
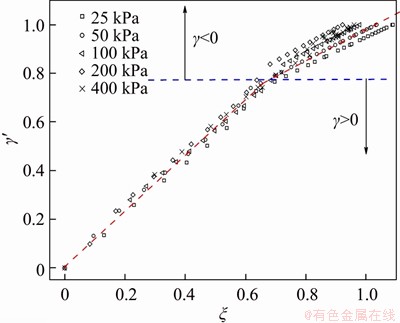
Figure 9 Relationship between normalized rotation angle γ′ and stress state parameter ξ
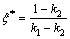(23)
3.5 Non-associated flow rule
As mentioned above, γ0 and γd, representing the initial and final values of the rotation angle respectively, can be solved jointly from Eqs. (18) and (19). In numerical implementation, these two constants can be estimated using the value of M if we set:
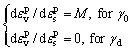(24)
The complete plastic flow rule applicable for the egg-shaped yield criterion can be obtained based on the discussion above. As shown in Figure 10, black and red solid lines indicate the yield surface and plastic potential surface of current state, respectively. For arbitrary stress state D on the stress path, its plastic flow direction could be calculated with the help of Eq. (22), which is utilized firstly to determine the rotation angle of the plastic potential surface, then it is easy to determine the plastic flow direction according to the orthogonal flow rule.
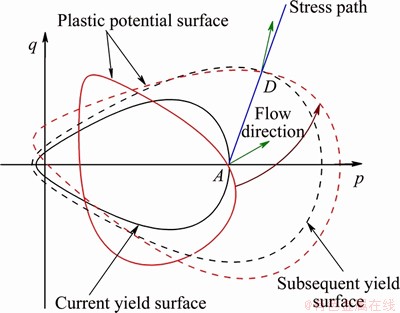
Figure 10 Schematic diagram of plastic flow rule
Such plastic flow rule, employing a plastic potential function with the same form as the yield function, is essentially a non-associated flow rule. Besides the basic parameters of yield function a, b and α, this model only requires 2 parameters, k1 and k2, describing the variation of the rotation angle of the plastic potential surface.
4 Hardening law for variable H
To account for isotropic hardening as well as kinematic hardening when loading, a mix hardening mode is introduced in which the hardening parameter H, for the egg-shaped yield function, is generally written as the function of plastic work Wp:
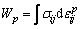(25)
Figure 11 shows the correlation between the data for plastic work obtained from triaxial tests and the calculated hardening parameter H. The plastic work occurring in consolidation is not included here. For stress at low levels, the hardening parameter H increases slowly with the increasing plastic work, and then increases rapidly, after that it slows down until reaching the failure state. The initial hardening parameter H0 which represents the hardening parameter corresponding to plastic work during consolidation can be directly determined by:
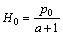(26)
where p0 is the preconsolidation pressure.
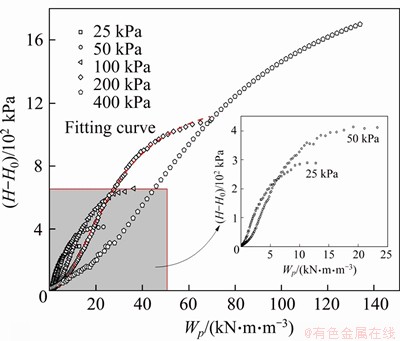
Figure 11 Relation between hardening parameter H and plastic work Wp
The correlation reflected by Figure 11 can be approximated as:
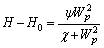(27)
where ψ and χ are model parameters whose value for this test can be found in Table 4. Based on a nonlinear regression analysis, these parameters could be further summarized by the following empirical formula:
(28)
where m1, m2, m3, m4 are material constants that could be determined directly by the conventional triaxial tests. For Taizhou soft clay in our tests, fitting results of m1, m2, m3, m4 are 7.76, 0.754, 129.6, 2.61, respectively, and correlation coefficient R2 are 0.998 and 0.997 (see Figure 12).
Table 4 Regression results for hardening law Eq. (27)
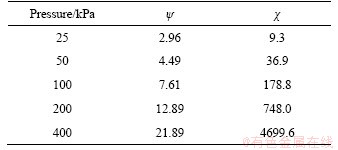
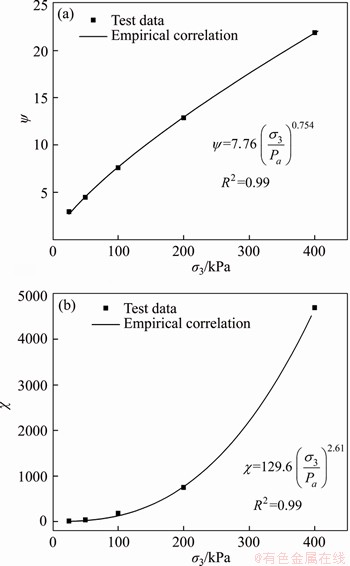
Figure 12 Regression analysis of parameter ψ and χ
5 Numerical verification
After the above discussion, an elastoplastic constitutive model based on the egg-shaped function has been completely presented, a total of 12 model parameters are required, including three elastic constants K0, G0, n0, three yield criterion parameters a, b, α, two parameters for non- associated flow rule k1, k2 and four hardening parameters m1, m2, m3, m4. For three-dimensional stress condition, additional yield parameters αD and β are also necessary. Model parameters used in numerical analysis of Taizhou soft clay can be found in Table 5.
Table 5 Material constants used for numerical analysis
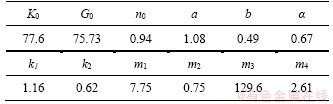
Figure 13 shows the comparison between the numerical results of egg-shaped constitutive model and the measured results of the conventional triaxial tests and a total agreement can be obtained.
As displayed in Figure 13, the predicted results are relatively accurate at high stress levels. One possible explanation for such phenomenon is that the plastic flow rule presented in this paper is more sensitive to the rotation angle γ at low stress state, which will lead to slight deviation. Another potential reason is inaccurate estimation of model parameters, but these are controllable overall.
To estimate the selection of model parameters in this paper, an optimization procedure for identifying parameters was performed, following the methodology proposed by JIN et al [58, 59]. A fitness function with two criteria was considered:
(29)
The result shows that simulation error (the difference between the experiments and simulations) for model parameters in Table 5 is about 10.9%; while for optimised parameters K0=72.63, G0=85.27, n0=0.925, a=1.12, b=0.52, α=0.67, k1=1.18, k2=0.613, m1=6.44, m2=0.73, m3=104.7, m4=2.23, its value is 9.47%, which confirms that parameter selection in this paper is reliable.
6 Conclusions
This paper has outlined a constitutive model for defining the elastoplastic behavior of geomaterials based on the egg-shaped function. At the beginning, one prominent advantage of the previously proposed egg-shaped function, which was able to describe the yield curves in the meridian section ranging continuously from “teardrop” to “bullet” type, has been further enhanced by extending this function to the deviatoric plane, resulting in a complete egg-shaped yield criterion for 3D stress state. This expansion has been achieved by introducing two additional parameters: 1) αD, which controls the curvature of yield curves in the deviatoric plane; and 2) β, material parameter to quantify the ratio of tensile and compressive capacity. Numerical comparison with other existing models in the deviatoric representation also has revealed a good capability of this new expression.
Furthermore, the plastic potential can be assumed to be in the same form as yield surface,i.e., egg-shaped function. However, according to tests observation, the egg-shaped plastic potential surface will rotate as the plastic deformation develops. Interestingly, it can be found that the rotation angle γ of the plastic potential surface linearly depends on the stress ratio η by further analysis. Thanks to such dependence, it’s possible to establish a new flow rule applicable to the egg-shaped function. Distinguished from some classic models, the dilatancy relationship in this model has been constructed based on the stress state and rotation angle. Thus, this plastic flow law is a non-associated one in nature and can reflect the characteristics of plastic deformation.
Isotropic and kinematic hardening has been incorporated to this model. Hardening parameter H in Eq. (2) is expressed in form of plastic work Wp, an appropriate correlation Eq. (27) has been established from regression analysis. Then the elasto-plastic constitutive model based on egg-shaped function is completed. To demonstrate the model validation, comparisons of model predictions with drainage triaxial test data were performed, which showed an overall good agreement. Finally, the optimization for parameters further confirmed that parameters selection in this paper is reliable.
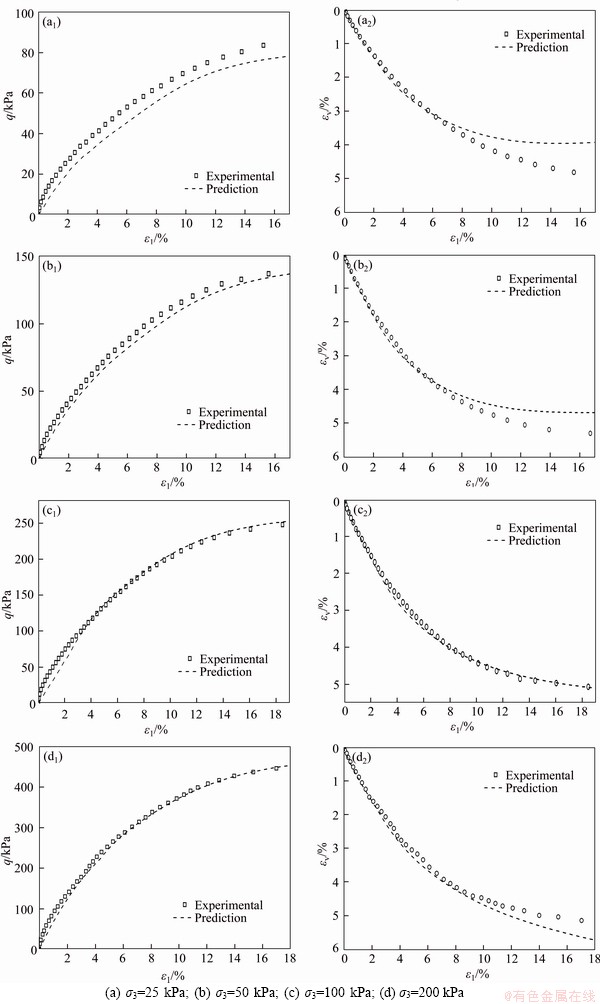
Figure 13 Comparisons between numerical and experimental results:
References
[1] ROSCOE K H, BURLAND J B. On the generalised stress-strain behaviour of ‘wet’ clay [C]// HEYMAN J, LECKIE F A. Engineering Plasticity. Cambridge University Press, 1968: 535-609. DOI: https://doi.org/10.1016/0022- 4898(70)90160-6.
[2] MCDOWELL G R, HAU K W. A generalised modified Cam clay model for clay and sand incorporating kinematic hardening and bounding surface plasticity [J]. Granular Matter, 2004, 6(1): 11-16. DOI: https://doi.org/10.1007/ s10035-003-0152-8.
[3] DAFALIAS Y F, MANZARI M T, PAPADIMITRIOU A G. SANICLAY: Simple anisotropic clay plasticity model [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(12): 1231-1257. DOI: https:// doi.org/10.1002/nag.524.
[4] YAO Yang-ping, HOU Wei, ZHOU An-nan. UH model: Three-dimensional unified hardening model for overconsolidated clays [J]. Géotechnique, 2009, 59(5): 452-469. DOI: https://doi.org/10.1680/geot.2007.00029.
[5] YAN W M, LI X S. A model for natural soil with bonds [J]. Géotechnique, 2011, 61(2): 95-106. DOI: https://doi.org/ 10.1680/geot.8.p.061.
[6] YIN Zhen-yu, XU Qiang, HICHER P Y. A simple critical- state-based double-yield-surface model for clay behavior under complex loading [J]. Acta Geotechnica, 2013, 8(5): 509-523. DOI: https://doi.org/10.1007/s11440-013-0206-y.
[7] ZHONG Zhi-hui, YANG Guang-hua, FU Xu-dong, WEN Yong, ZHANG Yu-cheng. Numerical verification of similar Cam-clay model based on generalized potential theory [J]. Journal of Central South University, 2014, 21(12): 4707-4713. DOI: https://doi.org/10.1007/s11771-014- 2480-8.
[8] JOCKOVIC S, VUKICEVIC M. Bounding surface model for overconsolidated clays with new state parameter formulation of hardening rule [J]. Computers and Geotechnics, 2017, 83: 16-29. DOI: https://doi.org/10.1016/j.compgeo.2016.10. 013.
[9] HAN J, LIANG H, CAO C, BI Z, ZHU Z. A mechanical model for sheared joints based on Mohr-Coulomb material properties [J]. Géotechnique Letters, 2018, 8(2): 92-96. DOI: https://doi.org/10.1680/jgele.17.00106.
[10] YAO Yang-ping, LIU Lin, LUO Ting, TIAN Yu, ZHANG Jian-min. Unified hardening (UH) model for clays and sands [J]. Computers and Geotechnics, 2019, 110: 326-343. DOI: https://doi.org/10.1016/j.compgeo.2019.02.024.
[11] YIN Zhen-yu, CHANG C S, KARSTUNEN M, HICHER P Y. An anisotropic elastic-viscoplastic model for soft clays [J] International Journal of Solids and Structures, 2010, 47(5): 665-677. DOI: https://doi.org/10.1016/j.ijsolstr.2009.11.004.
[12] HAMMI Y, STONE T W, PALIWAL B, HORSTEMEYER M F, ALLISON P G. Smooth yield surface constitutive modeling for granular materials [J]. ASME Journal of Engineering Materials and Technology, 2017, 139(1): 011010. DOI: https://doi.org/10.1115/1.4034987.
[13] UEDA K, LAI S. Constitutive modeling of inherent anisotropy in a strain space multiple mechanism model for granular materials [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(3): 708-737. DOI: https://doi.org/10.1002/nag.2883.
[14] JIANG Ming-jing. New paradigm for modern soil mechanics: Geomechanics from micro to macro [J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 195-254. DOI: 10.11779/CJGE201902001. (in Chinese)
[15] ZENG Tao, SHAO Jian-fu, YAO Yao. A micromechanical- based elasto-viscoplastic model for the Callovo-Oxfordian argillite: Algorithms, validations, and applications [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2020, 44(2): 183-207. DOI: https:// doi.org/10.1002/nag.3006.
[16] PETALAS A L, DAFALIAS Y F, PAPADIMITRIOU A G. SANISAND-F: Sand constitutive model with evolving fabric anisotropy [J]. International Journal of Solids and Structures, 2020, 188-189: 12-31. DOI: https://doi.org/10.1016/ j.ijsolstr.2019.09.005.
[17] JIANG Ming-jing, YU Hai-sui, LEROUEIL S. A simple and effcient approach to capturing bonding effect in naturally microstrucutred sands by discrete element method [J]. International Journal for Numerical Methods in Engineering, 2007, 69(6): 1158-1193. DOI: https://doi.org/10.1002/ nme.1804.
[18] YIN Zhen-yu, CHANG C S. Microstructural modelling of stress-dependent behaviour of clay [J]. International Journal of Solids and Structures, 2009, 46(6): 1373-1388. DOI: https://doi.org/10.1016/j.ijsolstr.2008.11.006.
[19] YIN Zhen-yu, HATTAB M, HICHER P Y. Multiscale modeling of a sensitive marine clay [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(15): 1682-1702. DOI: https://doi.org/10.1002/ nag.977.
[20] YAO Yang-ping, LU De-chun, ZHOU An-nan, ZOU Bo. Generalized non-linear strength theory and transformed stress space [J]. Science in China, Series E: Technological Sciences, 2004, 47(6): 691-709. DOI: https://doi.org/ 10.1360/04ye0199.
[21] MATSUOKA H, NAKAI T. Stress-deformation and strength characteristics of soil under three different principal stresses [J]. Proceedings of the Japan Society of Civil Engineers, 1974, 232: 59-70. DOI: https://doi.org/10.2208/ jscej1969.1974.232_59.
[22] NAKAI T, MATSUOKA H. A generalised elastoplastic constitutive model for clay in three dimensional stresses [J]. Soils and Foundations, 1986, 26(4): 81-98. DOI: https://doi. org/10.3208/sandf1972.26.3_81.
[23] MITSUTOSHI Y. 3-D Coulomb’s failure criterion for various geomaterials [C]// LADE P V, NAKAI T. Geomechanics II: Testing, Modeling, and Simulation, ASCE. Resyon, VA, 2005: 71-86. DOI: https://doi.org/10.1061/ 40870(216)6.
[24] NAKAI T, HINOKIO M. A simple elastoplastic model for normally and over consolidated soils with unified material parameters [J]. Soils and Foundations, 2004, 44(2): 53-70. DOI: https://doi.org/10.3208/sandf.44.2_53.
[25] MORTARA G. A new yield and failure criterion for geomaterials [J]. Géotechnique, 2008, 58(2): 125-132. DOI: https://doi.org/10.1680/geot.2008.58.2.125.
[26] MORTARA G. A hierarchical single yield surface for frictional materials [J]. Computers and Geotechnics, 2009, 36(6): 960-967. DOI: https://doi.org/10.1016/j.compgeo. 2009.03.007.
[27] MORTARA G. A constitutive framework for the elastoplastic modelling of geomaterials [J]. International Journal of Solids and Structures, 2015, 63: 139-152. DOI: https://doi.org/ 10.1016/j.ijsolstr.2015.02.047.
[28] LU De-chun, MA Chao, DU Xiu-li, JIN Liu, GONG Qiu-ming. Development of a new nonlinear unified strength theory for geomaterials based on thr characteristic stress concept [J]. International Journal of Geomechanics, ASCE, 2017, 17(2): 4016058. DOI: https://doi.org/10.1061/ (asce)gm.1943-5622.0000729.
[29] BARDET J P. Lode dependences for isotropic pressure- sensitive elastoplastic materials [J]. ASME Journal of Applied Mechanics, 1990, 57(3): 498-506. DOI: https:// doi.org/10.1115/1.2897051.
[30] SHAO J F, ZHU Q Z, SU K. Modeling of creep in rock materials in terms of material degradation [J]. Computers and Geotechnics, 2003, 30(7): 549-555. DOI: https://doi. org/10.1016/s0266-352x(03)00063-6.
[31] LAGIOIA R, PANTEGHINI A. On the existence of a unique class of yield and failure criteria comprising Tresca, Von- Mises, Drucker-Prager, Mohr-Coulomb, Galileo-Rankine, Matsuoka-Nakai and Lade-Duncan [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 2016, 472(2185): 20150713. DOI: https://doi.org/ 10.1098/rspa.2015.0713.
[32] JIANG Hua. Three-dimensional failure criteria for rocks based on the Hoek–Brown criterion and a general Lode dependence [J]. International Journal of Geomechanics, 2017, 17(8): 04017023. DOI: https://doi.org/10.1061/(asce)gm. 1943-5622.0000900.
[33] YAO Yang-ping, WANG Nai-dong. Transformed stress method for generalizing soil constitutive models [J]. ASCE Journal of Engineering Mechanics, 2014, 140(3): 614-629. DOI : https://doi.org/10.1061/(asce)em.1943-7889.0000685.
[34] LU De-chun, LI Xiao-qiang, DU Xiu-li, LIANG Jing-yu. A simple 3D elastoplastic constitutive model for soils based on the characteristic stress [J]. Computers and Geotechnics, 2019, 109: 229-247. DOI: https://doi.org/10.1016/j.compgeo. 2019.02.001.
[35] CHEN Hao-hua, LI Lin, LI Jiang-pei, WANG Hui. Stress transform method to undrained and drained expansion of a cylindrical cavity in anisotropic modified cam-clay soils [J]. Computers and Geotechnics, 2019, 106: 128-142. DOI: https://doi.org/10.1016/j.compgeo.2018.10.016.
[36] WAN Zheng, SONG Chen-chen, MENG Da. A nonlinear strength criterion and transformation stress method [J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(4): 1210-1222. DOI: 10.6052/0459-1879-19- 039. (in Chinese)
[37] REN Fang, SHENG Qian, CHANG Yan-ting. Egg-shaped yield function for geotechnical engineering materials [J]. Chinese Journal of Geotechnical Engineering, 1993, 13(4): 33-39. DOI: 10.3321/j.issn:1000-4548.1993.04.005. (in Chinese)
[38] XU Ri-qing, YANG Lin-de, GONG Xiao-nan. Stress-strain constitutive relationship of boundary surface of soils [J]. Jounal of Tongji University (Nature & Science), 1997, 25(1): 29-33. (in Chinese)
[39] XU Ri-qing, WANG Xing-chen, RONG Xue-ning. Marco- and meso-scale parametric analysis of egg-shaped yield surface of structural soil [J]. International Journal of Offshore and Polar Engineering, 2014, 24(4): 301-308.
[40] ZIENKIEWICZ O C, PANDE G N. Some useful forms of isotropic yield surfaces for soil and rock mechanics [C]// GUDEHUS G. Finite Element in Geomechanics. London: John Wiley & Sons Ltd, 1977: 179-190.
[41] YU H S. CASM: A unified state parameter model for clay and sand [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1998, 22(8): 621-653. DOI: https://doi.org/10.1002/(sici)1096-9853(199808)22:8< 621::aid-nag937>3.0.co;2-8.
[42] PANTEGHINI A, LAGIOIA R. An extended modified Cam-Clay yield surface for arbitrary meridional and deviatoric shapes retaining full convexity and double homothety [J]. Géotechnique, 2018, 68(7): 590-601. DOI: https://doi.org/10.1680/jgeot.17.p.016.
[43] ARGYRIS J H, FAUST G, SZIMMAT J, WARNKE E P, WILLAM K J. Recent developments in the finite element analysis of prestressed concrete reactor vessels [J]. Nuclear Engineering and Design, 1974, 28(1): 42-75. DOI: https://doi.org/10.1016/0029-5493(74)90088-0.
[44] WILLAM K, WARNKE E P. Constitutive model for the triaxial behavior of concrete [C]// Seminar on Concrete Structure Subjected to Triaxial Stresses, ISMES. Bergamo, Italy, 1975: 17-19. DOI: https://dx.doi.org/10.5169/seals- 17526.
[45] van EEKELEN H A M. Isotropic yield surface in three dimensions for use in soil mechanics [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1980, 4(1): 89-101. DOI: https://doi.org/ 10.1002/nag.1610040107.
[46] LIN Feng-bao, BAZANT Z P. Convexity of smooth yield surface of frictional material [J]. ASCE Journal of Engineering Mechanics, 1986, 112(11): 1259-1262. DOI: https://doi.org/10.1061/(asce)0733-9399(1986)112:11(1259).
[47] SHENG D, SLOAN S W, YU H S. Aspects of finite element implementation of critical state models [J]. Computational Mechanics, 2000, 26(2): 185-196. DOI: https://doi.org/ 10.1007/s004660000166.
[48] HASHIGUCHI K. A proposal of the simplest convex-conical surface for soils [J]. Soils and Foundations, 2002, 42(3): 107-113. DOI: https://doi.org/10.3208/sandf.42.3_107.
[49] GUO Rui-ping, LI Guang-xin. Elasto-plastic model of soil with a function of plastic work as the hardening function [J]. Journal of Tsinghua University (Science and Technology), 2000, 40(5): 125-127. DOI: 10.16511/j.cnki.qhdxxb.2000. 05.034. (in Chinese)
[50] LIU Xin-rong, ZHONG Zu-liang, ZHANG Yong-xing, WANG Ji-ming. Elastoplastic modeling of unsaturated intact Q2 loess with plastic work as hardening parameter [J]. Rock and Soil Mechanics, 2009, 30(5): 1215-1220. DOI: 10.16285/j.rsm.2009.05.028. (in Chinese)
[51] ROSCOE K H, POOROOSHASB H B. A theoretical and experimental study of strains in triaxial tests on normally consolidated clays [J]. Géotechnique, 1963, 13(1): 12-38. DOI: https://doi.org/10.1016/0022-4898(64)90162-4.
[52] POOROOSHASB H B, HOLUBEC I, SHERBOURNE A N. Yielding and flow of sand in triaxial compression: Part I [J]. Canadian Geotechnical Journal, 1966, 3(4): 179-190. DOI: https://doi.org/10.1139/t66-023.
[53] LADE P V, DUNCAN J M. Stress-path dependent behavior of cohesionless soil [J]. ASCE Journal of Geotechnical Engineering, 1976, 102(1): 51-68.
[54] ZHOU Cheng, LEROUEIL S, FAFARD M, GHORBEL S. Constitutive modeling of kinematic hardening behavior of saturated anisotropic soils [J]. ASCE International Journal of Geomechanics, 2017, 17(3): 04016063. DOI: https:// doi.org/10.1061/(asce)gm.1943-5622.0000732.
[55] HUANG Wen-xi. Theory of elastoplastic stress-strain model for soil [J]. Rock and Soil Mechanics, 1979, 1(1): 1-20. DOI: 10.16285/j.rsm.1979.01.002. (in Chinese)
[56] SULTAN N, CUI Y J, DELAGE P. Yielding and plastic behavior of Boom clay [J]. Géotechnique, 2010, 60 (9): 657- 666. DOI: https://doi.org/10.1680/geot.7.00142.
[57] SCHOFIELD A N, WORTH C P. Critical state soil mechanics [M]. New York: McGraw-Hill, 1968.
[58] JIN Yin-fu, YIN Zhen-yu, SHEN Shui-long, HICHER P Y. Investigation into MOGA for identifying parameters of a critical-state-based sand model and parameters correlation by factor analysis [J]. Acta Geotechnica, 2016, 11(5): 1311- 1145. DOI: https://doi.org/10.1007/s11440-015-0425-5.
[59] JIN Yin-fu, WU Ze-xiang, YIN Zhen-yu, SHEN Shui-long. Estimation of critical state-related formula in advanced constitutive modeling of granular material [J]. Acta Geotechnica, 2017, 12(6): 1329-1351. DOI: https://doi.org/ 10.1007/s11440-017-0586-5.
(Edited by YANG Hua)
中文导读
一种基于蛋形函数的实用软土弹塑性本构理论
摘要：本文针对蛋形函数在软黏土弹塑性本构分析中的应用进行了讨论。两项主要的研究任务分别为：1) 以蛋形函数为基础，提出完整的蛋形屈服理论，补充其在偏平面中的定义，得出三维应力条件下的强度屈服准则；2) 具体阐述蛋形本构模型的数值实现方法。首先，根据排水三轴试验结果，提出一种非关联塑性流动法则，其中大多数经典本构理论中的应力-剪胀关系被归一化应力状态参数η与塑性势面旋转角γ之间的线性关系所代替。进一步，通过采用硬化参数H (H可以表示为塑性功Wp的函数)来表征土体等向以及运动硬化行为。最后，将蛋形模型的数值计算结果与台州软土试验数据进行对比，验证了本文模型的有效性。
关键词：蛋形函数；弹塑性；屈服准则；非关联流动
Foundation item: Project(41672264) supported by the National Natural Science Foundation of China; Project (2019C03103) supported by the Key Research and Development Program of Zhejiang Province, China
Received date: 2020-01-15; Accepted date: 2020-06-07
Corresponding author: XU Ri-qing, PhD, Professor; Tel: +86-13606707291; E-mail: xurq@zju.edu.cn; ORCID: https://orcid.org/0000- 0002-9199-7330
Abstract: An exploratory discussion is presented on the application of egg-shaped function in elasto-plastic constitutive analysis for soft clay. Two main tasks of the paper are: 1) to propose a complete yield criterion based on egg-shaped function and supplement its definition in the deviatoric section, and then a yield criterion suitable for 3D stress conditions is obtained; 2) to elaborate its numerical implementation based on the drained triaxial tests. During the above discussion, a non-associated flow rule is proposed, in which the stress-dilatancy relationship in most classical theory is replaced by a linear dependence between the stress state parameter η and the rotation angle γ of the plastic potential surface. Thereafter, isotropic and kinematic hardening behavior is considered by employing the hardening parameter H, which can be expressed as the function of plastic work Wp. Finally, comparisons between numerical results and test data on Taizhou soft clay are made to verify the effectiveness of the proposed model.
