J. Cent. South Univ. (2012) 19: 459-464
DOI: 10.1007/s11771-012-1025-2
Particle swarm optimization based RVM classifier for non-linear circuit fault diagnosis
GAO Cheng(高成), HUANG Jiao-ying?(黄姣英), SUN Yue(孙悦), DIAO Sheng-long(刁胜龙)
School of Reliability and System Engineering, Beihang University, Beijing 100191, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract:
A relevance vector machine (RVM) based fault diagnosis method was presented for non-linear circuits. In order to simplify RVM classifier, parameters selection based on particle swarm optimization (PSO) and preprocessing technique based on the kurtosis and entropy of signals were used. Firstly, sinusoidal inputs with different frequencies were applied to the circuit under test (CUT). Then, the resulting frequency responses were sampled to generate features. The frequency response was sampled to compute its kurtosis and entropy, which can show the information capacity of signal. By analyzing the output signals, the proposed method can detect and identify faulty components in circuits. The results indicate that the fault classes can be classified correctly for at least 99% of the test data in example circuit. And the proposed method can diagnose hard and soft faults.
Key words:
1 Introduction
The advancement of nonlinear analog circuit diagnosis is not sufficient to satisfy contemporary requirements, especially for circuits with limited measurement accessibility [1-2]. Thus, there is a need for new effective method for fault classifier in nonlinear circuits [3].
It has been shown that classification accuracy is affected more by the choice of feature set than by the choice of classifier [4]. Pattern classification attempts to categorize measured data into limited output classes. Lots of modern classification methods were applied to circuit fault diagnosis, including Bayesian classifiers [5], hidden Markov models and artificial neural networks [6].
Classification problems were extensively studied. Numerous factors, such as incomplete data, and the choice of values for the parameters of given model, may affect classification results. Classification problems have been solved with statistical methods such as logistic regression or discriminating analysis. Technological advances have led to the development of methods for solving classification problems, including decision trees, backpropa-gation neural networks, rough set theory and support vector machine (SVM).
It is well known that artificial neural network (ANN) is good at tasks for pattern matching and classification due to its capability of learning from examples with both linear and nonlinear relationships between the input and output signals [7]. The extracted data as the network inputs without preprocessing were used [6, 8], which resulted in more complex networks and longer network training time. In order to further extend the ability of wavelet transform to represent complex patterns and reduce the computational burden of wavelet-based classification methods, a unique network called wavelet neural network (WNN) was proposed [9]. Using wavelet decomposition to preprocess the circuit impulse responses for training the neural networks was investigated recently. A neural network-based wavelet transformation method and a neural network-based L1-norm optimization approach were introduced in Ref. [6]. Usually, wavelet transform is a useful tool for data analysis, but in the real-time condition, such as on-line fault diagnosis, it is not practical for the complex computation. TAN et al [8] proposed a method for analog circuit diagnosis based on neural networks and Genetic algorithms. However, it requires sampling several accessible nodes data simultaneously, which makes data acquisition difficult because only the output terminal is accessible in most practical applications.
Support vector machine (SVM) [5, 10] based on statistics learning theory overcomes the insufficiency of neural network. It has many unique advantages, such as simple structure, global optimum, easy generalization and high dimension pattern recognition. Supporter vector machine is a set of related supervised learning methods used for classification and regression belonging to a family of generalized linear classifiers. However, SVM is not well suitable to diagnostic applications due to the lack of probabilistic outputs. The relevance vector machine (RVM) is a Bayesian form representing a generalized linear model of identical functional form to SVM. In addition to the probabilistic interpretation of output, it uses far fewer kernel functions for comparable performance [11-14].
If RVM is adopted without considering feature selection, then the dimension of input space is large and non-clean, which degrades the performance of the RVM. Particle swarm optimization (PSO) is a stochastic optimization technique. This work attempted to increase the classification accuracy rate by employing an approach based on PSO in RVM. Entropy and kurtosis were used as two feature parameters to identify the faulty modes based on RVM. Sinusoidal inputs with different frequencies were applied to the circuit under test (CUT), and the resulting frequency responses were sampled to generate the features. The frequency response data were sampled to compute its kurtosis and entropy, which can show the information capacity of signal.
2 RVM for classification
Relevance vector machine is a sparse probability model based on SVM proposed by TIPPING [5]. The training was carried out under Bayesian framework, so the distribution of predicted values was gotten by regression estimation with RVM. Compared with SVM, RVM has the following advantages:
1) With RVM, the probability forecasts can be obtained.
2) In inference process, subjective error in parameters setting can be avoided.
3) The number of relevant vectors used for training is less than that of SVM.
4) Since it need not satisfy the Mercer conditions, the choice for kernel function has a wide range.
The main difference between RVM and SVM is that RVM turns subjective division into objective division under probability, which makes classification function reach the maximum likelihood function for training set.
The output of RVM model is
(1)
where wi is the weight parameter needed to be determined; K(X, Xi) is a kernel function, effectively defining one basic function for each example in the training set.
In sparse model, the majority of 
are zero. The sparsity of model is based on a hierarchical prior, where an independent Gaussian prior is defined on the weight parameters in the first level:
(2)
where 
is the adjustment parameter of wi. Parameter 
is a vector consisting of N hyper parameters.
An iterative algorithm is used to estimate the weight. An independent Γ hyper prior is used for the variance parameters in second level:
(3)
where a and b are constants. The key point of this method is using the maximum of a posteriori (MAP) instead of maximum likelihood (ML) for weight estimation.
Given N pairs of training data 
the dataset likelihood is defined by applying the logistic sigmoid link function 
to y(X). Bernoulli distribution is used for P(t|X), then
(4)
where class label is denoted by t1
{0, 1}. Since the marginal likelihood distribution cannot be obtained by analytical method, the approximation method based on Laplace is used to estimate the hyper-parameter 
and weight parameters wi. The detailed algorithm is given in Ref. [15].
3 Parameters determination and pre- processing technique
3.1 PSO based parameters selection
Particle swarm optimization algorithm optimizes an object function by conducting population-based search. The population consists of potential solutions, called particles. These particles are randomly initialized and then freely fly across the multi-dimensional search space. During the flying, every particle updates its velocity and position based on the best experience of its own and entire population. The updating policy will drive the particle swarm to move toward region with higher object value, and eventually all particles will gather around the point with highest object value. The detail operation of PSO is given as follows.
Step 1: Initialization
The velocity and position of all particles are randomly set to within pre-specified or legal range.
Step 2: Velocity updating
The iterations and velocities of all particles are updated according to the following rule:
where pi and vi are position and velocity of particle i, respectively; pi,best and gbest are the position with best object value found so far by particle i and the entire population, respectively; w is a parameter controlling the dynamics of flying; R1 and R2 are random variables between 0 and 1; c1 and c2 are factors used to control the related weighting of corresponding terms.
The inclusion of random variables endows PSO with the ability of stochastic searching. The weighting factors, c1 and c2, compromise the inevitable tradeoff between exploration and exploitation.
After the updating, vi should be checked and clamped to pre-specified range to avoid violent random walking.
Step 3: Position updating
Assume that unit time interval between successive iterations and the positions of all particles are updated according to the following rule:
After the updating, the pi would also be checked and clamped to legal range to ensure legal solutions.
Step 4: Memory updating
Update pi,best and gbest when condition is meet.
If f(pi)>f(pi,best), pi,best←pi; if f(pi)>f(gbest), gbest←pi, where f(x) is the object function subject to maximization.
Step 5: Termination checking
Repeats Step 2 to Step 4 until certain termination condition is met. Once terminated, gbest and f(gbest) will be considered as the solution.
In this work, PSO was used to determine the parameters (ci, Ri) and feature selection for RVM. The flow chart is shown in Fig. 1.
3.2 Preprocessing technique
It is shown that classification accuracy is affected more by the choice of feature set than by the choice of classifier [16]. In order to simplify the RVM classifier, the preprocessing technique was used.
To extract features from an actual circuit output, kurtosis and entropy were used as feature parameters. Kurtosis is a measure of the heaviness of tails in distribution of signal x and can be used to establish an effective statistical test in identifying changes of signals [5]. Outlier or abrupt changes in x have high values and accordingly appear in the tails of the distribution. Consider x is the signal sampled from the accessible terminal of CUT and the probability density function (PDF) of signal x is px(x), then the j-th moment 
of x is defined by
(5)
Kurtosis is defined in the zero-mean case by
(6)
Fig. 1 PSO based parameters determination and feature selection approach for RVM
Entropy is a basic concept of information theory. Entropy H is defined for a discrete-valued random variable X as [15]
?? (7)
where ai are the possible values of X, P(X=ai) is the probability of X=ai. Depending on what the base of the logarithm is, different units of entropy are obtained.
The definition of entropy for a discrete-valued random variable can be generalized for continuous- valued random variables and vectors, often called differential entropy. The differential entropy H of a random variable x with density p(x) is defined as [17]
(8)
In order to simply the computation, the approximate maximum entropy of the signal can be simplified to
where k1 and k2 are positive constants, v is a random variable that meets the standard orthogonal distribution.
According to the above analysis, the kurtosis and entropy of signal through simple computation by selecting appropriate density functions can be obtained.
In this work, we will extract the output terminal response of CUT, x, as the original signal. The responses of CUT will have different feature parameters in different faulty modes. According to Eqs. (6) and (9), kurtosis kkurt(x) and entropy J(x) of extracted signal can be obtained.
4 Proposed method for fault diagnosis
Figure 2 shows the RVM method for diagnosing non-linear circuits fault. There are two major phases in Fig. 2: the training phase and the testing phase.
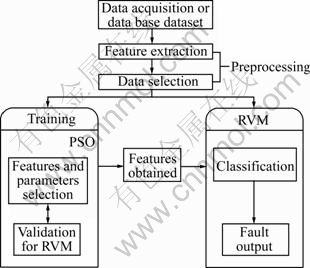
Fig. 2 Overall structure of proposed method for fault diagnosis
The Monte-Carlo analysis and parameter analysis were conducted to the CUT using Spice software and the simulation results were sampled from Spice for further signal processing in Matlab software. The detailed signal processing in Matlab is as follows.
Firstly, the maximum entropy of frequency response was extracted from CUT. According to Eq. (9), the entropy of the signal can be obtained when the two functions G1 and G2 are found. For computation reasons, considering function G1, the Gaussian function was chosen which can be considered as the log-density of a distribution with infinitely heavy tails (since it stays constant when going to infinity) for G2:
G2(x)=exp(-x2/2) (10)
For measuring asymmetry, there is
G1(x)=x·exp(-x2/2) (11)
According to Eq. (9), the entropy can be obtained as
(12)
where 
Then, according to Eq. (6), the kurtosis of signal can be obtained.
In this work, a negative mean absolute percentage error (MAPE) was used as the fitness function, expressed as [18]
(13)
where ai and di are the actual and diagnosis values, respectively; N is the number of diagnosis periods. Based on fitness functions, particles with higher fitness values are more likely to yield a smaller MAPE value. Once procedures were terminated, PSO reported the gbest and f(gbest) as its solution.
At the end of training stage, a set of features and parameters for a kernel function were obtained for the PSO-based RVM classifier. After training phase, the classifier was ready to be used to classify new fault frequency response in classification phase.
5 Experimental results
5.1 Sample circuit and faults
The circuit studied in this work was a non-linear rectifier circuit for converting an AC source to a DC source, as shown in Fig. 3. The considered fault classes include the hard faults caused by short-circuiting or open-circuiting D1, C1, C2 and C3, and the soft faults caused by changing the values of C2 and C3 ranging from 0 to 10 mF.
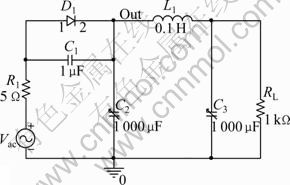
Fig. 3 Non-linear rectifier circuit
The resistors and capacitors were assumed to have tolerance of 5% and 10%, respectively. Frequency responses were used for this work. In fact, the same method can also be used in the time domain. When the value of a circuit component is higher (↑) or lower (↓) than its nominal value by 50% with the other components varying within their tolerances, a faulty frequency response was obtained. The faulty frequency responses will be reprocessed for feature selection and form the fault classes C2↑, C2↓, C3↑ and C3↓.
5.2 RVM initialization and train
In this work, 40 times Monte Carlo analysis of each condition were carried out and 440 fault samples altogether were obtained, which were divided into two groups. The half of samples were used to train RVM and the other half were used to test RVM classified ability.
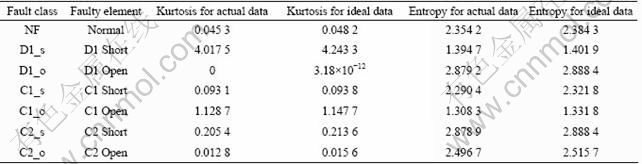
Table 1 Feature values for hard fault classes of non-linear rectifier circuit
At first, one to one mapping approach of RVM was used to train and classify fault sample. In training model, the Gaussian was chosen as kernel function. After initial value and parameter were initialed and training samples were used, the procedure renewed the parameter automatically with the Matlab7.0.
Scaling was applied to prevent feature values in greater numeric ranges from dominating those in smaller numeric ranges, and prevent numerical difficulties from the calculation. In general, the range of each feature value can be linearly scaled to the range [-1, +1].
5.3 Results and analysis
The experimental data of circuit without tolerance are listed in Table 1. It is shown that the values of the actual feature parameters are a little less than those of the simulation feature parameters, which is caused by the instrument readings having finite precisions and the values of elements changing in the real circuit. But we could still complete the fault dictionary correctly according to the actual acquisition data. Different fault classes fall into different groups based on the kurtosis and entropy of the extracted data, which means that these faults can be uniquely identified.
Figure 4 shows the soft fault classes of the nonlinear circuit when variable capacitors C1, C2 and C3 changed from 0 to 10 mF. The results are obtained by extracting the data 40 times through Monte-Carlo simulations for each capacitor being soft faulty by changing the values of the capacitors of the circuit. From Fig. 4, it can be seen that the soft faults of C1, C2 and C3 fall into different groups, which indicates that the method can be used to identify faults in nonlinear circuits as well.
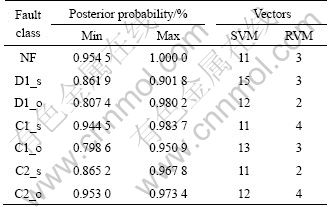
The detailed performance of this system in diagnosing the eleven fault classes associated with the nonlinear rectifier circuit indicates that all of the 40 test data for each class are classified correctly. Thus, it can be concluded that the proposed method can diagnose hard and soft faults. And all the fault classes can be classified correctely for at least 99% of the test data for our example circuit. Table 2 summarizes the classification performance of RVM compared with that of SVM on the same data sets. It can be seen that classification accuracy of RVM is comparable to that of SVM, but the number of relevant variable is much fewer than that of support vector. At the same time, the posterior probability of likelihood function can judge classification accuracy, and also may reject some mis-classification situation. This is RVM practical superiority in classification of fault diagnosis.
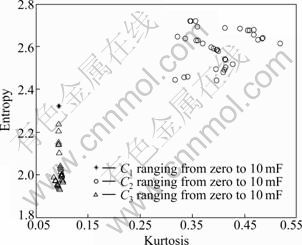
Fig. 4 Soft fault classes for nonlinear rectifier circuit with C1, C2 and C3 ranging from zero to 10 mF
Table 2 Comparison of classification performance between SVM and RVM
6 Conclusions
1) PSO-based RVM and higher-order statistical methods are applied to non-linear circuits fault diagnosis.
2) In order to simplify the RVM classifier, parameters selection based on PSO, preprocessing technique based on the kurtosis and entropy of signals are used. Entropy and kurtosis are used as the two feature parameters to identify the faulty modes based on RVM. The proposed scheme removes irreverent input features that may confuse the classifier and optimizes the kernel parameters simultaneously.
3) The classification performance of the RVM compared with that of SVM on the same data sets is summarized. It can be concluded that classification accuracy of RVM is comparable to that of SVM, but the number of relevant variables is much fewer than that of support vector.
4) Based on the RVM trained with the extracted kurtosis and entropy of signals as input feature parameters, the fault classes can be classified correctly for at least 99% of the test data for our example circuit.
References
[1] ARTUR R, ROMUALD Z. Fault diagnosis of analog piecewise linear circuits based on homotopy [J]. IEEE Transactions on Instruments and Measurement, 2002, 51(4): 876-881.
[2] LIU Qun-ying, LIU Qi-fang, HUANG Qi, LIU Jun-yong. Assessment of grid inherent vulnerability considering open circuit fault under potential energy framework [J]. Journal of Central South University of Technology, 2010, 17(6): 1300-1309.
[3] HUANG Jiun-lang, CHENG Wang-ting. Test point selection for analog fault diagnosis of unpowered circuit boards [J]. IEEE Transactions on Circuits and Systems-II: Analog and Digital Signal Processing, 2000, 47(10): 977-107.
[4] BIPLAB K, SIKDAR, GANGULY N, CHAUDHERI P P. Fault diagnosis of VLSI circuits with cellular automata based pattern classifier [J]. IEEE Transaction Computer-Aided Design Integration Circuits System, 2005, 24(7): 1115-1131.
[5] TIPPING M E. Sparse Bayesian learning and the relevance vector machine [J]. Machine Learning Research, 2001, 1(3): 211-344.
[6] HE Y, SUN Y. Neural network-based L1-norm optimisation approach for fault diagnosis of nonlinear circuits with tolerance [J]. IEEE Proceedings-Circuits, Devices and Systems, 2001, 148: 223-228.
[7] AMINIAN F, AMINIAN M, COLLINS H. Analog fault diagnosis of actual circuits using neural networks [J]. IEEE Transactions on Instruments and Measurement, 2002, 51(3): 544-560.
[8] TAN Yang-hong, HE Yi-gang, CUI Chun. A novel method for analog fault diagnosis based on neural networks and genetic algorithms [J]. IEEE Transactions on Instrumentation and Measurement, 2008, 57(11): 2631-2639.
[9] AMINIAN F, AMINIAN M. Neural-network based analog-circuit fault diagnosis using wavelet transform as preprocessor [J]. IEEE Transactions on Circuits and Systems-II: Analog and Digital Signal Processing, 2000, 47(2): 151-156.
[10] SAHA B, GOEBEL K, POLL S. Prognostics methods for battery health monitoring using a bayesian framework [J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(2): 291-296.
[11] XU Xiang-min, MAO Yun-feng, XIONG Jia-ni. Classification performance comparison between RVM and SVM [C]// Proceedings of IEEE International Workshop on Anti-counterfeiting, Security, Identification. 2007: 208-211.
[12] BABAEEAN A, TASHK A, BANDARABADI M. Target tracking using wavelet features and RVM classifier [C]// Fourth International Conference on Natural Computation. 2008: 569-572.
[13] TASHK A, SAYADIYAN, VALIOLLAHZADEH S. Face detection using adaboosted RVM-based component classifier [C]// Proceedings of 5th International Symposium on Image and Signal Processing and Analysis. 2007: 351-355.
[14] YANG Ying-tao, WANG Yue-gang, DENG Wei-qiang. Fault diagnosis in analog circuit based on RVM [C]// Proceedings of 2nd International Conference on Intellectual Technique in Industrial Practice. 2010: 634-637.
[15] SHEN Yue, LIU Guo-hai, LIU Hui. Classification method of power quality disturbances based on RVM [C]// Proceedings of the 8th World Congress on Intelligent Control and Automation. Ji’nan, China, 2010: 6130-6135.
[16] LIU Hong, CHEN Guang-ju, JIANG Shu-yan. A survey of feature extraction approaches in analog circuit fault diagnosis [C]// Pacific- Asia Workshop on Computational Intelligence and Industrial Application, 2008, 2: 676-680.
[17] YUAN Li-fen, HE Yi-gang, HUANG Jiao-ying, SUN Yi-chuang. A new neural network based fault diagnosis approach for analog circuits by using kurtosis and entropy as a preprocessor [J]. IEEE Transactions on Instruments and Measurement, 2010, 59(3): 586- 595.
[18] YANG Cheng-lin, TIAN Shu-lin, LONG Bing. Methods of handling the tolerance and test-point selection problem for analog-circuitfault diagnosis [J]. IEEE Transactions on Instruments and Measurement, 2011, 60(1): 176-185.
(Edited by DENG Lü-xiang)
Foundation item: Project(Z132012) supported by the Second Five Technology-based in Science and Industry Bureau of China; Project(YWF1103Q062) supported by the Fundemental Research Funds for the Central Universities in China
Received date: 2011-09-03; Accepted date: 2011-10-28
Corresponding author: HUANG Jiao-ying, PhD; Tel: +86-10-82314571; E-mail: huangjy@buaa.edu.cn
Abstract: A relevance vector machine (RVM) based fault diagnosis method was presented for non-linear circuits. In order to simplify RVM classifier, parameters selection based on particle swarm optimization (PSO) and preprocessing technique based on the kurtosis and entropy of signals were used. Firstly, sinusoidal inputs with different frequencies were applied to the circuit under test (CUT). Then, the resulting frequency responses were sampled to generate features. The frequency response was sampled to compute its kurtosis and entropy, which can show the information capacity of signal. By analyzing the output signals, the proposed method can detect and identify faulty components in circuits. The results indicate that the fault classes can be classified correctly for at least 99% of the test data in example circuit. And the proposed method can diagnose hard and soft faults.
