DOI: 10.11817/j.issn.1672-7207.2017.05.007
基于Rayleigh-Ritz法旋转薄壁圆盘行波特性分析
任红军1, 2,张景奇2,于晓光1,孙伟2
(1. 辽宁科技大学 机械工程与自动化学院,辽宁 鞍山,114051;
2. 大连理工大学 机械工程学院,辽宁 大连,116024)
摘 要:
实验测试与有限元仿真3种方法相互结合,分析中心固支条件的旋转薄壁圆盘的行波振动特性。基于Kirchhoff薄板基本假设,利用Lagrange方程,建立中心固支薄壁圆盘的能量方程。采用Rayleigh-Ritz法,利用多项式函数作为容许函数,建立旋转圆盘动力学分析的动力学方程,获得薄壁圆盘静止态固有特性和和旋转态行波特性的分析方法,并利用试验测试、有限元计算结果对本文所提出的解析方法进行验证。分析薄壁圆盘在静止态下的固有特性并对比分析不同旋转速度下旋转薄壁圆盘的行波特性。结果表明:前行波频率随转动速度增加而增加,后行波频率先减小后增加,当后行波频率减小为0时,前行波与后行波相互静止,即出现“驻波”现象,此时圆盘振动很容易引起共振破坏。
关键词:
薄壁圆盘;固有特性;行波振动特性;Rayleigh-Ritz法;
中图分类号:O326 文献标志码:A 文章编号:1672-7207(2017)05-1168-07
Travelling wave analysis of rotating thin disks via rayleigh-ritz method
REN Hongjun1, 2, ZHANG Jingqi2, YU Xiaoguang1, SUN Wei2
(1. School of Mechanical Engineering and automation, University of Science and Technology Liaoning, Anshan 114051, China;
2. School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China)
Abstract: The analysis method, experimental method and finite element method were imported to obtain the traveling wave vibration characteristics of the rotating disk with the center fixed. Based on the Kirchoff thin plates theory and Lagrange equation, the energy equations of the central fixed rotating disk were derived. Secondly, by taking the polynomial functions as the admission function, the Rayleigh-Ritz method was introduced to derive the dynamic equations of rotating disk, in which the characteristics of no-rotating disk and the traveling wave characteristics of rotating disk were considered at the same time. The results of the test and finite element analysis are verified by the proposed method of this paper. The natural characteristic of no-rotating disk and the traveling wave characteristics of rotating disk with different rotating speeds are calculated. The results show that the vibration mode of forward traveling wave increases gradually with rotating speed while the frequency of backward traveling wave decreases at first and then increases, the standing wave phenomena is produced and the disk is easily destroyed when the frequency of backward traveling wave equals zero.
Key words: thin disk; natural characteristic; travelling wave vibration characteristic; Rayleigh-Ritz method.
随着旋转机械装备向高性能、轻量化方向发展,大量轮盘类结构件,如燃气轮机的压气机轮盘、薄幅面齿轮等,具有薄壁结构特征,在高速旋转和复杂环境下容易产生振动,其后果往往是灾难性的,特别是由于局部共振所引起的高周疲劳破坏问题。因此,薄壁圆盘类关键结构件的行波振动特性研究具有重要的理论意义和应用价值。长期以来,科学工作者针对中心约束的旋转圆盘的振动特性开展了大量的研究并取得了丰富的理论结果。KOO[1]采用Rayleigh-Ritz法计算了复合材料旋转圆盘的极限频率问题。BUCHER[2]运用阵列传感器对旋转圆盘的行波现象和临界转速进行了测试。CHEN等[3]运用振动台测试了薄盘的轴向振动,通过扫频实验获得了圆盘的固有特性。PEI[4]运用解析法与仿真的方法结合,研究了转动速度对薄壁盘表面阻尼的影响。DODSON等[5]采用级数方法对中心完全夹紧的旋转圆盘方程进行了求解。在上述工作中,大多研究仅限于转速较低的与圆盘结构,对于圆盘的几何、材料参数及其行波动力学特性,如前、后行波频率等的讨论相对较少。KHORASANY等[6]运用经典解析理论,采用模态展开法,分析了薄壁圆盘的行波振动现象,并重点讨论了横向刚体运动对圆盘临界转速的影响。CHONAN等[7]运用经典薄板理论分析了圆盘振动的行波现象,并通过假设振型函数法,给出了中心固支旋转圆盘的振型函数,得到了Campbell图。由于工程背景的薄壁圆盘构件一般具有中心固支约束的边界条件,利用经典的弹性力学理论可以得到其振动特性,但是薄盘在一些特殊情况下会呈现大变形的非线性振动,这方面也引起了人们的重视[8-14]。本文作者针对旋转轮盘类构件动态特性分析的需求,将其简化为中心固支边界薄壁圆盘结构,开展旋转薄壁圆盘动力学建模以及行波特性分析。首先,基于Kirchhoff薄板基本假设,利用Lagrange方程,建立中心固支薄壁圆盘的能量方程。然后,利用Galerkin模态截断原理和基于Rayleigh-Ritz法的模态振型函数,获得旋转圆盘动态动力学方程和固有特性。采用有限元和试验测试对解析结果进行了验证。最后,分析了薄壁圆盘在静止态下的固有特性和在旋转态下的行波特性,给出了旋转圆盘共振Campbell曲线,为旋转圆盘构件设计分析提供支撑。
1 薄壁圆盘的动力学方程
假设薄壁圆盘为小挠度弯曲变形,基于Kirchhoff薄板理论建立薄壁圆盘的动力学方程。图1所示为薄盘的力学模型。如图1所示,设旋转坐标系为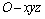 ,广义坐标系
,广义坐标系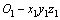 。薄壁圆盘的固定边界半径为a,自由边界半径为b,厚度为h。在旋转时,薄盘围绕z坐标轴旋转,转动角速度为
。薄壁圆盘的固定边界半径为a,自由边界半径为b,厚度为h。在旋转时,薄盘围绕z坐标轴旋转,转动角速度为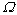 。取圆盘的一个微元体
。取圆盘的一个微元体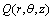 为研究对象进行力学分析,
为研究对象进行力学分析,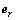 ,
,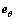 和
和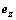 表示Q上的点在极坐标系下的单位速度矢量,即微元体的速度为
表示Q上的点在极坐标系下的单位速度矢量,即微元体的速度为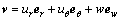 。
。
圆盘的弯曲势能为
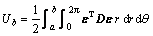 (1)
(1)
式中:中面的弯曲应变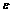 的元素为
的元素为
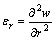 ,
,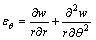 ,
,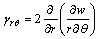 (2)
(2)
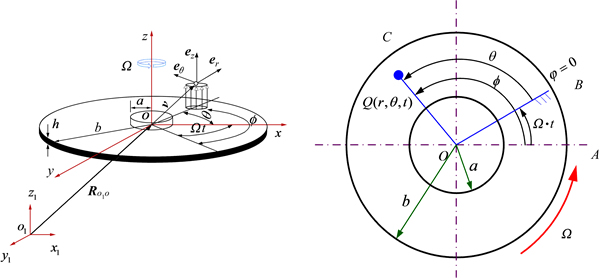
图1 薄盘的力学模型
Fig. 1 Mechanical model of rotating disk
D为弹性矩阵,表达式为
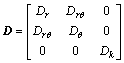 (3)
(3)
弹性矩阵D的各元素分别为
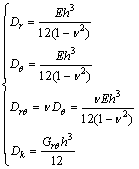 (4)
(4)
圆盘在以一定的角速度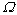 旋转时,微元体在径向和周向受到薄膜应力的作用。圆盘薄膜应力
旋转时,微元体在径向和周向受到薄膜应力的作用。圆盘薄膜应力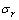 与
与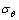 为:
为:
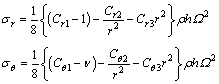 (5)
(5)
式(5)中各元素的表达式为:
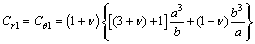
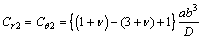
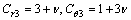
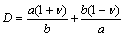 (6)
(6)
圆盘薄膜应力对应的势能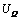 为
为
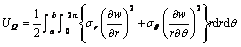 (7)
(7)
圆盘的动能为
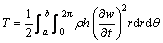 (8)
(8)
根据Galerkin截断原理,设圆盘振动控制方程为
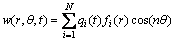 (9)
(9)
式中;N为截断的阶数(在此处代表节圆数);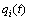 为振动位移关于时间t的函数;
为振动位移关于时间t的函数;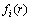 为关于半径r振型函数;n为节径数;
为关于半径r振型函数;n为节径数;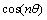 为圆盘振动振型谐波特性引入的余弦函数。
为圆盘振动振型谐波特性引入的余弦函数。
引入Lagrange函数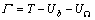 ,代入Lagrange方程
,代入Lagrange方程
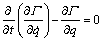 (10)
(10)
得到旋转圆盘动力学方程为
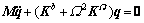 (11)
(11)
式中:q为位移向量;M为质量矩阵;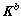 为圆盘刚度矩阵;
为圆盘刚度矩阵;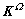 为离心力引起的刚度矩阵。
为离心力引起的刚度矩阵。
式(9)的解形式为
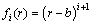 (12)
(12)
因此,式(11)中各矩阵的元素可计算得到。质量矩阵M的元素为
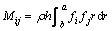 (13)
(13)
刚度矩阵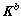 的元素表达式为
的元素表达式为
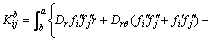

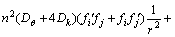
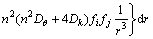 (14)
(14)
离心刚度矩阵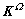 的元素的表达式为
的元素的表达式为
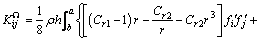
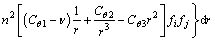 (15)
(15)
2 固有频率和行波频率的求解方法
设式(11)的自由振动解的形式为
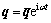 (16)
(16)
式中: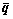 为振幅;
为振幅;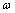 为固有频率。将式(16)代入式(11)中得到
为固有频率。将式(16)代入式(11)中得到
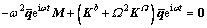 (17)
(17)
上式对应的特征值方程为
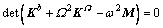 (18)
(18)
在静止坐标系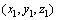 观察,转动态下的圆盘存在前行波与后行波,其相对于圆盘的速度等于波长与频率的乘积。通常地,将运动方向与圆盘转动方向相同的行波称为前行波,运动方向与圆盘转动方向相反的行波称为后行波。
观察,转动态下的圆盘存在前行波与后行波,其相对于圆盘的速度等于波长与频率的乘积。通常地,将运动方向与圆盘转动方向相同的行波称为前行波,运动方向与圆盘转动方向相反的行波称为后行波。
在圆盘坐标系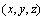 中,薄壁圆盘的振动方程解的形式为
中,薄壁圆盘的振动方程解的形式为
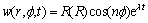 (19)
(19)
式中: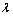 为整体坐标系
为整体坐标系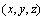 下圆盘的动频率。
下圆盘的动频率。
在广义坐标系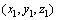 中,圆盘的动频率方程为
中,圆盘的动频率方程为
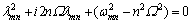 (20)
(20)
求解方程(20)得到旋转圆盘的行波频率为
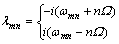 (21)
(21)
式中:m和n为圆盘振动的节圆数与节径数;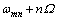 为圆盘的前行波频率(FTW);
为圆盘的前行波频率(FTW);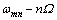 为圆盘的后行波频率(BTW);
为圆盘的后行波频率(BTW);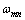 为圆盘的静频率。
为圆盘的静频率。
3 数值算例及结果讨论
根据上述旋转薄壁圆盘理论分析建模结果,可以进行薄壁圆盘在静止态和旋转态下的固有频率或行波频率的计算。为了对所提出的解析方法进行验证,分别采用锤击法测试静止态下薄壁圆盘的模态,采用有限元法测试静止态和旋转态下薄壁圆盘的模态,将所得结果与解析结果进行对比分析。其次,采用本文解析分析方法对旋转态薄壁圆盘行波特性进行分析,并与有限元法计算结果进行对比,讨论不同阶次行波频率受转动速度变化的影响规律。
本文采用的中心固支薄壁圆盘结构件如图2所示,其材料及几何参数如表1所示。
表1 薄壁圆盘的材料参考和几何参数
Table 1 Material and geometrical parameters of thin disk
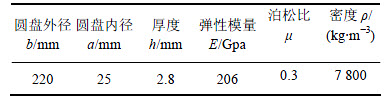
基于Ansys有限元软件建立薄壁圆盘有限元模型,采用Solid95建模,单元总数为600。薄壁圆盘约束条件为中心固支,采用的命令流是NSEL,S,LOC,X,r1。建立的薄壁圆盘有限元模型如图3所示。

图2 薄壁圆盘
Fig. 2 Photo of thin disk
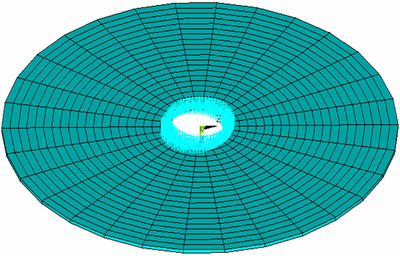
图3 薄壁圆盘的有限元模型
Fig. 3 FE model of thin disk
3.1 静止态下薄壁圆盘的模态计算结果
采用式(18)计算转动速度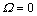 的工况即为静止态圆盘的固有频率。计算结果分别与有限元、实验测试进行对比,如表2所示。
的工况即为静止态圆盘的固有频率。计算结果分别与有限元、实验测试进行对比,如表2所示。
表2 静止态薄壁圆盘的固有频率结果对比
Table 2 Comparison of natural frequencies of disk in static condition
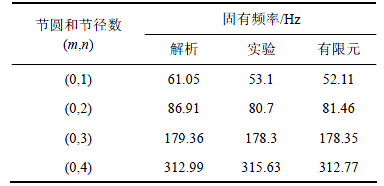
对比解析方法与试验测量结果,第(0,1)阶的相对误差为13%,第(0,2)阶的相对误差为7.14%,第(0,3)阶的相对误差为0.59%,第(0,4)阶的相对误差为0.843%。解析结果与有限元计算得到的固有频率相比,第(0,1)阶的相对误差为1.86%,第(0,2)阶的相对误差为0.94%,第(0,3)阶的相对误差为0.028%,第(0,4)阶的计算相对误差为0.906%。由此可见,本文解析方法具有较高的精度。
3.2 不同结构参数下薄壁圆盘振动特性分析
由于制造加工过程中,存在制造误差,薄壁圆盘的振动特性会与设计值产生偏差。这里重点讨论了薄壁圆盘的固有频率对其结构参数的敏感性。为了便于计算取薄盘厚度与半径比h/b分别为0.008,0.009,0.010,0.011,0.012,0.013,0.014,0.015,0.016和0.017,分析薄壁圆盘厚度与半径比值对其固有频率的影响,结果如图4所示,其中n为对应阶次。从图4可以看出:当半径保持不变时,厚度与半径的比与薄壁圆盘的固有频率成正比;随着比值的增加,薄壁圆盘的固有频率逐渐增大。
3.3 旋转态下薄壁圆盘的行波特性
在静止坐标(广义坐标)下,薄壁圆盘的振动表现出与转动坐标不同的振动形式,即行波现象。针对图1所示的分析对象,采用本文的解析方法、根据式(21)得到的解值绘制行波曲线,如图5所示。其中前行波用FTW表示,后行波用BTW表示,即(0,1)FTW表示第(0,1)振型前行波,(0,1)BTW表示第(0,1)振型后行波。

图4 不同厚度与半径之比h/b的固有频率
Fig. 4 Natural frequency of different h/b
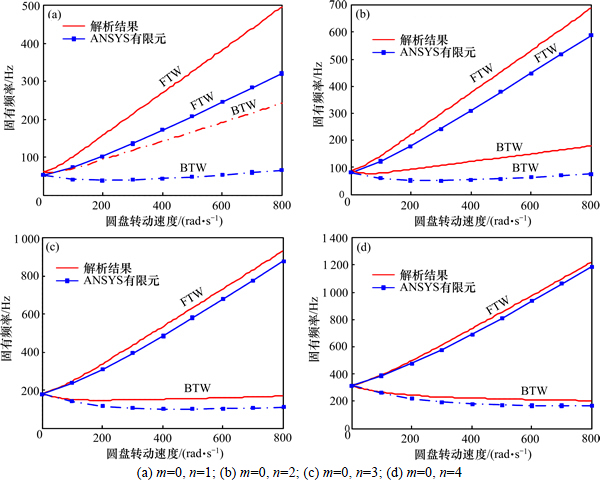
图5 薄壁圆盘的行波频率的解析结果与有限元计算结果
Fig. 5 Vibration of bifurcation of frequency as a function of rotating speed
由图3可以看出:前行波频率随转动速度增加而增加,后行波频率先减小后增加,当后行波频率减小为0时,广义坐标系下观察前行波与后行波相互静止,即出现驻波现象,此时的圆盘振动很容易引起破坏。圆盘的后行波频率(0,3)BTW随转动速度变化,与速度轴并没有产生交点,说明圆盘的动频系数大于3。
本文解析方法得到的行波曲线与利用有限元计算得到的行波曲线进行对比,结果如图3所示。由图3可以看出:第(0,3)阶与(0,4)阶的行波振动图,解析计算与有限元结果能够很好地吻合。而第(0,1)阶和(0,2)阶的行波曲线偏差较大,这与所采用的Rayleigh-Ritz法假设的振型函数有关。
3.4 不同厚度比对行波特性影响
实际加工中,由于存在制造加工误差,圆盘会出现尺寸偏差,因此对尺寸偏差对行波特性的影响具有重要的价值。本文中,研究不同厚度与长度比H/L下行波特性,其中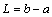 ,为了简化计算,仅选取H/L=0.1与H/L=0.2这2种工况分析,结果如图4所示,其中前行波用FTW表示,后行波用BTW表示。图6所示为不同厚度比薄壁圆盘的行波频率。由图6可以看出:不同长厚比下的圆盘前行波频率随转动速度增加而增加,后行波频率先减小后增加。随着厚度比增加,圆盘的固有频率增加,第(0,1)阶模态受长厚比影响最大,其余阶次影响较小。可以得出高阶振动模态对尺寸误差不敏感。
,为了简化计算,仅选取H/L=0.1与H/L=0.2这2种工况分析,结果如图4所示,其中前行波用FTW表示,后行波用BTW表示。图6所示为不同厚度比薄壁圆盘的行波频率。由图6可以看出:不同长厚比下的圆盘前行波频率随转动速度增加而增加,后行波频率先减小后增加。随着厚度比增加,圆盘的固有频率增加,第(0,1)阶模态受长厚比影响最大,其余阶次影响较小。可以得出高阶振动模态对尺寸误差不敏感。
4 结论
1) 采用实验与有限元结合的方法,对本文的解析算法进行模态对比确认,证明了本文计算方法的合理性,对不同结构参数下薄壁圆盘振动特性进行分析,得知厚度与半径的比值与薄壁圆盘的固有频率成正比关系。
2) 分析了转动态下圆盘的固有频率变化和行波特性,结果表明前行波频率随转动速度增加而增加,后行波频率先减小后增加,当后行波频率减小为0时,前行波与后行波相互静止,即出现“驻波”现象,此时圆盘振动很容易引起共振破坏。圆盘结构参数对低阶固有频率有明显的影响,高阶振动模态对结构参数敏感性较小。
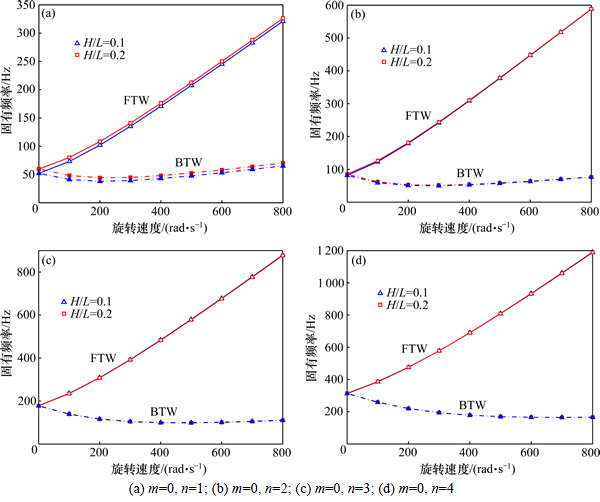
图6 不同厚度比薄壁圆盘的行波频率
Fig. 6 Traveling wave of rotating disks with different thickness ratios
3) 本文采用的方法不必分析旋转圆盘具体应力变化过程,只计算运动过程中的动能与弯曲势能,运算效率更高,适合复杂工况下的圆盘动力学特性分析。
参考文献:
[1] KOO K N. Vibration analysis and critical speeds of polar orthotropic annular disks in rotation[J]. Composite Structures, 2006, 76(1): 67-72.
[2] BUCHER I. Transforming and separating rotating disk vibrations using a sensor array[J]. Journal of Sound and Vibration, 2011, 330(6): 1244-1264.
[3] CHEN J S, FANG Y Y. Warping of stationary and rotating heavy disks[J]. International Journal of Solids & Structures, 2011, 48(21): 3032-3040.
[4] PEI Y C. Thermoelastic damping in rotating flexible micro-disk[J]. International Journal of Mechanical Sciences, 2012, 61(1): 52-64.
[5] DODSON JR R O, EVERSMAN W. Free vibration of a centrally clamped spinning circular disk[J]. AIAA Journal, 1969, 7(10): 2010-2012.
[6] KHORASANY R M H, HUTTON S G. An analytical study on the effect of rigid body translational degree of freedom on the vibration characteristics of elastically constrained rotating disks[J]. International Journal of Mechanical Sciences, 2010, 52(9): 1186-1192.
[7] CHONAN S, MIKAMI T, ISHIKAW H. The vibration and critical speeds of rotating sawblades[J]. Proceedings of JSME, 1986, 52: 1805-1812.
[8] NOWINSKI J L. Nonlinear transverse vibrations of a spinning disk[J]. Journal of Applied Mechanics, 1964, 31(1): 72-78.
[9] JANA A, RAMAN A. Aeroelastic flutter of a disk rotating in an unbounded acoustic medium[J]. Journal of Sound and Vibration, 2006, 289(3): 612-631.
[10] NAYFEH A H, JILANI A, MANZIONE P. Transverse vibrations of a centrally clamped rotating circular disk[J]. Nonlinear Dynamics, 2001, 26(2): 163-178.
[11] LUO A C J. An approximate theory for geometrically nonlinear thin plates[J]. International Journal of Solids and Structures, 2000, 37(51): 7655-7670.
[12] LUO A C J, MOTE C D. Nonlinear vibration of rotating thin disks[J]. Journal of Vibration and Acoustics, 2000, 122(4): 376-383.
[13] PEI Y C, HE L, WANG J X. Rotating flexible disk under shaft temperature increment[J]. Journal of Sound and Vibration, 2010, 329(17): 3550-3564.
[14] YI Y B. Finite element analysis of thermoelastic damping in contour-mode vibrations of micro and nanoscale ring, disk, and elliptical plate resonators[J]. Journal of Vibration & Acoustics, 2010, 132(4): 1154-1174.
(编辑 陈爱华)
收稿日期:2016-07-11;修回日期:2016-09-25
基金项目(Foundation item):国家自然科学基金资助项目(11472068) (Project(11472068) supported by the National Natural Science Foundation of China)
通信作者:于晓光,博士,教授,从事机械振动监测及故障诊断研究;E-mail: yuxiaoguang58@163.com
摘要:采用理论分析、实验测试与有限元仿真3种方法相互结合,分析中心固支条件的旋转薄壁圆盘的行波振动特性。基于Kirchhoff薄板基本假设,利用Lagrange方程,建立中心固支薄壁圆盘的能量方程。采用Rayleigh-Ritz法,利用多项式函数作为容许函数,建立旋转圆盘动力学分析的动力学方程,获得薄壁圆盘静止态固有特性和和旋转态行波特性的分析方法,并利用试验测试、有限元计算结果对本文所提出的解析方法进行验证。分析薄壁圆盘在静止态下的固有特性并对比分析不同旋转速度下旋转薄壁圆盘的行波特性。结果表明:前行波频率随转动速度增加而增加,后行波频率先减小后增加,当后行波频率减小为0时,前行波与后行波相互静止,即出现“驻波”现象,此时圆盘振动很容易引起共振破坏。


