基于柔性步行路径的双足步行机器人步态参数分析
陆荣信,陈建芳,冯朝,肖晓晖,徐俊,吴怡
(武汉大学 动力与机械学院,湖北 武汉,430072)
摘 要:
行路径间的刚柔耦合模型,分析路径参数对机器人步态参数的影响规律。首先,采用基于自然零力矩点(ZMP)轨迹的步态规划方法,通过给定参考ZMP轨迹获取机器人质心轨迹,插值得到机器人在刚性路径下的步态;其次,基于Pasternak地基模型,在ANSYS中建立公路的多层柔性模型,导入ADAMS中与机器人多刚体模型耦合。通过3组柔性参数与理想刚性路面假设下的步行仿真,分析地面的柔性参数对机器人质心与ZMP轨迹、关节驱动力矩等参数的影响。研究结果表明:机器人在柔性地基公路上步行时质心高度比较稳定,波动小于2.6%,质心沿前进方向移动距离接近预期规划的步行距离,比刚性路径假设下的步行效率高;驱动力矩变化趋势与刚性路径变化趋势基本一致,其中支撑腿相应关节的驱动力矩突变峰值减少8.3%~33.4%,关节运动更平稳;足底接触力较刚性路径波动范围增大7.2%~16.7%,地面对机器人的冲击减少约8.0%。在自然柔性地面环境中,双足步行机器人的步态效率更高,运动更平稳。
关键词:
双足步行机器人;步态规划;柔性路径;Pasternak模型;刚-柔耦合;
中图分类号:TM8; TM113 文献标志码:A 文章编号:1672-7207(2014)10-3443-07
Gait parameters analysis of biped walking robot based on flexible walking path
LU Rongxin, CHEN Jianfang, FENG Zhao, XIAO Xiaohui, XU Jun, WU Yi
(College of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China)
Abstract: A rigid-flexible coupling model between biped robot and its walking path was established to analyze the influence of path parameters on gait parameters. Firstly, with the method of gait planning based on natural ZMP trajectory, robot centric track was obtained by setting reference of ZMP trajectory, and then the gait on a rigid path was acquired by interpolation. Secondly, multilayer flexible model of road was established in ANSYS software based on Pasternak foundation model to be exported to ADAMS and coupled with the robot multi-rigid-body model, then the effect on mass trajectory, centric trajectory and driving torque of joint from flexibility data of ground were analyzed by simulating the robot walking in three groups of flexible surface and one ideal rigid surface. The results show that the height of mass center is more stable with fluctuation being less than 2.6%, moving distance along the forward direction is much closer to prospective walking distance and the walking efficiency on a flexible path is higher than that on a rigid path. Although the trend of driving torque is similar to that in a rigid path, its mutation peak in the joints on supporting leg is reduced by 8.3%-33.4%, and so the joint can move more steadily. Moreover, the fluctuation range of pelma contact force is 7.2%-16.7% more than that in the rigid path, and the impact from the ground upon the robot is reduced by 8.0%, which indicates that the biped robot is capable of walking most efficiently in natural ground environment.
Key words: biped robot; gait planning; flexible path; Pasternak model; rigid-flexible coupling
步行机器人在自然真实环境中的步态稳定性和步行效率是其走向应用的关键之一。步态是机器人步行过程中各关节在时序和空间上的协调关系,是双足步行机器人稳定步行的基础。然而,目前人们对于双足步行机器人的运动规划大多是假设地面为理想刚性,忽略了步行路径的黏弹性对机器人步态参数的影响。双足机器人步态规划方法主要有2类:基于人类步行数据(HMCD)的仿生方法[1]和基于稳定性的规划方法,后者最典型的是基于零力矩(zero-moment point,简称ZMP)稳定判据的步态规划方法[2]。Dasgupta[3]采用基于ZMP的方法进行步态规划研究。王志良等[4]进行了基于ZMP判据的机器人步行模式与步态规划研究。针对在自然地面环境下的步行问题,Kajita等[5]研究不平整地面的双足步行机器人动态步行控制,采用线性倒立摆模型及能量守恒概念生成全局变量;Fujimoto等[6]通过设计摆动足和双足步行机器人质心轨迹求解步态,将双足步行机器人的质心看作是线性倒立摆,摆动腿末端的运动轨迹用连接2个采样时间的落地点的平滑函数来表示。但以上工作都忽略了步行路径的柔性。针对机器人与作业路径间的耦合动力学分析,付宜利等[7]研究了沙地步行机器人的驱动车轮及附属装置,提出了刚性和柔性的有机结合是合理的分析方法;Lacagnina等[8]对火山探测机器人的多体动力学仿真,考虑了6个步行轮与地面间接触耦合特性。Xiao等[9]研究了轮式机器人在沿柔索作业过程中其滚动、过障、姿态调整时与柔性架空导线间耦合动力学特性。可见,国内外研究双足步行机器人步态规划与动力学时,尚未系统分析地面黏弹性对机器人关节的动态响应特性和步行稳定性的影响,为此,本文作者研究考虑地面柔性的步行路径模型,建立机器人-地面间的刚柔耦合模型,分析步行路径的柔性参数对机器人步行时的关节动态响应特性、质心轨迹、步态稳定性的影响规律。
1 基于刚性路径假设的双足步行机器人步态规划
稳定步行是双足步行机器人执行各种作业任务的前提条件。在研究自然地面环境下的步态规划之前,先假设步行地面为理想刚性,机器人为多刚体,采用Takanishi等[10]提出的基于期望ZMP的方法进行双足步行机器人步态规划。
1.1 基于ZMP判据的双足步行步态规划基本思想
ZMP点见图1。ZMP最初由Vukobratovic等提出[12],指机器人足底分布的反力等效合力R通过足底的作用点(见图1(a)中A点),即机器人的重力补偿力Mg和惯性力Fa两者合力与地面的交点[11](见图1(b))。
机器人足底与地面间所有接触点的最小多边形区域称为支撑多边形,见图 2中的灰色区域。单腿支撑期时为单个足掌,双腿支撑期时为 2只支撑足接触点最外缘分布的点围成的最大凸多边形,在数学上定义为这些接触点集合的最小凸集或凸包。在高速步行时,惯性力使机器人重心在水平面的投影与ZMP不能始终重合,步行时保持ZMP在支撑多边形之内,则支撑足掌与地面保持相对静止,不可能发生翻转等失稳现象,这就是ZMP稳定判据[2]。将ZMP与支撑多边形边界的最短距离作为系统的稳定裕度。
双足步行机器人的步态规划即为规划步行过程中的各关节运动轨迹,如足掌离地时间、各关节的运动情况等。现采用基于期望ZMP的步态规划方法,其基本思路为:基于预先规划ZMP轨迹求解质心轨迹;其次,通过正运动学得到关节运动轨迹;通过逆运动学求解各关节角轨迹。
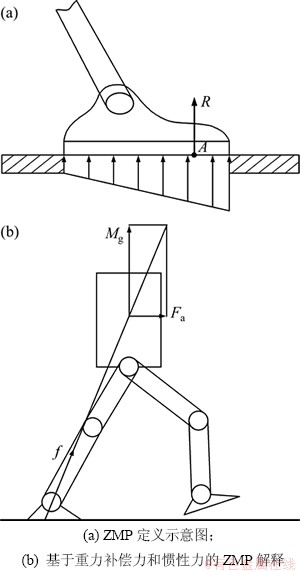
图1 ZMP点
Fig. 1 Zero-moment point
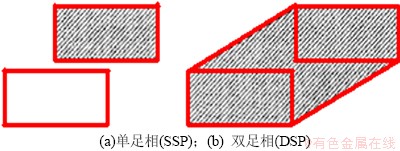
图2 支撑多边形
Fig. 2 Supported polygon
1.2 基于刚性路径假设的机器人步态规划
1.2.1 ZMP的规划和质心轨迹的数值求解
ZMP轨迹要满足在支撑图形的中间,ZMP距离支撑图形的边界越远,对于步行的机器人来说,步行的稳定裕度越高。1个规划好的供机器人步行参照的ZMP轨迹通常称为基准ZMP,如图3中的ZMP_ref。
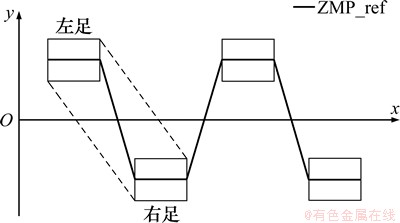
图3 基准ZMP规划示意
Fig. 3 ZMP-based gait planning
图3中标示的左足为左单足相阶段,ZMP轨迹保持在足的中间,当右足触地时,则进入双足相。ZMP从左足的足尖运动到右足的足跟,此支撑图形是图中虚线和2个足组成的凸多边形,这种规划是比较接近人类的步行的。其中,通过模型简化以及求解后可得到质心轨迹与预先规划的ZMP轨迹的关系式:
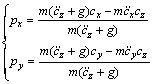 (1)
(1)
式中:px和py分别为ZMP点的X和Y方向坐标;cx,cy和cz分别为质心的X,Y和Z方向坐标;m为机器人等效质量。
根据式(1),调整稳定裕度的部分设计可调整参数,如图4所示。在起步阶段,ZMP轨迹在Y向移动到左足位置,机器人初始姿势直立,此时机器人不受惯性力作用,ZMP点与质心重合,即图4中(0, 0)点。机器人在进入初始步行状态时也需要保持ZMP在支撑图形内,当机器人进入步行状态时,缩小ZMP的Y向距离,减少上身运动。针对所述规划的ZMP轨迹生成的质心轨迹如图5所示。
1.2.2 足部轨迹的插值
基于期望ZMP进行足部插值,设置参数如图6所示。图6中:Ds为步长;θ1和θ2分别为足抬起和下落时足底和地面夹角;b1和b2分别为足以踝关节为分界的2部分足长;L1和L2分别为大腿和小腿的长度。
推导髋关节运动轨迹方程如下:
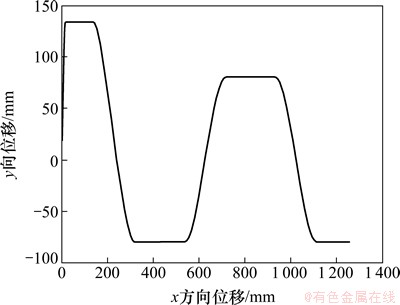
图4 基准ZMP轨迹
Fig. 4 Reference ZMP trajectory
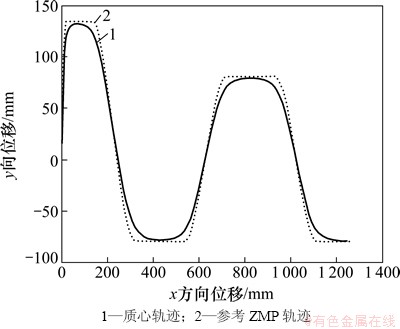
图5 ZMP离散化求质心轨迹的X-Y曲线
Fig. 5 ZMP trajectory discretization seeking centroid curve of X-Y
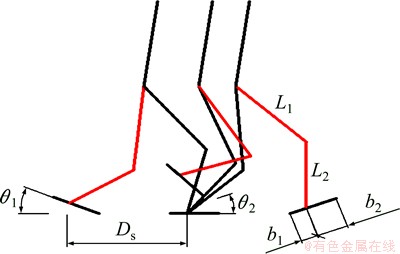
图6 足部插值参数
Fig. 6 Foot interpolation parameters
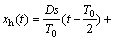
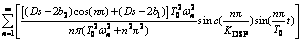
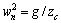 (2)
(2)
式中:T0为步行周期;KDSP为双足相时间参数。设各对应的坐标符号分别为:髋关节(xh,zh),膝关节(xk1,zk1)和(xk2,zk2),踝关节(xa1,za1)和(xa2,za2),得到模型几何约束方程:
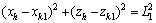
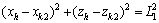
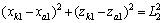
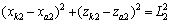 (3)
(3)
通过设置上述参数,编制足部的插值函数,得到图7所示足部轨迹。在Y方向上,足部的轨迹配合ZMP向距离减小过渡。
编制足部插值函数的基本方法是对1个步行周期中几个状态的插值,然后,把几个状态综合在一起,在双、单足相的时间和位移上和ZMP轨迹配合,插值函数给出的是1个时间段内的2个足部的位姿、速度、角速度等信息。
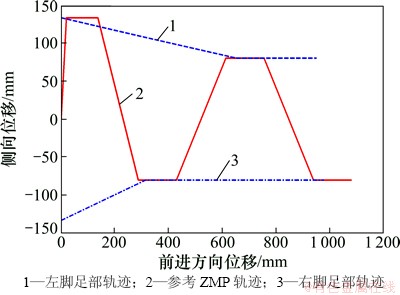
图7 左、右足插值函数和基准ZMP的X-Y曲线
Fig. 7 Left foot interpolation function and reference ZMP curve of X-Y
2 基于步行路径-机器人刚柔耦合模型的双足步态分析
为了提高机器人对真实环境的适应能力、步态稳定性及步行效率,对步行机器人运动进行规划时,应考虑在真实环境中与地面形成的时变非线性动力学耦合及其对质心轨迹、步态稳定性的影响。本文以室外沥青路面为步行路径,建立双足步行机器人与柔性路径间的耦合动力学模型,研究地面参数对机器人关节动态响应、步态参数的影响。
2.1 柔性路径的动力学建模
在ADAMS中,有3种建立柔性体的方法:1) 柔性梁连接法;2) 有限元法;3) 运用ADAMS/AutoFlex模块,直接在ADAMS/ View中建立柔性体的MNF文件,然后再用柔性体代替原来的刚性体。现选用有限元软件ANSYS建立柔性路径。
以沥青路面为对象,建立其有限元模型时,有2种方案:
1) 板模型。将公路面层看作受到地基支承的单块或多块板,地基可采用Winkler模型、弹性半空间模型或Pasternak模型,对板的支承都等价作用于单元节点上的反力。路面板可分为单层或双层。
2) 三维模型。考虑路面结构的实际几何形状、结构层次、接缝或裂缝影响和荷载作用位置,是比较理想的模型,但需要较大的计算内存,计算量大。由于研究重点在于机器人的步行,因此,采用较简单的板模型来模拟路面。路面和路基用双层薄板模拟,上层板代表路面层,下层板代表路基层,如图8中的层面1和2。地基采用Pasternak模型,路面结构的物理特性用厚度、密度、弹性模量和泊松比表示。
相对于面层的宽度方向,基层在水平方向无限大,地基在水平和纵向无限大。而采用有限元模拟时,用有限区域来描述模型,用10节点四面体单元SOLID92进行网格划分。
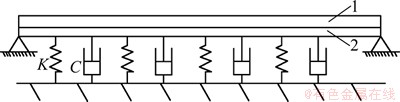
图8 沥青公路的动力学模型
Fig. 8 Dynamic model of asphalt road
2.2 步行路径-机器人刚柔耦合模型
将柔性体导入ADAMS中,针对机器人足底与柔性地面的接触力,通过创建虚构件(dummy part)与柔性体固接,建立虚构件与其他构件之间的连接关系。所建立的机器人-步行路径耦合模型如图9所示。
2.3 基于步行路径-机器人刚柔耦合模型的双足步行仿真
根据JTGD 50—2006《公路沥青路面设计规范》选取路面参数。为了考察步行路径的柔性参数对机器人步态的影响,通过设置3组不同参数(见表1)的路面弹性板结构进行对比分析。
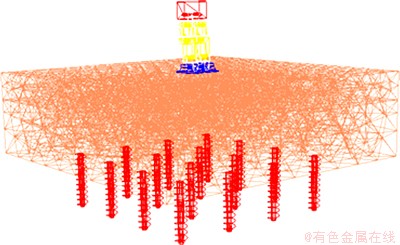
图9 步行路径-机器人刚柔耦合模型
Fig. 9 Robot-walking path coupling model
基于前述采用期望自然ZMP轨迹得到的步态规划参数,仿真得到质心位移-时间历程、ZMP轨迹,膝关节驱动力矩和足底接触力等响应特性参数,分别见图10~13。
表1 沥青路面弹性模量
Table 1 Elastic module of asphalt pavement MPa

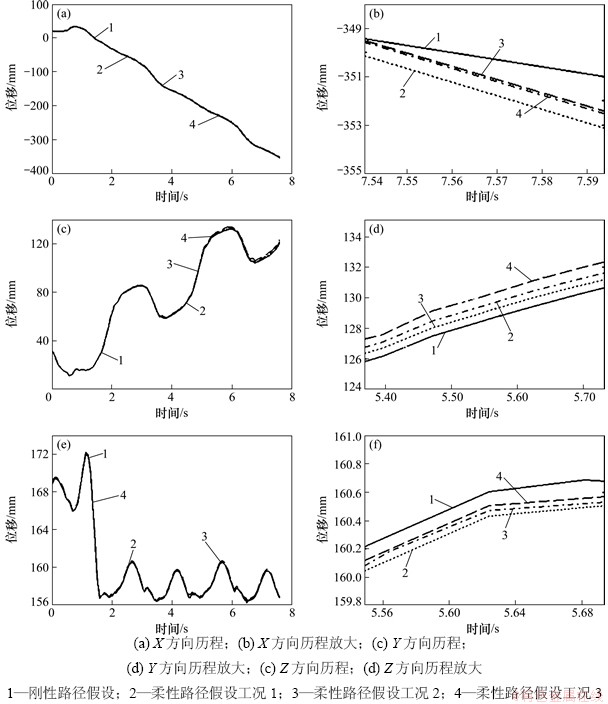
图10 质心位移-时间历程曲线
Fig. 10 Centroid displacement-time curves
3 柔性路径对机器人步行参数的影响规律
3.1 柔性路径对机器人质心轨迹的影响
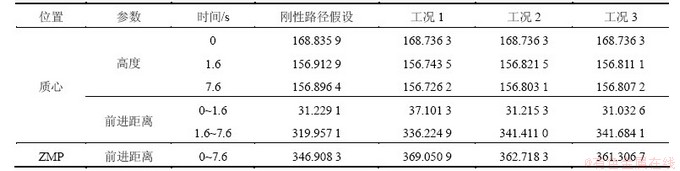
对比分析3组柔性路径参数与刚性假设下的质心轨迹见图10。表2所示为3种工况下3个时间点的质心高度和2个时间段内质心沿前向的移动距离。通过分析可知:在柔性作业路径中,给定机器人的运动目标函数,各关节均能实现稳定运动,这表明已建立的双足步行机器人与柔性路径间的耦合动力学模型是有效的。具体分析如下。
在柔性作业路径中,机器人质心在高度方向能保持稳定,但因地面产生形变,相对于刚性路径质心高度有所降低,稳定步行阶段质心高度波动均小于2.6%,并在柔性路径中,预期规划的前行距离为360.0 mm,机器人沿前向移动的距离分别为373.3,372.6和372.7 mm,而在刚性路径中前向移动的距离为351.1 mm,说明在自然地面环境下,机器人的步行效率更高。
3.2 柔性路径对机器人ZMP轨迹的影响
图11所示为ZMP轨迹。在柔性作业路径中,机器人的实际ZMP轨迹与期望ZMP趋势一致,能够实现步行稳定。3种工况下ZMP前向移动距离见表2。从表2可见:在考虑路径柔性时,ZMP移动距离较刚性路径假设时高4.2%~6.8%,说明自然地面环境下,机器人的步态效率更高。
3.3 柔性路径对机器人驱动力矩的影响
图12所示为驱动力矩曲线。从图12可见:在柔性作业路径中,机器人关节驱动力矩时程曲线的趋势与刚性路径时基本一致;当下肢处于支撑状态时,足底与柔性地面的冲击较小,驱动力矩出现突变峰值减少8.3%~33.4%,说明在自然地面环境下,机器人的步态更平稳。
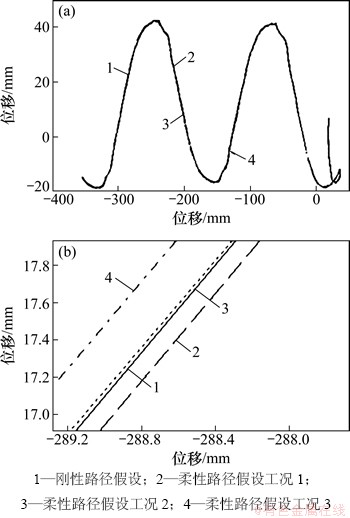
图11 ZMP轨迹
Fig. 11 ZMP trajectories
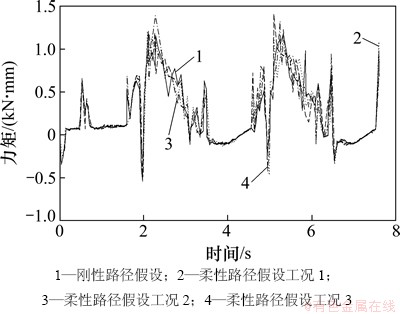
图12 膝关节驱动力矩-时间历程曲线
Fig. 12 Driving moment-time curves of knee joint
表2 质心与ZMP参数统计
Table 2 Gait parameter of COM and ZMP mm
3.4 柔性路径对机器人足底接触力的影响
图13所示为足底接触力曲线。从图13可见:在柔性作业路径中,足底接触力较刚性路径中波动大,波动范围为7.2%~16.7%;同时,因柔性地面相对于刚性地面考虑了阻尼系数,吸振能力强,机器人在步行过程冲击峰值减少了约8.0%。
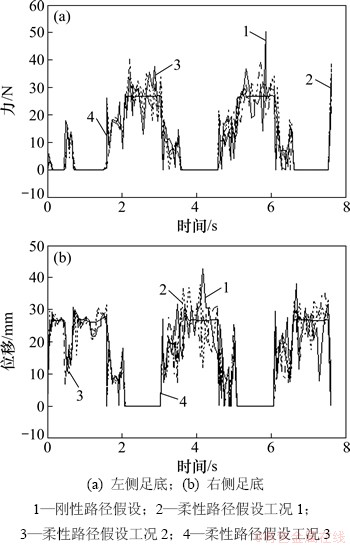
图13 足底接触力-时间历程曲线
Fig. 13 Contact force-time curves of foot plate
4 结论
1) 基于Pasternak地基模型,通过ANSYS软件建立了几种不同参数属性的柔性地面模态中性文件,导入ADAMS中得到机器人与柔性地面间的耦合动力学模型,加载基于自然零力矩点(ZMP)轨迹的步态规划方法得到的步态数据,在三组柔性参数与理想刚性路面工况下对机器人进行了动力学仿真。在柔性路径作业下,机器人具有更高的步行效率,机器人质心和ZMP比期望前进距离远3.3%~3.7%,而刚性路径作业下机器人质心和ZMP比期望前进距离近2.4%。
2) 在柔性路径作业下机器人具有更加稳定的步态:柔性作业路径下机器人机器人驱动力与足底接触力比刚性路径作业下支撑腿相应关节的驱动力矩突变峰值减少8.3%~33.4%,足底接触力较刚性路径波动范围增大7.2%~16.7%,地面对机器人的冲击减少约8.0%,质心波动小于2.6%。
3) 为了提高步行效率,需对真实路径下的步态稳定性进行进一步研究。
参考文献:
[1] 包志军. 仿人型机器人运动特性研究[D]. 上海: 上海交通大学, 2000.
BAO Zhijun. Research on the movement characters of humanoid robot[D]. Shanghai: Shanghai Jiao Tong University, 2000.
[2] Vukobratovic M, Brovac B. Zero-moment point-thirty five years of its life[J]. Journal of Humanoid Robotics, 2004, 1(1): 157-173.
[3] Dasgupta A, Nakamura Y. Making feasible walking motion of humanoid robots from human motion capture data[C]//IEEE International Conference on Robotics and Automation. Detroit, USA, 1999: 1044-1049.
[4] 王志良, 于国晨, 解仑. 基于解耦合成的及ZMP方程的仿人机器人三维步态规划[J]. 计算机科学, 2010, 37(12): 215-217.
WANG Zhiliang, YU Guochen, XIE Lun. Three-dimensional gait planning for humanoid robots based on decoupling synthesis and ZMP algorithm[J]. Computer Science, 2010, 37(12): 215-217.
[5] Kajita S, Nagasaki T, Kaneko K, et al. A running controller of humanoid biped HRP-2LR[C]//Proceedings of the 2005 IEEE International Conference on Robotics and Automation. Barcelona, Spain, 2005: 616-622.
[6] Fujimoto Y, Smadi I A, Wakayama Y. Development of musculoskeletal biped robot driven by direct-drive actuators[C]//Mechatronics (ICM), 2011 IEEE International Conference. 2011: 821-826.
[7] 付宜利, 徐贺, 王树国, 等. 沙地环境移动机器人驱动轮的发展概况综述[J]. 机器人技术与应用, 2004, 4: 22-29.
FU Yili, XU He, WANG Shuguo, et al. Summary of the development of driving wheel of sandy environment for mobile robot[J]. Robot Technique and Application, 2004, 4: 22-29.
[8] Lacagnina, Michele, Muscato, Giovanni, Sinatra, Rosario. Modeling and simulation of multi-body mobile robot for volcanic environment explorations[C]//IEEE International Conference on Intelligent Robots and Systems. EPFL, Switzerland, 2002: 714-720.
[9] XIAO Xiaohui, WU Gongping, DU E, et al. Impacts of flexible obstructive working environment on dynamic performances of inspection robot for power transmission line[J]. Journal of Center South University of Technology, 2008, 15(6): 869-876.
[10] 姚世斌. 双臂手移动机器人地面步行的研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2009.
YAO Shibin. Research on dual-arm & hands mobile robot walking on the ground[D]. Harbin: Harbin Institute of Technology. School of Mechanical Engineering, 2009.
[11] 梶田秀司. 仿人机器人[M]. 管贻生, 译. 北京: 清华大学出版社, 2007: 10-150.
Shuuji Kajita. Humanoid robot[M]. GUAN Yisheng, trans. Beijing: Tsinghua University Press, 2007: 10-150.
(编辑 陈灿华)
收稿日期:2013-10-31;修回日期:2013-12-22
基金项目(Foundation item):国家自然科学基金资助项目(51175383)(Project (51175383) supported by National Natural Science Foundation of China)
通信作者:肖晓晖(1969-),女,湖南安化人,博士,教授,博士生导师,从事移动机器人学与微操作机器人研究;电话:13720360269;E-mail:xhxiao@whu.edu.cn
摘要:建立机器人-步行路径间的刚柔耦合模型,分析路径参数对机器人步态参数的影响规律。首先,采用基于自然零力矩点(ZMP)轨迹的步态规划方法,通过给定参考ZMP轨迹获取机器人质心轨迹,插值得到机器人在刚性路径下的步态;其次,基于Pasternak地基模型,在ANSYS中建立公路的多层柔性模型,导入ADAMS中与机器人多刚体模型耦合。通过3组柔性参数与理想刚性路面假设下的步行仿真,分析地面的柔性参数对机器人质心与ZMP轨迹、关节驱动力矩等参数的影响。研究结果表明:机器人在柔性地基公路上步行时质心高度比较稳定,波动小于2.6%,质心沿前进方向移动距离接近预期规划的步行距离,比刚性路径假设下的步行效率高;驱动力矩变化趋势与刚性路径变化趋势基本一致,其中支撑腿相应关节的驱动力矩突变峰值减少8.3%~33.4%,关节运动更平稳;足底接触力较刚性路径波动范围增大7.2%~16.7%,地面对机器人的冲击减少约8.0%。在自然柔性地面环境中,双足步行机器人的步态效率更高,运动更平稳。


