闪锌矿结构AlSb的嵌脱锂机理
颜 剑, 苏玉长, 苏继桃, 卢普涛
(中南大学 材料科学与工程学院, 长沙 410083)
摘 要:
利用第一原理赝势平面波计算方法研究具有闪锌矿结构AlSb的嵌脱锂机理。 通过计算不同嵌锂相Lix(AlSb)(0≤x≤2)或Li2+yAl1-ySb(0≤y≤1)的形成能(ΔE), 并结合相应的热力学原理便可得出当Li嵌入AlSb时的电压—比容量曲线图, 由此进一步确认了锂在嵌入AlSb的结构时, 首先是占据AlSb中的间隙位置, 然后随着Li嵌入量的增加, 可以逐步取代AlSb中的Al位置从而形成Li3Sb相。 通过分析Li嵌入AlSb前后的能带结构及态密度图可以发现, AlSb的导电性能首先随Li嵌入量的增加而增加, 当Li占据AlSb全部间隙位置后达到峰值, 当Li进一步替代Al时导电性能随之降低。
关键词: AlSb; 闪锌矿结构; 第一原理; 赝势平面波; 锂离子电池 中图分类号: TG146.2
文献标识码: A
Lithiation/delithiation mechanism of AlSb with zinc-blende structure
YAN Jian, SU Yu-chang, SU Ji-tao, LU Pu-tao
(School of Materials Science and Engineering,Central South University, Changsha 410083, China)
Abstract: The lithiation/delithiation mechanism of AlSb with zinc-blende structure was investigated by the first-principles pseudopotential plane wave method. The plot of potential vs specific capacity of Li intercalated into AlSb can be drawn by calculating the formation energies(ΔE) of different types of lithiated phases of Lix(AlSb)(0≤x≤2) or Li2+yAl1-ySb(0≤y≤1) in combination with the corresponding thermodynamic principles. It is found that Li first occupies the interstitial sites when intercalated into AlSb, and followed by substituting for Al sites with the increase of Li intercalation capacity to form the phase of Li3Sb. Through analyzing the band structure and the density of states of AlSb before and after lithiation, it is shown that the conductibility of AlSb increases with the increase of Li intercalation capacity, and reaches the peak value when Li occupies all the interstitial sites of AlSb, followed by decreasing when Li begins to substitute for Al.
Key words: AlSb; zinc-blende structure; first-principles; pseudopotential plane wave; lithium-ion batteries
锂离子电池作为一种全新的绿色化学充电电池, 具有比能量高、 电池电压高、 工作温度范围宽、 贮存寿命长等优点, 因而受到了众多研究者和商家的青睐[1]。 目前国内外已商业化生产的锂离子电池负极材料主要局限于各种类型的碳材料, 如天然石墨、 CN热解碳、 AN热解碳等。 不过由于这些碳材料存在着比容量低、 首次充放电效率低、 有机溶剂共嵌入等不足[2], 因而人们迫切需要寻找一种性能更好的非碳负极材料。 自1997年Idota等[3]报道了一种新型的具有高比容量和良好循环性能的非晶复合锡基氧化物负极材料(TCO)后, 锡基负极材料曾一度受到广大研究者的关注。 这是由于Sn能与Li形成含锂量非常高的Li22Sn5金属间化合物, 即平均1mol的Sn能容纳4.4mol的Li, 其相应的理论质量比容量为790mA·h/g, 是石墨理论比容量(372mA·h/g)的2倍多。 由Al-Li二元相图[4]可知, Al和Li可以形成3种稳定的金属间化合物: LiAl、 Li3Al2和Li9Al4。 因此, 铝也是有希望作为锂离子电池负极材料的, 而且其嵌锂容量也是比较高的, 最高可以达到平均1mol的Al容纳2.25mol的Li。 虽然铝没有锡那样高的嵌锂容量, 但是考虑到铝的相对原子质量(26.98)远远小于锡的相对原子质量(118.69), 所以铝负极的理论质量比容量(2234mA·h/g)是远远超过锡负极的。 即使当锂嵌入铝负极形成LiAl相时, 铝负极的质量比容量也高达993mA·h/g, 比锡负极的最大理论质量比容量还高, 所以, 铝基材料是一种很有发展前景的负极材料。
Hamon等[5]利用热蒸发沉积法制备了0.1μm到1μm间的铝薄片, 通过电化学测量发现这些铝薄片的质量比容量高达1000mA·h/g以上, 但由于其嵌锂相与脱锂相间的巨大体积差异, 使得它们的循环性能还远未达到实用化的要求。 因此Hamon等建议需在铝负极中添入第二相基体元素以形成金属间化合物或复合物材料, 将可大大提升铝基负极材料的循环性能, 这已得到Jeong等[6]和Lindsay等[7]的证实。 实际上, 在纯金属负极中添入第二相基体元素以形成金属间化合物或复合物材料能够显著地提升锂离子电池的循环性能不仅适用于铝基负极材料, 对其它的金属基负极材料也是适用的, 如NiSb2的循环性能就比纯Sb的循环性能好[8]。
第一原理计算方法相比纯粹实验有较大的优势, 它不需要进行大量的重复性实验, 只需要知道组成多粒子系统的原子序数和晶体结构参数, 就可以预知该系统的多种物理性能, 如平衡点阵常数、 结合能、 导电性能及相的相对稳定性等。 Ceder及其合作者们[9-11]曾利用第一原理系统地研究了锂离子电池用正极材料-锂过渡族金属氧化物的嵌脱锂性质, 得出了与实验结果非常吻合的理论预测。 但到目前为此, 有关负极材料的这方面的研究却比较少见。 为此本文作者拟采用第一原理赝势平面波方法研究锂离子电池用具有闪锌矿结构的AlSb负极材料的嵌脱锂机理。
1 第一原理方法的理论背景
第一原理是指在波恩-奥本海默(Born-Oppenheimer)近似和哈特里-福克(Hartree-Fock)近似的基础上, 在计算中仅仅使用普朗克常数h、 电子质量m和基本电荷e这3个基本物理常数, 以及原子的核外电子排布, 而不借助可调节的经验参数, 通过自洽计算来求解多粒子系统的薛定锷方程以得到系统的基态总能。

由于电子属于费米子(Fermions), 满足泡利不相容原理(Pauli exclusion principle)和费米-狄拉克统计(Fermi-Dirac Statistics), 所以式(1)中的近似程度过大, 忽略了电子之间的交换-相关效应, 使得计算的精度受到了一定的限制。 为了解决此问题, Hohenberg和Kohn于1964年提出了著名的密度泛函理论[12](Density Functional Theory, DFT)。 其基本想法是认为原子、 分子和固体的基态物理性质可以用电子密度函数n(r)来描述, 也就是可以归结为下面的两个基本定理。
定理一: 不计自旋的全同费米子系统的基态能量是电子密度函数n(r)的唯一泛函。
定理二: 能量泛函E[n(r)]在电子数不变的条件下对正确的电子密度函数n(r)取极小值, 并等于系统的基态能量。
由此可见, DFT不但给出了将多电子问题简化为单电子问题的理论基础, 同时也成为计算分子和固体的电子结构及总能的有力工具。 在DFT提出后不久, Kohn和Sham(沈吕九)[13]便将这套理论具体化了, 得出了Kohn-Sham总能泛函方程

可由下式给出
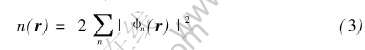
式中 因子2来源于电子的两个自旋方向。
只要知道电子间的相互交换-关联能泛函EXC[n(r)]的具体形式, 那么式(2)就可以通过自洽计算以得到多粒子系统的基态总能。 Kohn和Sham通过局域密度近似(Local Density Approximation, LDA)得到了EXC[n(r)]的一个近似表达式。 除LDA外, 广义梯度近似(Generalized Gradient Approximation, GGA)也被认为是一种非常好的EXC[n(r)]近似表达式, 尤其适用于计算物质的结合能[14]。
在实际应用中, 有多种手段可以实现第一原理的计算, 目前被广泛采用的是一种称为赝势平面波(Pseudopotential Plane Wave)的方法。 该方法的基本思想是将内层电子对孤立正电荷库仑势的屏蔽作用, 等价为一个在近原子核区域平缓变化的有效势, 并根据布洛赫定理(Bloch’s Theorem)将晶体中的单电子波函数用有限个平面波基函数展开。
2 计算软件及参数的选取
本研究采用的第一原理计算是通过由剑桥大学开发的Castep(Cambridge Sequential Total Energy Package)软件包[15]实现的。 电子间的相互交换-关联能泛函EXC[n(r)]采用GGA中的Perdew-Burke-Ernzerhof形式[14]。 选取倒易空间表征中的超软(ultrasoft)赝势[16]以取代原子核与内层电子对外层电子的作用势。 k值取点采用Monkhorst-Pack[17]方法选取6×6×6网格点。 平面波基函数的数目由动能截断点Ecut来决定, 即选取动能Ek=(h2/2m)|k+G|2不超过Ecut的平面波φk(r)=ck+Gexp[i(k+G)·r]作为展开晶体中单电子波函数的基函数。 经验证实选取Ecut=330.0eV已足够总能的收敛。 此外, 在计算每个多粒子系统晶胞的基态总能之前, 我们都用BFGS方法[18]对这些晶胞进行了几何优化, 以求得它们的局域最稳定结构。 自洽计算时, 体系总能量的收敛值取5.0×10-7 eV, 每个原子上的力要求低于0.1eV/nm, 公差偏移小于5.0×10-5 nm, 应力偏差小于0.02GPa。
3 计算结果及讨论
3.1 AlSb的结构与性能分析
在AlSb的闪锌矿结构中共有两种间隙位置供锂离子嵌入, 如下图1中所示。
由图1可见, 在AlSb结构中有大量适合锂离子嵌入的间隙位置, 而且当锂占据全部间隙位置后, 还可进一步取代其中的Al位置, 所以AlSb的嵌锂容量是非常可观的。
图2所示为AlSb的总能随晶格常数的变化曲线图。 令(dEtot/da)|a0=0, 可得AlSb的平衡晶格常数a0=0.6084nm, 与实验值aExp=0.6135nm比较吻合, 每个原胞对应的平衡总能为E0tot=-846.7364eV。
已知Al的原子半径和共价半径分别为raAl=0.1820nm和rcAl=0.1180nm; Sb的原子半径和共价半径分别为raSb=0.1530nm和rcSb=0.1400nm(半径数据取自软件CaRIne Crystallography 3.1)。 在AlSb中, 计算的相邻Al-Sb的原子间距为rAl-Sb=0.2631nm, 不难发现有
rcAl+rcSb〈rAl-Si〈raAl+raSb(4)
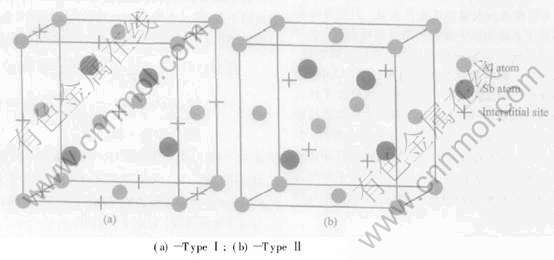
图1 闪锌矿结构AlSb中的两种间隙位置
Fig.1 Two types of interstitial sites in AlSb with zinc-blende structure
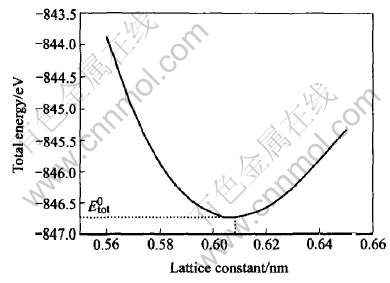
图2 AlSb总能随晶格常数的变化曲线
Fig.2 Curve of total energy of AlSb dependent on lattice constant
因此AlSb中, 各原子间的结合既有共价性部分又有金属性部分。
图3所示为AlSb原胞(含一个AlSb“分子”)的能带结构图和态密度图。 从能带结构图中可以看出AlSb的价带能级与导带能级未发生能带重叠, 其费米能级位于带隙内, 价带顶的能量为E+=0.005eV, 导带底的能量为E-=1.468eV, 其带隙宽度为Eg=E--E+=1.463eV, 由此可知AlSb应当是一种半导体材料。 从态密度图中可以看出在费米面附近的态密度值N(EF)=0.229eV非常小, 且主要由p态电子所贡献, 表明AlSb的金属性非常弱, 电子的共有化程度较低, 故其导电性能不是很好, 所以在将AlSb制成电极材料时, 应添加少量的导电剂以增加电极的导电能力。
3.2 AlSb的嵌脱锂性能分析
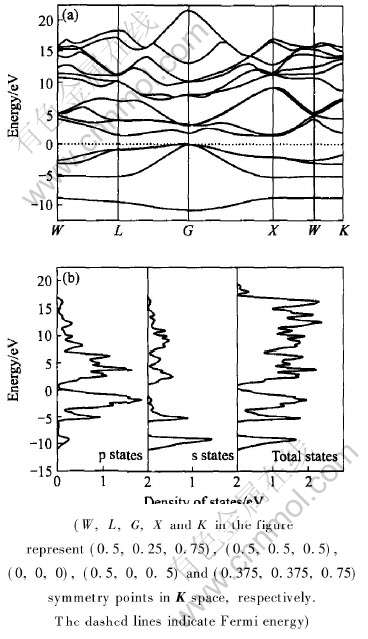
图3 AlSb原胞的(a)能带结构图和(b)态密度图
Fig.3 Band structure (a) and density of states (b) of AlSb primitive cell
假设Li在嵌入AlSb过程中并未改变AlSb的骨架结构, 首先嵌入占据到Type Ⅰ或Type Ⅱ两种间隙位置, 那么Li嵌入AlSb的电化学反应可表示为
![]()
由热力学原理可知, 反应(5)式的吉布斯自由能的变化ΔrG(x)与反应的平均电压μ(x)的关系为

又吉布斯自由能的变化ΔrG(x)可写为

由于通常情况下PΔV和TΔS项远远小于ΔE项, 故式(7)可近似表达为
![]()
而反应前后体系的总能之差ΔE又可表示为

联立式(6)、 (8)和(9)可得反应式(5)的平均电压值为

已知Li的总能为Etot(Li)=-190.0273eV, AlSb的总能Etot(AlSb)=-211.6690eV。 为计算Lix(AlSb)的总能, 可构造含4个Al原子和4个Sb原子的超胞, 即把一个含4个AlSb“分子”的晶胞看成一个固体物理学中的超胞, 然后再将Li逐渐填入超胞中的Type Ⅰ或Type Ⅱ间隙位置, 以得到形如Li(AlSb)4、 Li2(AlSb)4、 Li3(AlSb)4、 Li4(AlSb)4、 Li5(AlSb)4、 Li6(AlSb)4、 Li7(AlSb)4、 Li8(AlSb)4的超胞结构, 然后再计算这些超胞的总能(对于具有同一种分子式Liz(AlSb)4而含有几种不同Li占位情况的超胞, 则取其中总能的最小值)。 由此即可得Li1/4(AlSb)、 Li2/4(AlSb)、 Li3/4(AlSb)、 Li(AlSb)、 Li5/4(AlSb)、 Li6/4(AlSb)、 Li7/4(AlSb)、 Li2(AlSb)的总能, 然后再根据式(10)便可计算出形成Lix(AlSb)相的平均电压值, 如表1所示。
表1 Lix(AlSb)“分子”的总能及形成Lix(AlSb)相的平均电压值
Table 1 Total energies of Lix(AlSb) and average potentials for formations of Lix(AlSb) phases
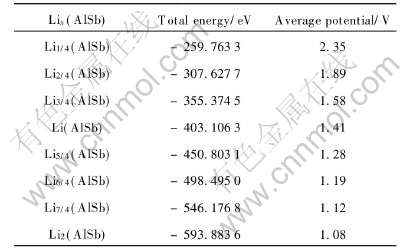
根据表1中的数据, 可以作出当Li占据AlSb中的间隙位置时的电压—嵌锂容量曲线图, 如图4所示。
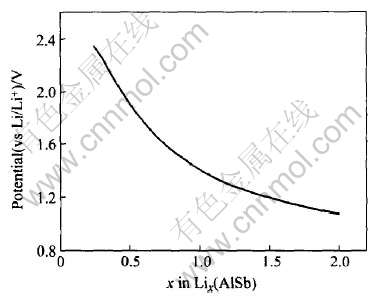
图4 Li占据AlSb中的间隙位置时的电压—容量曲线
Fig.4 Curve of potential vs Li intercalated capacity for Li occupying interstitial sites in AlSb
随Li嵌入量的增加, 当Li占据AlSb全部间隙位置后, Li可进一步取代AlSb结构中的Al原子位置以形成富锂相Li3Sb。 在此过程中, 假设Li取代Al后并不改变AlSb的晶体结构类型, 而只使得晶体的点阵常数发生少量的膨胀或缩小。 此时Li的嵌入反应可表为
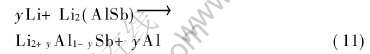
由上述同样的方法可得反应式(11)的平均电压值μ(x)为

已知Al的总能为Etot(Al)=-57.2059eV, Li的总能为Etot(Li)=-190.0273eV, Li2(AlSb)的总能为Etot[Li2(AlSb)]=-593.8836eV。 依前述方法共计算了4种不同y值(y=0.25, 0.50, 0.75, 1)的Li2+yAl1-ySb的总能, 再由式(12)便可计算出形成Li2+yAl1-ySb相的平均电压值, 如表2中所示。
表2 Li2+yAl1-ySb的总能及形成Li2+yAl1-ySb相的平均电压值
Table 2 Total energies of Li2+yAl1-ySb and average potentials for formations of Li2+yAl1-ySb phases

由表2中的数据, 可作出当Li取代Al后的电压—嵌锂容量曲线图, 如图5所示。
结合图4和图5中的数据, 并利用下式
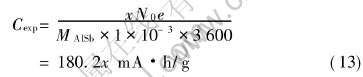
将Li的嵌入量换算成当Li嵌入AlSb电极时
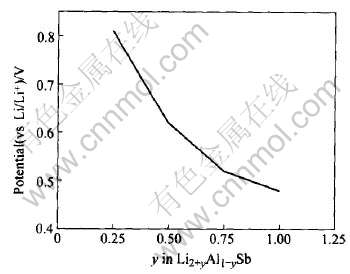
图5 Li取代Al后的电压—嵌锂容量曲线
Fig.5 Curve of potential vs Li intercalated capacity for Li substituting for Al
的质量比容量。 由此可作出当Li嵌入AlSb电极时电压—质量比容量曲线图, 如图6所示。 另外需要指出的是, 在式(12)中, x为嵌锂反应中的嵌锂个数, N0为阿伏加德罗常数, e为电子电量, MAlSb为AlSb的相对分子质量。
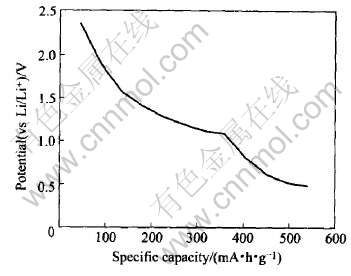
图6 Li嵌入AlSb电极时的电压—质量比容量曲线
Fig.6 Curve of potential vs specific capacity for Li intercalated into AlSb electrode
Honda等[19]曾用机械合金化的方法合成了AlSb的样品, 并对其进行了电化学性能的测量, 得到了恒电流充放电下的AlSb电极的电压—质量比容量曲线图, 将之与图6对比发现比较吻合, 从而证实了本文作者对AlSb材料的锂化反应机制的假设, 即Li在嵌入AlSb负极时, 首先占据的是其中的间隙位置, 随锂嵌入量的增加, 当占据完全部的间隙位置后, Li可以取代AlSb中的Al从而形成富锂相Li3Sb。
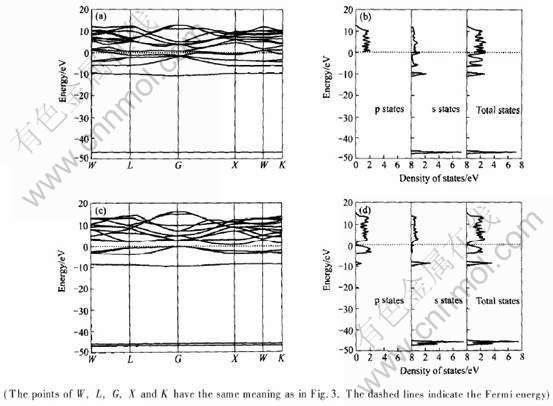
图7 Li2AlSb原胞的(a)能带结构图与(b)态密度图和Li3Sb原胞的(c)能带结构图与(d)态密度图
Fig.7 Band structure (a) and density of states (b) of primitive cell of Li2AlSb and band structure (c) and density of states (d) of primitive cell Li3Sb
图7给出了两种典型的嵌锂相Li2(AlSb)(取Lix(AlSb)中的x=2)和Li3Sb(取Li2+yAl1-ySb中的y=1)的能带结构图和态密度图。 在图7(a)中, 可以看到Li2(AlSb)的价带和导带在G点重合, 即带隙宽度Eg=0, 并且费米能级EF已移入导带中。 这表明当Li嵌入AlSb的间隙位置后形成的间隙固溶体是一种半金属, 其导电能力较原来的AlSb有所提高。 在图7(b)中, 可以看到Li2(AlSb)在费米面附近的态密度值N(EF)=2.124eV, 并且主要由s态和p态电子共同组成。 这表明在Li2(AlSb)中, 其电子共有化程度有所提高, 金属性也随之增强。 在图7(c)中, Li3Sb的价带和导带又重新分开, 其带隙宽度Eg=E--E+=0.753eV, 而费米能级EF又移入了带隙中。 这说明当Li占据全部间隙位置后, 因Li取代Al而形成的固溶体又变为半导体了, 其导电能力又有所降低。 在图7(d)中, 可以看出Li3Sb在费米面附近的态密度值N(EF)=0.265 eV。 这说明在Li3Sb中的电子共有化程度又有所下降, 其金属性也随之下降。 为了更清楚地说明AlSb的导电性能随Li嵌入量的增加的变化情况, 我们将各嵌锂相Lix(AlSb)(0≤x≤2)或Li2+yAl1-ySb(0≤y≤1)的带隙宽度Eg与其含锂量的变化情况作于图8中。 在图8中, 带隙宽度Eg越大的嵌锂相, 其导电性能越差; 反之, 带隙宽度Eg越小的嵌锂相, 其导电性能越好。
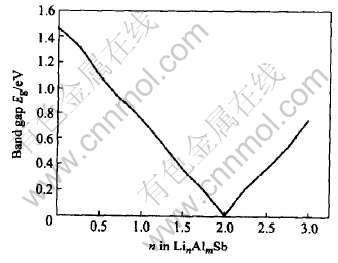
图8 嵌锂相LinAlmSb的带隙宽度Eg随其嵌锂量n的变化曲线
Fig.8 Curve of band gap Eg of lithiated phases LinAlmSb dependent on its lithiated capacity n
4 结论
由第一原理赝势平面波方法及有关的热力学原理得到了当Li嵌入AlSb电极时的理论电压—质量比容量曲线图, 并发现当Li在嵌入AlSb的晶体结构时, 首先占据的是其中的间隙位置, 然后随着锂嵌入量的增加, 当占据完全部间隙位置后, Li可以进一步取代AlSb中的Al从而形成富锂相Li3Sb。 通过分析Li嵌入AlSb前后的能带结构图和态密度图的变化, 发现AlSb的导电性能首先随Li嵌入量的增加而增加, 当Li占据AlSb所有间隙位置时达到峰值, Li进一步替代Al时导电性能则随之降低。
REFERENCES
[1]Tarascon J M, Armand M. Issues and challenges facing rechargeable lithium batteries[J]. Nature, 2001, 414: 359-367.
[2]Santos Pea J, Brousse T, Schleich D M. Search for suitable matrix for the use of tin-based anodes in lithium ion batteries[J]. Solid State Ionics, 2000, 135(1-4): 87-93.
[3]Idota Y, Kubota T, Matsufuji A, et al. Tin-based amorphous oxide: a high-capacity lithium-ion-storage material[J]. Science, 1997, 276: 1395-1397.
[4]Massalski T B, Murray J L, Bennett L H, et al. Binary Alloy Phase Diagrams[M]. Ohio: America Society for Metals, Metals Park, 1987.
[5]Hamon Y, Brousse T, Jousse F, et al. Aluminum negative electrode in lithium ion batteries[J]. J Power Sources, 2001, 97-98: 185-187.
[6]Jeong G J, Kim Y U, Sohn H J, et al. Particulate-reinforced Al-based composite material for anode in lithium secondary batteries[J]. J Power Sources, 2001, 101: 201-205.
[7]Lindsay M J, Wang G X, Liu H K. Al-based anode materials for Li-ion batteries[J]. J Power Sources, 2003, 119-121: 84-87.
[8]谢健, 赵新兵, 曹高劭, 等. 金属间化合物NiSb2吸放锂机理[J]. 中国有色金属学报, 2002, 12(6): 1238-1241.
XIE Jian, ZHAO Xin-bing, CAO Gao-shao, et al. Lithium absorption and release mechanism of intermetallic compound NiSb2[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(6): 1238-1241.
[9]Ceder G, Chiang Y M, Sadoway D R, et al. Identification of cathode materials for lithium batteries guided by first-principles calculations[J]. Nature, 1998, 392: 694-696.
[10]Aydinol M K, Kohan A F, Ceder G, et al. Ab initio study of lithium intercalation in metal oxides and metal dichalcogenides[J]. Phys Rev B, 1997, 56(3): 1354-1365.
[11]Ceder G, Aydinol M K, Kohan A F. Application of first-principles calculations to the design of rechargeable Li-batteries[J]. Comput Mater Sci, 1997, 8(1-2): 161-169.
[12]Hohenberg P, Kohn W. Inhomogeneous electron gas[J]. Phys Rev, 1964, 136(3B): B864-B871.
[13]Kohn W, Sham L J. Self-consistent equations including exchange and correlation effects[J]. Phys Rev, 1965, 140(4A): A1133-A1138.
[14]Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple[J]. Phys Rev Lett, 1996, 77(18): 3865-3868.
[15]Segall M D, Lindan P J D, Prober M J, et al. First-principles simulation: ideas, illustrations and the CASTEP code[J]. J Phys Condens Matter, 2002, 14: 2717-2744.
[16]Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J]. Phys Rev B, 1990, 41(11): 7892-7895.
[17]Monkhorst H J, Pack D. Special points for Brillouin-zone integrations[J]. Phys Rev B, 1976, 13(12): 5188-5192.
[18]Fischer T H, Almlof J. General methods for geometry and wavefunction optimization[J]. Journal of Physical Chemistry, 1992, 96: 9768-9774.
[19]Honda H, Sakaguchi H, Fukuda Y, et al. Anode behaviors of aluminum antimony synthesized by mechanical alloying for lithium secondary battery[J]. Mater Res Bull, 2003, 38(4): 647-656.
基金项目: 国家自然科学基金资助项目(50371103)
收稿日期: 2005-10-17; 修订日期: 2006-01-13
通讯作者: 苏玉长, 教授, 博士; 电话: 0731-8830785; 传真: 0731-8830785; E-mail: ycsu@mail.csu.edu.cn


