仿生射流表面优化设计与减阻机理分析

赵刚，李芳，杜军伟

(哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨，150001)

摘 要：

面参数减阻问题，建立仿生射流表面模型，利用SST k-ω湍流模型对其进行数值模拟，所得结果与实验数据吻合良好。运用正交试验设计法对影响射流表面摩擦阻力的因素进行分析，得到各因素对减阻效果和节能效果的影响规律：形状因子对减阻率和节能率的影响最大，流速比其次，流速比与减阻率和节能率呈抛物线关系，形状因子与减阻率呈线性关系，且随着形状因子增大减阻率增大，最大减阻率为15.06%，最大节能率为13.57%。由于射流流体的阻碍作用，在射流孔背流面形成逆流区，逆流区近壁面形成的剪应力方向与来流方向相反，局部摩擦因数为负值，并且由于射流流体对主流场的推力作用，使得边界层黏性底层厚度增大，速度梯度减小，摩擦阻力减小。

关键词：

射流表面；减阻；数值模拟；正交试验设计；边界层；

中图分类号：TB17             文献标志码：A         文章编号：1672-7207(2014)05-1449-08

Optimization design of bionic jet surface and mechanism analysis of drag reduction

ZHAO Gang, LI Fang, DU Junwei

(College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract: To solve the problem of the drag reduction on different jet surfaces, a bionic surface was built. The numerical simulation was completed by using the turbulence model of shear-stress transport SST k-ω. The result of the simulation is in conformity with the result of the experiment. The factors which affect the effect of the drag reduction on the jet surface were analyzed by using the orthogonal experimental .The results show that the effect of the shape factor on the drag reduction rate and the energy conservation rate is the best and the effect of the velocity ratio follows. The relationships between the velocity ratio and the drag reduction as well as the energy conservation are like a parabola. The relationship between the shape factor and the drag reduction rate is linear. The drag reduction rate increases with the increase of the shape factor, the drag reduction rate can reach the maximum of 15.06% and the energy conservation can reach the maximum of 13.57%. Because the fluid coming from the jet hole hinders the fluid on the surface, it will lead to a reverse flow region on the lee side of the jet hole. The direction of the shear stress near the wall of the reverse flow region is contrary to the direction of the fluid on the surface. The topical friction factor is negative. Because the fluid from the jet hole thrust the fluid on the surface, the thickness of the viscous sublayer of the boundary layer increases, the velocity gradient decreases, and the friction resistance decreases.

Key words: jet surface; drag reduction; numerical simulation; orthogonal experimental design; boundary layer

减阻提速、节能降耗是船舶研究设计人员的主要目标之一，研究发现，鲨鱼体表许多交错排列的沟槽结构能减小鲨鱼在水中游动的阻力。Walsh最先开展沟槽平板湍流减阻的研究^[1]，得出V型沟槽面具有最佳减阻效果的结论；王晋军等^[2]和宫武旗等^[3]分别对沟槽表面的减阻特性进行实验研究；陈莹等^[4]在旋成体模型表面粘贴铝基沟槽蒙皮，研究沟槽表面对模型阻力的影响，并给出基于来流单位雷诺数的沟槽尺寸无量纲公式；封贝贝等^[5]以壁面阻力系数为目标，对沟槽形貌构型进行优化，得到亚音速飞行时具有最佳减阻效果的壁面沟槽形貌构型参数；胡海豹等^[6]采用数值模拟方法获得脊状结构内部及附近流速、压强和涡量等细微流场结构的分布规律；Lazos等^[7]在物体表面上开横向或流向沟槽，通过实验发现横向沟槽不能减阻，沟槽应尽可能与流线方向一致^[8]；齐迎春等^[9]通过显示动力学接触分析，证明凹槽形针头具有减阻效果；任露泉等^[10-12]通过数值模拟和风洞试验等多种方法研究了亚音速、跨音速、超音速下凹坑、棱纹及凹环表面对旋成体阻力的影响。以上减阻方法都是通过改变边界层底层的流动结构来达到减阻的目的。Lucey等^[13]从理论上证明Kramer柔顺壁具有延迟转捩的作用；Kulik等^[14]研究表明柔顺壁能有效降低表面摩阻和流动噪声，降幅可达到17%；张庆利等^[15]进行用主动柔顺壁运动控制边界层转捩的实验研究，结果表明边界层转捩过程中的扰动即使已经发展到非线性阶段，也能被主动柔顺壁的运动所控制。柔顺壁减阻的优点是适用于任何运动状态。本项目组利用仿真、转化试验等方法^[16-19]验证了仿生射流表面具有减阻效果。本文建立了最接近鲨鱼鳃裂部位形状的射流表面模型，对单孔垂直射流减阻效果具有显著影响的因素进行量纲一化处理，通过正交试验法获得各因素的最优组合，并对仿生射流减阻机理进行分析。

1  仿生射流表面模型

1.1  仿生射流表面模型参数

为减小重力对射流表面的影响，本文的射流孔呈水平布置，计算域如图1所示，其参数为：沿流向方向为L_x，沿射流表面的法线方向为L_y，垂直方向为L_z=L_y；射流孔中心位于坐标原点；入口断面距坐标原点为L₁=10 mm；射流孔距两侧壁等距离，沿垂直方向为N_z，沿流向方向为N_x，射流孔面积为A_j=N_x×N_z。

影响射流表面摩擦阻力的因素较多，本文暂不考虑射流角度的影响，取射流速度方向与主流场方向垂直，即射流角度为90°；主流场速度v₁为10 m/s；射流速度v₂分别取为1，2和3 m/s，具体的模型参数如表2所示。为便于比较射流表面与光滑表面边界层流动特性，将计算流域的后表面作为与射流表面进行对照的光滑表面，二者具有相同的流场条件。

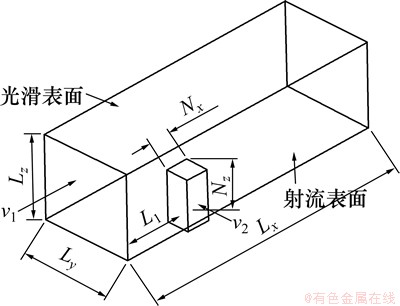
图1  计算域示意图

Fig. 1  Schematic of calculated regional

1.2  量纲分析

影响单孔垂直射流表面摩擦阻力F_j的主要因素为主流场速度v₁、射流速度v₂、射流孔沿流向方向N_x，射流孔沿垂向方向N_z，射流表面流向长度L_x，射流表面垂向长度L_z和流体密度ρ，选取仿生射流表面的摩擦阻力F_j为因变量，其余因素为自变量，其中选取v₁，ρ和N_x作为基本物理量，则有

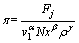
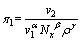
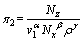
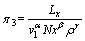
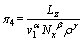
根据量纲和谐原理对π，π₁，π₂，π₃和π₄的待定系数求解，可得：

，，，，

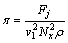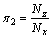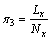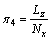
相似准数方程可写成

即

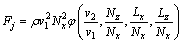
将射流速度与主流场速度的比值定义为流速比：

将射流孔形状因子定义为

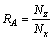
1.3  试验因素及水平的确定

影响仿生射流表面摩擦阻力的因素较多，为寻求能够取得较高减阻率和节能率的仿生射流表面参数，本文运用正交试验设计的方法进行研究，正交试验设计是研究多因素多水平的一种设计方法。

试验因素选择：A为流速比，B为形状因子，C为射流表面沿流向长度与射流孔沿流向长度的比值，D为射流表面沿垂向的长度与射流孔沿流向长度的比值；每个因素取3个水平，选用L₉(3⁴)正交表。

流速比取值范围为0.1~0.3，由于多数船舶的航行速度在20 kn左右，所以，取主流场速度为10 m/s。研究发现，射流速度越大减阻效果越好，但当射流速度大于3 m/s时，节能效果不明显，因此，射流速度分别取为1，2和3 m/s。本文的仿生对象为白斑星鲨，鳃裂长度均值为15 mm，宽度均值为3 mm。为节省计算资源，将射流孔参数缩小3倍，射流孔长度取为4~8 mm，宽度为1 mm。

2  数值模拟及计算方法验证

2.1  控制方程和湍流模型

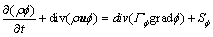
式中：ρ为流体密度；t为时间；u为速度矢量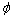；为通用因变量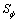；为广义源项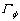；为广义扩散系数。表1所示为式(10)与连续方程、动量方程以及能量方程的对应关系，u_i为x，y和z方向的速度分量，μ为动力黏度。

表1  控制方程中各符号的具体形式

Table 1  Concrete terms of symbols in governing equation

湍流模型选用SST k-ω模型。SST k-ω模型由Menter发展而来，以便其在广泛的领域中可以独立于k-ε模型，并且在近壁自由流中k-ω模型有广泛的应用范围和精度。为此，将k-ε模型修改成k-ω模型。在不考虑浮力的情况下，k及ω运输方程如式(2)及式(3)所示，相关参数详见文献[18]。

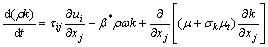
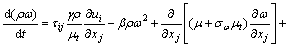
2.2  网格划分及边界条件

运用ICEM CFD14.0对计算域进行结构化网格划分，全局最大网格长度设置为0.4 mm，射流孔网格长度为0.2 mm，壁面第1层网格长度为0.002 mm，计算公式见式(13)，网格增长率为1.1，9个模型的网格单元数为(31.7~45.9)万，网格划分情况如图2所示。

式中：L_x为模型长度；v₁为主流场速度；△y⁺为第1层网格到壁面的无量纲距离。SST k-ω模型中要求△y⁺＜5，本文中取为1。

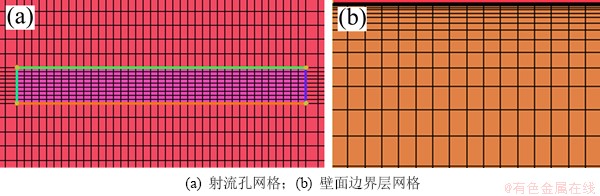
图2  仿生射流表面射流孔区域及壁面区域边界层网格

Fig. 2  Jet aperture meshes and boundary layer meshes of wall area for bionic jet surface

边界条件设置：入口断面主流场速度v₁=10 m/s，湍流强度为5%；出口为自由流；光滑表面、射流表面及射流孔壁面为无滑移绝热壁面；上、下断面为对称壁面；射流入口速度分别为1，2和3 m/s；数值计算中方程残差均设为1×10^-4。

2.3  数值检验

按照本文的数值模拟方法对文献[20]中的单孔水平射流进行仿真分析，射流孔直径为D，射流口位于x/D=0处，垂线位置分别在x/D=-2.44，0.18，2.81，5.43，8.05，10.02，12.64，15.27，17.89和20.51处。当流速比为6时，无量纲x方向上的平均流速在射流中心平面上的沿程变化如图3所示(其中，v₂为射流速度，v₁为主流场速度)。图3(a)为文献[20]中的实验结果，图3(b)为本文的仿真结果。分析图3可知：在近壁面处速度有差别，原因是试验中的射流表面为光滑表面，而本文要考虑射流表面的摩擦阻力，所以，本文选定的非光滑射流表面产生了摩擦阻力所致；在x/D=0.18垂线上有所不同，原因是实验中的射流口伸入流体区域，高出射流表面，而本文的射流口位于射流表面上，使得实验结果射流高度较大；其余部分的x方向流速变化几乎相同，间接证明了本文数值模拟结果的有效性。

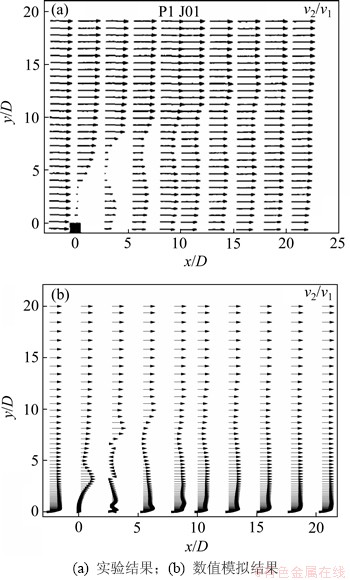
图3  y=0时，x方向流速v₂/v₁沿程分布

Fig. 3  Distribution along path of x-velocity v₂/v₁ when y=0

3  结果与分析

3.1  减阻及节能效果评价

仿生射流表面减阻率计算式为

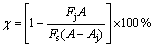
式中：χ为减阻率；F_s为光滑表面所受阻力；F_j为射流表面所受阻力；A为光滑表面面积；A_j为射流孔面积。

模型表面所受阻力包括黏性阻力和压差阻力2部分，由于本文中射流方向与主流场速度方向垂直，光滑表面的压差阻力为0，射流表面的压差阻力量级为10^-17，可忽略不计，所以，本文只考虑黏性阻力对模型表面的影响。

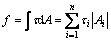
式中：f为黏性阻力；τ为壁面剪应力；A为壁面面积；τ_i为壁面离散单元剪应力；A_i为壁面离散单元面积。

仿生射流表面减阻系统总能耗为

对照表面总能耗为

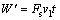
仿生射流表面节能率计算式为

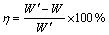
将式(14)，(16)和(17)带入到式(18)化简后得

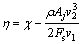
式中：v₁为主流场速度；v₂为射流速度；t为时间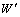；为对照表面总能耗；η为节能率；ρ为流体介质的密度。

3.2  正交试验设计结果及分析

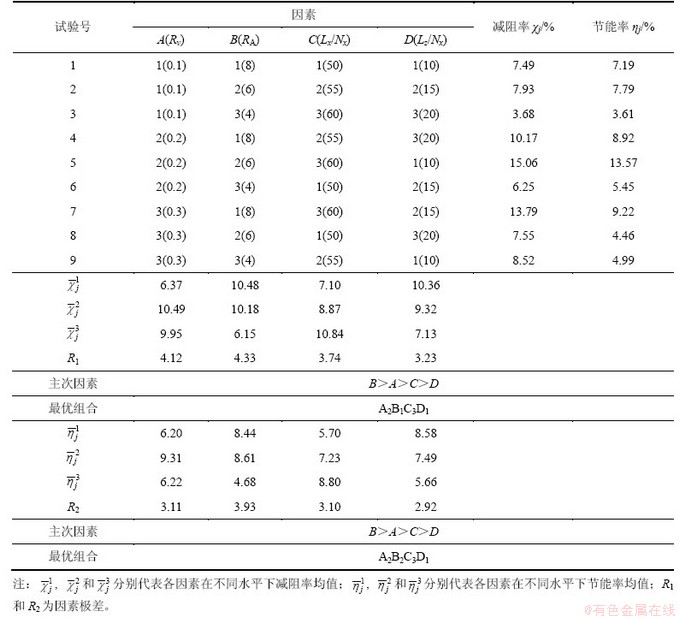
试验方案选择及结果分析见表2。图4所示为各因素不同水平均值对减阻率和节能率的影响规律。由极差分析可知：形状因子R_A对减阻率和节能率的影响最大，当其他因素固定不变时，减阻率与形状因子呈线性递增关系，节能率与形状因子呈抛物线关系；当R_A=6时，节能率最大；流速比对减阻率和节能率的影响其次，当其他因素固定不变时，减阻率和节能率与流速比呈抛物线关系，当流速比为0.2时，减阻率和节能率最大；射流表面沿垂向宽度与射流孔沿流向长度比值L_z/N_x对减阻率和节能率影响最小，当其他因素不变时，减阻率和节能率与其呈线性关系；随着L_z/N_x的增大，减阻率和节能率逐渐减小；射流表面沿流向的长度与射流孔沿流向长度的比值L_x/N_x对减阻率和节能率的影响仅比L_z/N_x的影响大，当其他因素不变时，减阻率和节能率与L_x/N_x呈线性关系，随着L_x/N_x的增大，减阻率和节能率增大。

表2  试验方案及结果分析

Table 2  Experiment plan and analysis of result

3.3  减阻原因分析

光滑表面和仿生射流表面所受的摩擦阻力包括黏性剪切应力和湍流雷诺应力，其表达式为

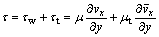
式中：μ为流体黏性系数；μ_t为湍流黏性系数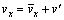；，即瞬时速度v_x是时均速度与脉动速度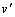的叠加。仿生射流表面主要通过减小黏性剪应力来减小摩擦阻力。

图5所示为第5号试验模型在流速比为0.1，0.2和0.3时的射流中心对称面上x方向速度对比云图，分析图5可知：流速比越大，射流流体的射入深度越大，逆流区长度越大，边界层底层负剪应力区的范围越大，逆流区的存在对减小壁面的摩擦阻力具有显著的效果。但是流速比越大，射流表面附近的湍流强度越大，消耗的湍动能越大，如图6所示。图6所示为与图5对应的湍流强度和湍动能对比云图。从雷诺应力的成因可知：当主流场速度不变时，随着射流速度的增大，雷诺应力增大。黏性剪应力和雷诺应力是减阻率与流速比呈抛物线关系的主要因素。

由极差分析可知：形状因子对减阻率影响最大，原因是射流流体对主流流体的阻挡，主流场绕流射流流体形成反向旋转涡对，射流厚度(即射流流体沿垂向高度)的变化与流速比无关，只是y/N_z的函数：

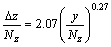
式中：△z为射流厚度；N_z为射流孔沿垂向的高度。

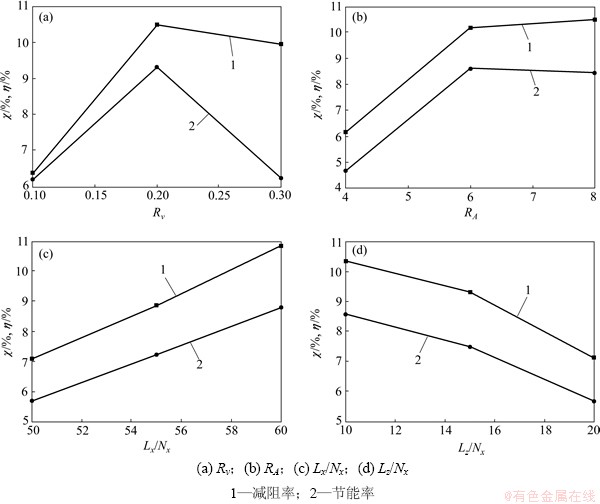
图4  各因素水平对减阻率和节能率影响规律

Fig. 4  Influence rules of levels of various factors on drag reduction rate and energy saving rate

图5  z=0，不同流速比时的流向速度对比云图

Fig. 5  Comparison of x-velocity with different velocities ratios at z=0

射流厚度越大，边界层底层厚度大的区域越大，减阻效果越好。图7所示为1，5和9号试验模型在x/N_x=2处的速度对比云图，分析图7可知：N_z越大，射流厚度越大。

综上，射流减阻原因有2点：(1) 由于射流对来流的阻挡在射流孔迎流面形成马蹄形漩涡，在射流孔背流面形成负压区，因此，在射流孔迎流面和背流面均形成逆流区，逆流区边界层底层的速度方向与主流场方向相反，形成负的剪应力，具有明显的减阻效果；(2) 在射流孔下游形成反向旋转涡对，射流流体给反向涡提供了足够的能量，使得反向涡不断向下游延伸，并在壁面处诱导出二次涡，使边界层黏性底层厚度增大，近壁面的速度梯度减小，摩擦阻力减小。

图6  z=0，不同流速比时的湍流强度和湍动能对比云图

Fig. 6  Comparison of turbulence intensities and turbulent kinetic energies with different velocities ratios at z=0

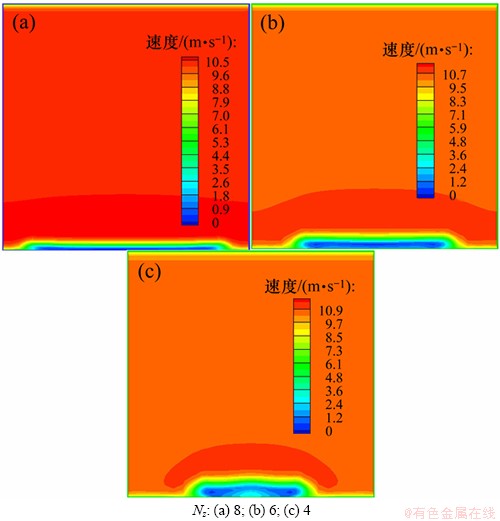
图7  x/N_x=2，N_z不同时的速度对比云图

Fig. 7  Comparison of velocities with different value of N_z at x/N_x=2

4  结论

(1) 仿生射流表面具有较好的减阻和节能效果，最高减阻率为15.06%，最大节能率为13.57%。

(2) 4个射流表面模型参数均具有减阻和节能效果，其中形状因子对减阻率和节能率影响最大，流速比其次，L_x/N_x再次，L_z/N_x最小；流速比与减阻率和节能率呈抛物线关系，形状因子与减阻率呈线性关系，随着形状因子的增大，减阻率增大，节能率先增大后减小。

(3) 由于射流流体的阻碍作用，在射流孔背流面形成逆流区，逆流区内近壁面的速度方向与来流方向相反，局部摩擦因数为负值，对减阻效果影响显著；而且在射流孔下游形成反向旋转涡对并不断向下游延伸，在壁面处诱导出二次涡，使得边界层黏性底层的厚度增大，速度梯度减小，起到了减阻效果。

参考文献：

[1] Walsh M J. Riblets as a viscous drag reduction technique[J]. AIAA Journal, 1983, 21(4): 485-486.

[2] 王晋军, 兰世隆, 陈光. 沟槽面湍流边界层结构实验研究[J]. 力学学报, 2000, 32(5): 621-626.

WANG Jinjun, LAN Shilong, CHEN Guang. Experimental study on the turbulent boundary layer flow over riblets surface[J]. Acta Mechanica Sinica, 2000, 32(5): 621-626.

[3] 宫武旗, 李新宏, 黄淑娟. 沟槽壁面减阻机理实验研究[J]. 工程热物理学报, 2002, 23(5): 579-582.

GONG Wuqi, LI Xinhong, HUANG Shujuan. Experiment study on the mechanism of riblets drag reduction[J]. Journal of Engineering Thermophysics, 2002, 23(5): 579-582.

[4] 陈莹, 陈迎春, 黄炜, 等. 旋成体表面沟槽减阻试验研究[J]. 实验流体力学, 2012, 26(2): 42-45.

CHEN Ying, CHEN Yingchun, HUANG Wei, et al. Experiment investigation of drag reduction using reblets for a slender body[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(2): 42-45.

[5] 封贝贝, 陈大融, 汪家道. 亚音速飞行器壁面沟槽减阻研究与应用[J]. 清华大学学报(自然科学版), 2012, 52(7): 967-972.

FENG Beibei, CHEN Darong, WANG Jiadao. Riblet surface drag reduction on subsonic aircraft[J]. Journal of Tsinghua University (Science and Technology), 2012, 52(7): 967-972.

[6] 胡海豹, 宋保维, 刘占一, 等. 脊状表面流场数值计算方法研究[J]. 空气动力学学报, 2011, 29(3): 348-354.

HU Haibao, SONG Baowei, LIU Zhanyi, et al. Research at the computational methods of flow fields over riblets surface[J]. Acta Aerodynamica Sinica, 2011, 29(3): 348-354.

[7] Lazos B S, Wilkinson S P. Turbulent viscous drag reduction with thin element riblets[J]. AIAA Journal, 1988, 26(4): 496-498.

[8] Walsh M J, Sellers W L, Mcginley C B. Riblet drag at flight conditions[J]. Journal of Aircraft, 1989, 26(6): 570-575.

[9] 齐迎春, 丛茜, 王骥月, 等. 凹槽形仿生针头优化设计与减阻机理分析[J]. 机械工程学报, 2012, 48(15): 126-130.

QI Yingchun, CONG Qian, WANG Jiyue, et al. Optimization design and drag reduction mechanism research on groove shape bionic needle[J]. Journal of Mechanical Engineering, 2012, 48(15): 126-130.

[10] 任露泉, 张成春, 田丽梅. 仿生非光滑用于旋成体减阻的试验研究[J]. 吉林大学学报(工学版), 2005, 35(4): 431-436.

REN Luquan, ZHANG Chengchun, TIAN Limei. Experimental study on drag reduction for bodies of revolution using bionic non-smoothness[J]. Journal of Jilin University of Technology (Natural Science Edition), 2005, 35(4): 431-436.

[11] 张成春, 任露泉, 王晶. 旋成体仿生凹坑表面减阻的试验分析及数值模拟[J]. 吉林大学学报(工学版), 2007, 37(1): 100-105.

ZHANG Chengchun, REN Luquan, WANG Jing. Experiment and numerical simulation on drag reduction for bodies of revolution using bionic scrobiculate ringed surface[J]. Journal of Jilin University of Technology (Natural Science Edition), 2007, 37(1): 100-105.

[12] 张成春, 任露泉, 刘庆平, 等. 旋成体仿生凹坑表面减阻试验研究[J]. 空气动力学学报, 2008, 26(1): 79-84.

ZHANG Chengchun, REN Luquan, LIU Qingping, et al. Experimental study on bionic dimpled surface of bodies of revolution for drag reduction[J]. Acta Aerodynamica Sinica, 2008, 26(1): 79-84.

[13] Lucey A D, Carpenter P W. A numerical simulation of the interaction of a compliant wall and inviscid flow[J]. Fluid Mechanics, 1992, 234: 121-146.

[14] Kulik V M, Semenov B N. The measurement of dynamic properties of viscose plastic aterials for turbulent drag reduction[J]. Emerging Techniques in Drag Reduction Mechanical Engineering Publications London, 1996, 432: 207-216.

[15] 张庆利, 李京伯. 用主动柔顺壁运动控制边界层转捩[J]. 空气动力学学报, 1999, 17(3): 333-337.

ZHANG Qingli, LI Jingbo. Control of boundary layer transition using active compliant wall motion[J]. Acta Aerodynamica Sinica, 1999, 17(3): 333-337.

[16] 赵刚, 谷云庆, 许国玉, 等. 仿生射流表面减阻特性实验研究[J]. 中南大学学报(自然科学版), 2012, 43(8): 3007-3012.

ZHAO Gang, GU Yunqing, XU Guoyu, et al. Experimental study on drag reduction characteristics of bionic jet surface[J]. Journal of Central South University (Science and Technology), 2012, 43(8): 3007-3012.

[17] 谷云庆, 赵刚, 赵华琳, 等. 仿鲨鱼鳃部射流减阻特性的仿真研究[J]. 兵工学报, 2012, 33(10): 1230-1236.

GU Yunqing, ZHAO Gang, ZHAO Hualin, et al. Simulation study on drag reduction characteristics of bionic jet flow based on shark gill[J]. Acta Armamentarii, 2012, 33(10): 1230-1236.

[18] 谷云庆, 赵刚, 郑金兴, 等. 射流表面的射流角度与射流速度耦合减阻特性[J]. 西安交通大学学报, 2012, 46(9): 71-77.

GU Yunqing, ZHAO Gang, ZHENG Jinxing, et al. Drag reduction characteristics on jetting surface with jet angle-jet velocity coupling[J]. Journal of Xi’an Jiaotong University, 2012, 46(9): 71-77.

[19] 谷云庆, 赵刚, 郑金兴, 等. 射流表面主流场速度与射流速度耦合减阻特性[J]. 中南大学学报(自然科学版), 2012, 43(12): 4713-4721.

GU Yunqing, ZHAO Gang, ZHENG Jinxing, et al. Characteristics of drag reduction on coupling of jet surface main flow field velocity and jet velocity[J]. Journal of Central South University (Science and Technology), 2012, 43(12): 4713-4721.

[20] 肖洋. 横向流动条件下多孔水平动量射流掺混特性研究[D]. 南京: 河海大学水利水电工程学院, 2005: 49-50.

XIAO Yang. The study on mixing characteristics of a tandem multiple jet group in cross-flow[D]. Nanjing: Hohai University. College of Water Conservancy and Hydropower Engineering, 2005: 49-50.

(编辑  何运斌)

收稿日期：2013-06-08；修回日期：2013-08-06

基金项目：国家自然科学基金资助项目(51275102)

通信作者：李芳(1985-)，女，黑龙江绥化人，博士研究生，从事仿生射流减阻技术研究；电话：18745136760；E-mail: lifang71118@163.com

摘要：针对不同射流表面参数减阻问题，建立仿生射流表面模型，利用SST k-ω湍流模型对其进行数值模拟，所得结果与实验数据吻合良好。运用正交试验设计法对影响射流表面摩擦阻力的因素进行分析，得到各因素对减阻效果和节能效果的影响规律：形状因子对减阻率和节能率的影响最大，流速比其次，流速比与减阻率和节能率呈抛物线关系，形状因子与减阻率呈线性关系，且随着形状因子增大减阻率增大，最大减阻率为15.06%，最大节能率为13.57%。由于射流流体的阻碍作用，在射流孔背流面形成逆流区，逆流区近壁面形成的剪应力方向与来流方向相反，局部摩擦因数为负值，并且由于射流流体对主流场的推力作用，使得边界层黏性底层厚度增大，速度梯度减小，摩擦阻力减小。