Trans. Nonferrous Met. Soc. China 24(2014) 1500-1505
A first-principles study on interfacial properties of Ni(001)/Ni3Nb(001)
Zhi-qin WEN1, Yu-hong ZHAO1, Hua HOU1, Nan WANG1, Li FU1, Pei-de HAN2
1. College of Materials Science and Engineering, North University of China, Taiyuan 030051, China;
2. College of Materials Science and Engineering, Taiyuan University of Technology, Taiyuan 030024, China
Received 8 May 2013; accepted 19 October 2013
Abstract:
The Ni (001) surface, Ni3Nb (001) surface and Ni (001)/Ni3Nb (001) interfaces were studied using the first-principles pseudopotential plane-wave method. The adhesion work, thermal stability and electronic structure of Ni/Ni3Nb (001) interfaces were calculated to expound the influence of atom termination and stacking sequence on the interface strength and stability. Simulated results indicate that Ni and Ni3Nb (001) surface models with more than eight atomic layers exhibit bulk-like interior. The (Ni+Nb)-terminated interface with hollow site stacking has the largest cohesive strength and critical stress for crack propagation and the best thermal stability among the four models. This interfacial Ni and the first nearest neighbor Nb atoms form covalent bonds across the interface region, which are mainly contributed by Nb 4d and Ni 3d valence electrons. By comparison, the thermal stability of Ni/Ni3Nb (001) interfaces is worse than Ni/Ni3Al (001) interface, implying that the former is harder to form. But the Ni/Ni3Nb interface can improve the mechanical properties of Ni-based superalloys.
Key words:
Ni3Nb; first-principles; interface; electronic structure;
1 Introduction
Ni-based single-crystal (SC) superalloys, which mainly consist of a high volume fraction of γ′ phase precipitates coherently dispersed on a γ matrix, are widely used for turbine blades and vanes in the most advanced gas turbine engines because of their remarkable mechanical properties [1]. The γ′ precipitates (an intermetallic phase of stoichiometry based upon Ni3Al) possess a L12-type ordered face-centered cubic (FCC) structure. The γ matrix has a FCC structure. Inconel 718, 706 and 625 are dominant in the commercial superalloys, whose content of Nb is 3%-5.5%. γ′′-Ni3Nb phase precipitates significantly improve overall performance of the superalloys, especially the high-temperature creep rupture strength. To some extent, those unique high-temperature properties of superalloys mostly depend on the cohesive strength and the bonding characteristics of the γ-Ni/γ′′-Ni3Nb interfaces.
The γ′′-Ni3Nb phase is largely responsible for the elevated-temperature strength of Ni-based SC superalloys, and it exhibits a body-centered tetragonal (BCT) D022 crystal structure [2]. In order to realize the structural, mechanical and electronic properties of δ phase and γ′′ phase in Inconel 718 superalloy, DAI and LIU [3] made first-principles calculation, and found that δ phase is thermodynamically more stable than γ′′ phase and both phases are hard and have good ductility. ANNARUMMA and TURPIN [4] studied the structure and mechanical behavior of directionally solidified Ni/Ni3Nb eutectic interfaces, and their results indicated that when the temperature is lowered, supersaturation in the nickel-rich phase is relieved mostly by precipitation and the material exhibits high ductility at temperatures up to 600 °C if the structure is regular. Up to now, many experiments and theory simulation have been done to investigate the Ni/Ni3Al interfaces, proving that alloying elements at the Ni/Ni3Al interfaces have a great influence on the strength and ductility of the Ni-based SC superalloys [5-10]. However, few studies have been made to investigate the Ni/Ni3Nb interfaces. Hence, an in-depth and thorough understanding of their strengthening and stability mechanism of the Ni/Ni3Nb interfaces by calculating the cohesive manner, electronic structure, mechanical properties and thermal properties are necessary in order to guide the design of a new generation in Ni-based SC superalloys.
In this work, first-principles method was used to simulate the work of adhesion, thermal stability and electronic structure of γ/γ′′ phase (001) interfaces. A more reasonable supercell and a completely coherent γ/γ′′ interfaces ignoring the strain effect at the interface were used to simulate the real interfaces.
2 Model and methods
Figure 1 illustrates the stacking sequence of (001) Ni and (001) Ni3Nb surfaces. The hollow site model and the top site model were considered in our calculations for (001) γ/γ′′ interfaces. The hollow site indicates the Ni atom resides on the middle sites of Ni3Nb slabs, the top site indicates that the interfacial Ni atom is directly placed on-top the surface Ni or Nb atoms of Ni3Nb slabs. We modelled γ-Ni/γ′′-Ni3Nb interfaces system with a repeated slab construction with three-dimensional translational symmetry. The lattice constants of the Ni/Ni3Nb (001) systems, with a lattice mismatch of about 1.7%, were taken to be equal for γ′′-Ni3Nb bulk. The Ni (001) slab was stretched by 1.7% with the coherent interface approximation. The Ni/Ni3Nb (001) interfaces were assumed to be complete coherence. Hence, we ignored the strain effect at the interface. The atomic arrangements in the Ni/Ni3Nb (001) interfaces model are shown in Fig. 2.
Fig. 1 Ni surface orientated [001] direction with stacking sequence (ABABAB……) (a) and Ni3Nb surface orientated [001] direction with stacking sequence (ABCBABCBABCB……) (b)
Fig. 2 Atomic structure of γ/γ′′ (001) interfaces
Calculations of electronic structure and total energy were carried out using the Cambridge serial total energy package (CASTEP) within the framework of density functional theory (DFT) [11,12], a first-principles pseudopotential plane-wave method was used in this work. Ultrasoft pseudopotentials [13] represented in reciprocal space with an exchange-correction function of Perdew-Wang91 (PW91) form under generalized gradient approximation (GGA) [14] were applied for all the models. The cutoff energy of atomic wave functions (PWs), Ecut, was set at 500.0 eV, and the k points were set to be 8×8×8, 8×8×4, 8×8×2 and 8×8×1 for bulk Ni, Ni3Nb, (001) free surface and (001) interface models, respectively. All atoms were relaxed to their equilibrium positions to fulfill geometry optimization by Broyden- Fletcher-Goldfarb-Shanno (BFGS) scheme [15]. The convergence tolerance was set as energy of 2.0×10-5eV/atom, the maximum force of 0.05 eV/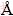 
, the maximum stress of 0.1 GPa, and the maximum displacement of 0.002 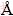. The valence electrons considered in their pseudopotential are Ni 3d8 4s2, Nb 4s2 4p6 4d4 5s1, respectively. Surface and interfaces were modeled using supercell approach in periodic boundary conditions and the thickness of vacuum layer was 10.0 .
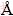3 Bulk and surface calculations
3.1 Bulk properties
The calculated lattice constants and bulk modulus for bulk Ni and Ni3Nb are listed in Table 1. It is found that the lattice parameters and bulk modulus of both two materials are in good accordance with other DFT calculated results and experiment results, which demonstrates the reliability of our approach.
Table 1 Lattice constants a0and bulk modulus BT
3.2 Surface convergence
The surface energy (γs) is one of the basic qualities to describe stabilities of surface, which is usually calculated according to the formula as below [19]:
(1)
where Eslab(N) is the total energy of surface supercell slab, N is the total number of atoms in the slab; Ebulk is the total energy per each atom in the bulk material; As is the corresponding surface area.
Both sides of the surface slab between Ni and Ni3Nb should be thick enough to ensure the bulk-like interior, and the calculation will be more accurate if the surface slab contains more atom layers, but on the other side, the computation will need more memory hardware and longer computing time, so it is reasonable to conduct convergence tests before deciding the atom layers.
Table 2 lists the convergence tests of the surface energy of Ni (001) and Ni3Nb (001), respectively. It is shown that the Ni (001) slabs converge well when the surface cell contains more than eight layers. Accordingly, the Ni slab geometry with eight atomic layers was adopted in the following calculations. There are two kinds of Ni3Nb (001) polar surfaces. Therefore, Ni- and (Ni+Nb)-terminated surfaces energies were calculated. It is revealed that the surface energy for the Ni-terminated surface is larger than that for the (Ni+Nb)-terminated surface, which implies that the (Ni+Nb)-terminated surface is more stable than the Ni-terminated surface. It is also found that Ni3Nb (001) surface energy converges well when the slab number is more than eight. Hence, eight atomic layers were adopted for Ni3Nb (001) slab geometry in the following calculations to ensure the bulk-like interior.
Table 2 Ni (001) and Ni3Nb (001) surface convergence tests of surface energy (γs) with respect to number of layers
4 Ni (001)/Ni3Nb (001) interfaces
4.1 Work of adhesion
Critical stress of crack propagating was calculated by the Griffith equation [20]:
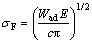(2)
where σF is the critical stress for crack propagation; E is the elastic modulus; c is the length of a surface crack. Thus, σF depends only on Wad. Adhesion work Wad is defined as reversible work needed to separate an interface into two slabs, which can be used to quantitatively predict the mechanical properties of the interface and determined by the following equation [8]:
(3)
where EA/B is the total energy of an A/B interface system; Eslab denotes the total energy of fully relaxed surface slabs; Ai is the interface area.
In this work, both hollow site models and top site models were calculated from the fully relaxed interface supercell. The values of adhesion work and interfacial separation are listed in Table 3. It is clear that (Ni+Nb)-terminated interface has larger adhesion work and smaller interfacial separation than Ni-terminated interfaces; the stacking sequence also has a direct influence on the adhesion work and interfacial separation, the adhesion work decreases as the order of hollow and top site interfaces, while the interfacial separation increases as the same order. The value of Wad for the (Ni+Nb)-terminated interface with hollow site stacking sequence is the largest, and its d0 is the smallest among the four models. Therefore, the two interfaces termination structures, the (Ni+Nb)-terminated interfaces yields are in stronger adhesion, and the hollow site stacking sequence is preferable to continue the natural stacking sequence of bulk Ni and Ni3Nb, which means that the (Ni+Nb)-terminated interface with hollow site model has the largest cohesive strength and critical stress for crack propagation among the four models. The value of Wad for the (001) interface of (Ni+Nb)-terminated layer bonding with hollow site stacking of Ni is 8.90 J/m2. WANG et al [8] using the same methodology as this work, which was performed by first-principles method based on DFT, calculated Wad of Ni/Ni3Al (001) interface (4.14 J/m2). This means that the precipitates of Ni3Nb in Ni-based single-crystal superalloys can improve the tensile strength yield and strength of alloy.
Table 3 Adhesion work (Wad) and interface separation (d0) obtained with four models
4.2 Thermal stability
Thermal stability of interface is usually described by λi, which is commonly expressed as [8]
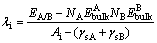(4)
where λi is used to predict cohesive strength of interface systems and can be viewed as the work required to create from bulk materials; N is the total number of bulk materials; γsA and γsB are the areas of bulk materials. λi denotes a standard expression for interfacial energy. The precipitation kinetics is influenced by the interfacial energy between the precipitate phase and the matrix phase. Therefore, it should be an important parameter in the formation of Ni3Nb in Ni metal during sintering in which the interface obtains their characteristic orientations.
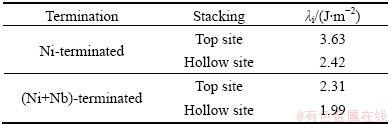
Table 4 lists λi values obtained from our calculation. It is clear that hollow site models have better thermal stability than top site models, and thermal stability of (Ni+Nb)-terminated interfaces is better than that for Ni-terminated interfaces. The (Ni+Nb)-terminated interface with hollow site stacking has the best thermal stability, which means that this structure is the most easily formed interface among the four models. WANG et al [8] using the same equation calculated the thermal stability of Ni/Ni3Al (001) interfaces by first-principles method, which is implemented in Vienna ab initio simulation package VASP. The λi value of Ni+Al-terminated interface with hollow site stacking is 0.12 J/m2, which is smaller than that of Ni/Ni3Nb (001) interfaces (1.99 J/m2). This means that the former is more stable than the later. Unfortunately, there is not any experimental data to compare with this result and it is necessary to be experimentally confirmed in the future works.
Table 4 λi value obtained from four models
4.3 Electronic structure
To reveal the nature of the interfacial bonding and the electronic structure of Ni/Ni3Nb (001) interfaces, the (Ni+Nb)-terminated interface with top site and hollow site stacking was analyzed. Figure 3 illustrates the partial and total electronic densities of states of two models from -10 eV to 2 eV. As shown in Fig. 3(a), the main bonding peaks of the (Ni+Nb)-terminated interface with top site stacking are between -9 eV and 2 eV, which is mainly contributed by Nb 4d and Ni 3d valence electrons. It is same to the hollow site stacking interface shown in Fig. 3(b). The valence electron numbers between -10 eV and the Fermi level of the top site and hollow site model are 9.2121 and 9.2574 eV/atom, respectively. The smaller the valence electron number is, the weaker the charge interactions are. Hence, the hollow site model makes a stronger hybrid than the top site model between Nb 4d and Ni 3d orbital atoms, indicating that the hollow site model is more stable than the others. So, it supports the above conclusion that the hollow site model has better mechanical properties.
Figure 4 plots the charge density difference on the cross-section of the two coherent interfacial layers of the Ni/Ni3Nb interfacial supercells with (Ni+Nb)- termination. This cross-section is (100) plane for all interfacial models. In Fig. 4(a), the charge accumulation is obvious for Ni atoms and the first nearest neighbor (FNN) Nb atoms on the cross-section of Ni/Ni3Nb interface, which is typically characteristic of a covalent bonding. It is also easy found that the FNN Ni-Nb atoms are mainly covalent bonding in the γ′′-Ni3Nb block, and the FNN Ni-Ni atoms are mainly metallic bonding in the γ-Ni block. For the top site model, the interfacial Ni atoms are dragged very near to the interfacial Nb atoms where the charge accumulation is obvious, to form covalent bonding features at the interface. In addition, it reveals that the FNN Ni-Nb atoms are mainly covalent bonding in the γ′′-Ni3Nb block, and the FNN Ni-Ni atoms are mainly metallic bonding in the γ-Ni block as shown in Fig. 4(b).
Fig. 3 Partial and total electronic density of states of Ni/Ni3Nb (001) interfaces with (Ni+Nb)-termination
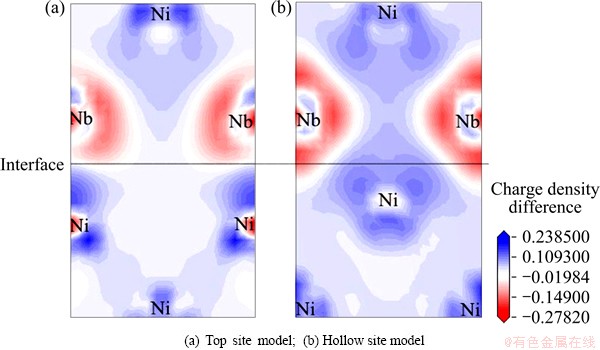
Fig. 4 Distribution of charge density difference of Ni/Ni3Nb (001) interfaces with (Ni+Nb)-termination along (100) plane
4.4 Population analysis
In order to qualitatively evaluate the electronic distribution and transfer of Ni/Ni3Nb (001) interfaces, we further calculated the Mulliken’s charge of the (Ni+Nb)-terminated interface with top site and hollow site stacking. The values of bond overlap population are 0.73 and 0.87, respectively, implying that the interfacial region of top site model is weaker than that of the hollow site model. That is to say, the covalent bonding of the hollow site model is stronger at the interface region. Table 5 lists the charge population of the two models. Combining with the previous analysis of density of states, it is clear that electron hybridization for the hollow site model is stronger than that for the top site model at the interface region. Therefore, the hollow site model is more stable.
Table 5 Charge population of Ni (001) and Ni3Nb (001) coherent interfacial section
5 Conclusions
1) Surface convergence calculations reveal that the Ni slabs and Ni3Nb slabs with more than eight atomic layers exhibit bulk-like interior feature. The surface energy for Ni-terminated surface is much smaller than that for (Ni+Nb)-terminated surface, indicating that the latter is more stable than the former.
2) The analyses of work of adhesion and thermal stability demonstrate that the (Ni+Nb)-terminated interface with hollow site stacking has the largest cohesive strength and critical stress for crack propagation and it is the most easily formed interface among the four models.
3) The density of states, charge density difference distribution and charge population suggest that the (Ni+Nb)-terminated interface with hollow site stacking has covalent features across interfacial region between FNN Ni and Nb atoms, especially the covalent interaction of Ni 3d and Nb 4d.
4) The thermal stability of Ni/Ni3Nb (001) interface is worse than that of Ni/Ni3Al (001) interface. But the formation of Ni/Ni3Nb interface can improve the mechanical properties of Ni-based single-crystal superalloys.
References
[1] SIMS C T, STOLOFF N S, HANGEL W C. Superalloys II [M]. New York: Wiley, 1987.
[2] BETTERIDGE W. Nickel and its alloys [M]. United Kingdom: Halsted Press, 1984.
[3] DAI Song-bo, LIU Wen-chang. First-principles study on the structural, mechanical and electronic properties of δ and γ′′ phases in Inconel 718 [J]. Computational Materials Science, 2010, 49(2): 414-418.
[4] ANNARUMMA P, TURPIN M. Structure and high temperature mechanical behavior of Ni-Ni3Nb unidirectional eutectic [J]. Metallurgical Transactions, 1972, 3(1): 137-146.
[5] BANERJEE R, FAIN J P, ANDERSON P M, FRASER H L. Influence of crystallographic orientation and layer thickness on fracture behavior of Ni/Ni3Al multilayered thin films [J]. Scripta Materialia, 2001, 44(11): 2629-2633.
[6] CHEN K, ZHAO L R, TSE J S. Synergetic effect of Re and Ru on γ/γ′ interface strengthening of Ni-base single crystal superalloys [J]. Materials Science and Engineering A, 2003, 360(1-2): 197-201.
[7] CHEN K, ZHAO L R, TSE J S. A first-principles survey of γ/γ′ interface strengthening by alloying elements in single crystal Ni-base superalloys [J]. Materials Science and Engineering A, 2004, 365(1-2): 80-84.
[8] WANG Cong, WANG Chong-yu. Ni/Ni3Al interface: A density functional theory study [J]. Applied Surface Science, 2009, 255(6): 3669-3675.
[9] WANG Jing, ZHANG Lan-ting, CHEN Ke, SUN Nai-rong, SHAN Ai-dang. Morphology and chemical composition of γ/γ′ phases in Re-containing Ni-based single crystal superalloy during two-step aging [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(7): 1513-1517.
[10] PENG L, PENG P, LIU Y G, HE S, WEI H, JIN T, HU Z Q. The correlation between Re and P and their synergetic effect on the rupture strength of the γ-Ni/γ′-Ni3Al interface [J]. Computational Materials Science, 2012, 63: 292-302.
[11] PAYNE M C, TETER M P, ALLAN D C, ARIAS T A, JOANNOPOULOS J D. Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients [J]. Reviews of Modern Physics, 1992, 64: 1045-1097.
[12] SEGALL M D, LINDAN P J D, PROBERT M J, PICKARD C J, HASNIP P J, CLARK S J, PAYNE M C. First-principles simulation: ideas, illustrations and the CASTEP code [J]. Journal Physics: Condensed Matter, 2002, 14(11): 2717.
[13] VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism [J]. Physical Review B, 1990, 41(11): 7892.
[14] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letter, 1996, 77(18): 3865-3868.
[15] FISCHER T H, ALMLOF J. General methods for geometry and wave function optimization [J]. Journal of Physical Chemistry, 1992, 96(24): 9768-9774.
[16] WANG Y, LIU Z K, CHEN L Q. Thermodynamic properties of Al, Ni, NiAl, and Ni3Al from first-principles calculations [J]. Acta Materialia, 2004, 52(9): 2665-2671.
[17] MISHIN Y. Atomistic modeling of the γ and γ′-phases of the Ni-Al system [J]. Acta Materialia, 2004, 52(6): 1451-1467.
[18] QUIST W E, TAGGART R, POLONIS D H. The influence of iron and aluminum on the precipitation of metastable Ni3Nb phases in the Ni-Nb system [J]. Metallurgical Transactions, 1971, 2(3): 825-832.
[19] FIORENTINI V, METHFESSEL M. Extracting convergent surface energies from slab calculations [J]. Journal of Physics: Condensed Matter, 1996, 8(36): 6525-6531.
[20] RAYNOLDS J E, SMITH J R, ZHAO G L, SROLOVITZ D J. Adhesion in NiAl-Cr from first principles [J]. Physical Review B,1996, 53(20): 13883-13889.
Ni(001)/Ni3Nb(001)面界面性质的第一性原理研究
文志勤1，赵宇宏1，侯 华1，王 楠1，傅 利1，韩培德2
1. 中北大学 材料科学与工程学院，太原 030051；2. 太原理工大学 材料科学与工程学院，太原 030024
摘 要：采用第一性原理赝势平面波的方法研究Ni (001)、Ni3Nb (001)表面和Ni/Ni3Nb (001)界面。计算界面终端为Ni或Ni+Nb，堆积方式为顶部位置或空心位置这4种界面模型的粘附功、稳定性及电子结构。结果表明：Ni (001)和Ni3Nb (001)表面具有8个原子层时展现出较好的体相似性；以Ni+Nb为界面终端，堆积方式为空心位置的界面模型具有最大的结合强度和临界裂纹扩展应力，且具有最好的热稳定性。该模型界面处的Ni原子和Nb原子之间是共价键，这主要是由Nb 4d和Ni 3d轨道的电子贡献的。比较Ni/Ni3Nb (001)界面和Ni/Ni3Al (001)界面的性质可知，前者的热稳定性比后者的差，且更难形成界面，但是Ni/Ni3Nb (001)界面的形成能改善镍基合金的力学性能。
关键词：Ni3Nb；第一性原理；界面；电子结构
(Edited by Xiang-qun LI)
Foundation item: Project (2011DFA50520) supported by International Cooperation Project Supported by Ministry of Science and Technology of China; Projects (51204147, 51274175) supported by the National Natural Science Foundation of China; Projects (2011-key6, 2013-81) supported by Research Project Supported by Shanxi Scholarship Council of China; Projects (2013081017, 2012081013) supported by International Cooperation Project Supported by Shanxi Province, China
Corresponding author: Yu-hong ZHAO; Tel: +86-15035172958; E-mail: zyh388@sina.com
DOI: 10.1016/S1003-6326(14)63218-0
Abstract: The Ni (001) surface, Ni3Nb (001) surface and Ni (001)/Ni3Nb (001) interfaces were studied using the first-principles pseudopotential plane-wave method. The adhesion work, thermal stability and electronic structure of Ni/Ni3Nb (001) interfaces were calculated to expound the influence of atom termination and stacking sequence on the interface strength and stability. Simulated results indicate that Ni and Ni3Nb (001) surface models with more than eight atomic layers exhibit bulk-like interior. The (Ni+Nb)-terminated interface with hollow site stacking has the largest cohesive strength and critical stress for crack propagation and the best thermal stability among the four models. This interfacial Ni and the first nearest neighbor Nb atoms form covalent bonds across the interface region, which are mainly contributed by Nb 4d and Ni 3d valence electrons. By comparison, the thermal stability of Ni/Ni3Nb (001) interfaces is worse than Ni/Ni3Al (001) interface, implying that the former is harder to form. But the Ni/Ni3Nb interface can improve the mechanical properties of Ni-based superalloys.
