J. Cent. South Univ. (2017) 24: 2717-2724
DOI: https://doi.org/10.1007/s11771-017-3684-5
Mechanical analysis of double-layered circular graphene sheets as building material embedded in an elastic medium
WU Zheng-tian(吴征天)1, 2, HU Fu-yuan(胡伏原)1, ZHANG Yang(张扬)3,
GAO Qing(高庆)4, 5, CHEN Zhen-ping(陈珍萍)1
1. School of Electronic and Information Engineering,Suzhou University of Science and Technology,Suzhou 215009,China;
2. Department of Systems Engineering and Engineering Management, City University of HongKong,HongKong 999077, China;
3. School of Science, Nanjing University of Science and Technology, Nanjing 210094, China;
4. Institute of Intelligent Machines, Chinese Academy of Sciences, Hefei 230031, China;
5. Department of Automation, University of Science and Technology of China, Hefei 230026, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Abstract:
Possessing the unique and highly valuable properties, graphene sheets (GSs) have attracted increasing attention including that from the building engineer due to the fact that Graphene can be utilized to reinforce concrete and other building materials. In this work, the nonlocal elastic theory and classical plate theory (CLPT) are used to derive the governing equations. The element-free framework for analyzing the buckling behaviors of double layer circular graphene sheets (DLCGSs) relying on an elastic medium is proposed. Pasternak-type model is adopted to describe the elastic medium. Accordingly, the influences of boundary conditions, size of GSs and nonlocal parameters on the buckling behavior of DLCGSs are investigated. The results show that the OP buckling modes are only sensible to the van der Waals forces.
Key words:
1 Introduction
Graphene sheets (GSs) have carbon atomic structure of the monolayer or multilayer atomic thickness. Double layer graphene sheets (DLGSs) constituting a double layer single layer graphene sheet (SLGS) in which the interlayer width is 0.34 nm [1] have specifically chemical, mechanical, thermal and electronic properties [2–5] and are being applied as constituent in nanoelectromechanical systems (NEMS) and micro- electromechanical systems (MEMS). DLGSs used in these applications generally rest on the elastic medium rather than suspension. Thus, understanding the buckling of DLGSs embedded in the elastic media is essential to improve the design and manufacture in engineering.
Applications of DLGSs rely on clear knowledge of their mechanical behavior. In recent years, world-wide researchers have engaged in the study of GSs using experimental, numerical and theoretical tools. However, it is of difficulty to carry out experimental research due to the very small dimensions of the nano-structure elements [6]. Thus, theoretical research is becoming increasingly important for studying nano-structures. The theoretical tools include three categories [7], i.e. atomistic modeling, continuum mechanics and the combination of aforementioned two tools. The atomistic modeling roughly consists of classic tight-binding molecular dynamics (TBMD), molecular dynamics (MD). ANSARI and SAHMANI [8] analyzed the biaxial buckling behavior of SLGSs using atomistic MD simulations. GAJBHIYE and SACHIN et al [9] revealed the nonlinear frequency response of SLGSs by the atomistic finite element method (FEM). Molecular dynamic simulation is limited to the analysis of GSs with few atoms. However, unlike atomic simulation, the continuum mechanics has a lower computational cost [10]. Therefore, some relatively large nanostructures can be analyzed by this method [11, 12]. The classical continuum approach is however a kind of scale-free theory which cannot account for the small scale effect arising in the nanostructures. Therefore, the mechanical behavior of nano-structures cannot be successfully captured by the classical continuum approach. It behooves us to modify the classical continuum model which can describe precise mechanical behaviors of the nano-structures. Some improved continuum methods including couple stress theory [13], surface elasticity theory [14], strain gradient theory [15] and nonlocal theory were used to study the size-dependent materials. It is found that the nonlocal theory provides good matching results compared with lattice dynamics. Recent literature shows that nonlocal elasticity is being progressively used [16–18]. PEDDIESON et al [19] were the first one who adopted the nonlocal theory to analyze the static deformations of Euler-Bernoulli nanobeams. DUAN and WANG [20] firstly formulated the nonlocal continuum plate model to exmanine the size effect via the bending of circular nanoplates. DASTJERDI et al [21] studied the multilayer orthotropic circular GSs nonlinear bending using nonlocal theory. ZHANG et al [7] revealed the free vibration behaviors of DLGSs employing non-local elasticity theory.
Apart from double-layered circular graphene sheets, various types of nanostructures elements such as nanorod, nanobeam, and nanoplates have also been investigated by numerous researchers. SAFARABADI et al [22] proposed Gurtin–Murdoch model combined with surface effects and studied the free vibration behavior of rotating nanobeam. GOODARZI et al [23] studied the free vibration behavior of rectangular graphene sheet under shear in-plane load which was simulated as a visco- Pasternak foundation and obtained numerical solutions for the vibration frequency with differential quadrature method. MOHAMMADI et al [24] investigated the free vibration behavior of orthotropic rectangular grapheme sheet embedded in an elastic medium under biaxial pre-load and investigated the effects of the small scale, pre-load, Winkler and Pasternak foundations and material properties on natural frequencies. The buckling characteristics of nanoscale rectangular plates under bi-axial compression considering nonuniformity in the thickness were studied by FARAJPOUR et al [25].
Numerical techniques are important for theoretical analysis. Various numerical tools have been utilized to examine the mechanical properties of nanostructure. TUNA and KIRCA [26] derived finite element formulations for linear buckling, static bending and free vibration analysis of nanobeam structures by employing the integral form of Eringen nonlocal model. As a numerical technique, the element-free method has been applied in solving engineering problems successfully. Because of its advantage of not relying on elements, it has good adaptability [27–31].
In the present work, the authors investigate the buckling behavior of DLCGSs resting on a Pasternak elastic medium employing the nonlocal theory and meshless method. The effects of nonlocal parameters, geometry size of GSs and foundation parameters on the buckling behavior of circular DLGSs are examined.
2 Nonlocal elasticity theory and model of elastic medium
2.1 Nonlocal theory
ERINGEN et al [32] proposed the nonlocal theory through experiment and the theoretical analysis in which the stress state depends on the strain state of all the points in the domain. Thus, it can reflect small scale effect. The most widely applied constitutive relation ship in the differential form is written as
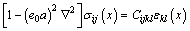 (1)
(1)
where e0a is the nonlocal parameter;  donates the Laplacian operator which is given by
donates the Laplacian operator which is given by
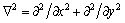 (2)
(2)
2.2 Model of elastic medium.
In nanoscale devices, bucking behaviors can be observed, which affects the performance significantly. As mentioned above, graphene based products are usually resting on an elastic medium. In the present work, the Pasternak-type foundation [33] is adopted. Pasternak- type foundation model is modeled with two parameters. The mathematical expression of Pasternak-type foundation is written as
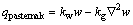 (3)
(3)
where the Winker modulus and the shear modulus of the elastic medium are respectively represented by kw and kg.
3 Theoretical approach
3.1 van der Waals (vdW) force expression
In DLGSs, the interaction force between layers is the van der Waals (vdW) force and is a non-bonded interaction. By neglecting the nonlinear terms, the vdW’s interaction can be expressed as [34]
 (4)
(4)
where cij donates the vdW coefficient. According to Ref. [34], the vdW coefficient is cij=–146.8247 GPa/nm.
3.2 Governing equations
The circular DLGSs resting on an elastic foundation are demonstrated in Fig. 1. The external medium is modeled as Pasternak-type foundation. LR denotes the radius length of GSs. The thickness of graphene is h. Transverse displacements of the top-GSs and bottom- GSs for the buckling analysis are represented by w1(x, y, t) and w2(x, y, t), respectively.

Fig. 1 Circular DLGSs resting on a Pasternak-type elastic medium
Based on the CPL and small deflection assumption, displacements of top-GSs can be written as
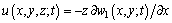 (5)
(5)
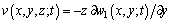 (6)
(6)
 (7)
(7)
where (u, v, w) respectively denote the displacements along the axis (x, y, z); w1 is the displacement along z axis of the mid-plane. According to the strain- displacement relations:
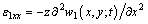 (8)
(8)
 (9)
(9)
 (10)
(10)
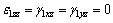 (11)
(11)
with the principle of virtual work, the equilibrium equation can be derived as
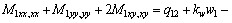
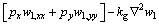 (12)
(12)
The constitutive relationship are given by
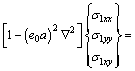
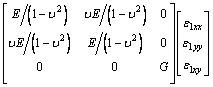 (13)
(13)
According to Eq. (12), the nonlocal moments are
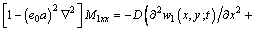
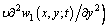 (14)
(14)

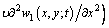 (15)
(15)
 (16)
(16)
where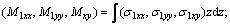 D is the bending stiffness and
D is the bending stiffness and 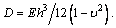
From Eqs. (13)–(15), the following expression is derived as
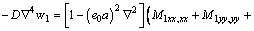
 (17)
(17)
Putting Eq. (16) into Eq. (11), one obtains
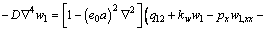
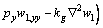 (18)
(18)
Similarly, one can obtain the governing equation of bottom-GSs:
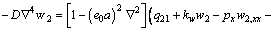
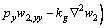 (19)
(19)
4 Discretized system equations
4.1 Weak form
In order to get the weak form, the equilibrium equation is multiplied by the virtual displacement δw, Therefore, it can be obtained as
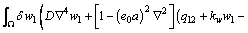
 (20)
(20)
Equation (20) can be integrated by part as
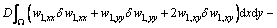
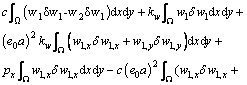
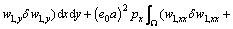
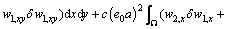
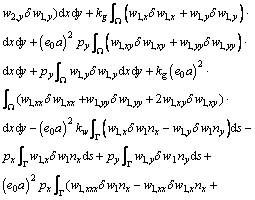
 (21)
(21)
The weak form of Eq. (18) can be written as

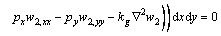 (22)
(22)
Equation (22) can be integrated by part similarly.
4.2 Discrete system equations
Letting λ=px=py, as used in the element-free method, the discrete equation of Eq. (20) can be expressed as
 (23)
(23)
where
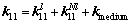 (24)
(24)
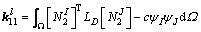 (25)
(25)
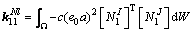 (26)
(26)
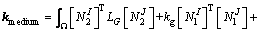
 (27)
(27)
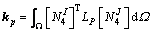 (28)
(28)
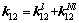 (29)
(29)
 (30)
(30)
 (31)
(31)
Similarly, one can obtained
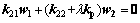 (32)
(32)
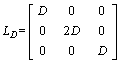 (33)
(33)
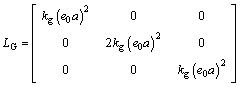 (34)
(34)
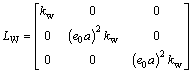 (35)
(35)
 (36)
(36)

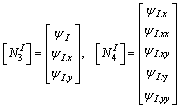 (37)
(37)
By combining Eq. (22) and Eq. (31), one can get
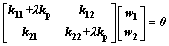 (38)
(38)
Equation (37) can be rewritten as
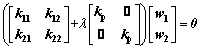 (39)
(39)
By solving eigenvalue problem of Eq. (38), the buckling properties of DLCGSs can be presented.
5 Numerical results and discussion
5.1 Experimental conditions and variable set
The mechanical parameters are the same as Ref. [35], as listed in Table 1. Some non-dimensional parameters are adopted: Winker modulus parameter 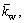 shear modulus parameter
shear modulus parameter 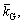 buckling load parameters θ and φ.
buckling load parameters θ and φ.
Table 1 Mechanical properties

The definitions are adopted as
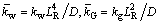 (40)
(40)
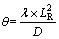 (41)
(41)
 (42)
(42)
5.2 Effect of boundary conditions on buckling load of DLCGSs
To show the effect of boundary conditions on the buckling load of DLCGSs, a simulation is performed on DLCGSs with a radius of 10 nm without elastic foundations. The mechanical properties of GSs are: E=1.06 TPa, υ=0.25, h=0.34 nm, the density ρ=2.25×103 kg/m3 and the nonlocal parameter (e0a)2=1.85 nm2. The buckling load parameters of DLCGSs are depicted in Fig. 2. Herein, boundary conditions are represented by symbolic notations. For example, the symbolic notations SSSS denote DLCGSs in which all edges are simply supported along the circumference.
Figures 2 (a) and (b) illustrate the buckling load parameter for in-phase (IP) modes and out-of -phase (OP) modes under different boundary conditions, respectively. As can be seen in Fig. 2(a), the buckling load parameters under different boundary conditions increase as the IP modes increase. This phenomenon is similar with that in SLCGSs. By comparison, the buckling load parameters decrease with the increasing of OP buckling modes under all boundary conditions. Moreover, for IP buckling mode, the buckling load parameters under CCCC boundary conditions in the same buckling mode are higher than those under other boundary conditions. However, as for OP buckling mode, the buckling load parameters under SSSS boundary conditions in the same buckling mode is higher than those under other boundary conditions.

Fig. 2 Effect of boundary conditions on buckling load of circular DLGSs with a radius length 10 nm 
5.3 Influence of radius on buckling load parameter of DLCGSs
To study the influence of geometry size on the buckling load of DLCGSs under axial compression with SSSS boundary condition, a simulation is performed without elastic medium. The buckling load parameters changing with the increase of radius length are shown in Fig. 3.
From Fig. 3(a), it is evident that the buckling load parameters increase with the increasing of radius length of circular DLGSs for IP buckling modes. However, for higher IP modes, the buckling load parameters growth rates become slow. It can also be seen that the buckling load parameters for IP buckling mode are higher than other IP buckling modes. The relationship between the radius length of circular DLGSs and the buckling load parameters for OP modes is similar to that for IP modes, as shown in Fig. 3(b). It is obvious that the buckling load parameters in OP modes are much higher than those for IP buckling modes under the same conditions due to the vdW forces.
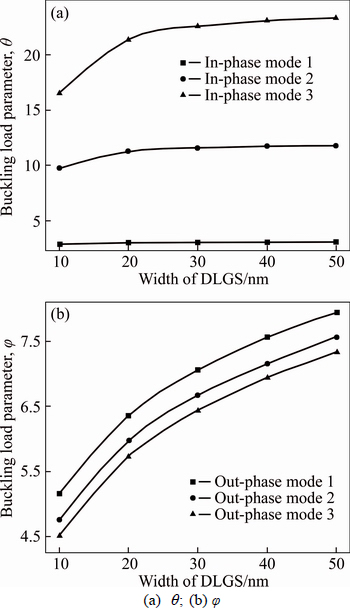
Fig. 3 Effect of radius length on buckling load of simply-supported circular DLCGSs 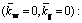
5.4 Effect of nonlocal parameter on buckling load parameter of DLCGSs
Then, the effect of nonlocal parameter on buckling properties of DLCGSs is investigated. Herein, the circular DLGSs under SSSS boundary condition have 10 nm radius length and the influence of elastic medium is not taken into account. Figures 4(a) and (b) give the variation of the buckling load with the increase of nonlocal parameters for IP modes and OP modes, respectively.
Form Fig. 4(a), it is indicated that the buckling load decreases as the nonlocal parameters for IP buckling modes increase. One also can notice that the buckling load parameters of circular DLGSs for higher IP modes are affected more by the nonlocal parameter compared with those for lower IP modes. However, as shown in Fig. 4(b), the buckling load parameters for OP buckling modes are less affected by nonlocal parameters. This phenomenon can also be attributed to the internal forces between layers.
Fig. 4 Influence of nonlocal parameter on buckling load of simply-supported DLCGSs 
5.5 Effect of elastic medium on buckling load parameter of DLCGs
To study the effects of Pasternak elastic foundation on the buckling behavior of circular DLGSs, a case is simulated on a circular DLGSs with radius length of 10 nm under SSSS boundary conditions.
For Figs. 5(a) and (b), the shear modulus parameter is  . It can be seen from Fig. 5(a) that the buckling load parameters go up linearly with the increase of
. It can be seen from Fig. 5(a) that the buckling load parameters go up linearly with the increase of 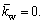 Specially, for IP buckling mode 1, the buckling load increases notably as the Winker modulus increases. It is proved from Fig. 5(b) that the load parameters for OP buckling modes are less influenced by the Winker modulus parameters.
Specially, for IP buckling mode 1, the buckling load increases notably as the Winker modulus increases. It is proved from Fig. 5(b) that the load parameters for OP buckling modes are less influenced by the Winker modulus parameters.
Figures 6(a) and (b) show the relationship between the buckling load parameters and shear modulus parameter for IP and OP modes, respectively. The Winker modulus parameter is Figure 6(a) indicates that the buckling load parameters also increase linearly with the increase of
Figure 6(a) indicates that the buckling load parameters also increase linearly with the increase of 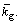 However, the load parameters for OP buckling modes are less affected by the shear modulus parameters. Therefore, the transverse shear deformation of elastic foundation should be taken into account.
However, the load parameters for OP buckling modes are less affected by the shear modulus parameters. Therefore, the transverse shear deformation of elastic foundation should be taken into account.
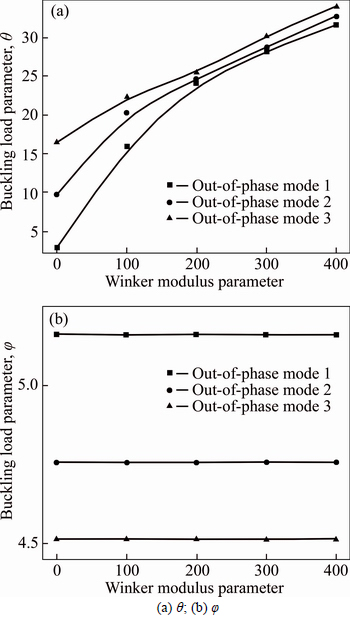
Fig. 5 Effect of winker modulus parameter 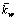 on buckling load of simply-supported DLCGSs:
on buckling load of simply-supported DLCGSs:
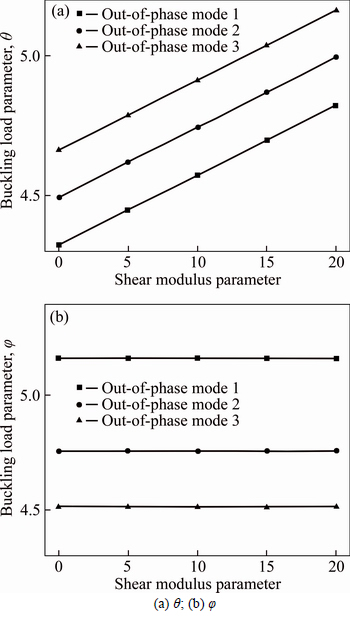
Fig. 6 Effect of shear modulus parameter 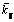 on buckling load of simply-supported DLCGSs
on buckling load of simply-supported DLCGSs 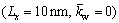 :
:
6 Conclusions
1) The buckling load parameters in OP modes are much higher than those for 2P buckling modes under the same conditions.
2) The buckling load parameters for OP buckling modes are less affected by non-local parameters and Winker modulus parameters.
3) The nonlocal parameter has a significant effect on the buckling load of DLCGSs for synchronous buckling modes.
The present method provides framework for solving mechanical problems rising from the nano device and can be extended to triple layered graphene sheets with more complex service conditions, such as in the magnetic field.
References
[1] SAKAEEPOUR A, AHMADIAN T, VAFAI A. Potential application of single-layered graphene sheet as strain sensor [J]. Solid State Communications, 2008, 147(7, 8): 336–340.
[2] DEMCZYK G, WANG M, CUMINGS J, HETMAN M, HAN W, ZETTL A, RITCHIE O. Direct mechanical measurement of the tensile strength and elastic modulus of multiwalled carbon nanotubes [J]. Materials Science & Engineering A, 2002, 334(1, 2): 173–178.
[3] SHAO Y, WANG J, WU H, LIU J, AKSAY A, LIN Y. Graphene based electrochemical sensors and biosensors: A review [J]. Electroanalysis, 2010, 22(10): 1027–1036.
[4] NETO C. The electronic properties of grapheme [J]. Vacuum, 2007, 83(10): 1248–1252.
[5] YAN J, LIEW K, HE L. Free vibration analysis of single-walled carbon nanotubes using a higher-order gradient theory [J]. Journal of Sound and Vibration, 2013, 332(15): 3740–3755
[6] YAO N, LORDI V. Young’s modulus of single-walled carbon nanotubes [J]. Journal of Applied Physics, 1998, 84(4): 1939–1943
[7] ZHANG Y, ZHANG L, LIEW K, YU J. Free vibration analysis of bilayer graphene sheets subjected to in-plane magnetic fields [J]. Composite Structures, 2016: 144: 86–95.
[8] ANSARI R, SAHMANI S. Prediction of biaxial buckling behavior of single-layered graphene sheets based on nonlocal plate models and molecular dynamics simulations [J]. Applied Mathematical Modelling, 2013, 37(12, 13): 7338–7351.
[9] GAJBHIYE O, SINGH P. Multiscale nonlinear frequency response analysis of single-layered graphene sheet under impulse and harmonic excitation using the atomistic finite element method [J]. Journal of Physics D Applied Physics, 2015, 48(14): 1–16.
[10] ARASH B, WANG Q. A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphemes [J]. Computational Materials Science, 2012, 51(1): 303–313.
[11] YAKOBSON I, BRABEC J, BERNHOLC J. Nanomechanics of Carbon Tubes: Instabilities beyond linear response [J]. Physical Review Letters, 1996, 76(14): 2511–2514.
[12] KRISHNAN A, DUJARDIN E, EBBESEN T W, YIANILOS P N, TREACY M M J. Young’s modulus of single-walled nanotubes [J]. Physical Review B, 1998, 58(20): 14013–14019.
[13] YANG F, CHONG M, LAM C, TONG P. Couple stress based strain gradient theory for elasticity [J]. International Journal of Solids and Structures, 2002, 39(10): 2731–2743.
[14] LU P, HE H, LEE P, LU C. Thin plate theory including surface effects [J]. International Journal of Solids and Structures, 2006, 43(16): 4631–4647.
[15] FLECK A, HUTCHINSON W. Strain gradient plasticity [J]. Acta Metallurgica et Materialia, 1997, 42(2): 295–361.
[16] MALEKZADEH P, SETOODEH R, ALIBEYGI A. Small scale effect on the thermal buckling of orthotropic arbitrary straight-sided quadrilateral nanoplates embedded in an elastic medium [J]. Composite Structures, 2011, 93(8): 2083–2089.
[17] ZENKOUR M, SOBHY M. Nonlocal elasticity theory for thermal buckling of nanoplates lying on Winkler–Pasternak elastic substrate medium [J]. Physica E: Low-dimensional Systems and Nanostructures, 2013, 53: 251–259.
[18] MOHAMMADI M, FARAJPOUR A, MORADI A, GHAYOUR M. Shear buckling of orthotropic rectangular graphene sheet embedded in an elastic medium in thermal environment [J]. Composites Part B: Engineering, 2014, 56: 629–637.
[19] PEDDIESON J, BUCHANAN R, MCNITT P. Application of nonlocal continuum models to nanotechnology [J]. International Journal of Engineering Science, 2003, 41(3–5): 305–312.
[20] DUAN H, WANG M. Exact solutions for axisymmetric bending of micro/nanoscale circular plates based on nonlocal plate theory [J]. Nanotechnology, 2007, 18(38): 450–450.
[21] DASTJERDI S, JABBARZADEH M. Non-linear bending analysis of multi-layer orthotropic annular/circular graphene sheets embedded in elastic matrix in thermal environment based on non-local elasticity theory [J]. Applied Mathematical Modelling, 2017, 41: 83–101.
[22] SAFARABADI M, MOHAMMADI M, FARAJPOUR A, GOODARZI M. Effect of surface energy on the vibration analysis of rotating nanobeam [J]. Journal of Solid Mechanics, 2015, 7(3): 299–311.
[23] GOODARZI M, MOHAMMADI M, FARAJPOUR A, KHOORAN M. Investigation of the effect of pre-stressed on vibration frequency of rectangular nanoplate based on a visco pasternak foundation [J]. Journal of Solid Mechanics, 2014, 6: 98–121.
[24] MOHAMMADI M, GOODARZI M, GHAYOUR M, ALIVAND S. Small scale effect on the vibration of orthotropic plates embedded in an elastic medium and under biaxial in-plane pre-load via nonlocal elasticity theory [J]. Journal of Solid Mechanics, 2012, 4(2): 128–143.
[25] FARAJPOUR A, DANESH M, MOHAMMADI M. Buckling analysis of variable thickness nanoplates using nonlocal continuum mechanics [J]. Physica E: Low-dimensional Systems and Nanostructures, 2011, 44(3): 719–727.
[26] TUNA M, KIRCA M. Bending, buckling and free vibration analysis of Euler Bernoulli nanobeams using Eringen’s nonlocal integral model via finite element method [J]. Composite Structures, 2017, 179: 269–284.
[27] ZHANG L, DENG Y, LIEW K. An improved element-free Galerkin method for numerical modeling of the biological population problems [J]. Engineering Analysis with Boundary Elements, 2014, 40181–4188.
[28] LIEW K, LEI Z, YU L, ZHANG L. Postbuckling of carbon nanotube-reinforced functionally graded cylindrical panels under axial compression using a meshless approach [J]. Computer Methods in Applied Mechanics and Engineering, 2014, 26: 81–17.
[29] LEI Z, LIEW K, YU J. Free vibration analysis of functionally graded carbon nanotube-reinforced composite plates using the element-free kp-Ritz method in thermal environment [J]. Composite Structures, 2013, 106: 128–138.
[30] ZHANG Y, LEI Z, ZHANG L, LIEW K, YU J. Nonlocal continuum model for vibration of single-layered graphene sheets based on the element-free kp-Ritz method [J]. Engineering Analysis with Boundary Elements, 2015: 5690–5697.
[31] ZHANG L, ZHANG Y, LIEW K, Vibration analysis of quadrilateral graphene sheets subjected to an in-plane magnetic field based on nonlocal elasticity theory [J]. Composites Part B: Engineering, 2017, 118: 96–103.
[32] ERINGEN C, ERINGEN C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves [J]. Journal of Applied Physics, 1983, 54(9): 4703–4710.
[33] PASTERNAK P. On a new method of analysis of an elastic foundation by means of two foundation constants [M]. Moscow: Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstvu i Arkhitekture, 1954.
[34] JOMEHZADEH E, SAIDI R, PUGNO M. Large amplitude vibration of a bilayer graphene embedded in a nonlinear polymer matrix [J]. Physica E: Low-dimensional Systems and Nanostructures, 2012, 44(10): 1973–1982.
[35] MURMU T, SIENZ J, ADHIKARI S, ARNOLD C. Nonlocal buckling of double-nanoplate-systems under biaxial compression [J]. Composites Part B Engineering, 2013, 44(1): 84–94.
(Edited by DENG Lü-xiang)
Cite this article as:
WU Zheng-tian, HU Fu-yuan, ZHANG Yang, GAO Qing, CHEN Zhen-ping. Mechanical analysis of double-layered circular graphene sheets as building material embedded in an elastic medium [J]. Journal of Central South University, 2017, 24(11): 2717–2724.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-017-3684-5Foundation item: Project(30917011339) supported by the Fundamental Research Funds for the Central Universities, China; Project(BK20170820) supported by the Natural Science Foundation of Jiangsu Province, China; Projects(61472267, 71471091, 71271119) supported by the National Natural Science Foundation of China; Project(17KJD110008) supported by the Natural Science Fund for Colleges and Universities in Jiangsu Province, China; Project(BE2017663) supported by the Key Research & Developement Plan of Jiangsu Province, China
Received date: 2017-08-30; Accepted date: 2017-11-02
Corresponding author: CHEN Zhen-ping, PhD; Tel: +86–15150428661; E-mail: zhpchen@mail.usts.edu.cn
Abstract: Possessing the unique and highly valuable properties, graphene sheets (GSs) have attracted increasing attention including that from the building engineer due to the fact that Graphene can be utilized to reinforce concrete and other building materials. In this work, the nonlocal elastic theory and classical plate theory (CLPT) are used to derive the governing equations. The element-free framework for analyzing the buckling behaviors of double layer circular graphene sheets (DLCGSs) relying on an elastic medium is proposed. Pasternak-type model is adopted to describe the elastic medium. Accordingly, the influences of boundary conditions, size of GSs and nonlocal parameters on the buckling behavior of DLCGSs are investigated. The results show that the OP buckling modes are only sensible to the van der Waals forces.


