DOI:https://doi.org/10.1007/s11771-021-4740-8
J.Cent.South Univ.(2021) 28: 2407－2422
Adaptive sampling approach based on Jensen-Shannon divergence for efficient reliability analysis
CHEN Liang-jun(陈良军)1, HONG Yu(洪彧)2, Sujith MANGALATHU3,GOU Hong-ye(勾红叶)1, PU Qian-hui(蒲黔辉)1
1. Department of Bridge Engineering, School of Civil Engineering, Southwest Jiaotong University,Chengdu 610031, China;
2. National Engineering Laboratory for Technology of Geological Disaster Prevention in Land Transportation, Southwest Jiaotong University, Chengdu 611756, China;
3. Research Scientist, Equifax Inc, Alpharetta 30309, USA
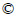Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract:
Extensive studies have been carried out for reliability studies on the basis of the surrogate model, which has the advantage of guaranteeing evaluation accuracy while minimizing the need of calling the real yet complicated performance function. Here, one novel adaptive sampling approach is developed for efficiently estimating the failure probability. First, one innovative active learning function integrating with Jensen-Shannon divergence (JSD) is derived to update the Kriging model by selecting the most suitable sampling point. For improving the efficient property, one trust-region method receives the development for reducing computational burden about the evaluation of active learning function without compromising the accuracy. Furthermore, a termination criterion based on uncertainty function is introduced to achieve better robustness in different situations of failure probability. The developed approach shows two main merits: the newly selected sampling points approach to the area of limit state boundary, and these sampling points have large discreteness. Finally, three case analyses receive the conduction for demonstrating the developed approach’s feasibility and performance. Compared with Monte Carlo simulation or other active learning functions, the developed approach has advantages in terms of efficiency, convergence, and accurate when dealing with complex problems.
Key words:
reliability; Monte Carlo; Kriging model; Jensen-Shannon divergence; trust-region；
Cite this article as:
CHEN Liang-jun,HONG Yu, Sujith MANGALATHU, GOU Hong-ye, PU Qian-hui. Adaptive sampling approach based on Jensen-Shannon divergence for efficient reliability analysis [J]. Journal of Central South University, 2021, 28(8): 2407-2422.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-021-4740-81 Introduction
Engineering structures are subjected to unavoidable uncertainties, such as material properties, geometry, applied loads, and manufacturing imperfection. The uncertainties may dramatically influence the safety and performance of structures. A reliability study is conducted for assessing the safety of structures considering uncertainties, as well as supporting reliability-based design optimization [1-3]. Typically, performance function is utilized to characterize the behavior of a structure: a negative value indicates failure, and a positive value means safety. The boundary between failure and safe domains is the limit state. Failure probability is generally used to evaluate structural reliability, which implies that the performance function is less than or equal to 0. Practically, the performance function generally exhibits the non-linearity and even implicitness. Thus, the high-dimensional integral based on the performance function is difficult to be assessed directly. Therefore, in structural reliability analysis, it is a significant challenge to evaluate the failure probability at the cost of as little computational burden as possible while ensuring high accuracy.
Present reliability analyses, are mainly approximate methods and simulation approaches. In the approximate methods, the first-order reliability method (FORM) [4] and the second-order reliability method (SORM) [5, 6] have wide utilization to approximate the failure probability. These are capable of approximating the failure probability with a point of the highest possibility on the surface of the limit state according to the first- or second-order Taylor expansion, regardless of higher-order terms. FORM and SORM show reasonable efficiency for uncomplicated non-linear limit states, whereas they have inaccuracy under great non-linear property or several designing points [7]. Monte Carlo simulation (MCS) approaches are capable of presenting outcomes exhibiting an arbitrary accuracy, which are different from the approximate methods, so MCS methods are generally used as a benchmark result for evaluating other methods’accuracy and efficiency [8]. The precise estimating process for the failure probability pertaining to a structure or system usually needs considerable samples and limit state evaluations. Variance reduction techniques have been used for reducing the statistics-related fluctuating processes and yielding results with more preciseness, e.g., subset simulation [9], directional simulation [10], line sampling [11], as well as importance sampling [12]. However, the computation efficiency of those methods is still limited in real problems that involve complicated finite element analysis.
The surrogate model technique has been proven as a promising alternative, which is frequently applied in multi-disciplinary design optimization. The notion of utilizing a surrogate model for representing one complicated system phenomenon is increasingly popular in recent years [13]. The surrogate model refers to one approximation function pertaining to the input-output relationship, and it can generally be established via design of experiment (DoE). The approximation function can be applied for replacing the original complex model, as an attempt at improving the computation efficient property in the optimization process. Some surrogate model categories have been established to conduct reliability analysis [14-17]. Kriging model, as one of the most promising representatives, is suitable for multi-parameter optimization [18].
In the literature, active learning reliability analysis has been conducted by integrating the Kriging model and crude Monte Carlo Simulation method (AK-MCS) and demonstrated multiple merits, such as high accuracy and efficiency. Prior researches on the AK-MCS-based reliability study are able to fall to three types.
The first kind aims at improving the active learning function to adaptively and effectively improve the accurate property pertaining to the failure probability. Given the diversification of structure-related reliability study and global optimizing process, BICHON et al [19] built a novel active learning function EFF to search new sampling points that are located around the limit state or with large variance in the entire design space. Thus, the EFF can conduct the efficiency-based global reliability analysis. However, massed sample points are needed, as it is likely to take the points which exhibiting significantly low probability density. ECHARD et al [20] developed a new active learning function U to perform the AK-MCS method. This new function U highlighted the probability of misclassification about the performance function’s sign attributed to the Kriging model, instead of the estimated variance. Nevertheless, it is likely to lose several critical information. An active learning function H combining with information entropy theoretical grounds was developed by LU et al [21], it has the capability to quantify uncertainty. To quantify the risk of incorrect estimation of the sign at the candidate sampling point, the expected risk function (ERF) was developed by YANG et al [22]. The least improvement function (LIF) was developed by SUN et al [23], it can quantify the extent of improvement pertaining to the accuracy of the reliability analysis when a new sample is added, it takes advantage of statistics-related information presented from the Kriging model, as well as considering input variables’joint probability density function. But its formulation is significantly complex, containing one numerical integration under the uneven number of input variables, thereby causing elevated computation-related cost. ZHANG et al [24] yielded two new active learning functions termed as expected improvement function (REIF) and REIF2 on basis of the folded-normal theory, and they can estimate the failure probability in an effective manner.
The second category aims at studying various sampling region strategies. YUN et al [25] developed the adaptive radial algorithm combining with importance sampling for decreasing candidate points that are evaluated, and the concept is to find the optimal-sphere, i.e., the greatest safe domain sphere. Subsequently, samples within the optimal-sphere receives the direct recognition to be safe and are not required for calling the performance function in term of the judgement of their states (safe or failed). WEN et al [26] constructed an adaptive sampling strategic procedure to avoid the selection of the samples in regions in which input variables exhibit low joint probability density function, and developed two parallel strategies to select several training points in the respective iteration. WANG et al [27] proposed the maximum error rate by complying with the Lindeberg condition under Central Limit theorem to analyze reliability, as well as establishing one feasible sampling region based on the proposed method. JIANG et al [3] developed a novel methodology based on a global estimated error of the failure probability and Voronoi diagram, as an attempt at estimating the failure probability and rapidly updating the surrogate model.
The third category has an aim to study the termination criterion. Currently, most of the existing learning functions use preset target thresholds as the termination criterion, which is not suitable for all situations. HU et al [28] utilized the maximal percentage error below a limit predefined as a termination criterion for conducting time-dependent reliability analyzing process. SUN et al [23] used the uncertainty function of failure probability as the condition of convergence.
As aforementioned, it is still a challenge for balancing AK-MCS’s accurate and efficient properties in the case of complicated finite element analysis. The present study develops a novel adaptive sampling approach for efficiently analyzing the reliability. First, an innovative active learning function based on Jensen-Shannon divergence (JSD) is derived to adaptively choose the most suitable sampling points and update the Kriging model. The JSD measures the distance between two probabilistic distributions and has been applied in many applications, such as sensor data fusion [29], and machine learning. Unlike the Kullback-Leibler (KL) divergence [30], the JSD benefits from boundedness and symmetry. Besides, the JSD does not suffer from numerical under/overflow during the optimization process. Second, since a lot of candidate points require the assessment for searching the best next sampling point, this may increase the evaluation time and sometimes result in insufficient computer memory. Therefore, a trust-region method is proposed to decrease the computational cost of the active learning function and without influencing the estimated accuracy of failure probability. Third, the termination criterion based on the uncertainty function is introduced.
The remaining chapters of this article are arranged as follows. Section 2 overviews the background, including the Kriging model and fundamental theory of AK-MCS. Section 3 introduces the developed adaptive sampling approach. Section 4 illustrates the algorithm framework of the developed approach. The feasibility and performance of the developed approach are demonstrated by three cases in Section 5. Section 6 presents some concluding remarks.
2 Background
2.1 The kriging model
The Kriging method [31] refers to a model of interpolation, whose interpolation result is a linear weighting of the known sampling points, as shown in Eq. (1):
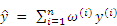
To acquire the weighting coefficients 
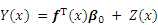
where f T(x) is a vector of regression functions (or basic functions); β0 represents the regression parameters vector; fT(x)β0 is also known as a global trend variable, representing the mathematical expectation of Y(x); Z(x) represents a static stochastic process with zero mean and variance of σ2. The prediction result of each point through the Kriging model obeys Gaussian distribution, as shown in Figure 1.
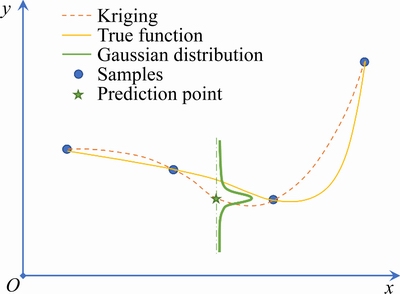
Figure 1 Schematic of Kriging model
These random variables have correlations at different points in the design space. This correlation can be presented as a covariance:
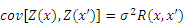
where R(x, x′) represents a correlation function, which is related to the spatial distance of two points. Different correlation functions will lead to different prediction results of the Kriging model. The present study chooses the Gaussian exponential correlation model, whose expression is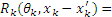 
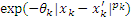
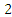
Based on the above statistical assumptions, when the minimum mean square deviation and the following unbiased conditions are satisfied, the formulation of predicted value can be expressed as follow [13]:
where R denotes a matrix consisting of correlation functions between all known sampling points; r represents the correlation vector, which consists of a correlation function between the unknown sampling point and the known sampling points; F=[f T(x(i))]m×p; ys=[y(1) y(2) …y(i)], y(i) is the function response value coresponding to the sample point. Also, the Kriging model’s unique variance estimation function can give an estimate of the mean square error (MSE):
This MSE is capable of being employed for guiding new sample points’ adding process for improving the Kriging model’s predicting accuracy.
2.2 Reliability analysis based on AK-MCS
Theoretically, the definition of the failure probability Pf can be given as follows:
where x is the input variables which affect the safety and performance of structure; and f(x) is the joint probability density function of input variables.
When x denotes high dimensional, or when the performance function exhibits a high degree of non-linearity, it is quite difficult or unlikely to address equations by the numerical integration. The MCS is the most reliable means for estimating the failure probability by utilizing the failure rate of the random samples. To be specific, a sample population of size nmc is generated, and its performance function is assessed. Subsequently, the failure probability Pf is determined as following:
where I(G(xi)) denotes a failure indicator function:
The coefficient of variation (COV) of Pf is
In the reliability analysis, the MCS algorithm has to repeatedly evaluate the performance function. With the increasing reliability of engineering structures or system, their failure become a rare event. Therefore, the MCS algorithm tends to need considerable performance function evaluations for estimating Pf, probably requiring huge calculation times, particularly in terms of engineering structures with implicit and complex performance functions.
3 Developed approach
3.1 Novel active learning function
In this section, an innovative active learning function based on JSD will be derived. This function is helpful for choosing the most suitable sampling points to effectively improve the Kriging model. This JSD is one measurement for the distance between two or more probability distributions based on information theory introduced by LIN [32]. The definition of the JSD is described as follows.
With a continue random variable t, if P1 and P2 are two probability distributions for t. The JSD between P1 and P2 is denoted as:
where P0 is the mixture distribution of (P1+P2)/2; and KL is the Kullback-Leibler divergence. The KL divergence of the given two probability distribution P1 and P2 can be expressed as follow:
There are some fundamental properties for the JSD [30]:
1) JSD is symmetric and always well-defined;
2) JSD is bounded: 0≤
3) The square root of JSD satisfies the triangle inequality.
The divergence value is theoretically equal to zero, when the two considered probability density functions are exactly the same.
According to the fundamental concepts elaborated in Section 2.1, the prediction result 
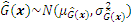
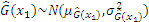
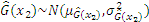
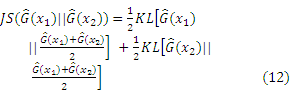
Subsequently, Eq. (12) can be derived as follows:
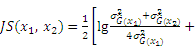
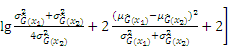
The appendix shows the exhaustive process of derivation from Eqs. (12) to (13).
Because only the sign change of the performance function could impact the estimated accuracy of reliability analysis, the new point chosen by the active learning function should be located near the limit state boundary, that is, the predicted value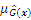 
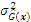
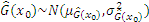
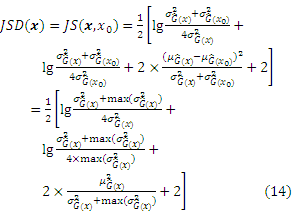
The appendix shows the exhaustive derivation process of the learning function JSD.
Subsequently, the sample points that minimize the active learning function JSD are choosen for updating the Kriging model:
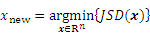
3.2 New trust-region method
To obtain a highly accurate failure probability, considerable samples are required in the AK-MCS algorithm. These enormous candidate sampling points make the evaluation of active learning function time-consuming, such as the active learning functions that include numerical integration. This may increase the computational burden in the reliability analysis procedure, or even make the computer out of memory. Therefore, in this section, a trust-region method is developed to decrease the population of the candidate sample for active learning function evaluation in the AK-MCS algorithm.
The probability of misclassification Pw has been presented [33]. The new sampling points selected by the active learning function should locate around the region of higher probability of Pw. Therefore, the trust-region method only evaluates these sample points that satisfy the following condition without impacting the estimated accuracy of failure probability.
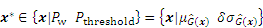
where Pthreshold represents a predetermined threshold, and δ is a parameter equivalent to Pthreshold. The candidate sample pool used for the evaluation of the active learning function would be smaller when the value of δ is smaller.
3.3 Termination criterion
Another key aspect of the active learning function is the termination criterion. The termination criterion which was proposed by SUN et al [23] is introduced as the condition of convergence of the newly developed approach in the present study:
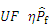
where η is a threshold based on the validations by some examples; Uncertainty function (UF) can be applied to measure the accuracy of 
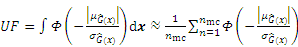
When the UF shows the converging to 0, the 
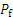
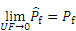
Therefore, the estimated failure probability can be regarded to be accurate when the uncertainty function is small enough.
3.4 Parameter discussion
The developed adaptive sampling approach contains two adjustable parameters, δ and η, which will affect the accuracy and efficiency of the reliability analysis. Therefore, these two parameters are briefly discussed and studied in this section. The numerical case I in Section 5.1 was implemented to research the influence of adjustable parameters. Its performance function is shown in Eq. (20) and the selection of initial random sample points is the same as in Section 5.1.
The parameter η is related to whether the learning function JSD could converge. To investigate the influence of parameter η (the value range of the parameter η is 0 to 1), η=0.0001, 0.001, 0.01, 0.1, 0.2 and 0.5 are selected and numerical analysis is performed. At this time the parameter δ is set to 1. The estimated failure probability (Pf) and corresponding computational cost (the CPU-time consumed) respectively shown in Figures 2(a) and (b). It is seen that the computational cost (the CPU-time consumed) decreases with the increase of the parameter η, but the accuracy of the failure probability decreases with the increase of the parameter η. Considering the accuracy and efficiency of reliability analysis, the parameterη=0.01 is reasonable.
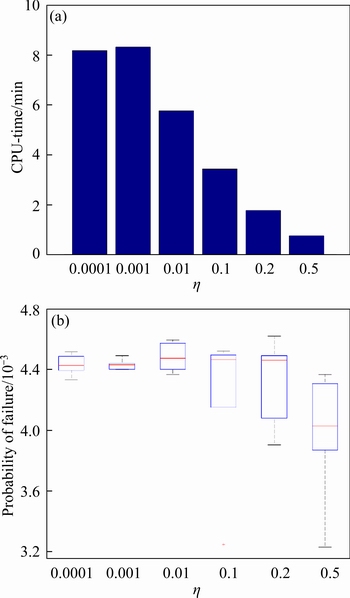
Figure 2 (a) Computational cost and (b) failure probability under different η
According to the definition in Section 3.2, parameter δ mainly affects the efficiency of the developed approach. To investigate the influence of parameter δ (δ≥
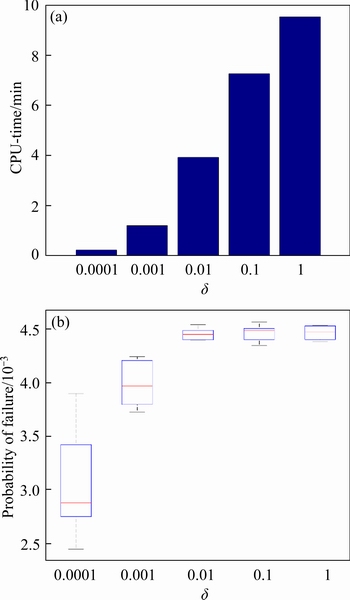
Figure 3 (a) Computational cost and (b) failure probability under different δ
Based on the above analysis, η=0.01 and δ=0.1 are selected for all cases in Section 5.
4 Estimation process of developed approach
The estimation process is illustrated in Figure 4 and depicted below:
Step 1: Generate the candidate samples by the MCS in the design space. nmc candidate sampling points are generated by the MCS method in the design space. In this step, no sample point is assessed through the performance function.
Step 2: Define the initial sample pool for the DoE. Here, the Latin hypercube sample (LHS) technique will be used to select the initial sample pool S1 from the design space, then the initial surrogate model could be constructed. In this step, these selected sample points will be assessed about the real performance function.
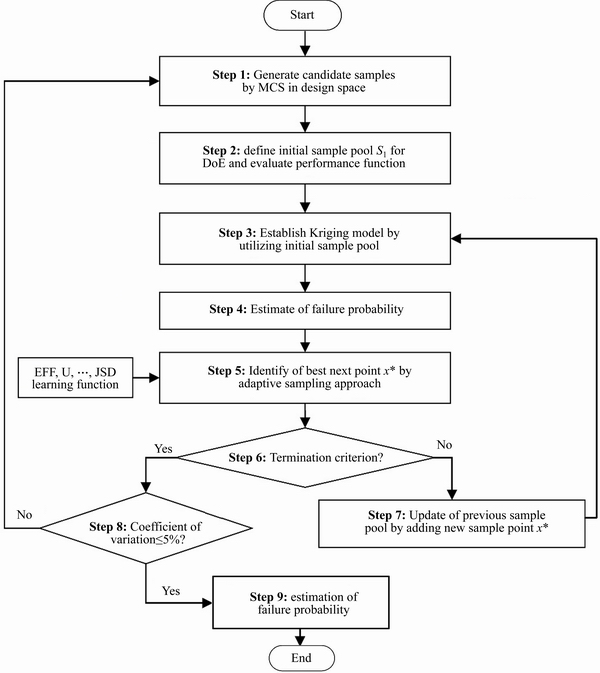
Figure 4 Flowchart of developed approach
Step 3: Establish the Kriging model by utilizing the initial sample pool. In this stage, the Gaussian model is chosen as the correlation function, and the regression function is taken as a constant value. Then, the performance function value and variance of all sample points (i=1, 2, …, nmc) can be predicted.
Step 4: Estimate the failure probability. According to the definition, the
Step 5: Identify the best next sample point. This stage is the core of the reliability analysis process, and should implement the active learning function JSD. Then the JSD value is calculated for each point. The optimal next sample point x* is selected according to Eq. (15).
Step 6: Termination criterion on active learning function. Once the optimal new sample point x* is chosen, its corresponding active learning function’s value will receive the comparison with the termination condition (Eq. (17)).
Step 7: Update of the previous sample pool by adding the new sample point. The optimal new sample point x* needs to be assessed about the real performance function, when the termination criterion at the step 6 is not satisfied. The initial sample pool is updated by adding the best sample point. Steps 3-7 are repeated till the termination criterion is satisfied.
Step 8: Compute the COV of the failure probability. The active learning function JSD will stop when the termination criterion of stage 6 is satisfied. This means the accuracy of the Kriging model is sufficient. This step is to verify whether the count of candidate samples is sufficient to obtain a low COV. Generally, the acceptable threshold for the COV is 5% (Eq. (9)).
Step 9: Update of the candidate sample population or end of reliability analysis. When the COV is too high, the candidate sample population should be rise through the MCS method. If yes, it should be directed to step 4. Otherwise, the AK-MCS algorithm is terminated.
5 Numerical and engineering cases
Three cases are carried out to research the efficiency and accuracy of the developed approach under different situations. The solutions obtained through the MCS method and the active learning function EFF, U, H [19-21], REIF, REIF2 [24] are also provided. The definitions and formulations of their performance function and termination criteria could be found in Refs. [19-24]. The first numerical case (Section 5.1) was studied to explore the behaviors of the new approach. They were chosen for their system reliability and quite complicated performance function. Afterward, a non-linear analytical function was tested (Section 5.2). Finally, an engineering case was studied to prove the application of the developed approach in industrial problems (Section 5.3). These algorithm programs estimating the failure probability are repeated ten times, and the final results are acquired by applying the average of the ten results. To investigate the computational cost of the developed approach and other reported active learning functions, all the solutions in this study are implemented by applying the identical computer, which is equipped with Inter (R) Core i5-7400 CPU processor and 16 GB RAM.
5.1 Numerical case I
The first analytical case has already been widely adopted to demonstrate the system reliability probability problems [9, 20]. It is a series system with four branches, and the performance function is shown as follows:
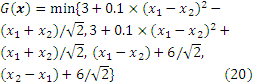
where x = [x1 x2]T is the input variables; and the variables xi are mutually independent standard normal distribution.
All the results by using the MCS method,AK-MCS methods (including EFF, U, H, REIF, REIF2), and the novel developed approach are presented in Table 1, including the total number of calls to the real performance function (Ncall), the estimated failure probability (Pf), the COV of estimated failure probability, and estimated maximum error rate (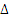
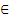
Table 1 Reliability analysis results of different methods in numerical case I
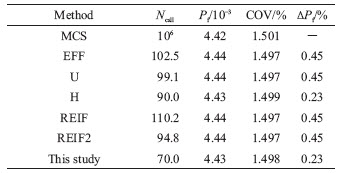
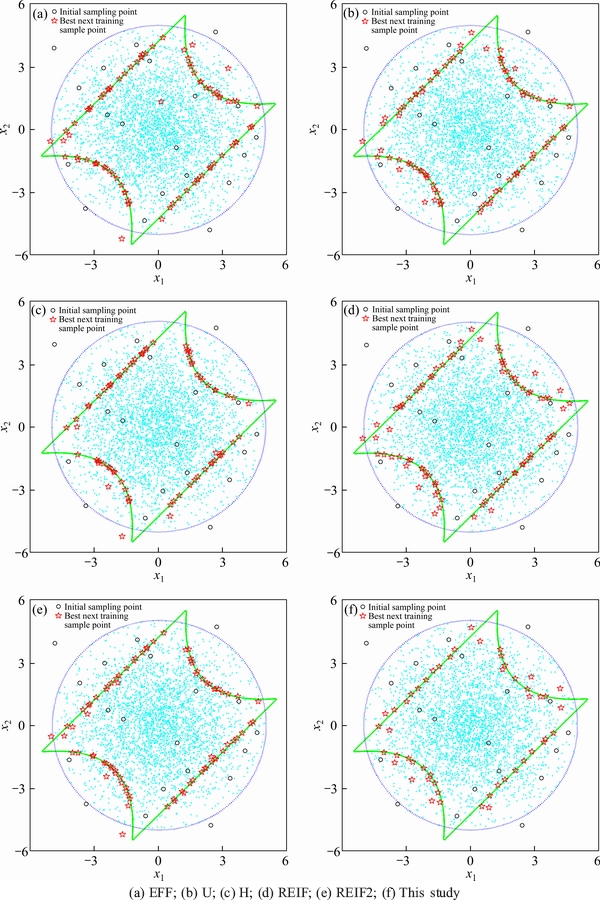
Figure 5 Sampling results of different methods in numerical case I:
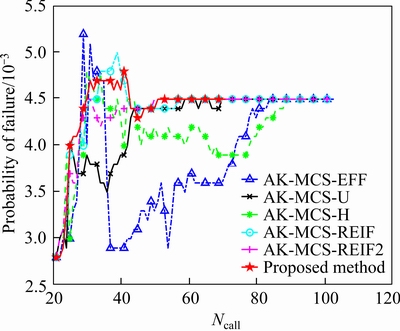
Figure 6 History evaluation of Pf corresponding to Ncall for different methods
Compared with the benchmark result determined by the crude MCS method using 106 samples, all the AK-MCS methods use fewer simulations and yield accurate results. It can be seen from Table 1, the average number of Ncall for the developed approach and other AK-MCS methods (including EFF, U, H, REIF, REIF2) are 70.0, 102.5, 99.1, 90.0, 110.2 and 94.8, respectively. The COV and estimated maximum error rate (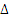
Figure 7 CPU-time for different methods
5.2 Numerical case II
The second case is a reliability issue consisting of a non-linear single-degree-of-freedom system (as shown in Figure 8). This case has been investigated in Ref. [24], and its performance function is defined below:
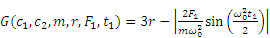
where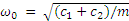 
Table 2 Probabilistic characteristics of input variables in numerical case II
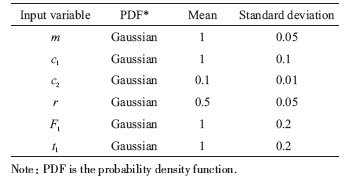
Table 3 Reliability analysis results of different methods in numerical case II
Figure 8 Dynamic response of non-linear oscillator
5.3 Engineering example I: a steel frame structure
Reliability analysis of a two-bay six-story steel frame structure is studied to further investigate the performance of the developed approach. The steel frame structure is depicted in Figure 9(a). As shown in Figure 9(a), the height and the width of the steel frame structure are (3×6) m and (7.5×2) m, respectively. Column and beam of the steel frame structure are modeled by using BEAM188 element in ANSYS software. The cross-section of column and beam members are I-shape and box, respectively, as shown in Figure 9(b).
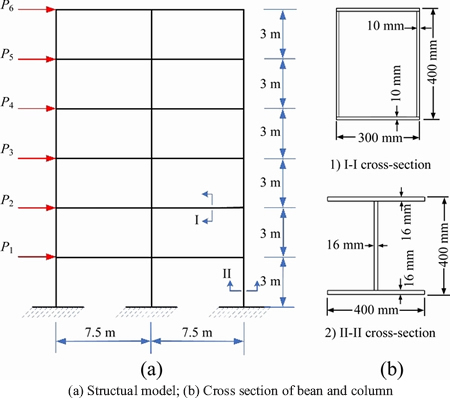
Figure 9 Two-bay six-story steel frame structure:
Displacement is an important indicator of the structural serviceability limit state. Therefore, the implicit performance function of this case is presented based on the maximal horizontal deformation Dmax, as follows:
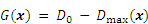
where the maximal horizontal deformation Dmax is solved by finite element analysis, as illustrated in Figure 10, and D0=22.5 is a preset threshold.
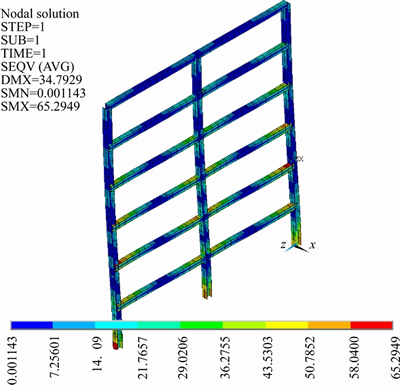
Figure 10 Finite element model of steel frame structure
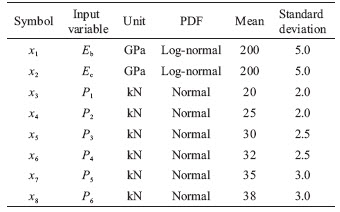
The elasticity modulus Ec, Eb (subscripts c and b represent column and beam, respectively), and the external lateral loads Pi (i=1, 2, …, 6) can influence the performance function of the steel frame structure. Therefore, the Ec, Eb and Pi (i=1, 2, …, 6) are chosen as the input variables. Table 4 present the probabilistic characteristics of each input variable.
Table 4 Probabilistic characteristics of input variables in the engineering example I
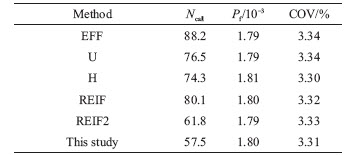
In the beginning, 50 sampling points are generated by LHS. Subsequently, the new sampling point is identified to construct the more precise Kriging model. Then, the reliability analysis results can be acquired through the various AK-MCS methods. Table 5 summarizes the reliability analysis results when the threshold parameter of the performance function is D0=22.5. The Ncall required by the developed approach is much less than other AK-MCS methods. Therefore, this method is feasible and can be applied to practical engineering problems, especially for those problems with time-consuming calculations.
Table 5 Reliability analysis results of different methods in engineering example I
In summarize, the merits of the developed approach are demonstrated according to the study results of the two numerical cases and an engineering case. Compared with other AK-MCS methods, the developed approach not only decreases the Ncall but also decreases the training times about the active learning function. Therefore, the developed approach is feasible and more excellent than other AK-MCS methods (including EFF, U, H, REIF, REIF2). Furthermore, the developed approach is capable of being further improved by being integrated with variance reduction techniques (e.g., importance sampling and subset simulation) to reduce the Ncall and computation-related cost in depth.
6 Conclusions
The present study attempts to raise the efficiency of the AK-MCS algorithm in reliability analysis. A novel adaptive sampling approach receives the development based on an innovative active learning function JSD and the trust-region method, which can efficiently estimate the failure probability. The developed approach shows high accuracy and efficiency in three case studies. The following conclusions are drawn:
1) An innovative active learning function integrated with JSD is developed for selecting the most suitable sampling points. The JSD based on information theory benefits from boundedness and symmetry. It is applied as a utility function to measure the difference of probability distributions predicted by the Kriging model. It can guarantee not only the selected sampling points approach to the area of limit state boundary, but also have large discreteness. Therefore, the active learning function JSD can update the Kriging model in an effective manner. Furthermore, the active learning function JSD is able to be employed not only in combination with the MCS but also in many reliability methods (e.g., importance sampling, and subset simulation).
2) A trust-region method is developed for reducing the candidate sampling pool size inside the evaluation procedure of active learning function. It can improve the computation efficiency for the evaluation of active learning function without compromising the estimated accuracy of the failure probability. Besides, the termination criterion based on the uncertainty function is introduced as the condition of convergence of the active learning function JSD. This termination criterion is effective for the active learning function JSD and more robust corresponding to the failure probability of different situations.
Appendix
For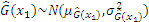
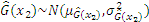
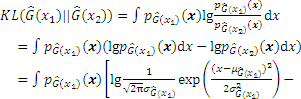
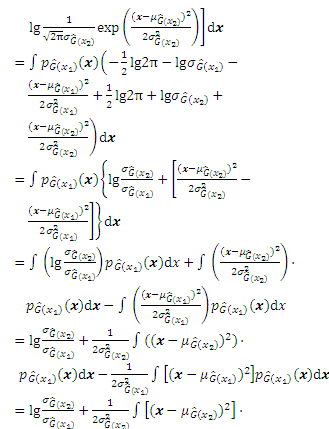
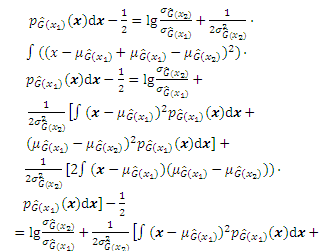
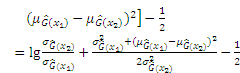
According to the definition, the JSD can be derived through the KL divergence:
Substituting Eq. (A-1) into Eq. (A-2), the JSD can be obtained as follows:
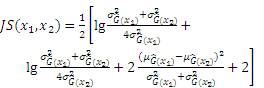
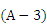
Therefore, the novel active learning function JSD can be derived as follows:
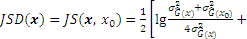
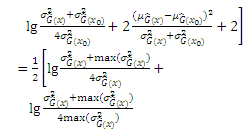
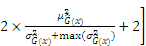
where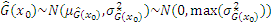 
Contributors
The overarching research goals were developed by CHEN Liang-jun, HONG Yu, and GOU Hong-ye. CHEN Liang-jun and HONG Yu established the models and calculated the failure probability. CHEN Liang-jun, GOU Hong-ye, and PU Qian-hui analyzed the calculated results. The initial draft of the manuscript was written by CHEN Liang-jun, HONG Yu, and SUJITH M. All authors replied to reviewers' comments and revised the final version.
Conflict of interest
CHEN Liang-jun, HONG Yu, SUJITH M, GOU Hong-ye, and PU Qian-hui declare that they have no conflict of interest.
References
[1] HU Wei-fei, CHOI K K, CHO H. Reliability-based design optimization of wind turbine blades for fatigue life under dynamic wind load uncertainty [J]. Structural and Multidisciplinary Optimization, 2016, 54(4): 953-970. DOI: 10.1007/s00158-016-1462-x.
[2] LIU Wang-sheng, CHEUNG S H. Reliability based design optimization with approximate failure probability function in partitioned design space [J]. Reliability Engineering & System Safety, 2017, 167: 602-611. DOI: 10.1016/j.ress. 2017.07.007.
[3] JIANG Chen, QIU Hao-bo, YANG Zan, CHEN Li-ming, GAO Liang, LI Pei-gen. A general failure-pursuing sampling framework for surrogate-based reliability analysis [J]. Reliability Engineering & System Safety, 2019, 183: 47-59. DOI: 10.1016/j.ress.2018.11.002.
[4] ZHANG Z, JIANG C, WANG G G, HAN X. First and second order approximate reliability analysis methods using evidence theory [J]. Reliability Engineering & System Safety, 2015, 137: 40-49. DOI: 10.1016/j.ress.2014.12.011.
[5] TORII A J, LOPEZ R H, MIGUEL L F F. A second order SAP algorithm for risk and reliability based design optimization [J]. Reliability Engineering & System Safety, 2019, 190: 106499. DOI: 10.1016/j.ress.2019.106499.
[6] ZHANG Jun-fu, DU Xiao-ping. A second-order reliability method with first-order efficiency [J]. Journal of Mechanical Design, 2010, 132(10): 101006. DOI: 10.1115/1.4002459.
[7] LING Chun-yan, LU Zhen-zhou, SUN Bo, WANG Min-jie. An efficient method combining active learning Kriging and Monte Carlo simulation for profust failure probability [J]. Fuzzy Sets and Systems, 2020, 387: 89-107. DOI: 10.1016/j.fss.2019.02.003.
[8] ALBAN A, DARJI H A, IMAMURA A, NAKAYAMA M K. Efficient Monte Carlo methods for estimating failure probabilities [J]. Reliability Engineering & System Safety, 2017, 165: 376-394. DOI: 10.1016/j.ress.2017.04.001.
[9] ABDOLLAHI A, AZHDARY MOGHADDAM M, HASHEMI MONFARED S A, RASHKI M, LI Y. A refined subset simulation for the reliability analysis using the subset control variate [J]. Structural Safety, 2020, 87: 102002. DOI: 10.1016/j.strusafe.2020.102002.
[10] MOAREFZADEH M R, SUDRET B. Implementation of directional simulation to estimate outcrossing rates in time-variant reliability analysis of structures [J]. Quality and Reliability Engineering International, 2018, 34(8): 1818-1827. DOI: 10.1002/qre.2374.
[11] PAPAIOANNOU I, STRAUB D. Combination line sampling for structural reliability analysis [J]. Structural Safety, 2021, 88: 102025. DOI: 10.1016/j.strusafe.2020.102025.
[12] XIAO Ning-cong, ZHAN Hong-you, YUAN Kai. A new reliability method for small failure probability problems by combining the adaptive importance sampling and surrogate models [J]. Computer Methods in Applied Mechanics and Engineering, 2020, 372: 113336. DOI: 10.1016/j.cma. 2020.113336.
[13] BHOSEKAR A, IERAPETRITOU M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review [J]. Computers & Chemical Engineering, 2018, 108: 250-267. DOI: 10.1016/j.compchemeng.2017.09.017.
[14] KABASI S, ROY A, CHAKRABORTY S. A generalized moving least square-based response surface method for efficient reliability analysis of structure [J]. Structural and Multidisciplinary Optimization, 2021, 63(3): 1085-1097. DOI: 10.1007/s00158-020-02743-9.
[15] LI Tian-zheng, DIAS D. Tunnel face reliability analysis using active learning Kriging model—Case of a two-layer soils [J]. Journal of Central South University, 2019, 26(7): 1735-1746. DOI: 10.1007/s11771-019-4129-0.
[16] TAO Tao, ZIO E, ZHAO Wei. A novel support vector regression method for online reliability prediction under multi-state varying operating conditions [J]. Reliability Engineering & System Safety, 2018, 177: 35-49. DOI: 10. 1016/j.ress.2018.04.027.
[17] YOON S, LEE Y J, JUNG H J. Accelerated Monte Carlo analysis of flow-based system reliability through artificial neural network-based surrogate models [J]. Smart Structures and Systems, 2020, 26(2): 175-184. DOI: 10.12989/sss. 2020.26.2.175.
[18] WANG Qi-qi, MOIN P, IACCARINO G. A high order multivariate approximation scheme for scattered data sets [J]. Journal of Computational Physics, 2010, 229(18): 6343-6361. DOI: 10.1016/j.jcp.2010.04.047.
[19] BICHON B J, ELDRED M S, SWILER L P, MAHADEVAN S, MCFARLAND J M. Efficient global reliability analysis for nonlinear implicit performance functions [J]. AIAA Journal, 2008, 46(10): 2459-2468. DOI: 10.2514/1.34321.
[20] ECHARD B, GAYTON N, LEMAIRE M. AK-MCS: An active learning reliability method combining Kriging and Monte Carlo Simulation [J]. Structural Safety, 2011, 33(2): 145-154. DOI: 10.1016/j.strusafe.2011.01.002.
[21] LU Z, LU Zhen-zhou, WANG Pan. A new learning function for Kriging and its applications to solve reliability problems in engineering [J]. Computers & Mathematics With Applications, 2015, 70(5): 1182-1197. DOI: 10.1016/j.camwa.2015.07.004.
[22] YANG Xu-feng, LIU Yong-shou, ZHANG Yi-shang, YUE Zhu-feng. Probability and convex set hybrid reliability analysis based on active learning Kriging model [J]. Applied Mathematical Modelling, 2015, 39(14): 3954-3971. DOI: 10.1016/j.apm.2014.12.012.
[23] SUN Zhi-li, WANG Jian, LI Rui, TONG Cao. LIF: A new Kriging based learning function and its application to structural reliability analysis [J]. Reliability Engineering & System Safety, 2017, 157: 152-165. DOI: 10.1016/j.ress. 2016.09.003.
[24] ZHANG Xu-fang, WANG Lei, SORENSEN J D. REIF: A novel active-learning function toward adaptive Kriging surrogate models for structural reliability analysis [J]. Reliability Engineering & System Safety, 2019, 185: 440-454. DOI: 10.1016/j.ress.2019.01.014.
[25] YUN Wan-ying, LU Zhen-zhou, JIANG Xian, ZHANG Lei-gang, HE Peng-fei. AK-ARBIS: An improved AK-MCS based on the adaptive radial-based importance sampling for small failure probability [J]. Structural Safety, 2020, 82: 101891. DOI: 10.1016/j.strusafe.2019.101891.
[26] WEN Zhi-xun, PEI Hai-qing, LIU Hai, YUE Zhu-feng. A sequential Kriging reliability analysis method with characteristics of adaptive sampling regions and parallelizability [J]. Reliability Engineering & System Safety, 2016, 153: 170-179. DOI: 10.1016/j.ress.2016.05.002.
[27] WANG Ze-yu, SHAFIEEZADEH A. REAK: Reliability analysis through error rate-based adaptive Kriging [J]. Reliability Engineering & System Safety, 2019, 182: 33-45. DOI: 10.1016/j.ress.2018.10.004.
[28] HU Zhen, MAHADEVAN S. A single-loop kriging surrogate modeling for time-dependent reliability analysis [J]. Journal of Mechanical Design, 2016, 138(6): 061406. DOI: 10.1115/1.4033428.
[29] XIAO Fu-yuan. Multi-sensor data fusion based on the belief divergence measure of evidences and the belief entropy [J]. Information Fusion, 2019, 46: 23-32. DOI: 10.1016/j.inffus. 2018.04.003.
[30] van ERVEN T, HARREMOS P. Rényi divergence and kullback-leibler divergence [J]. IEEE Transactions on Information Theory, 2014, 60(7): 3797-3820. DOI: 10.1109/TIT.2014.2320500.
[31] HAN Zhong-hua. Kriging surrogate model and its application to design optimization: A review of recent progress [J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese)
[32] LIN J. Divergence measures based on the Shannon entropy [J]. IEEE Transactions on Information Theory, 1991, 37(1): 145-151. DOI: 10.1109/18.61115.
[33] SHI Yan, LU Zhen-zhou, HE Ru-yang, ZHOU Yi-cheng, CHEN Si-yu. A novel learning function based on Kriging for reliability analysis [J]. Reliability Engineering & System Safety, 2020, 198: 106857. DOI: 10.1016/j.ress.2020.106857.
(Edited by ZHENG Yu-tong)
中文导读
基于Jensen-Shannon散度的自适应采样方法的高效可靠性分析
摘要：目前，对基于代理模型的可靠度分析进行了广泛的研究，该方法在保证评估准确性的同时，减少调用真实且复杂性能函数的次数。为了更高效地评估失效概率，本文提出了一种自适应采样方法。首先，结合Jensen-Shannon散度(JSD)推导了一种新的主动学习函数，通过选择最合适的采样点更新Kriging模型。为了提高效率，建立了一种信念域方法，用以减少有关主动学习功能函数评估时的计算负担，同时不影响评估的准确性。此外，引入了基于不确定性函数的终止准则，以确保在不同的失效概率情况下实现更好的鲁棒性。该方法主要有以下两个优点：新选择的采样点接近极限状态边界区域，且这些采样点具有较大的离散性。最后，通过三个案例分析验证了方法的可行性和性能。结果表明，与蒙特卡罗模拟或其他主动学习函数相比，该方法在处理复杂问题时在效率、收敛性和准确性方面均具有优势。
关键词：可靠度；蒙托卡洛；Kriging模型；Jensen-Shannon熵；信念域
Foundation item: Project(KY201801005) supported by the China-Indonesia High-Speed Rail Technology Joint Research Center
Received date: 2021-01-06; Accepted date: 2021-04-25
Corresponding author: HONG Yu, PhD, Engineer; Tel: +86-15208102858; E-mail: hongyu@swjtu.edu.cn; ORCID: https://orcid.org/ 0000-0002-6117-9281
Abstract: Extensive studies have been carried out for reliability studies on the basis of the surrogate model, which has the advantage of guaranteeing evaluation accuracy while minimizing the need of calling the real yet complicated performance function. Here, one novel adaptive sampling approach is developed for efficiently estimating the failure probability. First, one innovative active learning function integrating with Jensen-Shannon divergence (JSD) is derived to update the Kriging model by selecting the most suitable sampling point. For improving the efficient property, one trust-region method receives the development for reducing computational burden about the evaluation of active learning function without compromising the accuracy. Furthermore, a termination criterion based on uncertainty function is introduced to achieve better robustness in different situations of failure probability. The developed approach shows two main merits: the newly selected sampling points approach to the area of limit state boundary, and these sampling points have large discreteness. Finally, three case analyses receive the conduction for demonstrating the developed approach’s feasibility and performance. Compared with Monte Carlo simulation or other active learning functions, the developed approach has advantages in terms of efficiency, convergence, and accurate when dealing with complex problems.
