Numerical simulation in powder compaction of metallurgy component

HUANG Chun-man(黄春曼), CHEN Pu-qing(陈普庆), SHAO Ming(邵 明), LI Yuan-yuan(李元元)

College of Mechanical Engineering, South China University of Technology, Guangzhou 510640, China

Received 28 February 2006; accepted 15 May 2006

Abstract:

Some flow stress models was used to simulate the compaction of a cylindrical specimen. A new flow stress model was presented by analyzing and summarizing the powder compact experiment with different initial densities. Compared with other models, the new model fits better with the experiments. The compaction process of a synchronizer hub was simulated with new model and the synchronizer hub shape was improved by the simulation results. The density distribution was measured and compared with the simulation results of splitting the samples into pieces. The comparison shows that the model could be used to simulate the powder compact process in an efficient and accurate manner. And the results indicate that the density distribution is homogenous after optimization.

Key words:

powder compaction; design distribution; numerical simulation;

Forming multi-level component in die compaction, the density is more or less inhomogeneous depending on the part geometry, the tool design and the friction between powder and die wall[1-3]. The product distortions are result of inhomogeneous density distribution in the green part, and inhomogeneous density distribution influences the strength and dimensional accuracy. Metallurgy component shape, tools and compact process, the conventional method of trial and error is often a time-consuming process. To reduce design time and costs, the whole compact process can be optimized by numerical simulations.

During cold compact process, metal powder is often considered a kind of time-independent, elasto-plastic and compressible material[4,5]. KUHN et al[6], GREEN et al[7], SHIMA et al[8] and DORAIVELU et al[9] postulated different yield function characterized with an ellipsoidal yield surface. And the Drucker-Prager-Cap yield surface was presented by Drucker and Prager based on soil mechanical theory[10]. Kraft simulated cutting insert and optimized upper punch and lower punch with Drucker-Prager-Cap model[11]. Some kinds of discreet models have also been presented and applied in the simulation, while the large computation capability they
require still hinders the application in industry[12,13]. In this paper, a new flow stress model was presented, and the model was applied in optimizing synchronic the hub component.

 Proposed ellipsoidal yield criteria of porous material which can be generalized as

                          (1)

                                  (2)

where  F is the yield function,  and J₁ are the second invariant of deviatoric stress tensor and the first invariant of stress tensor, respectively. Y_R is the yield stress of porous material; Y₀ is the yield stress of non-porous material. A, B and δ are functions of relative density. KUHN, DORAIVELU and LEE noticed that

A=2(1+v)                                   (3)

                                  (4)

where  v is material Poisson’s ratio. An experiential relationship between v and ρ has been proposed by ZHDANOVICH[14]. It was assumed that

v=0.5ρⁿ                                     (5)

KUHN et al[6], DORAIVELU et al[9] and LEE et al[15] assumed n=2 in their yield criterion. Flow stress δ is also a function of ρ, which should be determined on experimental results. KUHN, DORAIVELU and LEE had different assumptions on flow stress function. The relationship between δ and ρ are listed in Table 1.

Table 1 Different assumptions of δ(ρ)

CHEN[16] derived a general elasto-plastic matrix based ellipsoidal yield criteria applied for powder material as

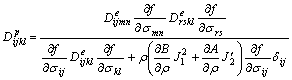(6)

where

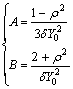                                (7)

where   is the plastic matrix; f is the yield function;  is the yield stress of the non-porous material, δ is function of ρ, which should be determined by the experimental results.

The above model was used to develop a user subroutines of MSC.Marc.

The above elasto-plastic model and different assumptions of δ were implemented into user subroutines of MSC.Marc to simulate the compact process. In simulation, the diameter of cylindrical specimen is 12 mm, and the height is 20 mm. Model parameters were set as σ_s=205 MPa, elastic module was E=210ρ MPa and Poisson’s ratio was v=0.5ρ². The initial relative density was 0.45. Since loose powder is quite easy to deform, the value of ρ_c should be very close to the initial relative density, it was set at 0.449 9. The upper punch, lower punch and die were assumed as rigid bodies in simulation. The friction coefficient on die walls was assumed to be 0.2[17].

Uniaxial compaction experiments were carried out on test machine SANS-CMT5105. Ferrous powder with 0.2% carbon was filled in a cylindrical die of 12 mm in diameter and the filling height was 20 mm. During the compact process, curves of load vs displacement for upper punch were recorded by testing system. Load on the upper punch increased from 0 to 75 kN.

The displacement vs load curves obtained from both experiments and simulation are compared in Fig.1. It shows that the simulation curves of Kuhn model, Doraivelu model and Lee model do not exactly fit with the experimental curve.

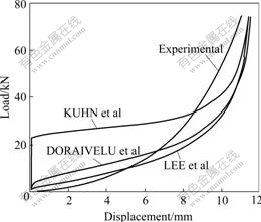
Fig.1 Load vs displacement curves obtained of upper punch

A number of powder compaction experiments with different initial densities were carried out to obtain load vs displacement curves. From the comparison between the simulation and the experiment, and considering dimension analysis about δ(ρ) by Doraivelu, a new proposed of flow stress was obtained as

                            (8)

The curve simulated with the new model is compared with experimental curve in Fig.2. It shows that the new flow stress model fits better with the experimental results.

A synchronizer hub used in the automotive industry is shown in Fig.3. The synchronizer hub has three upper levels steps and three lower levels steps. It requires high dimensional accuracy and high strength. For the purpose to guarantee strength and dimensional accuracy of the product, homogeneous density distribution is required. Fig.4 shows the schematic illustration of the die, punches and powder of synchronizer hub compaction. The synchronizer hub is non-axisymmetric complex 3D

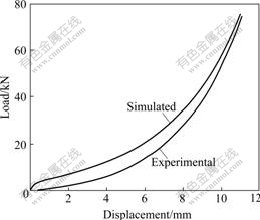
Fig.2 Comparison of curves simulated with new model experimental curve

Fig.3 Schematic diagram of synchronizer hub (mm)

component. It was pressed by five punches, a core rod, and the die. The upper inner step and upper middle step are formed by one punch. The main compact process is shown in Fig.5, the filling height of outer section, middle section and inner section are 36 mm, 27 mm and 9 mm, respectively. In compacting phase, the lower inner punch is fixed and the other punches move to the compaction position at the same time, the core rod and the die move floatable.

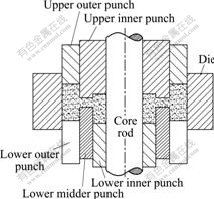
Fig.4 Schematic illusion of die, punches and powder

The simulation uses MSC.Marc user subroutines with the new flow stress model presented above. In the simulation, the synchronizer hub was modeled by 3D structured meshed in totally 11 739 four-node tetrahedral elements and 3 085 nodes. The lower inner punch is fixed and the other punches are moved to their final positions as a linear function of time. The time to reach the final positions is assumed to be 1 s. The calculation was divided into 50 incremental steps. Fig.6 shows the relative density distributions obtained in the first simulations. The highest relative density is 0.987 6, and the lowest relative density is 0.45, the density distribution is very inhomogeneous. For the inner flange of synchronizer hub is right angle, the powder is hardly compressed at that position. In order to obtain more homogeneous density distribution, the right angle is modified to 60?(Fig.7).

The density distribution after improvement is shown in Fig.8. The highest relative density is 0.849 2 which lies in the rim of top, and the lowest relative density is 0.753 5 which lies in the flange of inner. This shows that as the effect of die-wall friction, the upper half of outer section is more densified than the lower half of outer section. The largest gradients develop in corners where powder movements are restrained by the friction of die walls. The relative density of the inner and middle section are lower than that of outer section, for the inner and middle sections are pressed by the same punch, and

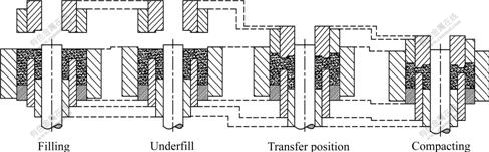
Fig.5 Schematic diagram of main compact process

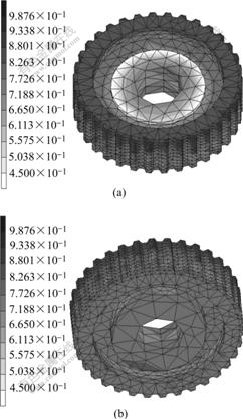
Fig.6 Relative density distribution of first simulation: (a) Top;  (b) Bottom

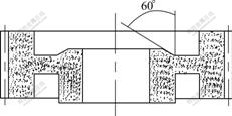
Fig.7 Improved structure of synchronizer hub: (a) Top; (b) Bottom

A press with five independent punches, a core rod, and the die was used to compact the synchronizer hub. The density distribution was experimentally measured by cutting out one 34th of the synchronizer hub and divide into eleven sections. Fig.9 shows the density distribution of the measurements compared with that of simulation, it shows that the simulated results agree well with the experimental ones.

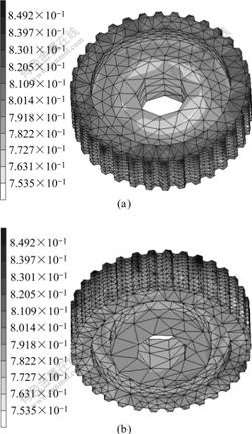
Fig.8 Relative density distribution of simulation after improvement: (a) Top; (b) Bottom

Fig.9 Metrical density distribution compared with simulation

5 Conclusions

1) Different flow stress models were used to simulate the compact process of a cylindrical specimen modeled in 3D geometry. Load vs displacement curves simulated with KUHN model, DORAIVELU model and LEE model were compared with experimental ones. A new flow stress model was presented from comparison between the simulation and experiment, and considering dimension analysis about δ(ρ) by Doraivelu. The result shows that the new model fits better than other models.

2) The new flow stress model was used to simulate and improve a synchronizer hub, the relative density distributions of synchronizer hub was obtained by improved simulation. The improved synchronizer hub was compacted and cut out to measure the density. The results show that the synchronic hub obtains more homogeneous density distribution after improvement, and the new model can reliably predict the green density distribution. Simulating powder compaction is capable of improving powder metallurgy component in an efficient and accurate manner.

3) The more ambitious goal is to predict tool deformations and stresses, optimize the tools and press kinematics by the computer simulation, before the tool is manufactured and tested, and prevent the crack in green parts.

References

[1] HUANG Pei-yun. Powder Metallurgical Theory [M]. Beijing: Metallurgical Indrstry Publishing Press, 1997. (in Chinese)

[2] LI Yuan-yuan, ZHANG Da-tong, XIAO Zhi-yu, NGAI Tung-wai. Influence of high-energy ball milling on Al-30wt%Si powder and ceramic particulate [J]. Trans Nonferrous Met Soc China, 2000(3): 324-327.

[3] LI Yuan-yuan, ZHANG Da-tong, NGAI Tung-wai, XIA Wei, LONG Yan. Diffusion couple between a high-strength wear-resisting aluminum bronze and machining tools materials [J]. Trans Nonferrous Met Soc China, 1999, 9(1): 6-10.

[4] STORAKERS B, FLECK N A, MCMEEKING R M. The viscoplastic compaction of composite powders [J]. Journal of Mechanics and Physics of Solids, 1999, 47: 785-815.

[5] REDANZ P. Numerical modeling of the powder compaction of a cup [J]. European Journal of Mechanics A/Solids, 1999, 18: 399-413.

[6] KUHN H A, DOWNEY C L. Deformation characteristics and plasticity theory of sintered powder materials [J]. International Journal of Powder Metallurgy, 1971, 7(1): 15-25.

[7] GREEN R J. A plasticity theory for porous solids [J]. International Journal of Mechanics Science, 1972, 14: 215-224.

[8] SHIMA S, OYANE M. Plasticity theory for porous metallurgy [J]. International Journal of Mechanical Sciences, 1976, 18(6): 285-291.

[9] DORAIVELU S M, GEGEL H L, GUNASEKERA J S. A new yield function for compressible P/M materials [J]. International Journal of Mechanical Sciences, 1984, 26: 527-535.

[10] DRUCKER D C, GIBSON R E, HENKEL D J. Soil mechanics and workhardening theories of plasticity [J]. Trans ASCE, 1953, 122: 338-346.

[11] KRAFT T. Optimizing press tool shapes by numerical simulation of compaction and sintering—application to a hard metal cutting insert [J]. Modelling and Simulation in Materials Science and Engineering, 2003(11): 381-400.

[12] CHEN Pu-qing, XIA Wei, ZHOU Zhao-yao, ZHU Quan-li, LI Yuan-yuan. Three-dimensional combined finite-discrete element approach for simulation of the single layer powder compaction process [J]. Trans Nonferrous Met Soc China, 2004(14): 751-755.

[13] MARTI C L, BOUVARD D. Study of the cold compaction of composite powders by the discrete element method [J]. Acta Materialia, 2003(51): 373-386.

[14] ZHDANOVICH G M. Theory of Compacting of Metal Powders [M]. Translated from Teorizc Pressovaniya Metzllichaskikli Poroshkov, 1969, by the Foreign Technology Division, Ohio: Wright-Patterson Air Force Base, 1969.

[15] KIM H S, LEE D N. Power-law creep model for densification of powder compacts [J]. Mater Sci Eng A, 1999, A271: 424-429.

[16] CHEN Pu-qing. Mechanical Modeling and Numerical simulation of Metal Powder Compact Process [D]. Guangzhou: South China University of Technology. 2004. (in Chinese)

[17] NGAI T L, CHEN W P, XIAO Z Y. Die wall lubricated warm compaction of iron-based powder metallurgy material [J]. Trans Nonferrous Met Soc China, 2002, 12(6): 1095-1098.

(Edited by LONG Huai-zhong)

Foundation item: Projects(50325516, 50135020) supported by the National Natural Science Foundation of China; Project(003019) supported by the Natural Science Foundation of Guangdong Province, China

Corresponding author: HUANG Chun-man; Tel: +86-20-87112933; E-mail: mysterstar@163.com