- Abstract:
- 1 Introduction▲
- 2 Derivation of effe...▲
- 3 Conclusions▲
- References
- Figure
- Fig.1 Each phase and its stress in section of point of saturated soil
- Fig.2 Each phase and its stress in section of point of nearly- saturated soil
- Fig.3 Radius of bubble cut and surface tension
- Fig.4 Sketch map of bubble adhered to surface of soil granule
- Fig.5 Each phase and its stress in section of point of soil when being surrounded by water
- Fig.6 Each phase and its stress in section of point of soil when being surrounded by air
J. Cent. South Univ. Technol. (2011) 18: 2137-2142
DOI: 10.1007/s11771-011-0954-5![]()
Effective stress in soils under different saturation conditions
XU Hao-feng(徐浩峰)1, 2, XIE Kang-he(谢康和)1
1. Key Laboratory of Soft Soils and Geoenvironmental Engineering of Ministry of Education,Zhejiang University, Hangzhou 310027, China;
2. Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract:
BISHOP’s effective stress or two state stress variables are unsatisfactory for unsaturated soils where one of fluid phases is discontinuous, so new expressions of effective stress should be founded. The approach for derivation was according to the principle of equilibrium of forces (i.e., the stress-sharing principle), and it was firstly validated by demonstrating TERZAGHI’s principle of effective stress. And then, the derivations were subdivided into four parts according to different pore air states: 1) air bubbles were spherical and suspended in pore water; 2) air bubbles were bound on soil skeleton; 3) air bubbles held almost the single section of pore; 4) air phase was continuous. The different formulae of effective stress were presented. Conclusions are drawn as follows: 1) For nearly-saturated soils, the “real” effective stress would be a little smaller than TERZAGHI’s effective stress; 2) For soils in which air phase is discontinuous in the form of bubbles, a new concept of pore air elastic pressure is put forward, and the total stress can be constituted by effective stress, pore water pressure and pore air elastic pressure; 3) For soils in which air phase is continuous, effective stress is equal to the value of the total stress plus suction; 4) Suction can be divided into two parts: one is the effect caused by additional pressure, and the other is the contract action by the “skin”.
Key words:
unsaturated soils; effective stress; suction; surface tension; occluded gas; saturation;
1 Introduction
The principle of effective stress is very important in the discipline of soil mechanics, but it remains vague for unsaturated soils, even for saturated soils. Although TERZAGHI’s principle of effective stress has been extensively acknowledged and used, the effective stress of saturated soil was usually regarded as the “inter- particle forces” [1]. And in order to get a mathematical confirmation for the principle, the wave-shaped plane was often used to traverse the interface of soil grains, so that the area of solid in the plane was the smallest [2]. This approach can be understood and accepted to sandy soils, but the explanation for clay is unacceptable. SHEN [3] opposed the introduction of the concept of inter- granular stress into the discipline of soil mechanics.
For nearly saturated soils, TERZAGHI’s principle of effective stress is commonly used without being testified. How extent would the bubbles of gas act on the principle? Some researchers [4-5] regarded water and air as mixture fluid, while the values of pore mixture fluid pressure were often different among these literatures. Some researchers substituted the terminology of effective stress by “operative stress”; however, its expression was wholly the same to the effective stress [6].
For unsaturated soils, there are two types of stress framework [7]: one is single stress framework, e.g., BISHOP single effective stress; the other is two independent stress state variables framework, e.g., FREDLUND independent stress variables.
BISHOP [8] had derived the formula of effective stress according to the equilibrium of forces for every phase in soil. Subsequently, the parameter of effective stress was tested by many researchers [9]. However, in BISHOP’s derivation, he had ignored the effect of surface tension on the interface between water and air [10]. The air/water interface was also called as the contractile skin or the surface film. It was regarded as a fourth independent phase by FREDLUND [11]. The contractile skin is known to play a dominant role in unsaturated soil. It is acknowledged widely that the surface tension should not be neglected when attempting to found the effective stress equation for unsaturated soils.
Besides the approach that was used by BISHOP of establishing the effective stress, there was another usual approach according to the principle of deformation equivalence [12-14]. However, when CHEN et al [13] derived the formula, they provided the premise that air phase and water phase were both continuous in the soil.
The above premise was also adapted to two independent stress state variables framework [7] (suction Su=ua-uw and net normal stress σ-ua, or suction Su=ua-uw and net normal stress σ-uw). When air bubbles were embedded in liquid phase, i.e., air phase was discontinuous and water phase was continuous, the pressures of air in the bubbles were not measurable [15]. When water was discontinuous and air phase was continuous, the equal pressure of water would not exist and the average pressure of water would not be defined easily.
Previous studies can only be applicable to soils where both the water and the air are continuous [16], e.g. LU et al’s equation [17]. Thus, to soils where either the water or the air is discontinuous, these previous results are unsatisfactory.
In this work, the formulae of effective stress were derived under the stress-sharing principle. Firstly, the approach was used and validated by demonstrating TERZAGHI’s effective stress. And then, considering the different saturated conditions of soils, derivations were subdivided into four stages: 1) air bubbles were spherical and suspended in pore water; 2) air bubbles were bound on soil skeleton; 3) with degree of saturation decreasing, air bubbles held almost the single section of pore; 4) air phase was continuous.
2 Derivation of effective stress
2.1 Demonstration of TERZAGHI’s formula of effective stress
A point in the earth was picked, and a plane where one primary stress acted was got. And the area of plane was postulated as A. For saturated soils, the plane contained only soil grains and water. Assuming the area of grains to be As,i, the stress acted on grains to be σs,i, the area of pore water to be Aw, and the pressure of pore water to be uw, each phase and its stress were shown in Fig.1. The equation could be gotten as
![]()
![]() (1)
(1)
Because ∑As,i+Aw=A, the above equation became
![]() (2)
(2)
Defining the effective stress σ′ to be
![]() (3)
(3)
Then, Eq.(2) was transformed to be
![]() (4)
(4)
Equation (4) is TERZAGHI’s formula of effective stress exactly.
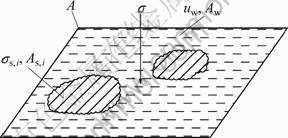
Fig.1 Each phase and its stress in section of point of saturated soil
Through the derivation, we can conclude: 1) the effective stress is not the stress acting on the interface between grains, but the average value to the whole area. The effective stress is not a real stress. 2) The ratio of grain area in the whole plane would not influence the validity of the principle. 3) There is a postulation that the soil grains are incompressible. Otherwise, the pressure of pore water uw should not be subtracted in Eq.(3).
2.2 Effective stress in nearly saturated soils
For nearly saturated soils, the air phase was discontinuous in the form of bubbles entrapped in the water phase. According to BARDEN [18], when the saturation degree of soil was more than 95%, mostly air bubbles were bound on the soil skeleton, and the number of air bubbles that flowed with pore water was very few. Now, we considered this problem to be analyzed in two steps. Firstly, air bubbles were all suspended in pore water; secondly, air bubbles were bound on the soil skeleton.
1) Spherical air bubbles suspended in pore water [5]
Assuming the number of air bubbles in the plane to be n, the spherical radius of one bubble intercepted to be Ri, the area intercepted of one bubble to be Aa,i, circular radius to be ri, air pressure in the bubble to be ua,i, and the coefficient of surface tension to be T, from Fig.2, we could get
![]() (5)
(5)
where la,i was the length of circumference of air bubble i, la,i=2riπ; θ was the tilt angle between the direction of surface tension T and the plane, as shown in Fig.3.
From Fig.3, we could get ri=Risinθi. And according to Laplace’s formula, we got the following equation:
![]() (6)
(6)
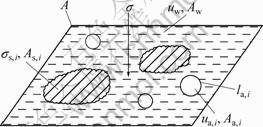
Fig.2 Each phase and its stress in section of point of nearly- saturated soil
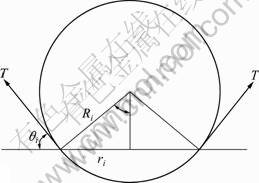
Fig.3 Radius of bubble cut and surface tension
And we derived the equation:
![]()
![]()
![]() (7)
(7)
Inserting the above equation in Eq.(5), the equation gotten is not different to Eq.(2). So, air bubble suspended in pore water does not influence the principle. TERZAGHI’s principle of effective stress is still applicable.
2) Air bubbles bound on soil skeleton
If air bubbles adhered on the soil grains, the bubble would not be an intact sphere and the plane cut would not be a regular circle. The shape was postulated, and the smallest ex-circle was drawn containing the bubble. As shown in Fig.4, Aa was the area intercepted of one bubble, Aa1 was the area of part of ex-circle that was in soil grains, Aa2 was the area of part of ex-circle that was out of soil grains minus the real area of the bubble, l1 was the length of circular arc overlapping the bubble, l2 was the length of circular arc in the water, l3 was the length of circular arc in the soil grains, and l4 was the length of curve-part of the bubble which was not matched by the circle.
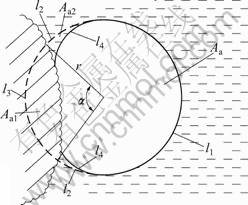
Fig.4 Sketch map of bubble adhered to surface of soil granule
Explicitly, Aa+Aa1+Aa2=r2π, and l1+l2+l3=2rπ, where r was the radius of the circle. If we subtracted the effect of surface tension from the pressure of air in the area of the bubble, we could get
![]()
![]()
![]() (8)
(8)
According to Eq.(7), on any section of the intact spherical bubble, the pressure of water was equal to the pressure of air minus the corresponding effect of surface tension. This gave
![]()
![]() (9)
(9)
Assuming l4≈l2 gave
![]() (10)
(10)
According to Laplace’s formula, there was
![]() (11)
(11)
The area of Aa1 plus the area of Aa2 would be smaller than the area of sector. Then, we could get
![]() (12)
(12)
where α was flare angle, as shown in Fig.4. If air bubble did not adhere on the soil grain, then α=0. η was a parameter representing the ratio of the area of the circle minus the area of the bubble to the area of the sector with flare angle α, maybe less than 1.
The force of surface tension along the circular arc in the soil grains could be expressed as
![]() (13)
(13)
Inserting Eqs.(9)-(13) into Eq.(8) yielded
![]() (14)
(14)
From Eq.(14), we can conclude that the bound bubbles are different from the suspending bubbles. Beside the pressure of water, there is the effect of surface tension.
Then, the total stress could be expressed as
![]() (15)
(15)
Equation (15) is the expression for effective stress for nearly saturated soils. If the effect of surface tension can be neglected, i.e., neglecting the last term in Eq.(15), the equation would be regressed to Eq.(4), that is, TERZAGHI’s formula of effective stress.
2.3 Effective stress in unsaturated soils with air bubbles in any shape
1) Deriving formula
If the degree of saturation became lower (air phase was still discontinuous while the water phase was continuous), air bubble embedded would not have a shape similar to sphere. The shape of air bubble might be the shape of soil pore. Picking a point in the soil and cutting by a plane, the pressure of pore water was constant to be uw, where the air phase was separated, ua,i was the pressure of one of air bubbles, and Aa,i was its area, as shown in Fig.5.
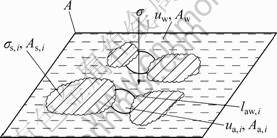
Fig.5 Each phase and its stress in section of point of soil when being surrounded by water
And then, the resultant force by the stress of each phase could be expressed as
![]() (16)
(16)
where law was the length of interface between air and water.
Because the interface between air and water would not be spherical face, according to Laplace’s formula, the relation between ua,i and uw could be expressed as
![]() (17)
(17)
where the last item was named as the additional pressure. ζ was a parameter. If the interface was spherical face, and R was the radius of sphere, then ζ=2; if the interface was cylinder, and R was the curvature radius of cylinder, then ζ=1; if the shape of interface was arbitrary, then ζ and R could be evaluated relevantly to make Eq.(17) come to existence (e.g.,![]() ,
, ![]() , where R1 and R2 were the curvature radii of two transversals in the arbitrary face which were perpendicular each other).
, where R1 and R2 were the curvature radii of two transversals in the arbitrary face which were perpendicular each other).
Inserting Eq.(17) into Eq.(16), the resultant force could be expressed as
![]()
![]() (18)
(18)
In order to simplify the above equation, according to Eq.(15), we could introduce a hypothesis: the force by additional pressure was equal to or more than the surface tension acting on the water/air interface, i.e.,
![]() (19)
(19)
Then, Aa could be divided into two parts: ![]() and
and ![]() It was appointed that
It was appointed that ![]() multiplied by the additional pressure was equal to surface tension. This gave
multiplied by the additional pressure was equal to surface tension. This gave
![]() (20)
(20)
And then
![]() (21)
(21)
Substituting the above equation into Eq.(18), and according to the above derivation, the formula of effective stress for unsaturated soils with air bubbles in any shape was given as
![]() (22)
(22)
where ![]() was named as “pore air elastic
was named as “pore air elastic
pressure”. It was part of the effect of the additional pressure (ua-uw). It had not direct relationship with degree of saturation. Considering simply, commonly with the decrease of the degree of saturation, pore air elastic pressure Ta increased.
2) Estimation of Ta
Transforming the expression of Ta gave
![]()
![]() (23)
(23)
where ua was the average pressure of air bubbles; a was parameter, and it could be expressed as
![]() (24)
(24)
When the pressures of every air bubbles were equal, a=1.
Comparing Eq.(21) with BISHOP’s formula, another expression of Ta could also be given as
![]() (25)
(25)
With the aid of Eq.(23), the parameter χ in BISHOP’s formula of effective stress could be expressed as
![]() (26)
(26)
where A was the whole area of section; ![]() was part of the area of pore air in the section. If the air bubble was suspended in the water, the value of
was part of the area of pore air in the section. If the air bubble was suspended in the water, the value of ![]() was equal to 0.
was equal to 0.
If air bubbles held the whole section of pore, then ![]() Noting that the average ratio of Aa/A on a set of parallel test planes passing through the sample equaled n(1-Sr), the minimum value of the parameter χ was given as
Noting that the average ratio of Aa/A on a set of parallel test planes passing through the sample equaled n(1-Sr), the minimum value of the parameter χ was given as
![]() (27)
(27)
where n was the porosity of soil, and Sr was the degree of saturation.
Substituting the above equation into Eq.(25) and considering Eq.(17), the maximum value of Ta was approximated to be
![]() (28)
(28)
where ![]() was the typical value of radius of curvature of the water/air interface Ri, and
was the typical value of radius of curvature of the water/air interface Ri, and ![]() was the typical value of parameters ζi.
was the typical value of parameters ζi.
Since parameters in Eq.(28) could not be directly measured or calculated, it was desirable to establish an approximation to these parameters based on some alternative average measures that were identifiable. For this purpose, supposing the diameter of pore, d, was in the same magnitude to ![]() Eq.(28) could be written to an approximation:
Eq.(28) could be written to an approximation:
![]() (29)
(29)
Assume some typical material parameters corresponding to clay, d=1 μm, n=0.5, Sr=90%, and T= 73×10-3 N/m, then Ta,max was estimated to be 3.65 kPa.
The value of Ta would not influence normal soils much but special soils such as sludge. Because of Ta, effective stress σ′ is less than (σ-uw). This must be the reason for a phenomenon observed by WICHMAN [19] when he researched the consolidation of gassy sludgy: the final degree of consolidation was less.
2.4 Effective stress in unsaturated soils with continuous air phase
If the degree of saturation became lower than the above phase, the air phase would be continuous while the water phase was discontinuous. The pressure of air was assumed to be ua. Because the water phase was separated, the pressure of one of water drops was assumed to be uw,i, and the area intercepted to be Aw,i, as shown in Fig.6.
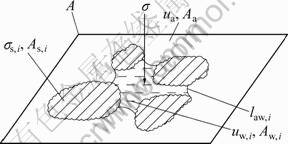
Fig.6 Each phase and its stress in section of point of soil when being surrounded by air
And then the resultant force by stress of each phase could be expressed as
![]() (30)
(30)
According to LAPLACE’s formula, the relation between uw,i and ua could be expressed as
![]() (31)
(31)
where the meanings of parameters were similar to Eq.(17).
Substituting the above equation into Eq.(30) resulted in
![]() (32)
(32)
where
![]() (33)
(33)
And then the formula of effective stress for air phase-continuous unsaturated soils containing free water was given as
![]() (34)
(34)
where
![]() (35)
(35)
If the pressure of pore air was equal to atmospheric pressure, then ua=0.
According to Eq.(33), Tw was constituted by two parts: one was caused by the additional pressure (ua-uw,i); the other was caused by the direct effect of surface tension. If we called Tw as suction, in the opinion of TANG et al [20], the first part of Tw was “matrix suction”, and the last one was “absorbed suction”. It was clear that the characteristics of these two parts were different. In addition, the value of Tw was subjected to content of pore water and the microstructure of soil, as we concluded from Eq.(33).
As was expressed in Eq.(34), Tw might also be regarded as a type of load to some extent.
If the soils contained no free water, or even no water, the applicability of surface tension should be limited.
3 Conclusions
1) Air bubble suspended in pore water does not influence TERZAGHI’s principle. But if bubbles are bounded to soil skeleton, bubbles do have their effect. However, the effect may be negligible. Therefore, TERZAGHI’s formula of effective stress need not be changed for nearly-saturated soils.
2) With the degree of saturation decreasing, air phase is still discontinuous, and the total stress can be constituted by effective stress, pore water pressure and pore air elastic pressure. These stresses all act on the whole section. The value of pore air elastic pressure is mainly relative to degree of saturation and diameter of pore.
3) When water phase is discontinuous, neutral stress is the air pressure. The concept of suction is proposed in the formula. But this suction refers to not only the matrix suction, but also the contract action by the “skin”. The value of suction is subjected to water content and microstructure of soil.
References
[1] KAYADELEN C. Estimation of effective stress parameter of unsaturated soils by using artificial neural networks [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(9): 1087-1106.
[2] JIE Yu-xin, WEN Qing-bo, LI Guang-xin, XU Yan-chun. Discussion on the principle of effective stress [J]. Journal of China Coal Society, 2005, 30(2): 202-205. (in Chinese)
[3] SHEN Zhu-jiang. No confusing fiction with reality-analysis of misunderstanding of some concepts in geotechnical engineering [J]. Chinese Journal of Geotechnical Engineering, 2003, 25(6): 767-768. (in Chinese)
[4] WEI Hai-yun, ZHAN Liang-tong, CHEN Yun-min. Compressibility and consolidation of unsaturated soils with high degree of saturation and its application [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(2): 264-269. (in Chinese)
[5] PIETRUSZCZAK S, PANDE G N. Constitutive relations for partially saturated soils containing gas inclusions [J]. Journal of Geotechnical Engineering, 1996, 122(1): 50-59.
[6] SILLS G C, WHEELER S J, THOMAS S D, GARDNER T N. Behavior of offshore soils containing gas-bubbles [J]. Geotechique, 1991, 41(2): 227-241.
[7] NUTH M, LALOUI L. Effective stress concept in unsaturated soils: Clarification and validation of a unified framework [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(7): 771-801.
[8] BISHOP A W. The principle of effective stress [J]. Tecknisk Ukeblad, 1959, 106(39): 859-863.
[9] KHALILI N, KHABBAZ M H. A unique relationship for chi for the determination of the shear strength of unsaturated soils [J]. Geotechique, 1998, 48(5): 681-687.
[10] BAO Cheng-gang, ZHAN Liang-tong. Relationship between unsaturated soil behavior and engineering problems [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(2): 129-136. (in Chinese)
[11] FREDLUND D G. Unsaturated soil mechanics in engineering practice [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(3): 286-321.
[12] SKEMPTON W W. Effective stress in soils, concrete and rocks [C]// Symposium on Pore Pressure and Suction in Soils. London: Butterworth, 1962: 4-16.
[13] CHEN Zheng-han, XIE Ding-yi, WANG Yong-sheng. Effective stress in unsaturated soil [J]. Chinese Journal of Geotechnical Engineering, 1994, 16(3): 62-69. (in Chinese)
[14] KHALILI N, KHABBAZ M H, VALLIAPPAN S. An effective stress based numerical model for hydro-mechanical analysis in unsaturated porous media [J]. Computational Mechanics, 2000, 26(2): 174-184.
[15] SHAHU J T. Effective stress behavior of quasi-saturated compacted cohesive soils [J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(4): 322-329.
[16] WHEELER S J. A conceptual model for soils containing large gas bubbles [J]. Geotechnique, 1988, 38(3): 389-397.
[17] LU N, GODT J W, WU D T. A closed-form equation for effective stress in unsaturated soil [J]. Water Resources Research, 2010, 46(5): W05515.
[18] BARDEN L. Consolidation of compacted and unsaturated clays [J]. Geotechnique, 1965, 15(3): 257-286.
[19] WICHMAN B G M. A finite strain theory for gassy sludge [J]. Geotechnique, 2000, 50(1): 35-41.
[20] TANG Lian-sheng, YAN Bo, ZHANG Peng-cheng, ZHAN Qing-hua. Definition and exploration for effective stress and related conception in unsaturated soil [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(2): 216-220. (in Chinese)
(Edited by YANG Bing)
Foundation item: Project(50878191) supported by the National Natural Science Foundation of China; Project(Y12E090030) supported by Zhejiang Provincial Natural Science Foundation, China
Received date: 2010-09-27; Accepted date: 2011-01-24
Corresponding author: XU Hao-feng, PhD Candidate; Tel: +86-574-88229512; E-mail: xuhaofeng@nit.zju.edu.cn
Abstract: BISHOP’s effective stress or two state stress variables are unsatisfactory for unsaturated soils where one of fluid phases is discontinuous, so new expressions of effective stress should be founded. The approach for derivation was according to the principle of equilibrium of forces (i.e., the stress-sharing principle), and it was firstly validated by demonstrating TERZAGHI’s principle of effective stress. And then, the derivations were subdivided into four parts according to different pore air states: 1) air bubbles were spherical and suspended in pore water; 2) air bubbles were bound on soil skeleton; 3) air bubbles held almost the single section of pore; 4) air phase was continuous. The different formulae of effective stress were presented. Conclusions are drawn as follows: 1) For nearly-saturated soils, the “real” effective stress would be a little smaller than TERZAGHI’s effective stress; 2) For soils in which air phase is discontinuous in the form of bubbles, a new concept of pore air elastic pressure is put forward, and the total stress can be constituted by effective stress, pore water pressure and pore air elastic pressure; 3) For soils in which air phase is continuous, effective stress is equal to the value of the total stress plus suction; 4) Suction can be divided into two parts: one is the effect caused by additional pressure, and the other is the contract action by the “skin”.
- Effective stress in soils under different saturation conditions


