
J. Cent. South Univ. (2021) 28: 556-571
DOI: https://doi.org/10.1007/s11771-021-4621-1

Micro-failure process and failure mechanism of brittle rock under uniaxial compression using continuous real-time wave velocity measurement
WU Zhi-jun(吴志军)1, WANG Zhi-yang(王智洋)1, FAN Li-feng(范立峰)2,WENG Lei(翁磊)1, LIU Quan-sheng(刘泉声)1
1. School of Civil Engineering, Wuhan University, Wuhan 430072, China;
2. College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract:
In this study, the micro-failure process and failure mechanism of a typical brittle rock under uniaxial compression are investigated via continuous real-time measurement of wave velocities. The experimental results indicate that the evolutions of wave velocities became progressively anisotropic under uniaxial loading due to the direction-dependent development of micro-damage. A wave velocity model considering the inner anisotropic crack evolution is proposed to accurately describe the variations of wave velocities during uniaxial compression testing. Based on which, the effective elastic parameters are inferred by a transverse isotropic constitutive model, and the evolutions of the crack density are inversed using a self-consistent damage model. It is found that the propagation of axial cracks dominates the failure process of brittle rock under uniaxial loading and oblique shear cracks develop with the appearance of macrocrack.
Key words:
Cite this article as:
WU Zhi-jun, WANG Zhi-yang, FAN Li-feng, WENG Lei, LIU Quan-sheng. Micro-failure process and failure mechanism of brittle rock under uniaxial compression using continuous real-time wave velocity measurement [J]. Journal of Central South University, 2021, 28(2): 556-571.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-021-4621-11 Introduction
Stress-induced failure is the main factor that induces instability problems in deep rock engineering [1-5]. Thus, the investigation of the micro-mechanism of rock failures during the loading process is of importance to practical applications. Typically, the failure process of brittle rocks under uniaxial compression can be described by a four-region model that is comprised of: 1) a region for closure of existing crack, 2) a stable crack growth region, 3) an accelerated crack growth region, and 4) a post-peak region [6, 7]. Accompanying the failure process, many physical properties such as the elastic modulus, permeability, electric resistance, elastic wave velocity and acoustic emission (AE) characteristics will also vary according to trends that depend on the failure stages [8-12]. Thereinto, the elastic wave velocity is more convenient to measure and highly sensitive to the nucleation and growth of cracks in the pore space of rocks [13, 14]. Due to the evolution of numerous cracks in brittle rocks during the damage development process, elastic wave velocity measurements have been used by many researchers to investigate the damage of brittle rock in deep rock engineering [15-19]. Therefore, the knowledge of the mechanism and the relationship between the wave velocity change and the internal damage evolution in brittle rocks is helpful to understand the failure behaviour in deep brittle rocks.
For this propose, laboratory experiments have been conducted to investigate the changes in elastic wave velocities in brittle rocks under various conditions. BONNER [20], LOCKNER et al [21], HADLEY [22], CHEN et al [23], PELLET et al [24] and ZUO et al [25] measured the variation of wave velocity of different type of brittle rocks under axial and triaxial compression test. These experiments have revealed that as a brittle rock is subjected to increasing differential stress, the wave velocity first increases due to the compaction of inner voids, and then decreases with damage development at higher differential stress that approaches rock failure. AYLING et al [26] and FORTIN et al [27, 28] studied the variation of wave velocity of brittle rocks under compression from the mesoscopic point of view. The results show that the increase of wave velocity is associated with the effect of pore collapse at a low stress level, and the wave velocity decreases when the mineral grains are crushed, which is very helpful for understanding the relationship between wave velocity variation and inner damage evolution. Schubnel et al [29], Fortin et al [30], Eslami et al [31], and Stanchits et al [32] studied the direction- dependent wave velocity variation in brittle rocks under compression, which is caused by the anisotropic damage evolution when a brittle rock is under compression. In addition, the influence of confining pressure was also studied by Stanchits et al [32], Birch [33, 34], and Christensen et al [35]. They found that the confining pressure can compact the rock specimen and prohibit the crack growth, which causes the initial wave velocities to exceed those under uniaxial loading conditions and causes the variations of the wave velocities to be gentler. These studies have made great contributions to identifying the mechanism of internal-damage- induced wave velocity variations under various loading conditions.
Based on the above researches, many models for describing the variation of the wave velocity with the damage evolution during the rock failure process have been proposed. By measuring wave velocities of granite specimens that were pre-damaged to various extents via cyclic loading, YAN et al [36] proposed a model for describing the relationship between the decrease of the wave velocity and the degradation of mechanical properties. By measuring the wave velocity and determining the microstructures of granite specimens that were damaged by various differential stress levels, ODA et al [37] and TAKEMURA et al [38] constructed a model that reflects the degradation of the wave velocity along with the increase of the crack density. Based on the observation of scanning electron microscopy (SEM) and wave-velocity measurements on thermal shocked granite specimens, ZHOU et al [39] proposed a model that states the relationship between wave velocity and the geometrical parameters of micro-fracture (length and quantity). However, in these studies, the wave velocities were measured under an unloaded stress state instead of during a real-time damage process; hence, the proposed models can hardly reflect the real failure process. Considering the close relationship between the permeability and the crack density, FORTIN et al [40] recorded the lateral wave velocities and permeability in sandstone samples under triaxial compression tests and proposed a quantitative model for describing the variation of the wave velocity with the crack density evolution. By simultaneously measuring the lateral wave velocities and volumetric strain in granite samples under triaxial compression tests, NICOLAS et al [41] constructed a model for quantitatively describing the relationship between the wave velocity degradation and the internal damage evolution. In these studies, the real-time measurement of the wave velocity improved the accuracy of the models. However, due to the absent consideration of the directional dependence of the wave velocity change and the damage evolution during uniaxial compression, these models cannot adequately reflect the failure process or reveal the failure mechanism of rock under uniaxial loading.
To evaluate the failure process and further reveal the failure mechanism of brittle rocks under uniaxial loading condition, continuous real-time measurements of elastic wave velocities are implemented on marble samples during uniaxial compression tests. A wave velocity model that considers the inner anisotropic crack evolution is proposed for describing the variations of wave velocities. Based on the wave velocity model, the variation of effective elastic parameters and crack densities in lateral and vertical directions are inferred, which provides more information of specimen failure process and is very helpful for revealing the failure mechanism of brittle rocks under the uniaxial loading. In addition, AE moment tensor inversion is performed to verify the effectiveness of this method.
2 Experimental
An intact marble block with a massive structure was collected from Hunan, China. The mineral types of the marble specimens include calcite (more than 95%), and other carbonate minerals including tremolite, plagioclase, quartz (less than 5%). The grain size of the marble ranges from 0.05 to 0.3 mm; hence, it is fine-grained. The apparent density was determined to be 2.82 g/cm3. Specimens of the marble were prepared in a cuboid shape of 80 mm 80 mm
80 mm 160 mm. The initial wave velocities of the specimens are measured prior to the formal test. A summary of the physical properties of the studied marble is presented in Table 1.
160 mm. The initial wave velocities of the specimens are measured prior to the formal test. A summary of the physical properties of the studied marble is presented in Table 1.
Table 1 Physical properties of specimens

Uniaxial compression tests were conducted on these specimens using a rock material test (RMT) system (Figure 1). During uniaxial compression, the axial piston was advanced at a constant displacement rate of 0.001 mm/s. The volumetric strain was estimated using three strain gauges that were glued directly onto the specimen surface in three orthogonal orientations, i.e., the x1, x2, x3 axis of the Cartesian coordinate system. Thus, the volumetric strain εv was calculated as: εv=ε1+ε2+ε3.
AE detection module PIC-2 of the DISP series, which was manufactured by Physical Acoustic Corporation, was used to record the AE behaviour.
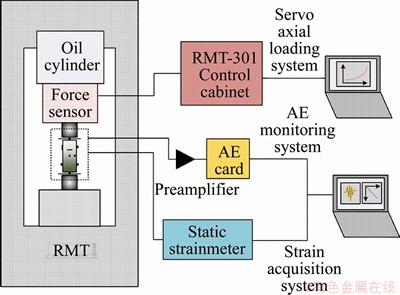
Figure 1 Experimental apparatus and measurement system
Eight AE piezoceramic transducers with a resonance frequency range of 100-400 kHz were directly mounted on the specimen surface. To reach a satisfactory acoustic coupling, a thin layer of vaseline was applied at the interface between the specimen and the AE transducer. The AE data acquisition parameters are summarized in Table 2.
Table 2 AE data acquisition parameters

These AE detection modules were also used to monitor the variations of the wave velocities during loading. The elastic wave velocities were measured using the pulse transmission method, which measures the travel time of a solitary elastic pulse through two piezoelectric detectors that are held in contact with a rock sample of known length. Via this approach, the P-wave velocities can be measured by the opposite transducers and the S-wave velocities can be measured by the coplanar transducers. In this experiment, four P-wave velocities and two S-wave velocities were measured by the eight AE transducers with a special distribution (Figure 2). The details of the AE transducer distribution and the transducer pairs for wave velocity measurements are presented in Tables 3 and 4, respectively. Elastic wave velocity measurements were executed during the loading process with an interval of 40 s. For periodic elastic wave velocity measurements, a group of high-frequency signals with 5 μs duration and 100 ms interval were pulsed on each transducer in sequence while the others were used as receivers. Considering that the AEs induced by rock failure may interfere with the pulse signal, it is necessary to suspend the mechanical loading during the wave velocity measurements. In order to measure the P-wave velocity in the x3 direction during axial compression testing, a pair of special cushion blocks were used in our experiments (Figure 2). The AE transducers were inlaid into the cushion blocks and directly mounted on the top and bottom surfaces of the specimen. As a consequence, the wave velocity can be measured during axial loading without damaging the transducers.
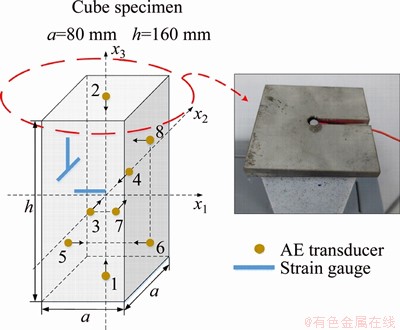
Figure 2 Locations of 8 transducers and 3 strain gauges on cuboid specimen surface
Table 3 Locations of sensors and transducer pairs for wave velocity measurements

Table 4 Transducer pairs for wave velocity measurements

3 Experimental results
The stress-strain relations of three tested specimens and the corresponding variations of the accumulated AE counts and the AE hit rate with the axial strain are presented in Figure 3. Because the results of the three specimens are very similar, only specimen 1 is chosen for detail analysis. It can be seen that there are two significant increments of the AE hit rate even in the logarithmic coordinates. The first increment is at the end of the compaction phase of the tested sample (about 0.2UCS). It represents that the sample has been compacted and microfracturing begins to stably develop. Hence, the stress level of this point is the crack initiation stress. The second increment is at the end of linear phase (about 0.75UCS), which means the accelerated and unstable crack growth. Thus, the stress level of that point is the crack damage stress [42-44]. Few AE hits are generated in the crack closure phase (Phase I) while the axial stiffness gradually increases with the closure of pre-existing cracks. In the crack initial phase (Phase II), AE hit rate rapidly increases and subsequently stabilizes at approximately 400 times per second, which indicates the stable crack initiation in the tested specimen. The axial stress increases almost linearly with the axial strain in this phase. In the crack damage phase (Phase III), the AE hit rate increases exponentially while the axial stiffness begins to decrease, which corresponds to the propagation and coalescence of cracks in the specimen. Finally, the specimen fails immediately when the axial stress reaches the maximum value and no significant post-peak region is observed. The results indicate that the ultimate failure of the specimen is caused by the rapid propagation and coalescence of unstable microcracks.

Figure 3 Evolution of axial stress, accumulated AE counts and AE hit rate with axial stress:
Figure 4 presents the evolution of the axial, lateral and volumetric strains during the uniaxial compression test. The characteristics exhibited by the recorded stress-strain curves depend on the loading phase. In the crack closure phase, comparing with the obvious increase of the axial strain, the decrease of the lateral strains is limited. As a result, the volumetric strain increases and reaches its maximum value near the crack initiation stress, which indicates that the per-existing cracks are compacted in this phase. In the crack initiation stress, the volumetric strain begins to decrease due to the accelerated decrease of the lateral strains, which indicates that axial cracks gradually initiate and open due to lateral tension. In the crack damage phase, as the axial stress further increases, the specimen rapidly dilates in the lateral direction, which corresponds to severe axial crack coalescence and axial splitting failure.

Figure 4 Evolution of axial, lateral and volumetric strains during uniaxial compression testing:
The variations of four P-wave velocities and two S-wave velocities are plotted in Figure 5. During uniaxial compression testing, wave velocities that differ in their directions of orientation exhibit distinct variation trends. In the crack closure phase, all wave velocities increase as the axial load increases. Among these P-wave velocities, the P33 velocity increases most, followed by Pθ and P11. For S-wave velocities, the S31 velocity increases more than the S12 velocity, indicating that the specimen is compacted with the preferential closure of lateral pre-existing cracks in this phase. In the crack initial phase, the P33 velocity and the S31 velocity maintain their increasing trends, which correspond to continuous compaction in the axial direction. Meanwhile, the P11 velocity and S12 velocity begin to decrease, which indicates the axial cracks gradually initiate and open due to lateral tension. In the crack damage phase, all the wave velocities decrease due to the internal damage evolution. Comparing with the slight decreases of the P33 and S31 velocities, the P11 and S12 velocities decrease more drastically, which indicates the severe crack evolution and coalescence in axial direction and the incidental development of oblique shear cracks during the crack damage phase.
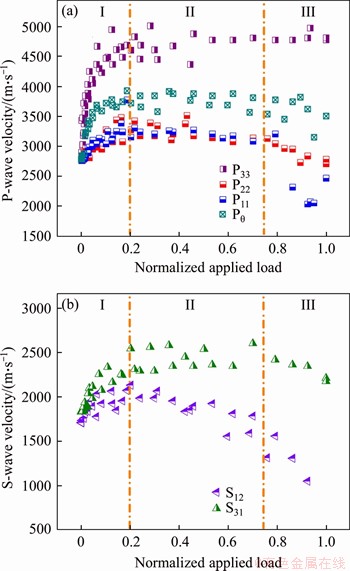
Figure 5 P-wave (a) and S-wave (b) velocities during uniaxial compression testing plotted as functions of axial stress
4 Discussion
4.1 Description of elastic wave velocities
Numerous experiments have indicated that the elastic wave velocities of rocks as a reaction to mechanical loading are mainly controlled in two ways: 1) the compaction of rock constituent, termed ‘intrinsic’ effects and 2) the variation of microcracks, termed ‘extrinsic’ effects [33]. The ‘intrinsic’ effects result in an approximately linear variation of elastic wave velocity with the stress state [45, 46] and the ‘extrinsic’ effects typically cause rapid nonlinear change of the wave velocity-pressure trend [33, 34]. Scholars have found that the ‘extrinsic’ effects of crack closure can be described by an exponential term [45, 47]. GREENFIELD et al [45] and FREUND [47] used a superposition of a linear term and an exponential term to describe the velocity-stress trend in rock material under hydraulic pressure, which corresponds to the effects of constituent compaction and crack closure respectively. The relation is expressed as follows:
V(σ)=a+bσ-cexp(-dσ) (1)
where the undetermined parameters, namely, a, b, c and d, are related to the physical state of the rock as follows: a is the crack-free velocity at zero pressure, b is the ‘intrinsic’ pressure derivate of crack-free specimen; c is the crack influence on the velocity; d is the crack closure parameter which represents the crack closure rate. Thus, the difference between a and c states is the zero pressure velocity.
In the case of uniaxial compression, in addition to the effects of rock compaction and crack closure, the wave velocity changes caused by crack initiation and propagation should also be considered. In this work, crack development is considered the reverse process of crack closure and described by an exponential term. Therefore, the elastic wave velocities that are measured in the uniaxial compression test can be described by a superposition of three terms: 1) a linear term for constitutive compaction, 2) an exponential term for crack closure and 3) another exponential term for crack development. Hereby, the elastic wave velocity can be expressed as a function of the axial stress as follows:
V(σ)=a+bσ-cexp(-dσ)-eexp(-f(UCS-σ)) (2)
where a is the crack-free wave velocity at zero pressure; b is associated with the ‘intrinsic’ effect on the wave velocity; c is the increased wave velocity that is caused by crack closure; d represents the crack closure rate; e is the decreased wave velocity that is caused by crack evolution; f represents the crack evolution rate.
Based on the above model, a crack closure parameter (λclo), which is expressed as the product of the wave velocity increment (parameter c) and its increase rate (parameter d), is introduced to reflect the level of crack closure. Analogously, the level of crack evolution is reflected by a crack evolution parameter (λevo) which is defined as the product of parameter e and parameter f. These parameters are expressed as follows:
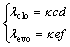 (3)
(3)
where κ is the correction factor, which is associated with the type of elastic wave. In this study, κ equals 1 for P-waves and 1.6 for S-waves.
The above wave velocity model is used to predict the variations of wave velocities with the axial stress during uniaxial compression. The simulated wave velocities, which are plotted in Figure 6, accord with the recorded wave velocities and the directionally dependent development of micro-damage can be clearly seen from the values of these associated parameters (which are listed in Table 5). Parameter b, which is positive in axially orientated waves (P33 and S31), decreases with the increase of inclination angle of the wave orientation and finally becomes negative in laterally orientated waves (P11 and S12). It is consistent with the axial compression and transverse tension of the specimen during uniaxial compression testing. For the crack closure parameter, the maximum value is attained in P33, followed by Pθ, S31, P11 and S12, which indicates that the level of crack closure also decreases with the increase of the inclination angle of the wave orientation. This result accords with the preferential closure of lateral pre-existing cracks in the crack closure phase. The variation trend of the crack evolution parameter is opposite that of the crack closure parameter. The minimum value is attained in P33 and the crack evolution parameter increases with the inclination angle of the wave orientation. The variation trend of the crack evolution parameter accords with the severe axial crack evolution during the crack damage phase. Based on the above analysis, not only the variations of the wave velocities during the uniaxial compression (rapid increase in the crack closure phase, and relative stability in the crack initiation phase, and decrease in crack damage phase) but also the direction- dependent micro-damage evolution is well described in this wave velocity model. Hence, the model can describe the elastic wave velocity versus uniaxial stress trends and well reflect the mechanism of wave velocity variation during uniaxial compression testing.
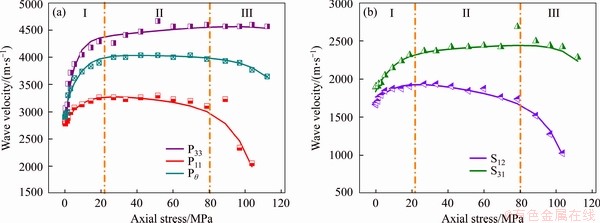
Figure 6 Description of varied P-wave (a) and S-wave (b) velocities according to proposed model
Table 5 Parameters for fitting to wave velocities in various directions according to Eq. (2)

According to Figure 6, the axial and lateral wave velocities differ substantially in terms of their variation trends during uniaxial compression testing. The observed anisotropy of the velocity field can be expressed by two parameters [48]:
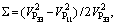
 (4)
(4)
Figure 7 shows the evolution of velocity anisotropy parameters as functions of the axial stress. The initial anisotropy of the rock is less than 2% for the P-wave velocity and less than 6% for the S-wave velocity. The anisotropy of the wave velocity continuously increases with the axial stress and finally approaches 50%. During the loading process, the anisotropy of the wave velocity increases rapidly in Phase I and Phase III. In Phase I, the rapid increase of the wave velocity anisotropy is mainly due to the difference in the crack closure degree between the axial and lateral directions. In Phase III, this behaviour is due to the large expansion of the axial cracks. According to evolutions of the anisotropy parameters during uniaxial compression, it can be concluded that the wave velocity anisotropy is mainly induced by the anisotropic damage development.

Figure 7 Evolution of velocity anisotropy parameters with axial stress
4.2 Evolution of effective elastic parameters
The elastic wave velocities and the mechanical properties are closely related in rock material. For brittle rock, the effects of viscosity and plasticity can be negligible. Thus, based on the theory of continuum mechanics, the transportation of elastic waves in a brittle rock can be described by the wave function of an elastic medium which is expressed as follows:
 (i, j, k, l=1, 2, 3) (5)
(i, j, k, l=1, 2, 3) (5)
where ρ is the rock density; Cijkl is the rock stiffness and u is the particle displacement vector. Considering an elastic wave that is travelling in one direction, the particle displacement vector ui can be expressed as follows:
 (i=1, 2, 3) (6)
(i=1, 2, 3) (6)
where ω is the circular frequency; V is the wave velocity; and (l1, l2, l3) is the direction vector of wave orientation. Substituting the above equation into the wave function (Eq. (5)) yields the relation between the wave velocity and the rock stiffness:
 (i, j, k, l=1, 2, 3) (7)
(i, j, k, l=1, 2, 3) (7)
We assume that prior to macro failure, the specimen can be approximated as a continuum. Then, the above theory can be used to obtain the effective elastic parameters of brittle rocks from the recorded wave velocities.
During uniaxial compression test, due to the special mechanical response (axial compression and lateral expansion), anisotropy develops in the specimen as the axial stress increases. The development of anisotropy in the x1-x3 plane was discussed in this section. As for x1-x2 plane, both the lateral strains and the lateral wave velocities in the x1 and x2 directions are similar. Hence, the elastic property in the lateral plane is approximately isotropic. Therefore, a transverse isotropic constitutive model is used to describe the elastic property of the specimen during uniaxial compression. The constitutive function is expressed as follows:
 (8)
(8)
where C11=C22, C44=C55 and C12=C11-C66. Only five independent elastic constants are sufficient for completely describing the transverse isotropic medium. Then, substituting the transverse isotropic stiffness into Eq. (7) yields the relationship between the wave velocity and the elastic constants. It is expressed in matrix form as follows:
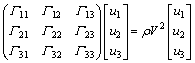 (9)
(9)
where Γij denotes the following determinants:
 (10)
(10)
Based on the above derivation, the effective stiffness tensor components can be calculated from the measured wave velocities. The five independent elastic constants are expressed as follows:

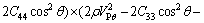
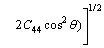 (11)
(11)
From the effective stiffness tensor, the effective elastic moduli, namely, E11 and E33, and the effective Poisson ratios, namely, υ12 and υ13, can be calculated as follows:

 (12)
(12)
where D is the following determinant:
 (13)
(13)
Figure 8 shows the evolutions of the effective elastic moduli E11 and E33, and the effective Poisson ratios υ12 and υ13 as functions of the axial stress. These effective elastic parameters exhibit different variation trends in the axial and lateral directions. The lateral effective elastic modulus E11 increases slightly in the crack closure phase and then begins to decrease when the axial stress exceeds the crack initial stress. Combined with the increase in the lateral effective Poisson ratio υ12, it is concluded that the specimen softens in the lateral direction during uniaxial compression testing. In the axial direction, except for the decrease prior to the final failure, effective elastic modulus E33 increases during the uniaxial compression test. Simultaneously, the axial effective Poisson ratio υ13 decreases during the loading process. Hence, the specimen hardens in the axial direction during uniaxial compression testing.

Figure 8 Evolution of effective elastic moduli (a) and Poisson ratios (b) with axial stress
The damage process of the compressed specimen can be inferred from the evolution of these effective elastic parameters. During uniaxial compression testing, the axial cracks gradually open and propagate due to the lateral expansion. As a consequence, in the lateral direction, the elastic modulus decreases and Poisson ratio increases with the increase of the axial stress. Although the crack initiation and propagation occur in the axial direction, they have little influence on the elastic modulus in the crack-parallel direction. At the same time, lateral cracks and constituents continue to be compacted by the increase of the uniaxial compression. Therefore, the axial elastic modulus gradually increases during uniaxial compression testing. The above inference accords with the conclusion from the variations of the wave velocities.
4.3 Inversion of crack density
We have discussed how the effective elastic modulus and the effective Poisson ratio change with the axial stress under uniaxial compression. In the following discussion, we invert the crack density using these effective elastic parameters.
Considering the strong anisotropy of the damage development in the failure process, it is necessary to invert the crack density separately for each direction. Based on the self-consistent approximation [49] and the penny-shaped crack damage model [50], the crack density evolution can be inverted through the variational effective elastic moduli and effective Poisson ratios. The crack densities in axial and lateral directions are expressed as follows:
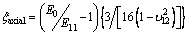 ,
,
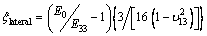 (14)
(14)
where ξ is the crack density; E is elastic modulus; υ is Poisson ratio; subscript 0 indicates the zero- pressure state. We used the initial effective elastic parameters prior to the deformation as reference values; therefore, the crack densities that are calculated here correspond to relative changes during deformation.
Figure 9 shows the changes in the relative crack densities in the axial and lateral directions during uniaxial compression testing. The variations of the crack density in the axial and lateral directions exhibit entirely different trends. In the crack closure phase, the axial crack density decreases because of the closure of oblique cracks induced by axial compression. Then, with the increase of the axial stress, axial cracks gradually open and stably initiate due to the lateral expansion. Therefore, the axial crack density begins to increase in the crack initial phase. With the severe axial crack coalescence in the crack damage phase, the axial crack density accelerates until the final failure. Simultaneously, due to the continuous axial compression, the lateral crack density continues to decrease during the crack closure phase and the crack initial phase. In the crack damage phase, oblique shear cracks develop with the coalescence of axial cracks. Thus, the lateral crack density increases slightly as the macro-crack prevails immediately prior to the final failure.
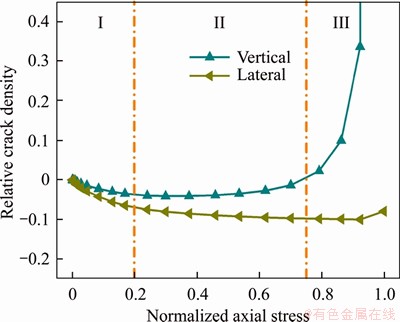
Figure 9 Inversion of crack density evolution during uniaxial compression testing
The failure process and failure mechanism can be identified from the evolutions of the axial and lateral crack densities. In summary, the failure process of brittle rock under uniaxial loading is mainly dominated by the closure of lateral cracks in the crack closure phase, the stable growth of axial cracks in the crack initial phase and the severe coalescence of axial cracks in the crack damage phase. Finally, the specimen is cleaved in the axial direction due to the accumulation and coalescence of axial cracks. In addition, the evolution of the crack density in the axial direction accurately reproduces the curves of the AE counts and the volumetric strain (Figure 3), and the above inversion is highly consistent with the observed failure pattern, which further proves that the failure process and failure mechanism can be successfully predicted via the proposed inversion method.
4.4 AE moment tensors inversion
AE technique has been used to study the failure mechanism of different rock types, and some significant results have been obtained [51-58]. In the following discussion, the failure mechanisms of marble under uniaxial compression is investigated from the AE point of view as a further verification the results of crack density inversion.
In order to determine the microcrack type, AE source location is first required. The original AE data are acquired by 8 sensors with uniform distribution (shown in Figure 10(a)), and the source location algorithm used here is Simplex algorithm, in which the optimization function between the observed onset time and the calculated onset time will be minimized.
 (15)
(15)
where Tobs and Tcal are the observed and calculated sensor onset time, respectively.
What calls for special attention is that the wave velocity is variable in both temporal and spatial domain. In temporal domain, the variation of wave velocity has been discussed in the former section. As for spatial domain, especially for transvers isotropic material, the wave velocity can be described as a function of Raypath angle [59].
 (16)
(16)
where V is modelled wave velocity as a function of Raypath angle, θ.
Based on the results of AE source location, the 3D-SIGMA [60] moment tensor inversion is executed in this discussion to solve the mode of AE events, the cracking motion vector (l) and the normal vector of the crack surface (n) (much detailed explanation can be found in Appendix).
The results of AE moment tensor inversion are shown in Figure 10(b). As can be seen, more AE events occur on the bottom half of specimen, which is consistent with the macroscopic damage in the failed specimen (shown in Figure 10(c)).
In order to further investigate the micro-failure process and failure mechanism, a statistical analysis is carried out onto these AE events. The temporal evolution of crack-type ratios is based on moving average of 100 events for better elucidating the changes along the testing time as shown in Figure 11(a). It can be seen that before 1003 s (about 0.9UCS) the damage pattern is of mainly tensile cracks. After that, the ration of shear crack obviously increases and becomes the main damage pattern. The directions of cracking motion vector (l) and the crack surface normal vector (n) of these events are also analyzed with a time threshold 1003 s. The vectors are categorized by the angle to the vertical direction, and the results are shown in Figures 11(b) and (c). Before 1003 s, the most frequent range of vector n is 70°-80°, which indicates that the damage at this time is dominated by vertical cracks. Besides, the direction distribution of vector l is quite similar as the distribution of vector n, which is the characteristics of tensile crack. After 1003 s, the most frequent range of vector n is 40°-50°. However, for vector l it is 60°-70°. It states that the oblique shear cracks develop with the coalescence of axial cracks when approaching the ultimate failure. The statistical analysis results agree well with the crack density inversion and the previous research [51].

Figure 10 (a) Distribution of AE transducers; (b) Overview of AE sources location; (c) Failed specimen

Figure 11 Temporal evolution of crack-type ratios (a), directional distribution of vector l and vector n before 1003 s (b), directional distribution of vector l and vector n after 1003 s (c)
5 Conclusions
To elucidate the micro-failure process and to reveal the failure mechanisms of a brittle rock, this study conducts uniaxial compression tests on marble specimens integrated with continuous real-time wave velocity measurements. Through the analysis of wave velocity data and the inversion of damage process, the following conclusion are drawn:
1) In the process of uniaxial compression, the evolutions of wave velocities become progressively anisotropic due to the direction-dependent development of micro-damage. A wave velocity model that considers the inner anisotropic crack evolution is proposed for describing the variations of wave velocities during uniaxial compression testing. In this model, both the variation of wave velocities and the direction-dependent micro- damage evolution process are well captured.
2) During uniaxial compression testing, as the axial load increases, the specimen softens (decreases in elastic modulus E11 and increases in Poisson ratio υ12) in the lateral direction and hardens (increases in elastic modulus E33 and decreases in Poisson ratio υ13) in the axial direction, which indicates that the crack closes in the lateral direction and propagates in axial direction with the increase of the axial load. This is consistent with the inference from the variations of the wave velocities.
3) During uniaxial compression testing, the axial crack density initially decreases in the crack closure phase, begins to increase in the crack initial phase, and finally drastically increases in the crack damage phase. Simultaneously, the lateral crack density continuous to decrease until the macro-crack prevails. The variations of the crack density in different directions demonstrate that the failure of the specimen under uniaxial compression is mainly induced by the accumulation and coalescence of axial cracks.
The experimental techniques and the associated results have shown promise in estimating the failure processes and the failure mechanisms of other brittle rocks. However, there are also some limitations in this study. Firstly, the influence of the confinements is neglected in this study, which always exists in natural condition and may lead to a different conclusion from the present study. Hence, biaxial/triaxial tests are needed in the further research. Then, some deep rocks may show viscosity and plasticity, and this method is unable to describe the failure processes of deep soft rocks that show obvious viscoplastic characteristics. Thus, an improved model with respect to the mechanical characteristics of soft rocks should be developed in the future. In addition, when using strain gauge measurements, only pre-peak stress-strain relations can be obtained, leading to a limited understanding on rock failure process related to wave velocity variations. The complete stress-strain relations with wave velocity measurements are needed to be conducted for further investigating micro-failure process and failure mechanism of brittle rocks.
Appendix
3D-SIGMA moment tensor inversion
The relationship between the observed AE amplitude and source moment is expressed as Eq. (A1)
 (A1)
(A1)
where A(x) is the observed amplitude; Cs is the magnitude of the sensor response; R is the distance from the source to sensor; rp and rq are the direction cosine; and Mpq is the moment tensor of source. Re(t,r) is the reflection coefficient which is expressed as:
 (A2)
(A2)
where t represents the orientation vector of sensor sensitivity which is assumed to be the normal vector of a sensor; k=Vp/Vs is the ratio of P-wave and S-wave velocity; and a is the scalar product of vectors r and t.
Once the moment tensor of an event is obtained, the eigenvalues and eigenvectors of the moment can be solved. The moment tensor decomposition procedure is accomplished by Eq. (A3).
 (A3)
(A3)
where e1, e2 and e3 are the maximum, intermediate, and minimum eigenvalues, respectively; X, Y and Z are the shear component, deviator component, and hydrostatic component of the source moment, respectively. The selected classification thresholds are, X/(X+Y+Z)>0.6 for the shear event, 0.4 Contributors The overarching research goals were developed by WU Zhi-jun, WANG Zhi-yang and FAN Li-feng. The laboratory tests were conducted by WANG Zhi-yang and WENG Lei. Theory and modelling part was finished by WANG Zhi-yang. The initial draft of the manuscript was written by WU Zhi-jun and WANG Zhi-yang. WU Zhi-jun, WENG Lei and WANG Zhi-yang replied to reviewers’ comments and revised the final version. The financial support is provided by foundation item of WU Zhi-jun and LIU Quan-sheng. Conflict of interest WU Zhi-jun, WANG Zhi-yang, FAN Li-feng, WENG Lei and LIU Quan-sheng declare that they have no conflict of interest. References [1] WENG Lei, HUANG Lin-qi, TAHERI A, LI Xi-bing. Rockburst characteristics and numerical simulation based on a strain energy density index: A case study of a roadway in Linglong gold mine, China [J]. Tunnelling and Underground Space Technology, 2017, 69: 223-232. DOI: 10.1016/ j.tust.2017.05.011. [2] ZHOU Xiao-ping, HUANG Xiao-cheng, LI Jin-xin. Reliability assessment of tunnel based on P-wave seismic velocity [J]. International Journal of Geomechanics, 2018, 18(11): 06018030. DOI: 10.1061/(ASCE)GM.1943-5622.00 01245. [3] LUO Yong, GONG Feng-qiang, LI Xi-bing, WANG Shan-yong. Experimental simulation investigation of influence of depth on spalling characteristics in circular hard rock tunnel [J]. Journal of Central South University, 2020, 27(3): 891-910. DOI: 10.1007/s11771-020-4339-5. [4] CHU Zhao-fei, WU Zhi-jun, LIU Quan-sheng, LIU Bao-guo. Analytical solutions for deep-buried lined tunnels considering longitudinal discontinuous excavation in rheological rock mass [J]. Journal of Engineering Mechanics, 2020, 146(6). DOI: 10.1061/(ASCE)EM.19437889.0001784. [5] WU Qiu-hong, LI Xi-bing, WENG Lei, LI Qing-feng, ZHU Yong-jian, LUO Rong. Experimental investigation of the dynamic response of prestressed rockbolt by using an SHPB-based rockbolt test system [J]. Tunnelling and Underground Space Technology, 2019, 93: 103088. DOI: 10.1016/j.tust.2019.103088. [6] BRACE W F, W PAULDING J B, SCHOLZ C H. Dilatancy in the fracture of crystalline rocks [J]. Journal of Geophysical Research, 1966, 71(16): 3939-3953. DOI: 10.1029/JZ071 i016p03939. [7] ZHAO X G, CAI M, WANG J, LI P F, MA L K. Objective determination of crack initiation stress of brittle rocks under compression using AE measurement [J]. Rock Mechanics and Rock Engineering, 2015. 48(6): 2473-2484. DOI: 10.1007/s00603-014-0703-9. [8] PATERSON M S, WONG Teng-fong. Experimental rock deformation-the brittle field [M]. Springer Science & Business Media, 2005. [9] HEAP M J, VINCIGUERRA S, MEREDITH P G. The evolution of elastic moduli with increasing crack damage during cyclic stressing of a basalt from Mt. Etna volcano [J]. Tectonophysics, 2009, 471(1, 2): 153-160. DOI: 10.1016/ j.tecto.2008.10.004. [10] YANG D S, QI X Y, CHEN W Z, WANG S G, YANG J P. Anisotropic permeability of coal subjected to cyclic loading and unloading [J]. International Journal of Geomechanics, 2018, 18(8): 04018093. DOI: 10.1061/(ASCE)GM.1943-562 2.0001229. [11] ZHANG Ying, LIU Yao-ru, TAO Zhuo-fu, ZHOU Hao-wen, YANG Qiang. Fractal characteristics and failure analysis of geomechanical model for arch dam based on acoustic emission technique [J]. International Journal of Geomechanics, 2019, 19(11): 04019119. DOI: 10.1061/ (ASCE)GM.1943-5622.0001502. [12] CHEN Geng-ye, LIN Yun-mei. Stress-strain-electrical resistance effects and associated state equations for uniaxial rock compression [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(2): 223-236. DOI: 10.1016/S1365-1609(03)00092-3. [13] SCHOLZ C H. Velocity anomalies in dilatant rock [J]. Science, 1978, 201(4354): 441-442. DOI: 10.1126/science. 201.4354.441. [14] WU Qiu-hong, WENG Lei, ZHAO Yan-lin, GUO Bao-hua, LUO Tao. On the tensile mechanical characteristics of fine-grained granite after heating/cooling treatments with different cooling rates [J]. Engineering Geology, 2019, 253: 94-110. DOI: 10.1016/j.enggeo.2019.03.014. [15] ZHOU Biao, XIE Xiong-yao, LI Yong-sheng. A structural health assessment method for shield tunnels based on torsional wave speed [J]. Science China: Technological Sciences, 2014, 57(6): 1109-1120. DOI: 10.1007/s11431- 014-5554-9. [16] KRAUB F, GIESE R, ALEXANDRAKIS C, BUSKE S. Seismic travel-time and attenuation tomography to characterize the excavation damaged zone and the surrounding rock mass of a newly excavated ramp and chamber [J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 70: 524-532. DOI: 10.1016/j.ijrmms. 2014.06.010. [17] XU Guang-li, LI Zhi-peng, SONG Sheng-wu, CHEN Wei-dong, ZHANG Shi-shu, DONG Jia-xing. Assessment methods and criterion of EDZ for underground caverns [J]. Journal of Central South University (Science and Techrology), 2017, 48(2): 418-425. DOI: 10.11817/j.issn. 1672-7207.2017.02.021. (in Chinese) [18] ONYEBUEKE E O, DURRHEIM R J, MANZI M S D, SEBOTHOMA S, ZHANG S E, STETTLER E. High-resolution integrated geophysical investigation at the Lancaster Gold Mine, Krugersdorp, South Africa [J]. Pure and Applied Geophysics, 2020, 177(10). DOI: 10.1007/s00024- 020-02529-6. [19] ZHOU Hui, QU Cheng-kun, HU Da-wei, ZHANG Chuan-qing, AZHAR M U, SHEN Zheng, CHEN Jun. In situ monitoring of tunnel deformation evolutions from auxiliary tunnel in deep mine [J]. Engineering Geology, 2017, 221: 10-15. DOI: 10.1016/j.enggeo.2017.02.011. [20] BONNER B P. Shear wave birefringence in dilating granite [J]. Geophysical Research Letters, 1974, 1(5): 217-220. DOI: 10.1029/GL001i005p00217. [21] LOCKNER D A, WALSH J B, BYERLEE J D. Changes in seismic velocity and attenuation during deformation of granite [J]. Journal of Geophysical Research, 1977, 80(33): 5374-5378. DOI: 10.1029/JB082i033p05374. [22] HADLEY KATE. VP/VS anomalies in dilatant rock samples [M]. Birkhauser, Basel, 1975. [23] CHEN Xiang, XU Zhao-yi. The ultrasonic P-wave velocity-stress relationship of rocks and its application [J]. Bulletin of Engineering Geology and the Environment, 2017, 76(2): 661-669. DOI: 10.1007/s10064-016-0866-6. [24] PELLET F L, FABRE G. Damage evaluation with P-wave velocity measurements during uniaxial compression tests on argillaceous rocks [J]. International Journal of Geomechanics, 2007, 7(6): 431-436. DOI: 10.1061/ASCE1532-3641(2007) 7:6(431). [25] ZUO Jian-ping, WEI Xu, SHI Yue, LIU Chang, LI Meng, WONG R H C. Experimental study of the ultrasonic and mechanical properties of a naturally fractured limestone [J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 125: 104162. DOI: 10.1016/j.ijrmms.2019. 104162. [26] AYLING M R, MEREDITH P G, MURRELL S A F. Microcracking during triaxial deformation of porous rocks monitored by changes in rock physical properties, I. Elastic-wave propagation measurements on dry rocks [J]. Tectonophysics, 1995, 245(3, 4): 205-221. DOI: 10.1016/ 0040-1951(94)00235-2. [27] FORTIN J, GU GUEN Y, SCHUBNEL A. Effects of pore collapse and grain crushing on ultrasonic velocities and Vp/Vs [J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B8). DOI: 10.1029/2005JB004005. [28] FORTIN J, STANCHITS S, DRESEN G, GU GUEN Y. Acoustic emission and velocities associated with the formation of compaction bands in sandstone [J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B10). DOI: 10.1029/2005JB003854. [29] SCHUBNEL A, NISHIZAWA O, MASUDA K, LEI X J, XUE Z, GUEGUEN Y. Velocity measurements and crack density determination during wet triaxial experiments on Oshima and Toki granites [M]. Springer, 2003: 869-887. [30] FORTIN J, STANCHITS S, VINCIGUERRA S, GU GUEN Y. Influence of thermal and mechanical cracks on permeability and elastic wave velocities in a basalt from Mt. Etna volcano subjected to elevated pressure [J]. Tectonophysics, 2011, 503(1, 2): 60-74. DOI: 10.1016/ j.tecto.2010.09.028. [31] ESLAMI J, GRGIC D, HOXHA D. Estimation of the damage of a porous limestone from continuous (P- and S-) wave velocity measurements under uniaxial loading and different hydrous conditions [J]. Geophysical Journal International, 2010, 183(3): 1362-1375. DOI: 10.1111/ j.1365-246X.2010.04801.x. [32] STANCHITS S, VINCIGUERRA S, DRESEN G. Ultrasonic velocities, acoustic emission characteristics and crack damage of basalt and granite [J]. Pure and Applied Geophysics, 2006, 163(5, 6): 975-994. DOI: 10.1007/ s00024-006-0059-5. [33] BIRCH F. The velocity of compressional waves in rocks to 10 kilobars: 1 [J]. Journal of Geophysical Research, 1960, 65(4): 1083-1102. DOI: 10.1029/JZ065i004p01083. [34] BIRCH F. The velocity of compressional waves in rocks to 10 kilobars: 2 [J]. Journal of Geophysical Research, 1961, 66(7): 2199-2224. DOI: 10.1029/JZ066i007p02199. [35] CHRISTENSEN N I, WANG H F. The influence of pore pressure and confining pressure on dynamic elastic properties of Berea sandstone [J]. Geophysics, 1985, 50(2): 207-213. DOI: 10.1190/1.1441910. [36] YAN Peng, ZHANG Chen, GAO Qi-dong, LU Wen-bo, CHEN Ming, ZHOU Chuang-bing. Acoustic wave test on mechanical properties variation of rocks under different damage degrees [J]. Rock and Soil Mechanics, 2015, 36(12): 3425-3432. DOI: 10.16285/j.rsm.2015.12.012. [37] ODA M, KATSUBE T, TAKEMURA T. Microcrack evolution and brittle failure of Inada granite in triaxial compression tests at 140 MPa [J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B10). DOI: 10.1029/ 2001JB000272. [38] TAKEMURA T, ODA M. Changes in crack density and wave velocity in association with crack growth in triaxial tests of Inada granite [J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B5). DOI: 10.1029/2004JB003395. [39] ZHOU Xue-fei, FAN Li-feng, WU Zhi-jun. Effects of microfracture on wave propagation through rock mass [J]. International Journal of Geomechanics, 2017, 17(9): 04017072. DOI: 10.1061/(ASCE)GM.1943-5622.0000947. [40] FORTIN J, SCHUBNEL A, GUEGUEN Y. Elastic wave velocities and permeability evolution during compaction of Bleurswiller sandstone [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(7, 8): 873-889. DOI: 10.1016/j.ijrmms.2005.05.002. [41] NICOLAS A, FORTIN J, REGNET J B, DIMANOV A, GUEGUEN Y. Brittle and semi-brittle behaviours of a carbonate rock: Influence of water and temperature [J]. Geophysical Journal International, 2016, 206(1): 438-456. DOI: 10.1093/gji/ggw154. [42] MARTIN C D, CHANDLER N A. The progressive fracture of Lac du Bonnet granite [C]// International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Elsevier. 1994. [43] BIENIAWSKI Z T. Mechanism of brittle fracture of rock: Part I—theory of the fracture process [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1967, 4(4). DOI: 10.1016/0148- 9062(67)90030-7. [44] MORADIAN Z, EINSTEIN H H, BALLIVY G. Detection of cracking levels in brittle rocks by parametric analysis of the acoustic emission signals [J]. Rock Mechanics and Rock Engineering, 2015, 49(3): 785-800. DOI: 10.1007/s00603- 015-0775-1. [45] GREENFIELD R J, GRAHAM E K. Application of a simple relation for describing wave velocity as a function of pressure in rocks containing microcracks [J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B3): 5643-5652. DOI: 10.1029/95jb03462. [46] ULLEMEYER K, NIKOLAYEV D I, CHRISTENSEN N I, BEHRMANN J H. Evaluation of intrinsic velocity-pressure trends from low-pressure P-wave velocity measurements in rocks containing microcracks [J]. Geophysical Journal International, 2011, 185(3): 1312-1320. DOI: 10.1111/ j.1365-246X.2011.05008.x. [47] FREUND D. Ultrasonic compressional and shear velocities in dry clastic rocks as a function of porosity, clay content, and confining pressure [J]. Geophysical Journal International, 1992, 108(1): 125-135. DOI: 10.1111/j.1365-246X.1992. tb00843.x. [48] THOMSEN L. Weak elastic anisotropy [J]. Geophysics, 1986, 51(10): 1954-1966. DOI: 10.1190/1.1442051. [49] BUDIANSKY B, O'CONNELL R J. Elastic moduli of a cracked solid [J]. International journal of Solids and structures, 1976, 12(2): 81-97. DOI: 10.1016/0020- 7683(76)90044-5. [50] KACHANOV M. Elastic solids with many cracks and related problems [J]. Advances in Applied Mechanics, 1993, 30: 259-445. DOI: 10.1016/s0065-2156(08)70176-5. [51] ZHOU Xiao-ping, ZHANG Jian-zhi. AE event rate characteristics of flawed granite: From damage stress to ultimate failure [J]. Geophysical Journal International, 2020, 222(2): 795-814. DOI: 10.1093/gji/ggaa207. [52] ZHOU Xiao-ping, ZHANG Jian-zhi, QIAN Qi-hu, NIU Yong. Experimental investigation of progressive cracking processes in granite under uniaxial loading using digital imaging and AE techniques [J]. Journal of Structural Geology, 2019, 126: 129-145. DOI: 10.1016/j.jsg.2019. 06.003. [53] ZHANG Jian-zhi, ZHOU Xiao-ping. Forecasting catastrophic rupture in brittle rocks using precursory AE time series [J]. Journal of Geophysical Research: Solid Earth, 2020, 125(8). DOI: 10.1029/2019jb019276. [54] ZHOU X P, LIAN Y J, WONG L N Y, BERTO F. Understanding the fracture behavior of brittle and ductile multi-flawed rocks by uniaxial loading by digital image correlation [J]. Engineering Fracture Mechanics, 2018, 199: 438-460. DOI: 10.1016/j.engfracmech.2018.06.007. [55] WU Chen, GONG Feng-qiang, LUO Yong. A new quantitative method to identify the crack damage stress of rock using AE detection parameters [J]. Bulletin of Engineering Geology and the Environment, 2020. DOI: 10.1007/s10064-020-01932-6. [56] RODRIGUEZ P, ARAB P B, CELESTINO T B. Characterization of rock cracking patterns in diametral compression tests by acoustic emission and petrographic analysis [J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 83: 73-85. DOI: 10.1016/j.ijrmms. 2015.12.017. [57] WENG Lei, WU Zhi-jun, LIU Quan-sheng. Influence of heating/cooling cycles on the micro/macrocracking characteristics of Rucheng granite under unconfined compression [J]. Bulletin of Engineering Geology and the Environment, 2019, 79(3): 1289-1309. DOI: 10.1007/ s10064-019-01638-4. [58] YANG Jing, MU Zong-long, YANG Sheng-qi. Experimental study of acoustic emission multi-parameter information characterizing rock crack development [J]. Engineering Fracture Mechanics, 2020, 232: 107045. DOI: 10.1016/j.engfracmech.2020.107045. [59] THOMPSON B D, YOUNG R P, LOCKNER D A. Fracture in westerly granite under ae feedback and constant strain rate loading: Nucleation, quasi-static propagation, and the transition to unstable fracture propagation [J]. Pure and Applied Geophysics, 2006, 163(5, 6): 995-1019. DOI: 10.1007/s00024-006-0054-x. [60] OHTSU M. Acoustic emission theory for moment tensor analysis [J]. Research in Nondestructive Evaluation, 1995, 6(3): 169-184. DOI: 10.1007/BF01606380. (Edited by YANG Hua) 中文导读 通过波速的连续实时监测研究单轴压缩时脆性岩石的细观损伤过程和损伤机制 摘要:本文通过对一种脆性岩石(大理石)单轴压缩过程中不同方向波速的实时连续测量研究其细观损伤发展过程和损伤机制。试验结果显示,在单轴压缩过程中,由于试件内部损伤发展在不同方向上的差异,使得其波速逐渐呈现各向异性。为了描述轴向加载过程中波速的变化,我们提出了一个与试件内部各向异性裂纹演化相关的波速模型。在此基础上,通过横贯各向同性的力学模型和自洽损伤模型可以得到该试件等效弹性参数和内部裂纹密度的变化。分析结果显示:在单轴压缩过程中,该脆性岩石的损伤破坏主要是由轴向裂纹的不断积累增多导致的;斜向剪切裂纹的快速增多伴随着宏观裂纹的出现。 关键词:弹性波波速;脆性破坏;单轴压缩;实时连续测量;各向异性损伤演化;理论与建模 Foundation item: Projects(41502283, 41772309) supported by the National Natural Science Foundation of China; Project(2017YFC1501302) supported by the National Key Research and Development Program of China; Project(2017ACA102) supported by the Major Program of Technological Innovation of Hubei Province, China Received date: 2020-07-26; Accepted date: 2020-10-21 Corresponding author: FAN Li-feng, PhD, Professor; Tel: +86-17801127161; E-mail: fanlifeng@bjut.edu.cn; ORCID: https://orcid.org/ 0000-0002-7744-692X  (A4)
(A4)
Abstract: In this study, the micro-failure process and failure mechanism of a typical brittle rock under uniaxial compression are investigated via continuous real-time measurement of wave velocities. The experimental results indicate that the evolutions of wave velocities became progressively anisotropic under uniaxial loading due to the direction-dependent development of micro-damage. A wave velocity model considering the inner anisotropic crack evolution is proposed to accurately describe the variations of wave velocities during uniaxial compression testing. Based on which, the effective elastic parameters are inferred by a transverse isotropic constitutive model, and the evolutions of the crack density are inversed using a self-consistent damage model. It is found that the propagation of axial cracks dominates the failure process of brittle rock under uniaxial loading and oblique shear cracks develop with the appearance of macrocrack.


