Influence of amorphous degree on crystallization kinetics of Zr60Al15Ni25 bulk metallic glass
MA Qiang, YAN Zhi-jie, HAO Wei-Xin, HU Yong
School of Materials Science and Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China
Received 28 June 2010; accepted 5 November 2010
Abstract:
The microstructure of as-cast Zr60Al15Ni25 bulk metallic glass was investigated by high-resolution transmission electron microscopy. It is found that there exist numerous short-range order regions (SRORs) in the metallic glass though it is identified to be amorphous by X-ray diffraction method. Furthermore, the amorphous degree shows a close correlation with the microstructure of corresponding mother ingot. The crystallization kinetics was investigated by differential scanning calorimetry under isochronal and isothermal conditions. The results show that the crystallization is triggered by the growth of the pre-existing SRORs and the growth is three-dimension diffusion-controlled. The amorphous degree of Zr60Al15Ni25 bulk metallic glass considerably influences its crystallization kinetics, namely, the more homogeneous distribution of atoms results in a more sluggish nucleation behavior.
Key words:
Zr60Al15Ni25 metallic glass; short-range order; crystallization kinetics;
1 Introduction
A metallic glass is metastable with respect to crystallization as it is heated beyond the glass transition temperature (Tg). Zr-based multicomponent bulk metallic glasses have high glass forming ability and exhibit a large supercooled liquid region (ΔTx, defined as the temperature region between Tg and the onset temperature of crystallization Tx)[1-4]. Their high thermal stability provides a large experimentally accessible time and temperature window to investigate the crystallization kinetics in the supercooled liquid. The influences of other elements on the crystallization of Zr-based amorphous alloys were widely investigated[5-6]. Through the isothermal investigation of the phase transformation within a time scale, a time— temperature—transformation (TTT) diagram for a metallic system can be obtained[7]. The knowledge of the progression of the crystallization with time can provide a deeper insight into the crystallization mechanism of a bulk metallic glass.
The atomic configuration of a metallic glass is the resultant of freezing liquid. It has been found that there exist short-range order regions (SRORs) in metallic glasses by high-resolution transmission electron microscopy (HRTEM) and molecular dynamics simulation[8-9]. Due to the structure heredity, the SRORs in a metallic glass inherit from the corresponding mother liquid alloy, and microstructure of a liquid alloy has heredity from the mother ingot. In this sense, the microstructure of the mother ingot will influence the amorphous degree of the corresponding metallic glass, and its crystallization kinetics. This will lighten the crystallization mechanism of amorphous alloys, which is not well explained within the frame of classical nucleation theory. However, few works have addressed on this aspect.
It has been reported that the Zr60Al15Ni25 metallic glass has a wide ΔTx as high as 77 K[1]. LI et al[10] investigated phase products during the crystallization by analytical transmission electron microscopy (ATEM) and X-ray diffraction (XRD). In the present work, the crystallization kinetics of Zr60Al15Ni25 bulk metallic glass is investigated by differential scanning calorimetry (DSC) under isochronal and isothermal conditions, and the influence of amorphous degree of the metallic glass on its crystallization kinetics is discussed.
2 Experimental
Ingots with nominal compositions of Zr60Al15Ni25 (mole fraction, %) were prepared by arc melting a mixture of metals Zr, Al and Ni (with purity of better than 99.9 % in mass fraction) in a water-cooled copper crucible under titanium-gettered argon atmosphere. To prevent composition segregation, the original ingots were remelted 4 times at 1 300 K, and were marked with A0. Then, two A0 ingots were repeatedly melted 6 and 12 times at 1 580 K, and the resultant ingots are marked A6 and A12, respectively. The time of each melting operation was 60 s. Under the same preparation conditions, plate specimens with a cross-section of 1 mm×10 mm and length about 50 mm were prepared by suction casting in a copper mold, and their amorphous nature was verified by X-ray diffraction (XRD) using Cu Kα radiation. For expression convenience, hereafter, the specimens cast from the ingots A0, A6 and A12 were marked with M0, M6 and M12, respectively. The microstructures of ingots were observed by optical microscopy. The amorphous microstructure was observed by HRTEM under an accelerating voltage of 200 kV (JEOL JEM-2100 F). The crystallization processes of metallic glasses were characterized under the conditions of isochronal and isothermal in a differential scanning calorimeter (NETZCH, DSC 404) under flowing high purity argon. In the case of isochronal tests, the DSC plots were recorded at the selected heating rates of 10-40 K/min. For the isothermal analysis, the samples were firstly heated at the rate of 50 K/min to the preset temperature, and then held for a certain period until the completion of crystallization. The Al2O3 and Al pans were utilized for the isochronal and isothermal tests, respectively.
3 Results
The results of chemical analyses indicate that the compositions of ingots do not change after the repeated melting, which excludes the influence of the changes of compositions, especially the content of oxygen, on the crystallization kinetics. Fig.1 shows the microstructures of the ingots A0, A6 and A12. It is clear that the ingot microstructure becomes finer and finer with increasing repeated melting times. Fig.2 shows the XRD patterns of the as-cast specimens M0, M6 and M12, indicating their amorphous nature. The HRTEM images of glasses M0 and M12 are shown in Fig.3, indicating existence of SRORs in the metallic glasses. Based on the statistical mechanism, the calculated Gibbs energy of liquid Zr-Al-Ni system shows that Zr2Ni clusters prefer to exist[11]. Therefore, it is reasonably assumed that these
Fig.1 Microstructures of ingots A0 (a), A6 (b) and A12 (c)
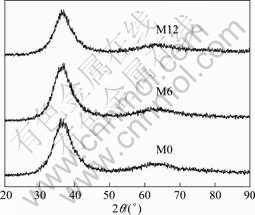
Fig.2 XRD patterns of as-cast specimens M0, M6 and M12
SRORs are Zr2Ni-like clusters. The average size of SRORs in M12 (about 3 nm) is much smaller than that in M0 (about 7 nm), suggesting that the distribution of atoms in M12 is more homogeneous than that in M0. Within the frame of classical homogeneous nucleation theory, the critical radius of a nucleus during crystallization of a metallic glass was estimated to be about 1 nm[12]. Then, it is reasonable to consider that the size of SRORs in the Zr60Al15Ni25 bulk metallic glass is overcritical.
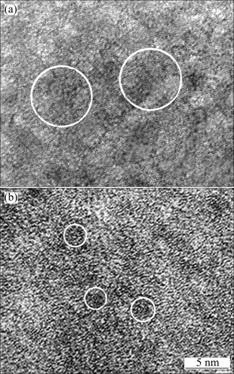
Fig.3 HRTEM images of glasses M0 (a) and M12 (b), showing existence of numerous of short-range order regions
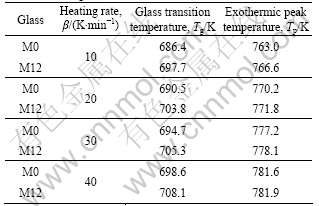
The isochronal DSC plots at the heating rates of 10, 20, 30 and 40 K/min are shown in Fig.4. All the DSC traces show an endothermic event, which is the characteristic of glass transition, followed by a single exothermic event corresponding to the crystallization process. The detailed DSC results of the glasses M0 and M12 are shown in Table 1.
From Table 1, it can be seen that the peak temperature of crystallization (Tp) increases with increasing heating rate. The effective activation energy for the crystallization (Ec) can be evaluated by Kissinger equation [13]:
(1)
where β is the heating rate; R is the gas constant; c is the constant. The Kissinger plots 
vs. 1/Tp (Fig.5) are approximately straight lines. Based on the slope of these Kissinger plots, the effective activation energies for crystallization (Ec) of glasses M0 and M12 are evaluated to be 345 kJ/mol and 431 kJ/mol, respectively. The
Fig.4 Isochronal DSC plots of glasses M0 (a) and M12 (b) at different heating rates
Table 1 Isochronal DSC data of glasses M0 and M12 at different heating rates
results indicate that the thermal stability of Zr60Al15Ni25 bulk metallic glass substantially improves due to the repeated melting.
The isothermal DSC traces exhibit a single exothermic peak after a certain incubation period (as exemplified by M0 in Fig.6). The detailed isothermal DSC results of M0 and M12 are shown in Table 2. It can be seen that the incubation time τ (defined as the time scale between the time t0 and t1%, t0 is the time to reach
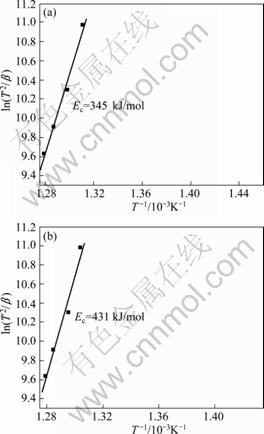
Fig.5 Kissinger plots of glasses M0 (a) and M12 (b)
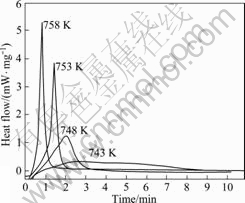
Fig.6 Isothermal DSC plots of glass M0 at different annealing temperatures
the annealing temperature, and t1% is the time to reach 1 % crystallized volume fraction) is considerably short at different annealing temperatures, which is attributed to the relatively high annealing temperatures. The value of τ increases when the annealing temperature decreases. Meanwhile, the exothermic peak width (referred to the time between 1 % and 95 % of transformation into the crystalline state) increases substantially, indicating a more sluggish crystallization process.
It is assumed that the crystallized volume fraction x, up to any time t, is proportional to the partial area of the exothermic peak. Thus the crystallized volume fraction corresponding to a given time during crystallization can be determined by measuring the partial area of the exothermic peak. The plots of the measured results at different temperatures are shown in Fig.7 (M0 and M12). The curves are typical sigmoid type. The time evolution of the crystallized volume fraction can be modeled by the Johnson-Mehl-Avrami (JMA) equation as follows[14-15]:
(2)
where x(t) is crystallized volume fraction; t is the annealing time; n (called as Avrami exponent) is a constant related to the behavior of nucleation and growth, and k is a reaction rate constant which depends on temperature T and effective activation energy Ec:
(3)
where k0 is a constant, and R is the gas constant.
Based on Eq.(2), an equation can be deduced as
(4)
By plotting 
vs.
at different annealing temperatures using the data x = 15%-85%, the JMA plots can be obtained and shown in Fig.8 (M0 and M12). The plots are nearly straight lines. The Avrami exponent n and the reaction rate constant k can be calculated from the slope and intercept of the lines and the detailed results are shown in Table 2.
Table 2 Isothermal kinetic parameters of glasses M0 and M12 at different annealing temperatures
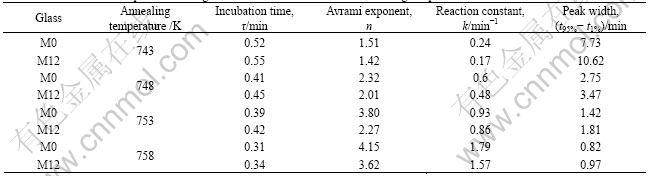
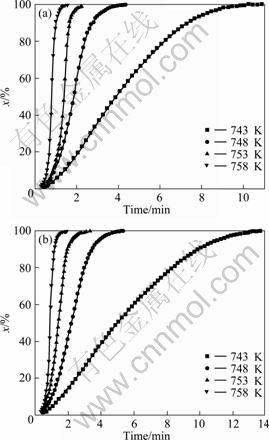
Fig.7 Crystallized volume fraction as function of annealing time for glasses M0 (a) and M12 (b) at different temperatures
For a glass, the obvious variation of Avrami exponent (Fig.8) indicates a change of mechanism of crystallization at different annealing temperatures. At the same annealing temperature, the Avrami exponent of glass M0 is larger than that of M12, implying a change of the crystallization mechanism.
4 Discussion
4.1 Short-range order regions in as-cast metallic glasses
The atomic configuration of an amorphous phase is similar to that of the liquid from which it is frozen. Thus the liquid structure influences the amorphous degree. The microstructure of mother ingot obviously becomes much finer after the repeated melting treatment (Fig.1). Due to the structure heredity, it is assumed that the atomic distribution is more homogeneous in the liquid, from which the amorphous specimens are produced when the ingot with finer microstructure is remelted to the same casting temperature. After the subsequent casting, the average size of the SRORs frozen in the corresponding amorphous phase becomes smaller, which is shown in HRTEM images (Fig.3). These SRORs, so-called
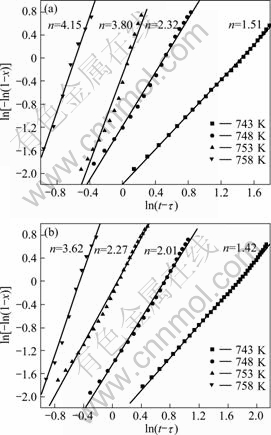
Fig.8 JMA plots for glasses M0 (a) and M12 (b) at different annealing temperatures
quenched-in nuclei, greatly influence the crystallization kinetics.
4.2 Crystallization kinetics under isochronal condition
As we know that, after the repeated melting of the mother ingot at 1 580 K, the effective activation energy for crystallization of the corresponding metallic glass obviously increases (Fig.5), which is attributed to the more homogeneous distribution of the atoms in the metallic glass. The results are consistent with our previous work[16]. The crystallization needs redistribution of atoms. The more homogeneous distribution of atoms results in more difficult redistribution of atoms, and therefore, larger effective activation energy (Fig.5).
4.3 Crystallization kinetics under isothermal condition
The isothermal crystallization kinetics was investigated at supercooled liquid state (between 743 K and 758 K). The Avrami exponent n provides the characteristics of nucleation and growth during the crystallization. The JMA parameters can be expressed in terms of the nucleation and growth parameters [17]. The Avrami exponent, n, can be expressed as
(5)
where a is the nucleation index (a = 0 for the nucleation rate of zero; 0 < a < 1 for a decreasing nucleation rate with time; a = 1 for a constant nucleation rate; and a > 1 for an increasing nucleation rate), b is the dimensionality of the growth (whose value can be 1, 2 or 3) and c is the growth index (c = 1 for interface-controlled growth and c = 0.5 for diffusion-controlled). The smallest value of n is about 1.5 (Table 2). Based on the discussion above, it can be known that the growth is diffusion-controlled during the crystallization, indicating c = 0.5. From Eq.(5), it can be known that the values of b for the glasses M0 and M12 at different temperatures can be modeled by 3. Therefore, the growth is three-dimension diffusion- controlled.
In a multicomponent system, each of the elements has its own diffusion coefficient, and consequently, different elements will generate different concentration gradients. As one of the elements diffuses much more slowly than the rest, its diffusion controls the actual growth rate. When the atom fluxes through the interface are driven by the steady state diffusion, the so-called diffusion-controlled growth is obtained. For the diffusion-controlled growth, 1
5 Conclusions
1) The repeated melting treatment results in an ingot with finer microstructure, and the atomic distribution in the corresponding Zr60Al15Ni25 metallic glass is more homogeneous.
2) The Avrami exponents indicate that the crystallization of Zr60Al15Ni25 bulk metallic glass starts from the growth of pre-existing overcritical short-range order regions (nuclei), and the growth is three-dimension diffusion-controlled.
3) The amorphous degree greatly influences its crystallization kinetics, namely, the more homogeneous distribution of atoms results in larger effective activation energy for crystallization in the glass M12, and therefore, a more sluggish crystallization behavior.
References
[1] INOUE A, ZHANG T, MASUMOTO T. Zr-Al-Ni amorphous alloys with high glass transition temperature and significant supercooled liquid region [J]. Mater Trans, JIM, 1990, 31: 177-183.
[2] INOUE A, ZHANG T, NISHIYAMA N, OHBA K, MASUMOTO T. Preparation of 16 mm diameter rod of amorphous Zr55Al7.5Ni10Cu17.5 alloy [J]. Mater Trans, JIM, 1993, 34: 1234-1237.
[3] PEKER A, JOHNSON W L. A highly processable metallic glass: Zr41.2Ti13.8Cu12.5Ni10.0Be22.5 [J]. Appl Phys Lett, 1993, 63: 2342-2344.
[4] INOUE A, ZHANG Q S, ZHANG W, YUBUTA K, SON K S, WANG X M. Formation, thermal stability and mechanical properties of bulk glassy alloys with a diameter of 20 mm in Zr-(Ti,Nb)-Al-Ni-Cu system [J]. Mater Trans, 2009, 50: 388-394.
[5] SAIDA J, SETYAWAN A D, MATSUSHITA M, INOUE A. Effect of Nb on transformation kinetics and mechanical properties in Zr-Al-Ni-Cu metallic glasses [J]. Mater Trans, 2010, 51: 1188-1193.
[6] YU ZH, DING D, LU T, XIA L, DONG Y D. Effect of minor Al addition on glass-forming ability and thermal stability of Zr-Cu binary alloy [J]. Mod Phys Lett B, 2010, 24: 2143-2150.
[7] KIM Y J, BUSH R, JOHNSON W L, RULISON A J, RHIM W K. Experimental determination of a time-temperature-transformation diagram of the undercooled Zr41.2Ti13.8Cu12.5Ni10.0Be22.5 alloy using the containerless electrostatic processing technique [J]. Appl Phys Lett, 1996, 68: 1057-1059.
[8] WANG S Y, WANG C Z, LI M Z, HUANG L, OTT R T, KRAMER M J, SORDELET D J, HO K M. Short- and medium-range order in a Zr73Pt27 glass: Experimental and simulation studies [J]. Phys Rev B, 2008, 78: 184204.
[9] HUI X D, LIU X J, GAO R, HOU H Y, FANG H Z, LIU Z K, CHEN G L. Atomic structures of Zr-based metallic glasses [J]. Sci China Ser G, 2008, 51: 400-413.
[10] LI C F, SAIDA J, MATSUSHIDA M, INOUE A. Crystallization process of Zr60Al15Ni25 amorphous alloy [J]. Mater Lett, 2000, 44: 80-86.
[11] LI H Q, YANG Y S, TONG W H, WANG Z Y. Gibbs energy calculation of liquid Zr-Al-Ni and Zr-Al-Cu-Ni alloys with clusters [J]. J Mater Sci, 2007, 42: 4060-4065.
[12] CLAVAGUERA-MORA M T, CLAVAGUERA N, CRESPO D, PRADELL T. Crystallization kinetics and microstructure development in metallic systems [J]. Prog Mater Sci, 2002, 47: 559-619.
[13] KISSINGER H E. Reaction kinetics in differential thermal analysis [J]. Anal Chem, 1957, 29: 1702-1706.
[14] JOHNSON M A, MEHL R F. Reaction kinetics in processes of nucleation and growth [J]. Trans Am Inst Min, Metall Pet Eng, 1939, 135: 416-458.
[15] AVRAMI M. Granulation, phase change and microstructure: Kinetics of phase change III [J]. J Chem Phys, 1941, 9: 177-184.
[16] YAN Z J, LI J F, HE S R, WANG H H, ZHOU Y H. Effect of repeated melting of the ingots on the glass forming ability of Zr-based alloys [J]. Mater Lett, 2003, 57: 2829-2833.
[17] RANGANATHAN S. The three activation energies with isothermal transformations: applications to metallic glasses [J]. J Mater Sci, 1981, 16: 2401-2404.
[18] CHRISTIAN J W. The theory of transformations in metals and alloys: Part I [M]. Oxford: Pergamon Press, 1975.
Zr60Al15Ni25大块非晶合金的无序程度对晶化动力学的影响
马 强, 闫志杰, 郝维新, 胡 勇
太原科技大学 材料科学与工程学院，太原 030024
摘 要：采用高分辨率电镀观测铸态Zr60Al15Ni25的微观结构。X-射线分析表明，铸态Zr60Al15Ni25合金为非晶态，而通过高分辨电镜发现非晶合金中存在大量的短程有序区。实验发现，非晶合金的无序程度与相对应的母合金铸锭的凝固组织密切相关。通过差示扫描量热法研究非晶合金在线性加热和等温条件下的晶化动力学。结果表明：非晶合金的晶化是预先存在的短程有序区作为晶核长大开始的三维扩散控制的过程。Zr60Al15Ni25块体非晶合金的无序程度对其晶化动力学具有明显的影响，即无序程度越大，非晶合金的晶化越迟缓。
关键词： Zr60Al15Ni25金属玻璃；短程有序；晶化动力学
(Edited by LI Xiang-qun)
Foundation item: Project (50804032) supported by the National Natural Science Foundation of China; Project (2008011046) supported by the Natural Science Foundation of Shanxi Province, China; Project (20080321036) supported by the Key Technologies R & D Program of Shanxi Province, China
Corresponding author: YAN Zhi-jie; Tel: +86-351-6998062; Fax: +86-351-6998256; E-mail: yanzhijie74@sohu.com
DOI: 10.1016/S1003-6326(11)60713-9
