J. Cent. South Univ. Technol. (2008) 15(s1): 582-588

DOI: 10.1007/s11771-008-426-8

Effects of stress and physical ageing on nonlinear creep behavior of poly(methyl methacrylate)

ZHAO Rong-guo(赵荣国)^{1, 2}, CHEN Chao-zhong(陈朝中)¹, LI Qi-fu(李其抚)¹, LUO Wen-bo(罗文波)^{1, 2}

(1. Institute of Rheological Mechanics, Xiangtan University, Xiangtan 411105, China;

2. Key Laboratory of Low Dimensional Materials and Application Technology of Ministry of Education,

Xiangtan University, Xiangtan 411105, China)

Key words:

creep; time-stress equivalence; time-ageing time equivalence; physical ageing; polymer；

1 Introduction

Poly(methyl methacrylate), as a thermoplastic poly- mer, has many excellent properties, such as excellent clarity and ultraviolet resistance, good abrasion resis- tance, hardness and stiffness, low water absorption, low smoke emission, good track and arc resistance, and is widely used in many kinds of structures, such as lenses, light covers, glazing (particularly in aircraft), light pipes, meter covers, bathroom fittings, outdoor signs, skylights, baths, toys.

When a polymeric material is annealed at above its glass transition temperature, T_g, for a period of time, and then quenched down to a temperature below its T_g and above its first secondary transition temperature T_β, the material is in a thermodynamic non-equilibrium state, its structure will evolve toward equilibrium state even under isothermal conditions, accompanying the change in thermal and mechanical properties with ageing time, t_e. The effects observed are called “physical ageing”^[1]. Physical ageing is a universal phenomenon which can affect the rheological behavior of most polymers. The physical ageing of polymeric material is often described using the enthalpy and volume change^[2-3] in a specimen treated by isothermal annealing and quenching, or tested by measuring creep compliance^[4-5]. Besides temperature, moisture, and pressure, physical ageing also dramatically changes the polymer’s intrinsic time, so the long-term creep compliances at various ageing times can be constructed by horizontal shift on the logarithmic timescale using the time-ageing time equivalence^[6]. To short-term creep tests, the effect of structural relaxation is inapparent, and the physical ageing can usually be ignored, but, for long duration tests or under service condition, the additional effect due to physical ageing incurred during the testing or service period must be taken into consideration^[7]. In recent years, the physical ageing mechanism and the effect of physical ageing on the properties of polymers have received more and more research attention, and many significant results have been gained^[8-10].

Considering the effect of temperature on intrinsic time of viscoelastic material, the time-temperature super- position principle^[11] was presented, and generalized as the time-stress superposition principle^[12], the time- moisture superposition principle^[13]. These principles suggest that the mechanical behavior of viscoelastic materials at different timescales can be made equivalent by changing their load level or service environment, and have been using to estimate the long-term mechanical behavior of polymers at room temperature or of metals at elevated temperatures^[14-17]. To construct a smooth master curve, sometimes it is necessary to take the effect of stress-induced damage on the long-term creep behavior of polymers into account^[18].

In this work, the effects of stress, ageing time and ageing temperature on creep behavior of poly(methyl methacrylate) were investigated, and the time-ageing time equivalence and the time-stress equivalence were applied to construct the master creep compliance curves.

2 Experimental

2.1 Specimen preparation

Commercial poly(methyl methacrylate) (PMMA), whose glass transition temperature is about 105 ℃, were used in this work. The specimens were machined from a PMMA sheet and made into the shape of dumbbell with dimensions of 10 mm×2 mm×60 mm in the gauge zone, annealed at 115 ℃ for 30 min, quenched and aged at different ageing temperatures for different ageing times varying from 2 to 120 h. The ageing temperature varied from 40 ℃ to 60 ℃. The annealing procedure with respect to subsequent thermal treatments is shown in Fig.1. At the end of each ageing process, short-term creep tests with 2 h duration at various stress levels ranging from 14 to 30 MPa were carried out on a CSS-44020 Universal Electronic Test Machine at room temperature.

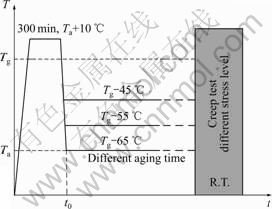
Fig.1 Schematic of thermal treatments and creep tests

2.2 Creep strain measurement

During the creep tests, the bottom base of the test machine maintained zero displacement, and the upper chuck moved along the axial direction upwards. The uniaxial tensile load imposed on the specimen was up to a constant rapidly and then sustained this load level, thus the creep strain occurred following the instantaneous strain. The constant stress was calculated as the ratio of constant load to initial area, the corresponding strain is determined as the ratio of the relative displacement between the two ends of the gauge length to the initial gauge length, and the creep compliance was defined as the ratio of time dependent strain to the imposed constant stress.

3 Construction of master curve

3.1 Time-ageing time equivalence

In the case of ageing temperature 40 ℃, the cruves of PMMA specimens’ creep compliance vs time at different ageing times ranging from 2 to 120 h under 14, 18, 22, 26 and 30 MPa are individually shown in Fig.2(a) to Fig.6(a), the curves at various ageing times and stress levels for the case of ageing temperature 50 ℃ are given in Fig.7(a) to Fig.11(a), and the creep curves for PMMA specimens at ageing temperature 60 ℃ are plotted in Fig.12(a) to Fig.16(a), respectively. It can be found from those figures that the compliance curves are dependent on ageing time, resulting in different compliances at different ageing time.

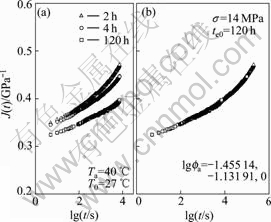
Fig.2 Creep compliance vs time at T_a=40 ℃, σ=14 MPa

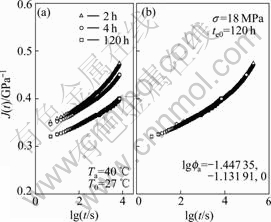
Fig.3 Creep compliance vs time at T_a=40 ℃, σ=18 MPa

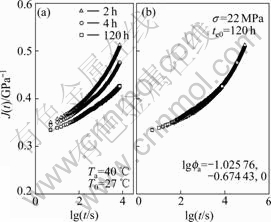
Fig.4 Creep compliance vs time at T_a=40 ℃, σ=22 MPa

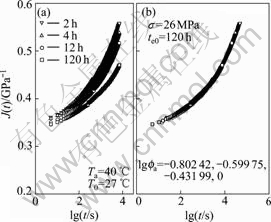
Fig.5 Creep compliance vs time at T_a=40 ℃, σ=26 MPa

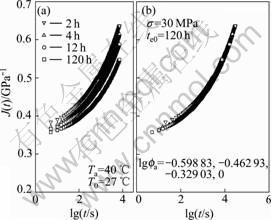
Fig.6 Creep compliance vs time at T_a=40 ℃, σ=30 MPa

The master creep compliance curves are superposed by horizontal shifts along logarithmic timescale via time-ageing time equivalence. To obtain the master curves, the reference ageing time chosen for this work is 120 h, and the ageing time shift factors,  are calculated by the least deviation between the reference creep curve and the shifted one. In the case of ageing temperature 40 ℃, the constructed master creep curves at reference ageing time 120 h for 14, 18, 22, 26 and 30 MPa are shown in Fig.2(b) to Fig.6(b).

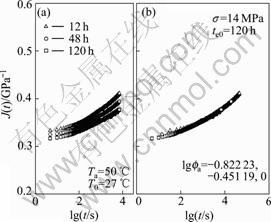
Fig.7 Creep compliance vs time at T_a=50 ℃, σ=14 MPa

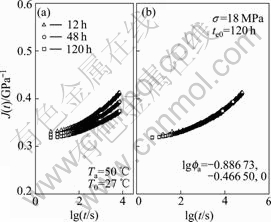
Fig.8 Creep compliance vs time at T_a=50 ℃, σ=18 MPa

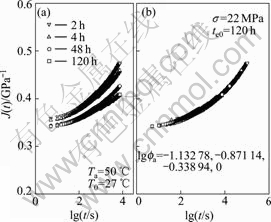
Fig.9 Creep compliance vs time at T_a=50 ℃, σ=22 MPa

In terms of time-ageing time equivalence, the creep compliance at the loading time t with an ageing time t_e will be equivalent to the creep compliance at time ξ with reference ageing time t_e^ref by setting  In the case of ageing temperature 50 ℃, the overlapped master creep compliance curves at reference ageing time 120 h for 14, 18, 22, 26, and 30 MPa are shown in Fig.7(b) to Fig.11(b), respectively, and the ageing time shift factors are calculated and shown in the figures.

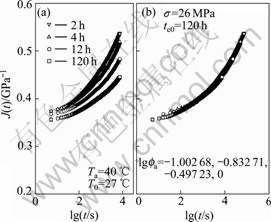
Fig.10 Creep compliance vs time at T_a=50 ℃, σ=26 MPa

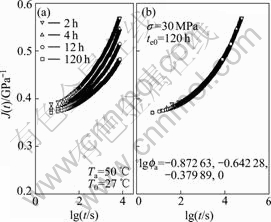
Fig.11 Creep compliance vs time at T_a=50 ℃, σ=30 MPa

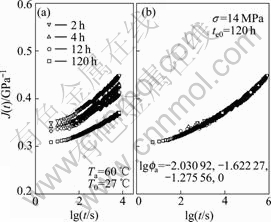
Fig.12 Creep compliance vs time at T_a=60 ℃, σ=14 MPa

The superposed master creep compliance curves at reference ageing time 120 h at stresses 14, 18, 22, 26 and 30 MPa in the case of ageing temperature 60 ℃ are individually shown in Fig.12(b) to Fig.16(b).

It can be found from these figures that the creep rate of PMMA increases with stress level increasing, but decreases with ageing time. In terms of the free volume theory, the free volume fraction in polymer decreases

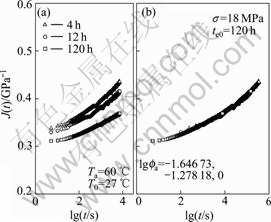
Fig.13 Creep compliance vs time at T_a=60 ℃, σ=18 MPa

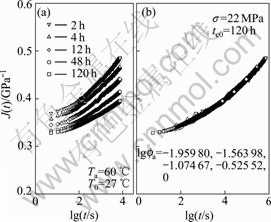
Fig.14 Creep compliance vs time at T_a=60 ℃, σ=22 MPa

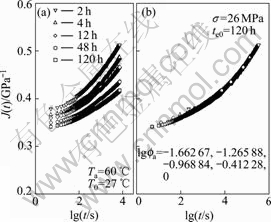
Fig.15 Creep compliance vs time at T_a=60 ℃, σ=26 MPa

with increasing ageing time, which results in descending activation energy in polymer and ascending polymeric material’s viscosity, so the creep speed is reversed with enhancing physical ageing. Consequently, the effect of decreasing ageing time or weakening intensity of physical ageing on the creep rate is equivalent to heightening environment temperature or stress level for polymers in service.

From the shifts  required to overlap the creep

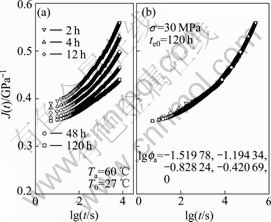
Fig.16 Creep compliance vs time at T_a=60 ℃, σ=30 MPa

curves at t_e, the amount of shift per decade of ageing time is obtained, that is, The ageing shift factor vs ageing time curves at ageing temperatures 40, 50 and 60 ℃ are individually given in Figs.17(a), (b) and (c). It is found that the ageing shift rate μ decreases with increasing stress, and remains constant over large time interval at each specified stress. Using this property, the shift factor of longer ageing time at a certain stress can be sought and the creep behavior can be forecast via reduced time, i.e. J(t, t_e)=J(ξ, t_e0),  ξ= The ageing shift rate at 14 MPa is almost equal at that at 18 MPa. For physical ageing of linear viscoelastic material, μ does not change with imposed stress. The results also show that the ageing time shift factors are dependent on the stresses at which the shifts are applied.

3.2 Time-stress equivalence

According to the theory of viscoelasticity, if the creep compliance is independent on the imposed stress, the material appears as linear viscoelasticity, otherwise appears as nonlinear one. It is found from Fig.18(a) to Fig.20(a) that there exists a critical stress within which the creep curves overlap one another and so the behavior is linear, and beyond which the creep curves depart from each other and so the behavior is nonlinear. The critical stress value of PMMA at room temperature is 18 MPa. This result agrees well with the aforementioned analysis on the ageing shift rate. Obviously, this critical value is independent on ageing temperature.

The time-stress equivalence states that the creep compliance at the loading time t with stress level σ is identical to that at time ξ with reference stress level σ^ref by setting  In the case of ageing temperature 40 ℃, the sub-master creep curves at 22, 26 and 30 MPa shown in Fig.4(b) to Fig.6(b) are horizontally shifted to the sub-master creep curve at 18 MPa shown in Fig.3(b) via stress shift factor, The master creep compliance

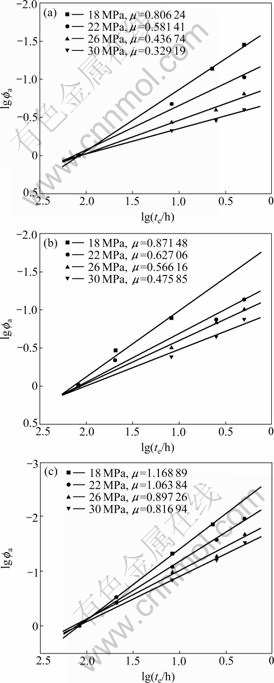
Fig.17 Ageing shift factor vs ageing time curves at (a) T_a=40 ℃; (b) T_a=50 ℃; (c) T_a=60 ℃

curve at reference ageing time 120 h and reference stress 18 MPa is plotted in Fig.18(b). Simultaneously, the sub-master creep curves at higher stress levels shown in Fig.9(b) to Fig.11(b) are shifted to that at lower stress level shown in Fig.8(b), and the master curve at reference state is built in Fig.19(b). Finally, in the case of ageing temperature 60 ℃, the sub-master curves given in Fig.13(b) to Fig.16(b) are superimposed into a master curve, as shown in Fig.20(b), via time shift along logarithmic time axis. From Figs.18, 19 and 20, it can be found that the stress changes the intrinsic timescale in polymer, and high stress level accelerates the process of creep and relaxation of polymer. Therefore, when the creep curves at higher stress levels shift to lower stress level, the constructed master creep curve spans a far more wider time frame than the tested creep curve does.

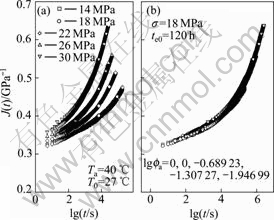
Fig.18 Master creep curves at T_a=40 ℃, t_e0=120 h, σ=18 MPa

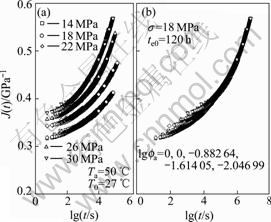
Fig.19 Master creep curve at T_a=50 ℃, t_e0=120 h, σ=18 MPa

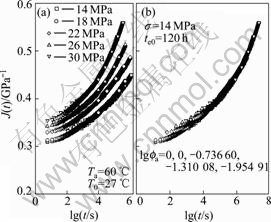
Fig.20 Master creep curve at T_a=60 ℃, t_e0=120 h, σ=18 MPa

3.3 Effect of ageing temperature on creep behavior

To investigate the effect of ageing temperature T_a on the creep behavior of polymer, the master creep curves shown in Figs.18(b), 19(b) and 20(b) are re-plotted into Fig.21(a). It is found that the creep rate decreases with increasing ageing temperature. Consequently, elevating ageing temperature results in strengthening the intensity of physical ageing, which demonstrates the mechanical mechanism why the polymer at a high temperature is easier to ageing. Finally, the master creep curves at T_a of 40 and 50 ℃ are shifted along logarithmic time axis via ageing temperature shift factor, The reference T_a is 60 ℃, and the unified master creep curve is shown in Fig.21(b). The result indicates an accelerated creep characterization of 3.8 decades beyond the test duration. The creep behavior covering 540 d is characterized.

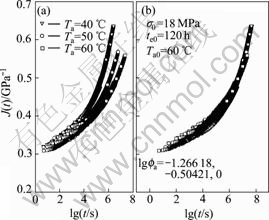
Fig.21 Unified master creep compliance curve at T_a0=60 ℃

1) The creep rate of PMMA increases with increasing stress level while decreases with ageing time. The time-stress equivalence, united with time-ageing time equivalence, provides an accelerated test technique in the laboratory.

2) For linear viscoelastic material, the ageing shift rate is independent on the imposed stress, but for non- linear one the ageing shift rate decreases with stress.

3) The analysis on creep strain and ageing shift rate demonstrate that for PMMA at room temperature, there exists a critical stress within which the creep behavior is linear and beyond which the creep behavior is nonlinear.

4) Elevating the ageing temperature results in the intensified physical ageing, so the creep rate is reversed with increasing ageing temperature.

[1] STRUIK l C e. Physical aging in amorphous polymers and other materials [M]. Amsterdam: Elsevier, 1978.

[2] HUTCHINSON J M. Physical aging of polymers [J]. Progress in Polymer Science, 1995, 20(4): 703-760.

[3] HUTCHINSON J M, SMITH S, HORNE B, GOURLAY G M. Physical aging of polycarbonate: enthalpy relaxation, creep response, and yielding behavior [J]. Macromolecules, 1999, 32(15): 5046-5061.

[4] TOMLINS P E, READ B E. Creep and physical ageing of polypropylene: A comparison of models [J]. Polymer, 1998, 39(2): 355-367.

[5] VLASVELD D P N, BERSEE H E N, PICKEN S J. Creep and physical aging behaviour of PA6 nanocomposites [J]. Polymer, 2005, 46(26): 12539-12545.

[6] ZHENG S F, WENG J G. A new constitutive equation for the long-term creep of polymers based on physical aging [J]. European Journal of Mechanics A/Solids, 2002, 21(3): 411-421.

[7] DEAN G D, TOMLINS P E, READ B E. A model for nonlinear creep and physical aging in poly(vinyl chloride) [J]. Polymer Engineering and Science, 1995, 35(16): 1282-1289.

[8] HO C H, VU-KHANH T. Effects of time and temperature on physical aging of polycarbonate [J]. Theoretical and Applied Fracture Mechanics, 2003, 39(2): 107-116.

[9] DROZDOV A D. Physical aging and nonlinear viscoelasticity of amorphous glassy polymer [J]. Computational Materials Science, 2001, 21(2): 197-213.

[10] KIM J, LEE W, TSAI S W. Modeling of mechanical property degradation by short-term aging at high temperatures [J]. Composites Part B: Engineering, 2002, 33(7): 531-543.

[11] WILLIAMS M L, LANDEL R F, FERRY J D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquid [J]. The Journal of the American Chemical Society, 1955, 77(14): 3701-3707.

[12] LUO Wen-bo, YANG Ting-qing, AN Qun-li. Time-temperature-stress equivalence and its application to nonlinear viscoelastic materials [J]. Acta Mechanica Solida Sinica, 2001, 14(3): 195-199.

[13] GUEDES R M, MORAIS J J L, MARQUES A T, CARDON A H. Prediction of long-term behaviour of composite materials [J]. Computers and Structures, 2000, 76(1/3): 183-194.

[14] LUO Wen-bo, WANG Chu-hong, ZHAO Rong-guo. Application of time-temperature-stress superposition principle to nonlinear creep of poly(methyl methacrylate) [J]. Key Engineering Materials, 2007, 340/341: 1091-1096.

[15] JAZOULI S, LUO W, BREMAND F, VU-KHANH T. Application of time-stress equivalence to nonlinear creep of polycarbonate [J]. Polymer Testing, 2005, 24(4): 463-467.

[16] JAZOULI S, LUO W, BREMAND F, VU-KHANH T. Nonlinear creep behavior of viscoelastic polycarbonate [J]. Journal of Materials Science, 2006, 41(2): 531-536.

[17] JONES D I G, FRENCH R M, BAGLEY R L. A renewal theory of small-strain thermo-mechanical response [J]. Mechanics of Materials, 1996, 23(2): 155-164.

[18] ZHAO Rong-guo, LUO Wen-bo, WANG Chu-hong, TANG Xin. Effect of stress-induced damage evolution on long-term creep behavior of nonlinear viscoelastic polymer [J]. Key Engineering Materials, 2006, 324/325: 731-734.

(Edited by YUAN Sai-qian)

Foundation item: Projects(10772156, 10672136) supported by the National Natural Science Foundation of China; Project(05C100) supported by the Scientific Research Fund of Education Department of Hunan Province, China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: ZHAO Rong-guo, Associated Professor; Tel: +86-732-8293214; E-mail: zhaorongguo@xtu.edu.cn